import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d.proj3d import proj_transform
from mpl_toolkits.mplot3d.axes3d import Axes3D
from matplotlib.text import Annotation
from matplotlib.patches import FancyArrowPatch
import matplotlib.patches as mpatches
class Annotation3D(Annotation):
def __init__(self, text, xyz, *args, **kwargs):
super().__init__(text, xy=(0,0), *args, **kwargs)
self._xyz = xyz
def draw(self, renderer):
x2, y2, z2 = proj_transform(*self._xyz, renderer.M)
self.xy=(x2,y2)
super().draw(renderer)
def _annotate3D(ax,text, xyz, *args, **kwargs):
'''Add anotation `text` to an `Axes3d` instance.'''
annotation= Annotation3D(text, xyz, *args, **kwargs)
ax.add_artist(annotation)
setattr(Axes3D,'annotate3D',_annotate3D)
class Arrow3D(FancyArrowPatch):
def __init__(self, x, y, z, dx, dy, dz, *args, **kwargs):
super().__init__((0,0), (0,0), *args, **kwargs)
self._xyz = (x,y,z)
self._dxdydz = (dx,dy,dz)
def draw(self, renderer):
x1,y1,z1 = self._xyz
dx,dy,dz = self._dxdydz
x2,y2,z2 = (x1+dx,y1+dy,z1+dz)
xs, ys, zs = proj_transform((x1,x2),(y1,y2),(z1,z2), renderer.M)
self.set_positions((xs[0],ys[0]),(xs[1],ys[1]))
super().draw(renderer)
def _arrow3D(ax, x, y, z, dx, dy, dz, *args, **kwargs):
'''Add an 3d arrow to an `Axes3D` instance.'''
arrow = Arrow3D(x, y, z, dx, dy, dz, *args, **kwargs)
ax.add_artist(arrow)
setattr(Axes3D,'arrow3D',_arrow3D)
jp_score = np.array([49, 58, 64, 65, 54, 58, 49, 67, 54, 66, 72, 66, 54, 64, 39,
56, 54, 56, 48, 57, 57, 47, 50, 60, 72, 54, 59, 61, 64, 70])
math_score = np.array([51, 58, 56, 70, 45, 70, 45, 69, 66, 73, 71, 72, 57, 53, 58,
57, 71, 63, 53, 62, 62, 59, 57, 65, 74, 66, 72, 50, 69, 60])
en_score = np.array([59, 63, 68, 77, 55, 71, 57, 79, 66, 81, 81, 77, 62, 67, 56,
62, 70, 67, 61, 70, 68, 59, 61, 71, 77, 66, 70, 59, 68, 71])
mean_vector = np.array([jp_score.mean(), math_score.mean(), en_score.mean()])
data_matrix = np.c_[jp_score, math_score, en_score]
data_mean_reduced = data_matrix - mean_vector
covariance_matrix = np.dot(data_mean_reduced.T, data_mean_reduced) / len(jp_score)
eigen_values, eigen_vectors = np.linalg.eig(covariance_matrix)
sorted_index = eigen_values.argsort()[::-1]
eigen_values=eigen_values[sorted_index]
eigen_vectors=eigen_vectors[:, sorted_index]
eigen_values, eigen_vectors = np.linalg.eig(covariance_matrix)
sorted_idx = eigen_values.argsort()[::-1]
eigen_values = eigen_values[sorted_idx]
eigen_vectors = eigen_vectors[:,sorted_idx]
eigen_vectors = eigen_vectors.astype(float)
subject_labels = ['Japanese score deviation', 'Math score deviation', 'English score deviation']
const_range = 2
X = np.arange(-const_range, const_range + 1, 1)
Y = np.arange(-const_range, const_range + 1, 1)
Z = np.arange(-const_range, const_range + 1, 1)
U_x, U_y, U_z = np.meshgrid(X, Y, Z)
V_x = np.zeros((len(U_x), len(U_y), len(U_z)))
V_y = np.zeros((len(U_x), len(U_y), len(U_z)))
V_z = np.zeros((len(U_x), len(U_y), len(U_z)))
temp_vec = np.zeros((1, 3))
W_x = np.zeros((len(U_x), len(U_y), len(U_z)))
W_y = np.zeros((len(U_x), len(U_y), len(U_z)))
W_z = np.zeros((len(U_x), len(U_y), len(U_z)))
fig = plt.figure(figsize=(15, 15))
grid_range = 15
for idx in range(2):
if idx ==0:
ax = fig.add_subplot(1, 2, idx + 1, projection='3d')
for i in range(len(U_x)):
for j in range(len(U_x)):
for k in range(len(U_x)):
temp_vec[0][0] = U_x[i][j][k]
temp_vec[0][1] = U_y[i][j][k]
temp_vec[0][2] = U_z[i][j][k]
temp_vec[0] = np.dot(covariance_matrix, temp_vec[0])
V_x[i][j][k] = temp_vec[0][0]
V_y[i][j][k] = temp_vec[0][1]
V_z[i][j][k] = temp_vec[0][2]
W_x[i][j][k] = (V_x[i][j][k] - U_x[i][j][k]) / (2*grid_range)
W_y[i][j][k] = (V_y[i][j][k] - U_y[i][j][k]) / (2*grid_range)
W_z[i][j][k] = (V_z[i][j][k] - U_z[i][j][k]) / (2*grid_range)
ax.arrow3D(0, 0, 0,
U_x[i][j][k], U_y[i][j][k], U_z[i][j][k],
mutation_scale=10, arrowstyle="-|>", fc='dimgrey', ec='dimgrey')
#ax.arrow3D(0, 0, 0,
# V_x[i][j][k], V_y[i][j][k], V_z[i][j][k],
# mutation_scale=10, arrowstyle="-|>", fc='red', ec='red')
ax.arrow3D(U_x[i][j][k], U_y[i][j][k], U_z[i][j][k],
W_x[i][j][k], W_y[i][j][k], W_z[i][j][k],
mutation_scale=10, arrowstyle="-|>", fc='darkviolet', ec='darkviolet')
if idx==1:
ax = fig.add_subplot(1, 2, idx + 1, projection='3d')
ax.scatter(data_mean_reduced[:, 0], data_mean_reduced[:, 1], data_mean_reduced[:, 2], marker='o', s=80)
ax.arrow3D(0, 0, 0, eigen_vectors.T[0][0]*10, eigen_vectors.T[0][1]*10, eigen_vectors.T[0][2]*10,
mutation_scale=10, arrowstyle="-|>", fc='orange', ec='orange', lw = 3)
ax.arrow3D(0, 0, 0, eigen_vectors.T[1][0]*10, eigen_vectors.T[1][1]*10, eigen_vectors.T[1][2]*10,
mutation_scale=10, arrowstyle="-|>", fc='orange', ec='orange', lw = 3)
ax.arrow3D(0, 0, 0, eigen_vectors.T[2][0]*10, eigen_vectors.T[2][1]*10, eigen_vectors.T[2][2]*10,
mutation_scale=10, arrowstyle="-|>", fc='orange', ec='orange', lw = 3)
ax.text(eigen_vectors.T[0][0]*8 , eigen_vectors.T[0][1]*8, eigen_vectors.T[0][2]*8+1, r'$u_1$', fontsize=20)
ax.text(eigen_vectors.T[1][0]*8 , eigen_vectors.T[1][1]*8, eigen_vectors.T[1][2]*8, r'$u_2$', fontsize=20)
ax.text(eigen_vectors.T[2][0]*8 , eigen_vectors.T[2][1]*8, eigen_vectors.T[2][2]*8, r'$u_3$', fontsize=20)
ax.set_xlim(-grid_range, grid_range)
ax.set_ylim(-grid_range, grid_range)
ax.set_zlim(-grid_range, grid_range)
#ax.set_xlabel(r'$x_1$', fontsize=25)
#ax.set_ylabel(r'$x_2$', fontsize=25)
#ax.set_zlabel(r'$x_3$', fontsize=25)
ax.set_xlabel(subject_labels[0], fontsize=10)
ax.set_ylabel(subject_labels[1], fontsize=10)
ax.set_zlabel(subject_labels[2], fontsize=10)
#lt.savefig("visualizing_covariance_matrix.png")
plt.show()


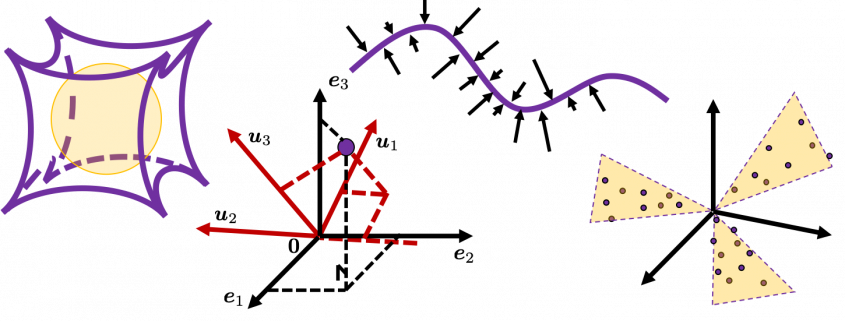




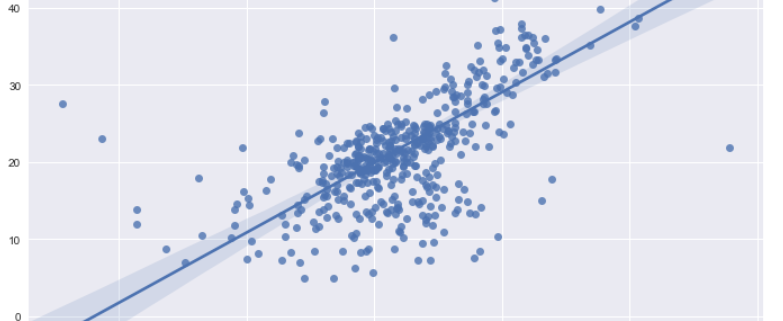
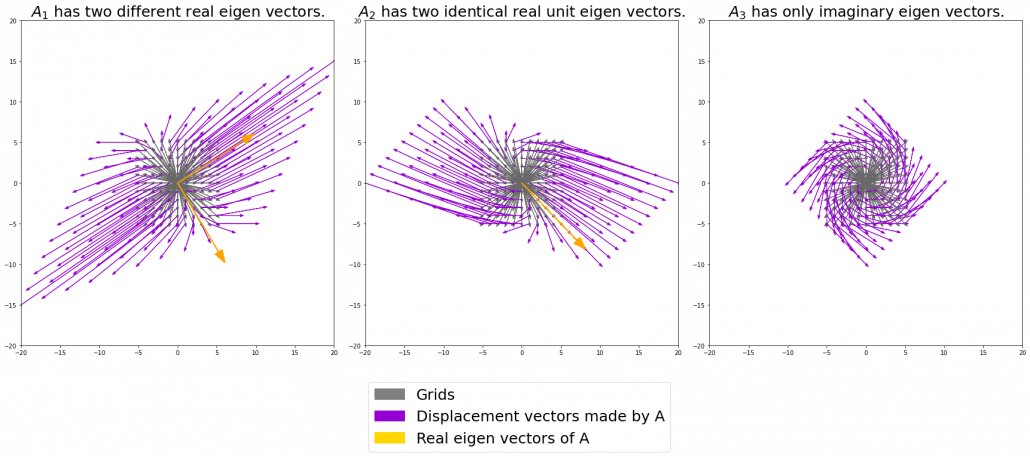
 , and in fact the matrix is just a constant multiplication of this covariance matrix. I think now you understand that PCA is calculating the orthogonal eigenvectors of covariance matrix of data, that is diagonalizing covariance matrix with orthonormal eigenvectors. Hence we can guess that covariance matrix enables a type of linear transformation of rotation and expansion and contraction of vectors. And data points swell along eigenvectors of such matrix.
, and in fact the matrix is just a constant multiplication of this covariance matrix. I think now you understand that PCA is calculating the orthogonal eigenvectors of covariance matrix of data, that is diagonalizing covariance matrix with orthonormal eigenvectors. Hence we can guess that covariance matrix enables a type of linear transformation of rotation and expansion and contraction of vectors. And data points swell along eigenvectors of such matrix.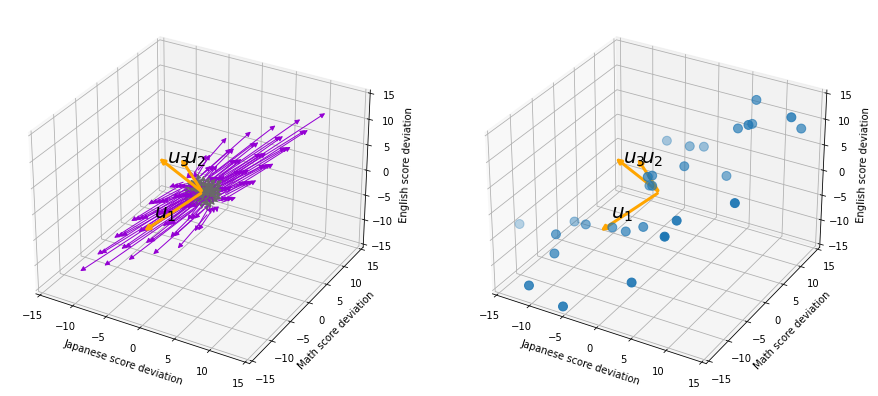
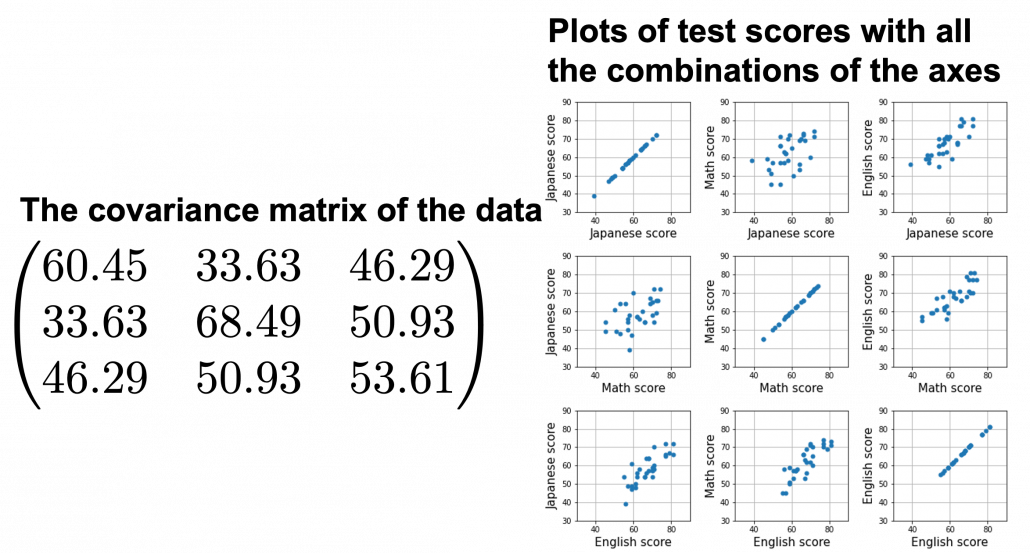
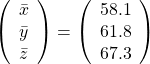 , and the covariance matrix of data in the original coordinate system is
, and the covariance matrix of data in the original coordinate system is  . The eigenvalues of
. The eigenvalues of 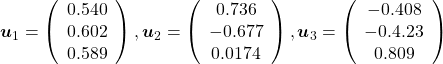 respectively.
respectively. 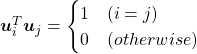 . As I explained in the last article, you can diagonalize
. As I explained in the last article, you can diagonalize 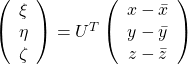 .
.
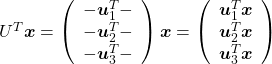 , and
, and 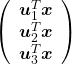 denotes the coordinate point of the purple point in the red coordinate system.
denotes the coordinate point of the purple point in the red coordinate system. 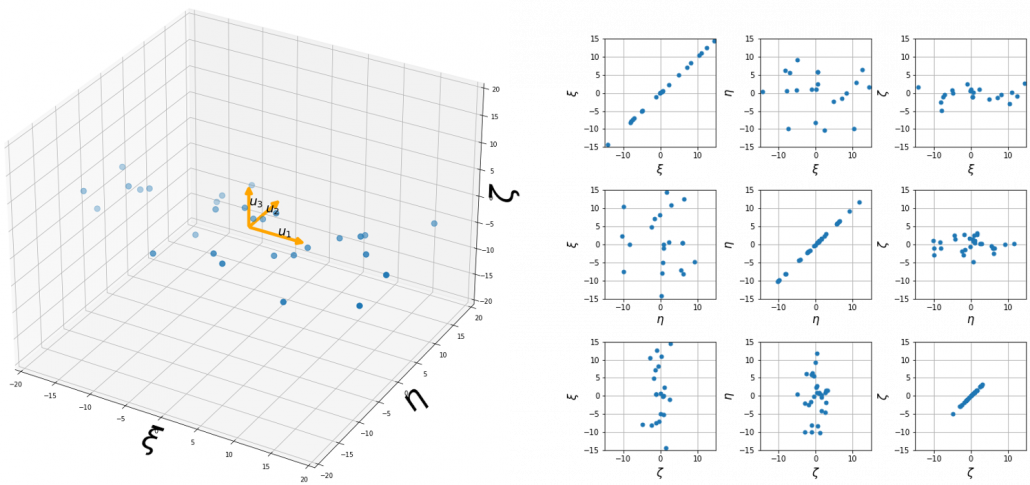
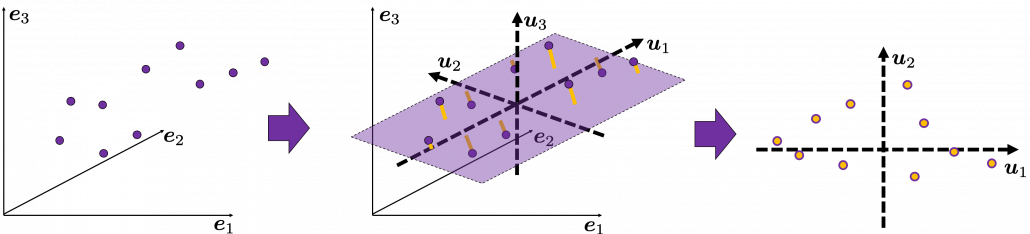
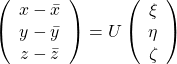 , which means you can express deviations of the original data as linear combinations of the three factors
, which means you can express deviations of the original data as linear combinations of the three factors  . You can see
. You can see 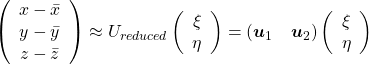 . Then it mathematically clearer that we can express the data with two factors: “how smart the student is” and “whether he is at scientific side or liberal art side.”
. Then it mathematically clearer that we can express the data with two factors: “how smart the student is” and “whether he is at scientific side or liberal art side.”



 .
. Most textbooks keep explaining these type of stuff, but I have to say they lack efforts to make it understandable to readers with low mathematical literacy like me. Especially if you have to apply the idea to data science field, I believe you need more visual understanding of diagonalization. Therefore instead of just explaining the definitions and theorems, I would like to take a different approach. But in order to understand them in more intuitive ways, we first have to rethink waht linear transformation
Most textbooks keep explaining these type of stuff, but I have to say they lack efforts to make it understandable to readers with low mathematical literacy like me. Especially if you have to apply the idea to data science field, I believe you need more visual understanding of diagonalization. Therefore instead of just explaining the definitions and theorems, I would like to take a different approach. But in order to understand them in more intuitive ways, we first have to rethink waht linear transformation  *I am not going to use the term “linear transformation” in a precise way in the context of linear algebra. In this article or in the context of data science or machine learning, “linear transformation” for the most part means products of matrices or vectors.
*I am not going to use the term “linear transformation” in a precise way in the context of linear algebra. In this article or in the context of data science or machine learning, “linear transformation” for the most part means products of matrices or vectors.  Let’s calculate the displacement vector with more vectors
Let’s calculate the displacement vector with more vectors 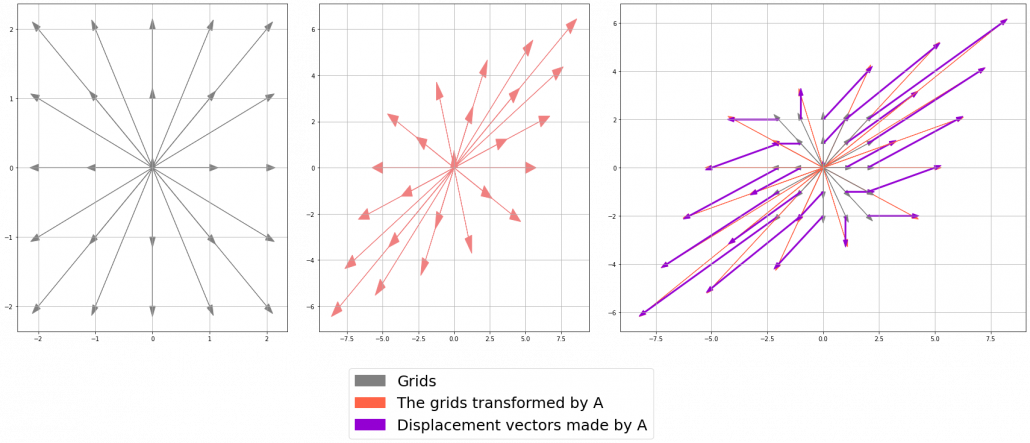

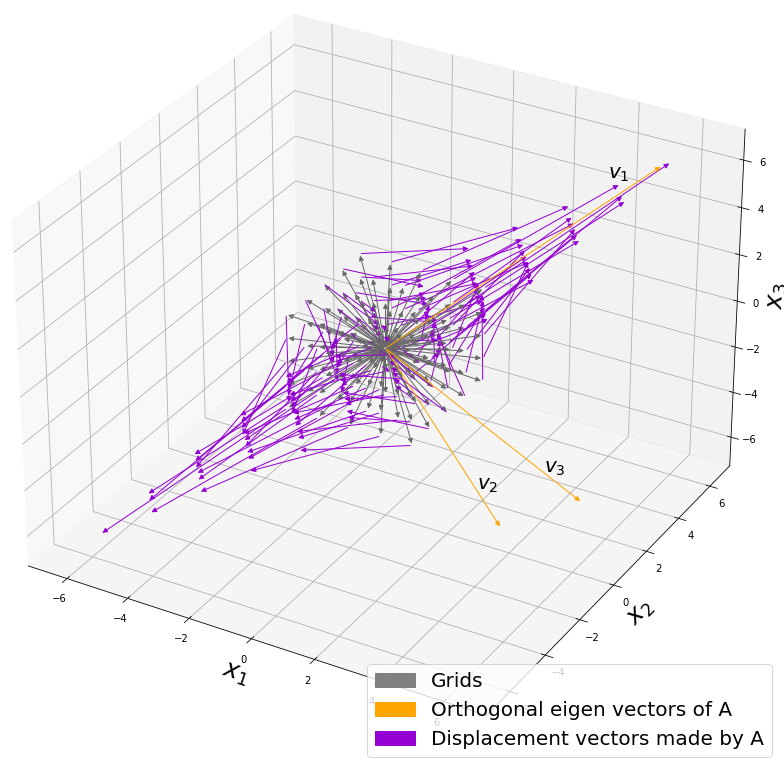
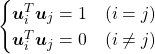 . In other words column vectors
. In other words column vectors  ,
, 
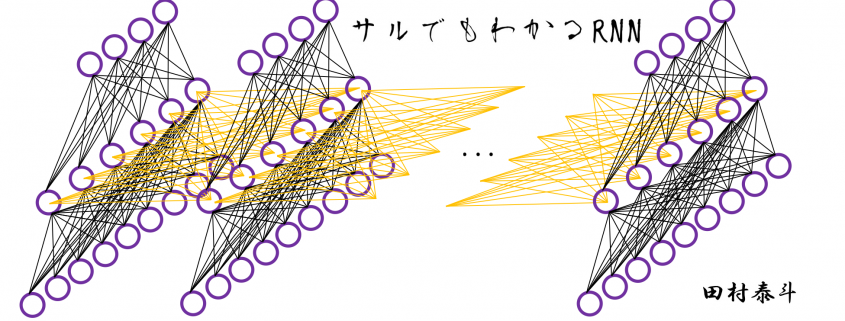

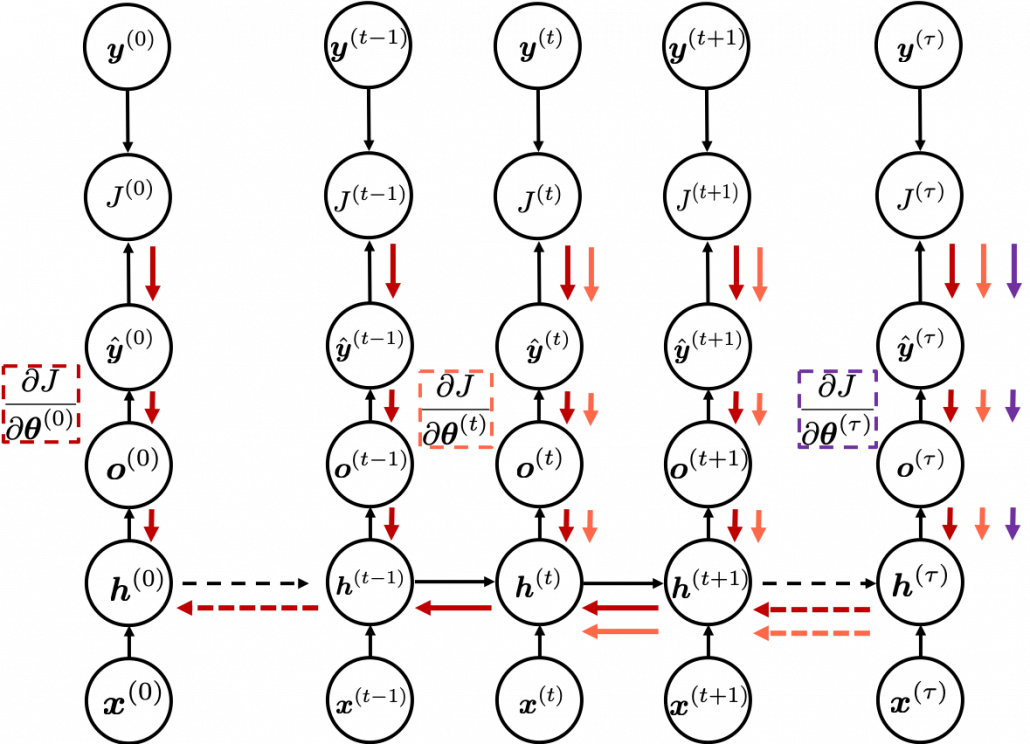
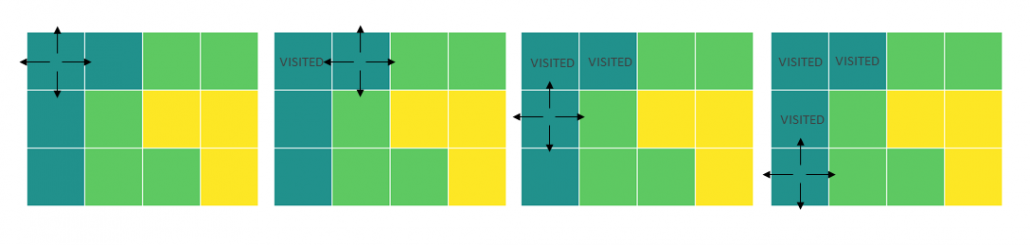
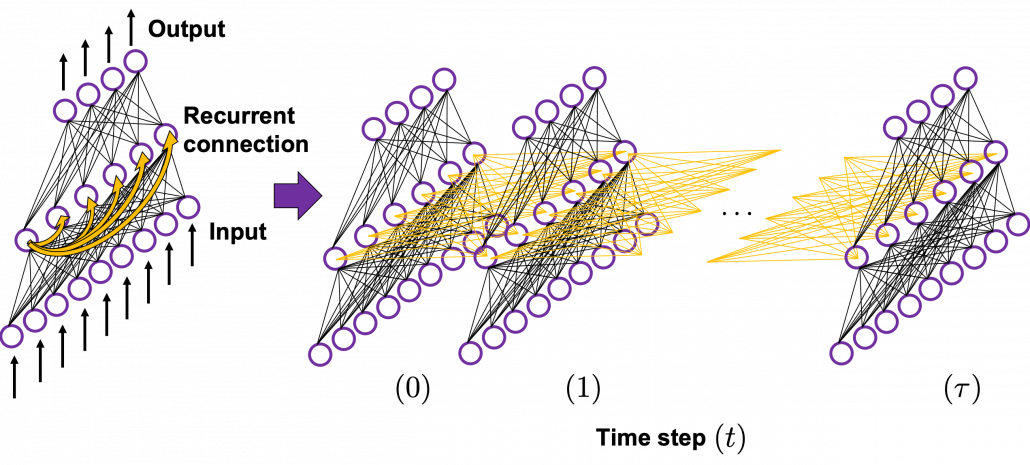
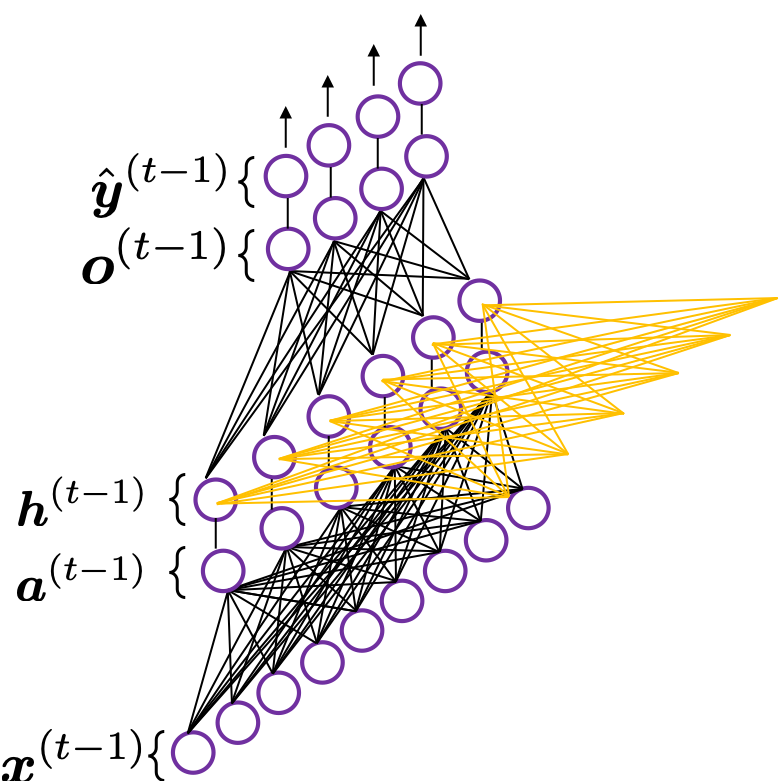
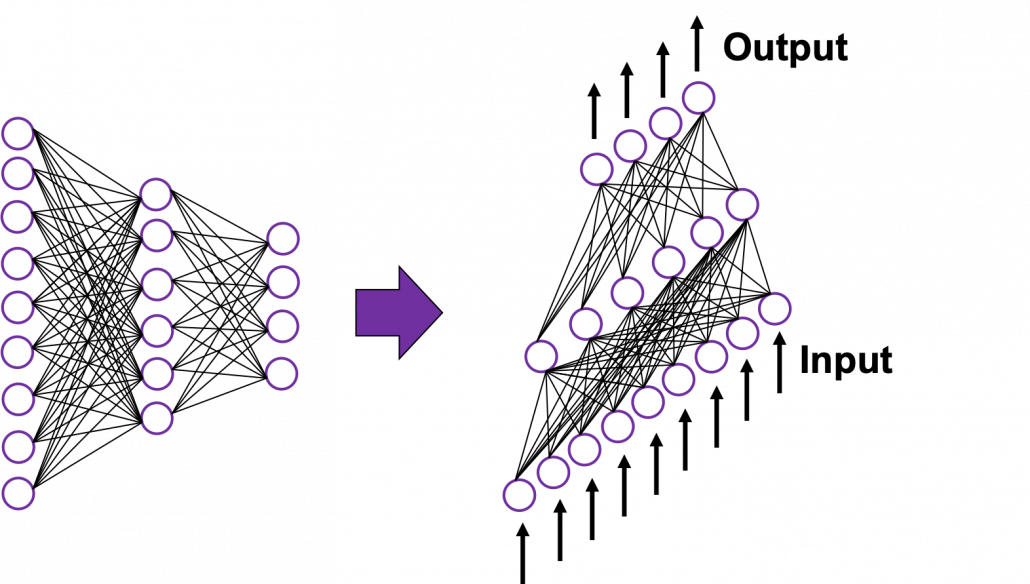 In fact the simple RNN which we are going to look at in this article has only three layers. From now on imagine that inputs of RNN come from the bottom and outputs go up. But RNNs have to keep information of earlier times steps during upcoming several time steps because as I mentioned in the last article RNNs are used for sequence data, the order of whose elements is important. In order to do that, information of the neurons in the middle layer of RNN propagate forward to the middle layer itself. Therefore in one time step of forward propagation of RNN, the input at the time step propagates forward as normal DCL, and the RNN gives out an output at the time step. And information of one neuron in the middle layer propagate forward to the other neurons like yellow arrows in the figure. And the information in the next neuron propagate forward to the other neurons, and this process is repeated. This is called recurrent connections of RNN.
In fact the simple RNN which we are going to look at in this article has only three layers. From now on imagine that inputs of RNN come from the bottom and outputs go up. But RNNs have to keep information of earlier times steps during upcoming several time steps because as I mentioned in the last article RNNs are used for sequence data, the order of whose elements is important. In order to do that, information of the neurons in the middle layer of RNN propagate forward to the middle layer itself. Therefore in one time step of forward propagation of RNN, the input at the time step propagates forward as normal DCL, and the RNN gives out an output at the time step. And information of one neuron in the middle layer propagate forward to the other neurons like yellow arrows in the figure. And the information in the next neuron propagate forward to the other neurons, and this process is repeated. This is called recurrent connections of RNN.
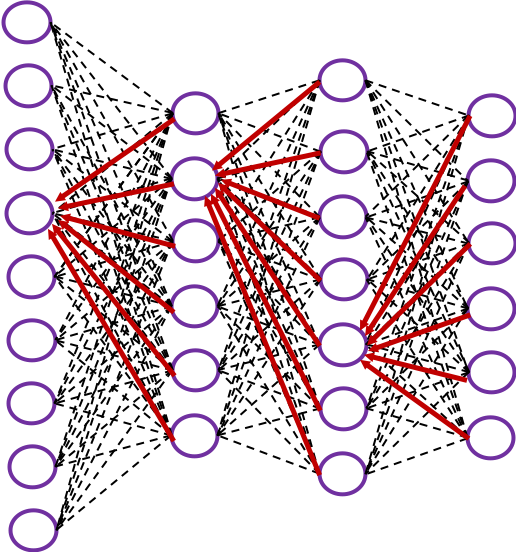
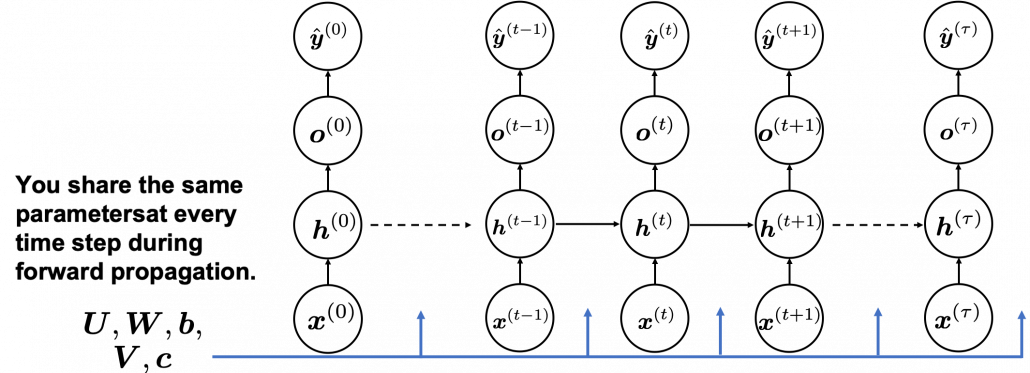
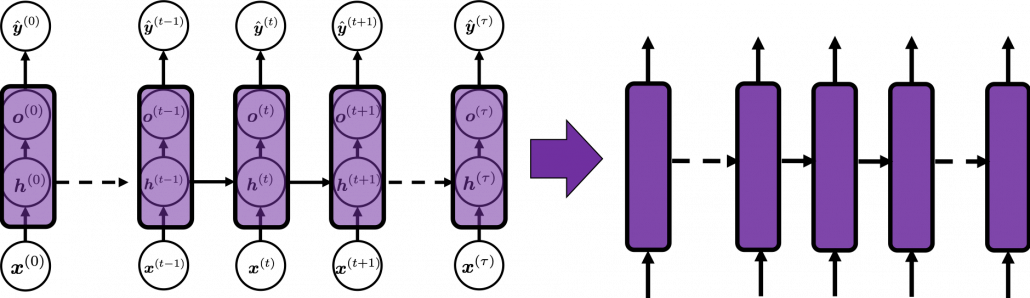
 In many situations, RNNs are simplified as below. If you have read through this article until this point, I bet you gained some better understanding of RNNs, so you should little by little get used to this more abstract, blackboxed way of showing RNN.
In many situations, RNNs are simplified as below. If you have read through this article until this point, I bet you gained some better understanding of RNNs, so you should little by little get used to this more abstract, blackboxed way of showing RNN.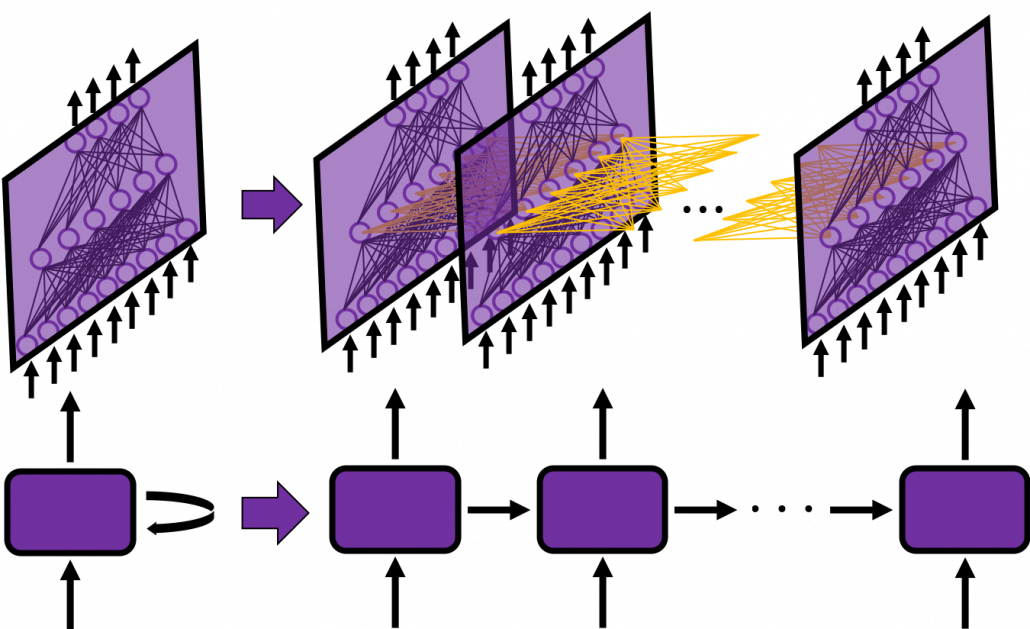
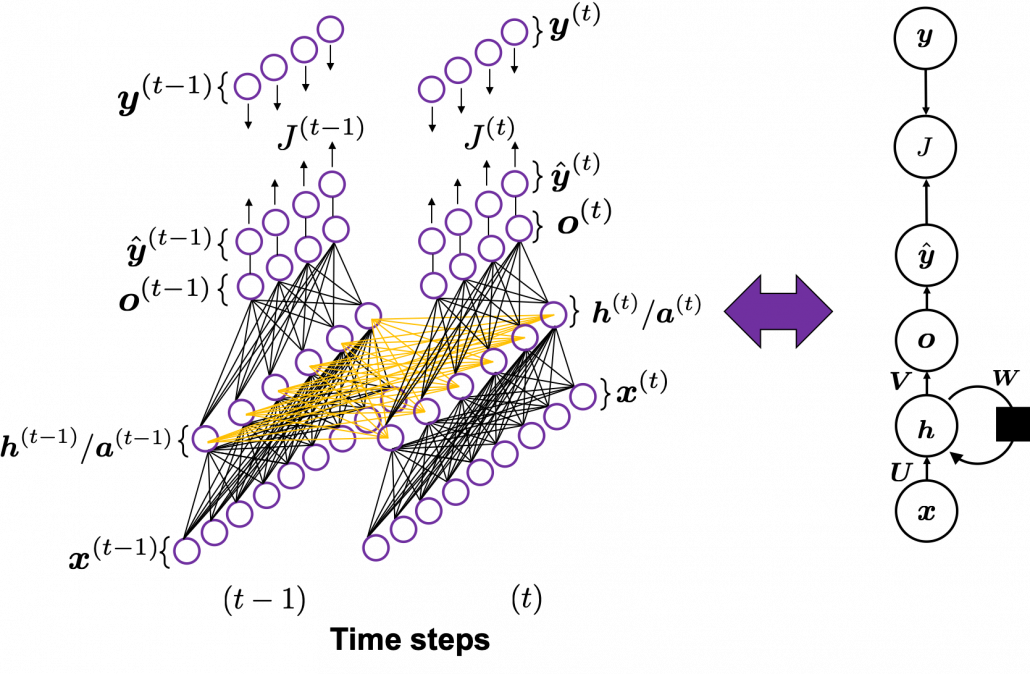

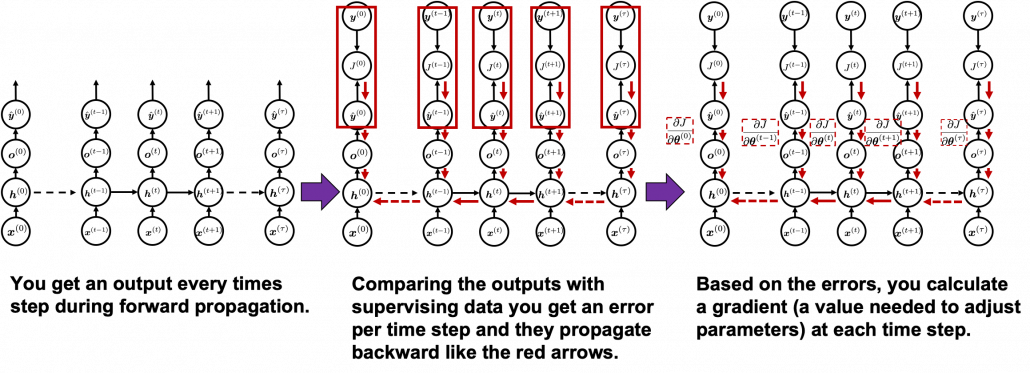 You need all the gradients to adjust parameters, but you do not necessarily need all the errors to calculate those gradients. Gradients in the context of machine learning mean partial derivatives of error functions (in this case
You need all the gradients to adjust parameters, but you do not necessarily need all the errors to calculate those gradients. Gradients in the context of machine learning mean partial derivatives of error functions (in this case