Rethinking linear algebra: visualizing linear transformations and eigenvectors
In terms of calculation processes of Principal Component Analysis (PCA) or Linear Discriminant Analysis (LDA), which are the dimension reduction techniques I am going to explain in the following articles, diagonalization is what they are all about. Throughout this article, I would like you to have richer insight into diagonalization in order to prepare for understanding those basic dimension reduction techniques.
When our professor started a lecture on the last chapter of our textbook on linear algebra, he said “It is no exaggeration to say that everything we have studied is for this ‘diagonalization.'” Until then we had to write tons of numerical matrices and vectors all over our notebooks, calculating those products, adding their rows or columns to other rows or columns, sometimes transposing the matrices, calculating their determinants.
It was like the scene in “The Karate Kid,” where the protagonist finally understood the profound meaning behind the prolonged and boring “wax on, wax off” training given by Miyagi (or “jacket on, jacket off” training given by Jackie Chan). We had finally understood why we had been doing those seemingly endless calculations.

Source: http://thinkbedoleadership.com/secret-success-wax-wax-off/
But usually you can do those calculations easily with functions in the Numpy library. Unlike Japanese college freshmen, I bet you are too busy to reopen textbooks on linear algebra to refresh your mathematics. Thus I am going to provide less mathematical and more intuitive explanation of diagonalization in this article.
*This is the second article of the article series ” Illustrative introductions on dimension reduction .”
1, The mainstream ways of explaining diagonalization.
*The statements below are very rough for mathematical topics, but I am going to give priority to offering more visual understanding on linear algebra in this article. For further understanding, please refer to textbooks on linear algebra. If you would like to have minimum understandings on linear algebra needed for machine learning, I recommend the Appendix C of Pattern Recognition and Machine Learning by C. M. Bishop.
In most textbooks on linear algebra, the explanations on dioagonalization is like this (if you are not sure what diagonalization is or if you are allergic to mathematics, you do not have to read this seriously):
Let ![]() be a vector space and let
be a vector space and let ![]() be a mapping of
be a mapping of ![]() into itself, defined as
into itself, defined as ![]() , where
, where ![]() is a
is a ![]() matrix and
matrix and ![]() is
is ![]() dimensional vector. An element
dimensional vector. An element ![]() is called an eigen vector if there exists a number
is called an eigen vector if there exists a number ![]() such that
such that ![]() and
and ![]() . In this case
. In this case ![]() is uniquely determined and is called an eigen value of
is uniquely determined and is called an eigen value of ![]() belonging to the eigen vector
belonging to the eigen vector ![]() .
.
Any matrix ![]() has
has ![]() eigen values
eigen values ![]() , belonging to
, belonging to ![]() . If
. If ![]() is basis of the vector space
is basis of the vector space ![]() , then
, then ![]() is diagonalizable.
is diagonalizable.
When ![]() is diagonalizable, with
is diagonalizable, with ![]() matrices
matrices ![]() , whose column vectors are eigen vectors
, whose column vectors are eigen vectors ![]() , the following equation holds:
, the following equation holds: ![]() , where
, where 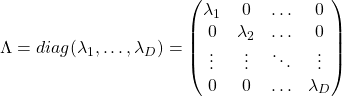 .
.
And when ![]() is diagonalizable, you can diagonalize
is diagonalizable, you can diagonalize ![]() as below.
as below.
 Most textbooks keep explaining these type of stuff, but I have to say they lack efforts to make it understandable to readers with low mathematical literacy like me. Especially if you have to apply the idea to data science field, I believe you need more visual understanding of diagonalization. Therefore instead of just explaining the definitions and theorems, I would like to take a different approach. But in order to understand them in more intuitive ways, we first have to rethink waht linear transformation
Most textbooks keep explaining these type of stuff, but I have to say they lack efforts to make it understandable to readers with low mathematical literacy like me. Especially if you have to apply the idea to data science field, I believe you need more visual understanding of diagonalization. Therefore instead of just explaining the definitions and theorems, I would like to take a different approach. But in order to understand them in more intuitive ways, we first have to rethink waht linear transformation ![]() means in more visible ways.
means in more visible ways.
2, Linear transformations
Even though I did my best to make this article understandable to people with little prerequisite knowledge, you at least have to understand linear transformation of numerical vectors and with matrices. Linear transformation is nothing difficult, and in this article I am going to use only 2 or 3 dimensional numerical vectors or square matrices. You can calculate linear transformation of ![]() by
by ![]() as equations in the figure. In other words,
as equations in the figure. In other words, ![]() is a vector transformed by
is a vector transformed by ![]() .
.
 *I am not going to use the term “linear transformation” in a precise way in the context of linear algebra. In this article or in the context of data science or machine learning, “linear transformation” for the most part means products of matrices or vectors.
*I am not going to use the term “linear transformation” in a precise way in the context of linear algebra. In this article or in the context of data science or machine learning, “linear transformation” for the most part means products of matrices or vectors.
*Forward/back propagation of deep learning is mainly composed of this linear transformation. You keep linearly transforming input vectors, frequently transforming them with activation functions, which are for the most part not linear transformation.
As you can see in the equations above, linear transformation with ![]() transforms a vector to another vector. Assume that you have an original vector
transforms a vector to another vector. Assume that you have an original vector ![]() in grey and that the vector
in grey and that the vector ![]() in pink is the transformed
in pink is the transformed ![]() by
by ![]() is. If you subtract
is. If you subtract ![]() from
from ![]() , you can get a displacement vector, which I displayed in purple. A displacement vector means the transition from a vector to another vector.
, you can get a displacement vector, which I displayed in purple. A displacement vector means the transition from a vector to another vector.
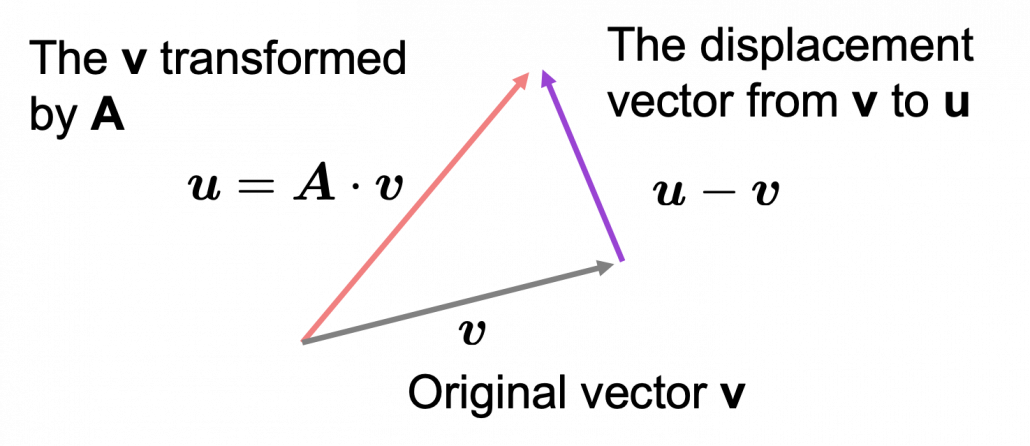 Let’s calculate the displacement vector with more vectors
Let’s calculate the displacement vector with more vectors ![]() . Assume that
. Assume that ![]() , and I prepared several grid vectors
, and I prepared several grid vectors ![]() in grey as you can see in the figure below. If you transform those grey grid points with
in grey as you can see in the figure below. If you transform those grey grid points with ![]() , they are mapped into the vectors
, they are mapped into the vectors ![]() in pink. With those vectors in grey or pink, you can calculate the their displacement vectors
in pink. With those vectors in grey or pink, you can calculate the their displacement vectors ![]() , which are in purple.
, which are in purple.
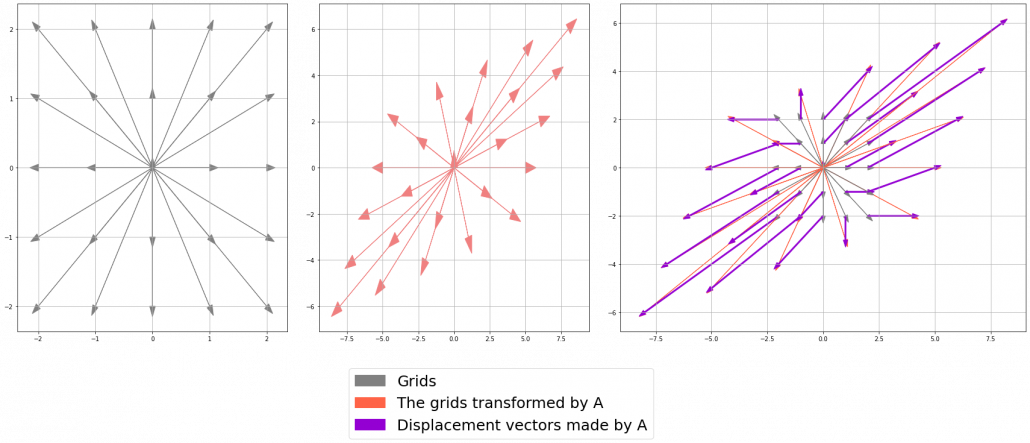
The displacement vectors in the figure above have some tendencies. In order to see that more clearly, let’s calculate displacement vectors with several matrices ![]() and more grid points. Assume that you have three
and more grid points. Assume that you have three ![]() square matrices
square matrices ![]() , and I plotted displace vectors made by the matrices respectively in the figure below.
, and I plotted displace vectors made by the matrices respectively in the figure below.
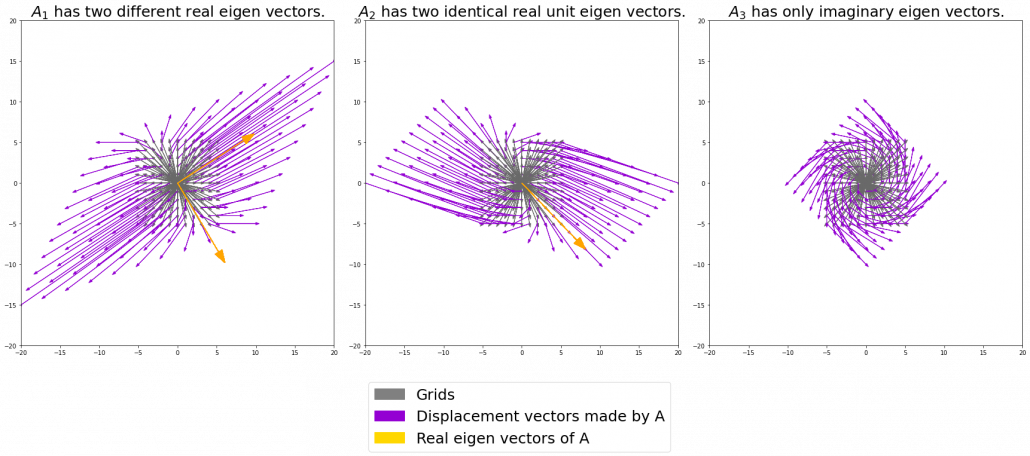
I think you noticed some characteristics of the displacement vectors made by those linear transformations: the vectors are swirling and many of them seem to be oriented in certain directions. To be exact, some displacement vectors extend in the same directions as some of original vectors in grey. That means linear transformation by ![]() did not change the direction of the original vector
did not change the direction of the original vector ![]() , and the unchanged vectors are called eigen vectors. Real eigen vectors of each A are displayed as arrows in yellow in the figure above. But when it comes to
, and the unchanged vectors are called eigen vectors. Real eigen vectors of each A are displayed as arrows in yellow in the figure above. But when it comes to ![]() , the matrix does not have any real eigan values.
, the matrix does not have any real eigan values.
In linear algebra, depending on the type matrices ![]() , you have to consider various cases such as whether the matrices have real or imaginary eigen values, whether the matrices are diagonalizable, whether the eigen vectors are orthogonal, or whether they are unit vectors. But those topics are out of the scope of this article series, so please refer to textbooks on linear algebra if you are interested.
, you have to consider various cases such as whether the matrices have real or imaginary eigen values, whether the matrices are diagonalizable, whether the eigen vectors are orthogonal, or whether they are unit vectors. But those topics are out of the scope of this article series, so please refer to textbooks on linear algebra if you are interested.
Luckily, however, in terms of PCA or LDA, you only have to consider a type of matrices named positive semidefinite matrices, which ![]() is classified to, and I am going to explain positive semidefinite matrices in the fourth section.
is classified to, and I am going to explain positive semidefinite matrices in the fourth section.
3, Eigen vectors as coordinate system
Source: Ian Stewart, “Professor Stewart’s Cabinet of Mathematical Curiosities,” (2008), Basic Books
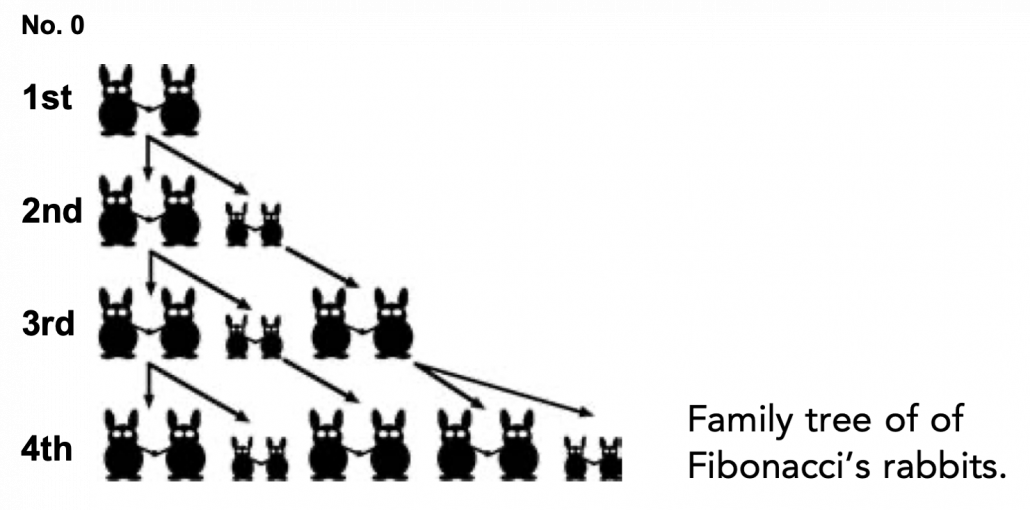
Let me take Fibonacci numbers as an example to briefly see why diagonalization is useful. Fibonacci is sequence is quite simple and it is often explained using an example of pairs of rabbits increasing generation by generation. Let ![]() be the number of pairs of grown up rabbits in the
be the number of pairs of grown up rabbits in the ![]() generation. One pair of grown up rabbits produce one pair of young rabbit The concrete values of
generation. One pair of grown up rabbits produce one pair of young rabbit The concrete values of ![]() are
are ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Assume that
. Assume that ![]() and that
and that ![]() , then you can calculate the number of the pairs of grown up rabbits in the next generation with the following recurrence relation.
, then you can calculate the number of the pairs of grown up rabbits in the next generation with the following recurrence relation. ![]() .Let
.Let ![]() be
be ![]() , then the recurrence relation can be written as
, then the recurrence relation can be written as ![]() , and the transition of
, and the transition of ![]() are like purple arrows in the figure below. It seems that the changes of the purple arrows are irregular if you look at the plots in normal coordinate.
are like purple arrows in the figure below. It seems that the changes of the purple arrows are irregular if you look at the plots in normal coordinate.
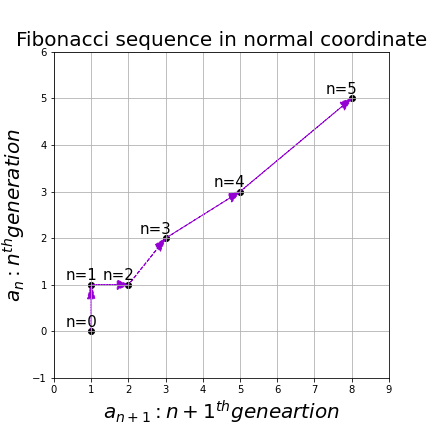
Assume that ![]() are eigen values of
are eigen values of ![]() , and
, and ![]() are eigen vectors belonging to them respectively. Also let
are eigen vectors belonging to them respectively. Also let ![]() scalars such that
scalars such that ![]() . According to the definition of eigen values and eigen vectors belonging to them, the following two equations hold:
. According to the definition of eigen values and eigen vectors belonging to them, the following two equations hold: ![]() . If you calculate
. If you calculate ![]() is, using eigen vectors of
is, using eigen vectors of ![]() ,
, ![]() . In the same way,
. In the same way, ![]() , and
, and ![]() . These equations show that in coordinate system made by eigen vectors of
. These equations show that in coordinate system made by eigen vectors of ![]() , linear transformation by
, linear transformation by ![]() is easily done by just multiplying eigen values with each eigen vector. Compared to the graph of Fibonacci numbers above, in the figure below you can see that in coordinate system made by eigen vectors the plots changes more systematically generation by generation.
is easily done by just multiplying eigen values with each eigen vector. Compared to the graph of Fibonacci numbers above, in the figure below you can see that in coordinate system made by eigen vectors the plots changes more systematically generation by generation.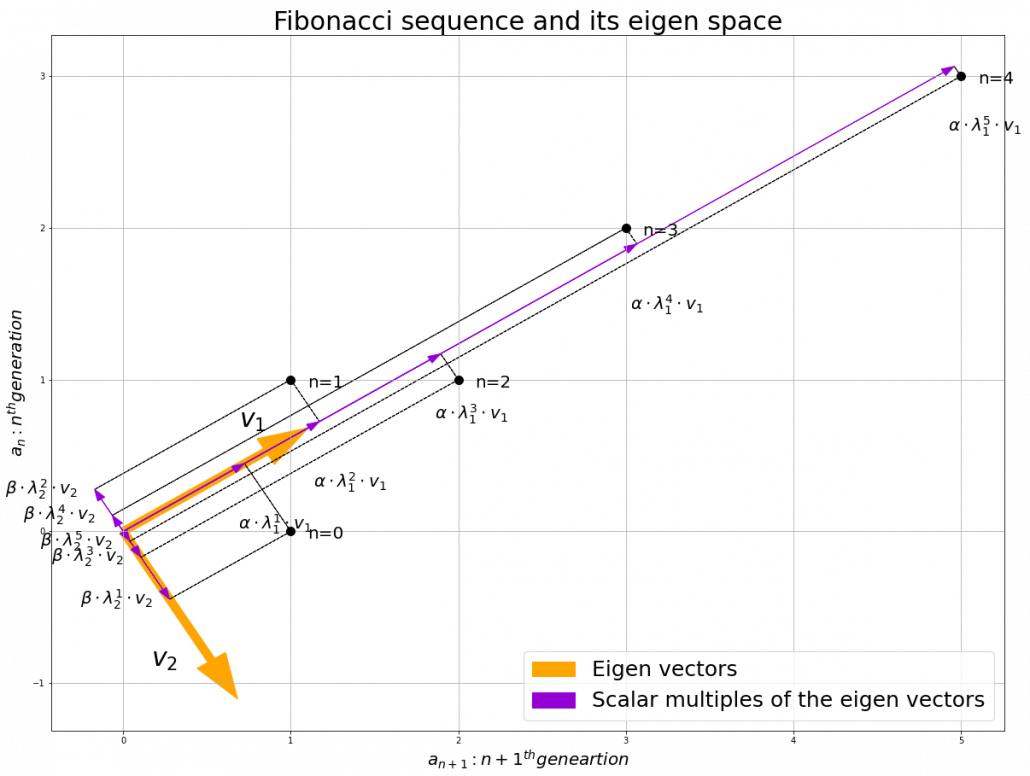
In coordinate system made by eigen vectors of square matrices, the linear transformations by the matrices can be much more straightforward, and this is one powerful strength of eigen vectors.
*I do not major in mathematics, so I am not 100% sure, but vectors in linear algebra have more abstract meanings. Various things in mathematics can be vectors, even though in machine learning or data science we mainly use numerical vectors with more concrete elements. We can also say that matrices are a kind of maps. That is just like, at least in my impression, even though a real town is composed of various components such as houses, smooth or bumpy roads, you can simplify its structure with simple orthogonal lines, like the map of Manhattan. But if you know what the town actually looks like, you do not have to follow the zigzag path on the map.
4, Eigen vectors of positive semidefinite matrices
In the second section of this article I told you that, even though you have to consider various elements when you discuss general diagonalization, in terms of PCA and LDA we mainly use only a type of matrices named positive semidefinite matrices. Let ![]() be a
be a ![]() square matrix. If
square matrix. If ![]() for all values of the vector
for all values of the vector ![]() , the
, the ![]() is said to be a positive semidefinite matrix. And also it is known that
is said to be a positive semidefinite matrix. And also it is known that ![]() being a semidefinite matrix is equivalent to
being a semidefinite matrix is equivalent to ![]() for all the eigen values
for all the eigen values ![]() .
.
*I think most people first learn a type of matrices called positive definite matrices. Let ![]() be a
be a![]() square matrix. If
square matrix. If ![]() for all values of the vector
for all values of the vector ![]() , the
, the ![]() is said to be a positive definite matrix. You have to keep it in mind that even if all the elements of
is said to be a positive definite matrix. You have to keep it in mind that even if all the elements of ![]() are positive,
are positive, ![]() is not necessarly positive definite/semidefinite.
is not necessarly positive definite/semidefinite.
Just as we did in the second section of this article, let’s visualize displacement vectors made by linear transformation with a ![]() square positive semidefinite matrix
square positive semidefinite matrix ![]() .
.
*In fact ![]() , whose linear transformation I visualized the second section, is also positive semidefinite.
, whose linear transformation I visualized the second section, is also positive semidefinite.
Let’s visualize linear transformations by a positive definite matrix  . I visualized the displacement vectors made by the
. I visualized the displacement vectors made by the ![]() just as the same way as in the second section of this article. The result is as below, and you can see that, as well as the displacement vectors made by
just as the same way as in the second section of this article. The result is as below, and you can see that, as well as the displacement vectors made by ![]() , the three dimensional displacement vectors below are swirling and extending in three directions, in the directions of the three orthogonal eigen vectors
, the three dimensional displacement vectors below are swirling and extending in three directions, in the directions of the three orthogonal eigen vectors ![]() , and
, and ![]() .
.
*It might seem like a weird choice of a matrix, but you are going to see why I chose it in the next article.
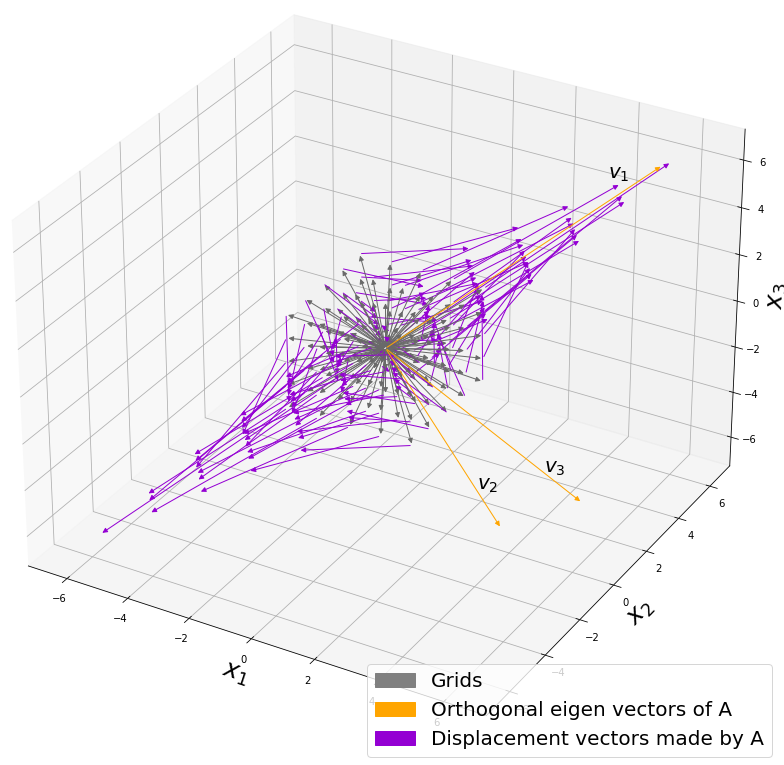
You might have already noticed ![]() and
and  are both symmetric matrices and that their elements are all real values, and that their diagonal elements are all positive values. Super importantly, when all the elements of a
are both symmetric matrices and that their elements are all real values, and that their diagonal elements are all positive values. Super importantly, when all the elements of a ![]() symmetric matrix
symmetric matrix ![]() are real values and its eigen values are
are real values and its eigen values are ![]() , there exist orthonormal matrices
, there exist orthonormal matrices ![]() such that
such that ![]() , where
, where ![]() .
.
*The title of this section might be misleading, but please keep it in mind that positive definite/semidefinite matrices are not necessarily real symmetric matrices. And real symmetric vectors are not necessarily positive definite/semidefinite matrices.
5, Orthonormal matrices and rotation of vectors
In this section I am gong to explain orthonormal matrices, as known as rotation matrices. If a ![]() matrix
matrix ![]() is an orthonormal matrix, column vectors of
is an orthonormal matrix, column vectors of ![]() are orthonormal, which means
are orthonormal, which means ![]() , where
, where 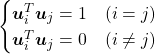 . In other words column vectors
. In other words column vectors ![]() form an orthonormal coordinate system.
form an orthonormal coordinate system.
Orthonormal matrices ![]() have several important properties, and one of the most important properties is
have several important properties, and one of the most important properties is ![]() . Combining this fact with what I have told you so far, you we can reach one conclusion: you can orthogonalize a real symmetric matrix
. Combining this fact with what I have told you so far, you we can reach one conclusion: you can orthogonalize a real symmetric matrix ![]() as
as ![]() . This is known as spectral decomposition or singular value decomposition.
. This is known as spectral decomposition or singular value decomposition.
Another important property of ![]() is that
is that ![]() is also orthonormal. In other words, assume
is also orthonormal. In other words, assume ![]() is orthonormal and that
is orthonormal and that 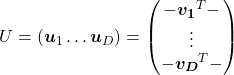 ,
, ![]() also forms a orthonormal coordinate system.
also forms a orthonormal coordinate system.
…It seems things are getting too mathematical and abstract (for me), thus for now I am going to wrap up what I have explained in this article .
We have seen
- Numerical matrices linearly transform vectors.
- Certain linear transformations do not change the direction of vectors in certain directions, which are called eigen vectors.
- Making use of eigen vectors, you can form new coordinate system which can describe the linear transformations in a more straightforward way.
- You can diagonalize a real symmetric matrix
 with an orthonormal matrix
with an orthonormal matrix 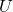 .
.
Of our current interest is what kind of linear transformation the real symmetric positive definite matrix enables. I am going to explain why the purple vectors in the figure above is swirling in the upcoming articles. Before that, however, we are going to see one application of what we have seen in this article, on dimension reduction. To be concrete the next article is going to be about principal component analysis (PCA), which is very important in many fields.
*In short, the orthonormal matrix ![]() , which I mentioned above enables rotation of matrix, and the diagonal matrix
, which I mentioned above enables rotation of matrix, and the diagonal matrix ![]() expands or contracts vectors along each axis. I am going to explain that more precisely in the upcoming articles.
expands or contracts vectors along each axis. I am going to explain that more precisely in the upcoming articles.
* I make study materials on machine learning, sponsored by DATANOMIQ. I do my best to make my content as straightforward but as precise as possible. I include all of my reference sources. If you notice any mistakes in my materials, including grammatical errors, please let me know (email: yasuto.tamura@datanomiq.de). And if you have any advice for making my materials more understandable to learners, I would appreciate hearing it.
*I attatched the codes I used to make the figures in this article. You can just copy, paste, and run, sometimes installing necessary libraries.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 |
import matplotlib.pyplot as plt import numpy as np import matplotlib.patches as mpatches T_A = np.array([[1, 1], [1, 0]]) total_step = 5 x = np.zeros((total_step, 2)) x[0] = np.array([1, 0]) for i in range(total_step - 1): x[i + 1] = np.dot(T_A, x[i]) eigen_values, eigen_vectors = np.linalg.eig(T_A) idx = eigen_values.argsort()[::-1] eigen_values = eigen_values[idx] eigen_vectors = eigen_vectors[:,idx] for i in range(len(eigen_vectors)): if(eigen_vectors.T[i][0] < 0): eigen_vectors.T[i] = - eigen_vectors.T[i] v_initial = x[0] v_coefficients = np.zeros((total_step , 2)) v_coefficients[0] = np.dot(v_initial , np.linalg.inv(eigen_vectors.T)) for i in range(total_step-1): v_coefficients[i + 1] = v_coefficients[i] * eigen_values v_1_list = np.zeros((total_step + 1, 2)) v_2_list = np.zeros((total_step + 1, 2)) for i in range(total_step): v_1_list[i+1] = v_coefficients.T[0][i]*eigen_vectors.T[0] v_2_list[i+1] = v_coefficients.T[1][i]*eigen_vectors.T[1] plt.figure(figsize=(20, 15)) fontsize = 20 small_shift = 0.2 plt.plot(x[:, 0], x[:, 1], marker='o', linestyle='none', markersize=10, color='black') plt.arrow(0, 0, eigen_vectors.T[0][0], eigen_vectors.T[0][1], width=0.05, head_width=0.2, color='orange') plt.arrow(0, 0, eigen_vectors.T[1][0], eigen_vectors.T[1][1], width=0.05, head_width=0.2, color='orange') plt.text(eigen_vectors.T[0][0], eigen_vectors.T[0][1]+small_shift, r'$v_{1}$', va='center',ha='right', fontsize=fontsize + 10) plt.text(eigen_vectors.T[1][0] - small_shift, eigen_vectors.T[1][1],r'$v_{2}$', va='center',ha='right', fontsize=fontsize + 10) for i in range(total_step): plt.arrow(0, 0, v_1_list[i+1][0], v_1_list[i+1][1], head_width=0.05, color='darkviolet', length_includes_head=True) plt.arrow(0, 0, v_2_list[i+1][0], v_2_list[i+1][1], head_width=0.05, color='darkviolet', length_includes_head=True) plt.text(v_1_list[i+1][0] + 2*small_shift , v_1_list[i+1][1]-2*small_shift,r'$\alpha \cdot \lambda_{0} ^{1} \cdot v_{2} $'.format(1,i+1, 1),va='center',ha='right', fontsize=fontsize) plt.text(v_2_list[i+1][0]-0.1, v_2_list[i+1][1],r'$\beta \cdot \lambda_{0} ^{1} \cdot v_{2} $'.format(2, i+1, 2),va='center',ha='right', fontsize=fontsize) plt.arrow(v_1_list[i+1][0], v_1_list[i+1][1], v_2_list[i+1][0], v_2_list[i+1][1], head_width=0, color='black', linestyle='--', length_includes_head=True) plt.arrow(v_2_list[i+1][0], v_2_list[i+1][1], v_1_list[i+1][0], v_1_list[i+1][1], head_width=0, color='black', linestyle='--', length_includes_head=True) orange_patch = mpatches.Patch(color='orange', label='Eigen vectors') purple_patch = mpatches.Patch(color='darkviolet', label='Scalar multiples of the eigen vectors') plt.legend(handles=[orange_patch, purple_patch], fontsize=25, loc='lower right') for i in range(total_step): plt.text(x[i][0]+0.1, x[i][1]-0.05, r'n={0}'.format(i), fontsize=20) plt.grid(True) plt.ylabel("$a_{n}: n^{th} generation$", fontsize=20) plt.xlabel("$a_{n+1}: n+1 ^{th} geneartion$", fontsize=20) plt.title("Fibonacci sequence and its eigen space", fontsize=30) #plt.savefig("Fibonacci_eigen_space.png") plt.show() |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 |
import matplotlib.pyplot as plt import numpy as np import matplotlib.patches as mpatches const_range = 10 X = np.arange(-const_range, const_range + 1, 1) Y = np.arange(-const_range, const_range + 1, 1) U_x, U_y = np.meshgrid(X, Y) T_A_0 = np.array([[3, 1], [1, 2]]) T_A_1 = np.array([[3, 1], [-1, 1]]) T_A_2 = np.array([[1, -1], [1, 1]]) T_A_list = np.array((T_A_0, T_A_1, T_A_2)) const_range = 5 plt.figure(figsize=(30, 10)) plt.subplots_adjust(wspace=0.1) labels = ["Grids", "Displacement vectors made by A", "Real eigen vectors of A"] title_list = [r"$A_1$ has two different real eigen vectors.", r"$A_2$ has two identical real unit eigen vectors.", r"$A_3$ has only imaginary eigen vectors."] for idx in range(len(T_A_list)): eigen_values, eigen_vectors = np.linalg.eig(T_A_list[idx]) sorted_idx = eigen_values.argsort()[::-1] eigen_values = eigen_values[sorted_idx] eigen_vectors = eigen_vectors[:,sorted_idx] eigen_vectors = eigen_vectors.astype(float) for i in range(len(eigen_vectors)): if(eigen_vectors.T[i][0] < 0): eigen_vectors.T[i] = - eigen_vectors.T[i] X = np.arange(-const_range, const_range + 1, 1) Y = np.arange(-const_range, const_range + 1, 1) U_x, U_y = np.meshgrid(X, Y) V_x = np.zeros((len(U_x), len(U_y))) V_y = np.zeros((len(U_x), len(U_y))) temp_vec = np.zeros((1, 2)) W_x = np.zeros((len(U_x), len(U_y))) W_y = np.zeros((len(U_x), len(U_y))) plt.subplot(1, 3, idx + 1) for i in range(len(U_x)): for j in range(len(U_y)): temp_vec[0][0] = U_x[i][j] temp_vec[0][1] = U_y[i][j] temp_vec[0] = np.dot(T_A_list[idx], temp_vec[0]) V_x[i][j] = temp_vec[0][0] V_y[i][j] = temp_vec[0][1] W_x[i][j] = V_x[i][j] - U_x[i][j] W_y[i][j] = V_y[i][j] - U_y[i][j] #plt.arrow(0, 0, V_x[i][j], V_y[i][j], head_width=0.1, color='red') plt.arrow(0, 0, U_x[i][j], U_y[i][j], head_width=0.3, color='dimgrey', label=labels[0]) plt.arrow(U_x[i][j], U_y[i][j], W_x[i][j], W_y[i][j], head_width=0.3, color='darkviolet', label=labels[1]) range_const = 20 plt.xlim([-range_const, range_const]) plt.ylim([-range_const, range_const]) plt.title(title_list[idx], fontsize=25) if idx==2: continue plt.arrow(0, 0, eigen_vectors.T[0][0]*10, eigen_vectors.T[0][1]*10, head_width=1, color='orange', label=labels[2]) plt.arrow(0, 0, eigen_vectors.T[1][0]*10, eigen_vectors.T[1][1]*10, head_width=1, color='orange', label=labels[2]) grey_patch = mpatches.Patch(color='grey', label='Grids') purple_patch = mpatches.Patch(color='darkviolet', label='Displacement vectors made by A') yellow_patch = mpatches.Patch(color='gold', label='Real eigen vectors of A') plt.legend(handles=[grey_patch, purple_patch, yellow_patch], fontsize=25, loc='lower right', bbox_to_anchor=(-0.1, -.35)) #plt.savefig("linear_transformation.png") plt.show() |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 |
# I borrowed codes from https://gist.github.com/WetHat/1d6cd0f7309535311a539b42cccca89c to make 3D arrows with matlotlib import numpy as np import matplotlib.pyplot as plt from mpl_toolkits.mplot3d.proj3d import proj_transform from mpl_toolkits.mplot3d.axes3d import Axes3D from matplotlib.text import Annotation from matplotlib.patches import FancyArrowPatch import matplotlib.patches as mpatches class Annotation3D(Annotation): def __init__(self, text, xyz, *args, **kwargs): super().__init__(text, xy=(0,0), *args, **kwargs) self._xyz = xyz def draw(self, renderer): x2, y2, z2 = proj_transform(*self._xyz, renderer.M) self.xy=(x2,y2) super().draw(renderer) def _annotate3D(ax,text, xyz, *args, **kwargs): '''Add anotation `text` to an `Axes3d` instance.''' annotation= Annotation3D(text, xyz, *args, **kwargs) ax.add_artist(annotation) setattr(Axes3D,'annotate3D',_annotate3D) class Arrow3D(FancyArrowPatch): def __init__(self, x, y, z, dx, dy, dz, *args, **kwargs): super().__init__((0,0), (0,0), *args, **kwargs) self._xyz = (x,y,z) self._dxdydz = (dx,dy,dz) def draw(self, renderer): x1,y1,z1 = self._xyz dx,dy,dz = self._dxdydz x2,y2,z2 = (x1+dx,y1+dy,z1+dz) xs, ys, zs = proj_transform((x1,x2),(y1,y2),(z1,z2), renderer.M) self.set_positions((xs[0],ys[0]),(xs[1],ys[1])) super().draw(renderer) def _arrow3D(ax, x, y, z, dx, dy, dz, *args, **kwargs): '''Add an 3d arrow to an `Axes3D` instance.''' arrow = Arrow3D(x, y, z, dx, dy, dz, *args, **kwargs) ax.add_artist(arrow) setattr(Axes3D,'arrow3D',_arrow3D) T_A = np.array([[60.45, 33.63, 46.29], [33.63, 68.49, 50.93], [46.29, 50.93, 53.61]]) T_A = T_A/50 const_range = 2 X = np.arange(-const_range, const_range + 1, 1) Y = np.arange(-const_range, const_range + 1, 1) Z = np.arange(-const_range, const_range + 1, 1) U_x, U_y, U_z = np.meshgrid(X, Y, Z) V_x = np.zeros((len(U_x), len(U_y), len(U_z))) V_y = np.zeros((len(U_x), len(U_y), len(U_z))) V_z = np.zeros((len(U_x), len(U_y), len(U_z))) temp_vec = np.zeros((1, 3)) W_x = np.zeros((len(U_x), len(U_y), len(U_z))) W_y = np.zeros((len(U_x), len(U_y), len(U_z))) W_z = np.zeros((len(U_x), len(U_y), len(U_z))) eigen_values, eigen_vectors = np.linalg.eig(T_A) sorted_idx = eigen_values.argsort()[::-1] eigen_values = eigen_values[sorted_idx] eigen_vectors = eigen_vectors[:,sorted_idx] eigen_vectors = eigen_vectors.astype(float) fig = plt.figure(figsize=(15, 15)) ax = fig.add_subplot(111, projection='3d') grid_range = const_range + 5 ax.set_xlim(-grid_range, grid_range) ax.set_ylim(-grid_range, grid_range) ax.set_zlim(-grid_range, grid_range) eigen_values, eigen_vectors = np.linalg.eig(T_A) sorted_idx = eigen_values.argsort()[::-1] eigen_values = eigen_values[sorted_idx] eigen_vectors = eigen_vectors[:,sorted_idx] eigen_vectors = eigen_vectors.astype(float) for i in range(len(eigen_vectors)): if(eigen_vectors.T[i][0] < 0): eigen_vectors.T[i] = - eigen_vectors.T[i] for i in range(len(U_x)): for j in range(len(U_x)): for k in range(len(U_x)): temp_vec[0][0] = U_x[i][j][k] temp_vec[0][1] = U_y[i][j][k] temp_vec[0][2] = U_z[i][j][k] temp_vec[0] = np.dot(T_A, temp_vec[0]) V_x[i][j][k] = temp_vec[0][0] V_y[i][j][k] = temp_vec[0][1] V_z[i][j][k] = temp_vec[0][2] W_x[i][j][k] = V_x[i][j][k] - U_x[i][j][k] W_y[i][j][k] = V_y[i][j][k] - U_y[i][j][k] W_z[i][j][k] = V_z[i][j][k] - U_z[i][j][k] ax.arrow3D(0, 0, 0, U_x[i][j][k], U_y[i][j][k], U_z[i][j][k], mutation_scale=10, arrowstyle="-|>", fc='dimgrey', ec='dimgrey') #ax.arrow3D(0, 0, 0, # V_x[i][j][k], V_y[i][j][k], V_z[i][j][k], # mutation_scale=10, arrowstyle="-|>", fc='red', ec='red') ax.arrow3D(U_x[i][j][k], U_y[i][j][k], U_z[i][j][k], W_x[i][j][k], W_y[i][j][k], W_z[i][j][k], mutation_scale=10, arrowstyle="-|>", fc='darkviolet', ec='darkviolet') ax.arrow3D(0, 0, 0, eigen_vectors.T[0][0]*10, eigen_vectors.T[0][1]*10, eigen_vectors.T[0][2]*10, mutation_scale=10, arrowstyle="-|>", fc='orange', ec='orange') ax.arrow3D(0, 0, 0, eigen_vectors.T[1][0]*10, eigen_vectors.T[1][1]*10, eigen_vectors.T[1][2]*10, mutation_scale=10, arrowstyle="-|>", fc='orange', ec='orange') ax.arrow3D(0, 0, 0, eigen_vectors.T[2][0]*10, eigen_vectors.T[2][1]*10, eigen_vectors.T[2][2]*10, mutation_scale=10, arrowstyle="-|>", fc='orange', ec='orange') ax.text(eigen_vectors.T[0][0]*8 , eigen_vectors.T[0][1]*8, eigen_vectors.T[0][2]*8+1, r'$v_1$', fontsize=20) ax.text(eigen_vectors.T[1][0]*8 , eigen_vectors.T[1][1]*8, eigen_vectors.T[1][2]*8, r'$v_2$', fontsize=20) ax.text(eigen_vectors.T[2][0]*8 , eigen_vectors.T[2][1]*8, eigen_vectors.T[2][2]*8, r'$v_3$', fontsize=20) grey_patch = mpatches.Patch(color='grey', label='Grids') orange_patch = mpatches.Patch(color='orange', label='Orthogonal eigen vectors of A') purple_patch = mpatches.Patch(color='darkviolet', label='Displacement vectors made by A') plt.legend(handles=[grey_patch, orange_patch, purple_patch], fontsize=20, loc='lower right') ax.set_xlabel(r'$x_1$', fontsize=25) ax.set_ylabel(r'$x_2$', fontsize=25) ax.set_zlabel(r'$x_3$', fontsize=25) #plt.savefig("symmetric_positive_definite_visualizaiton.png") plt.show() |

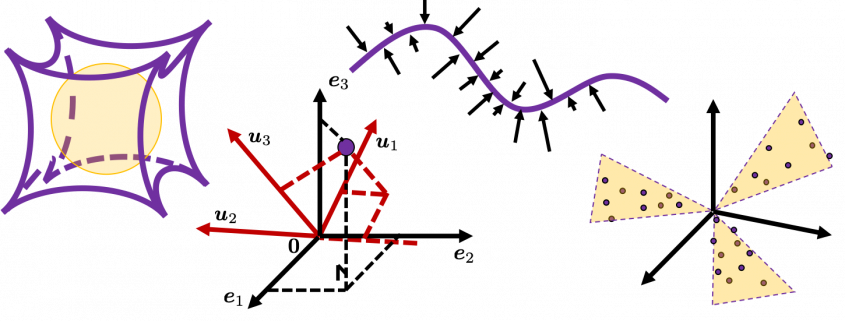








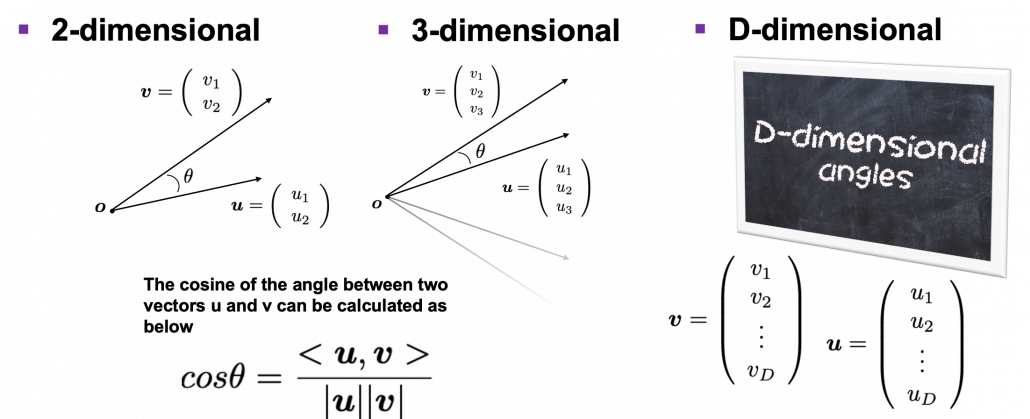
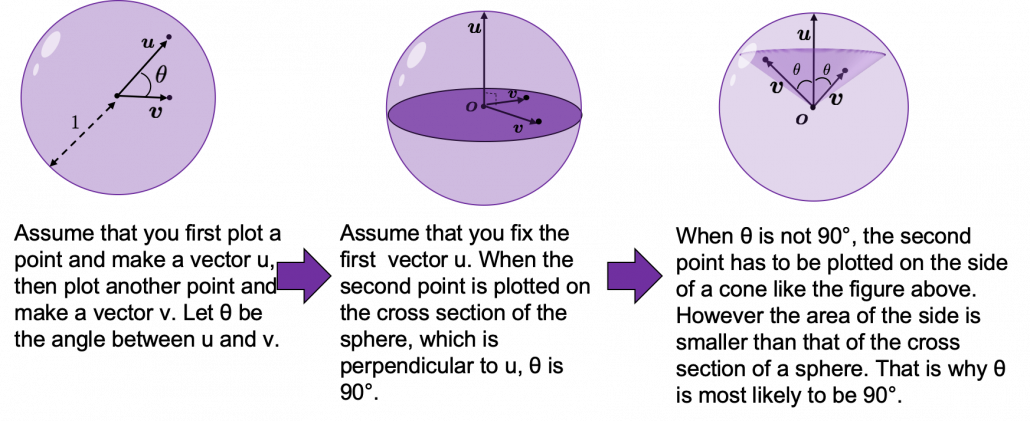
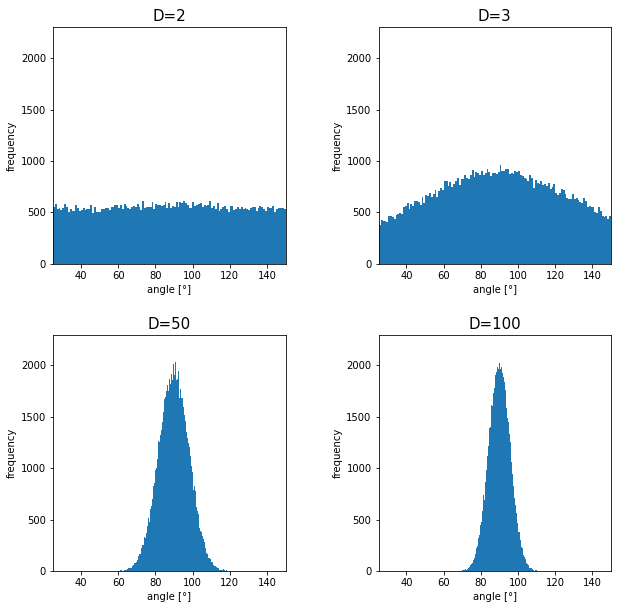
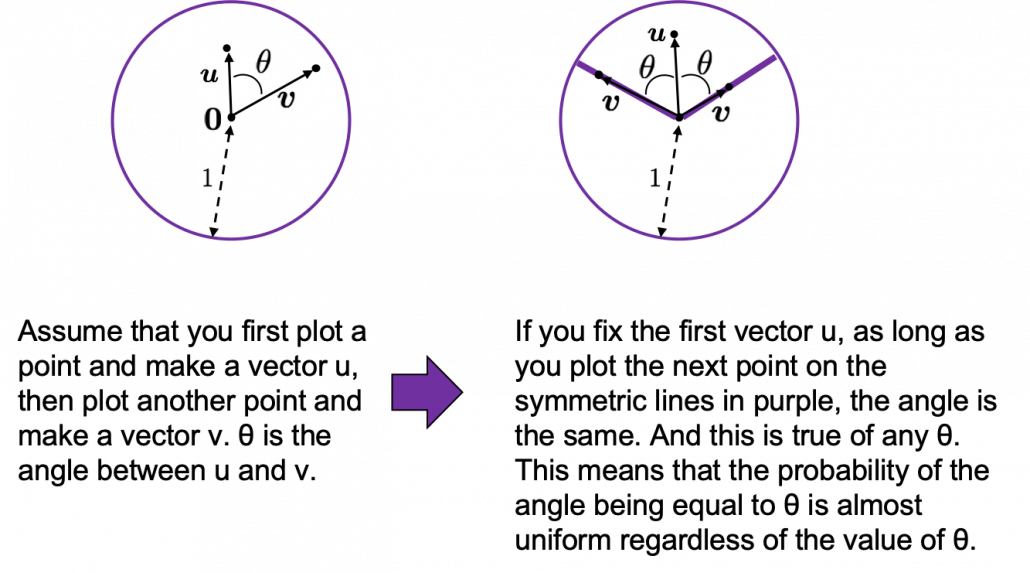 How about in 3-dimensional space? In fact the distribution of
How about in 3-dimensional space? In fact the distribution of