Tag Archive for: Data Science

Attribution Modelling using Data Science and Deep LearningDATANOMIQ
Alexander Lammers

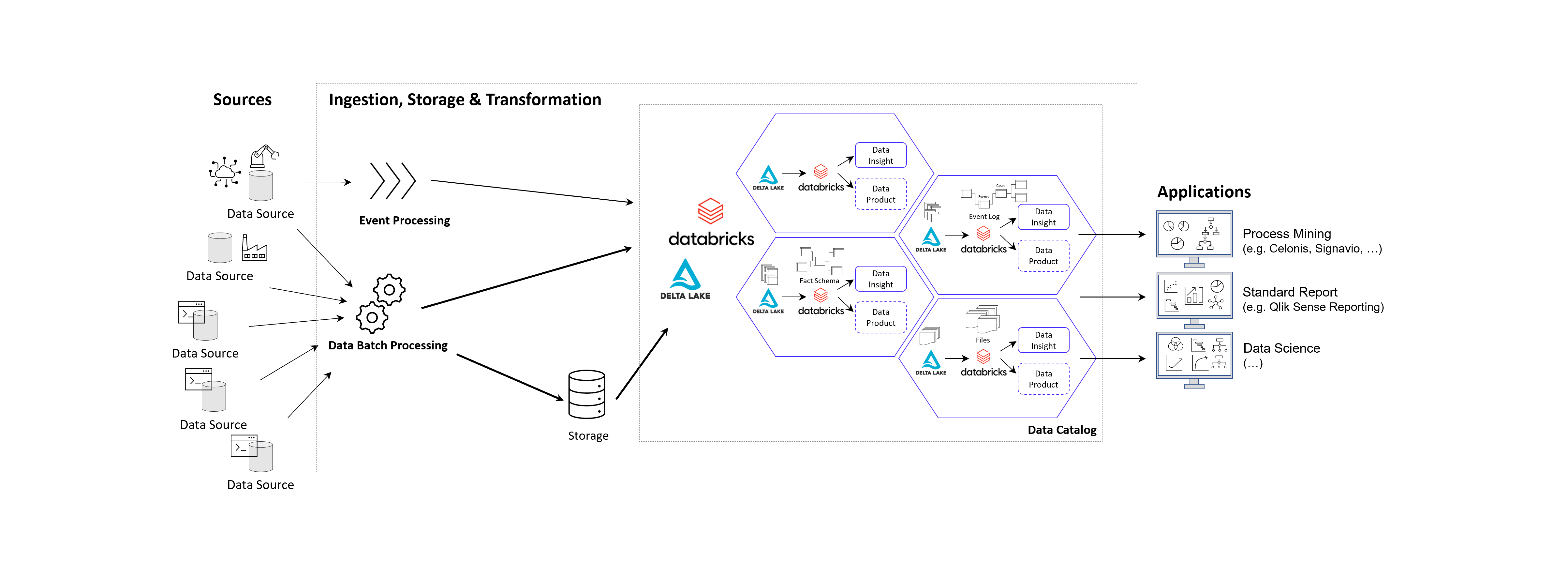
Data-driven Attribution Modeling

/in , , , , , , , /by

In the world of commerce, companies often face the temptation to reduce their marketing spending, especially during times of economic uncertainty or when planning to cut costs. However, this short-term strategy can lead to long-term consequences that may hinder a company’s growth and competitiveness in the market.

Maintaining a consistent marketing presence is crucial for businesses, as it helps to keep the company at the forefront of their target audience’s minds. By reducing marketing efforts, companies risk losing visibility and brand awareness among potential clients, which can be difficult and expensive to regain later. Moreover, a strong marketing strategy is essential for building trust and credibility with prospective customers, as it demonstrates the company’s expertise, values, and commitment to their industry.

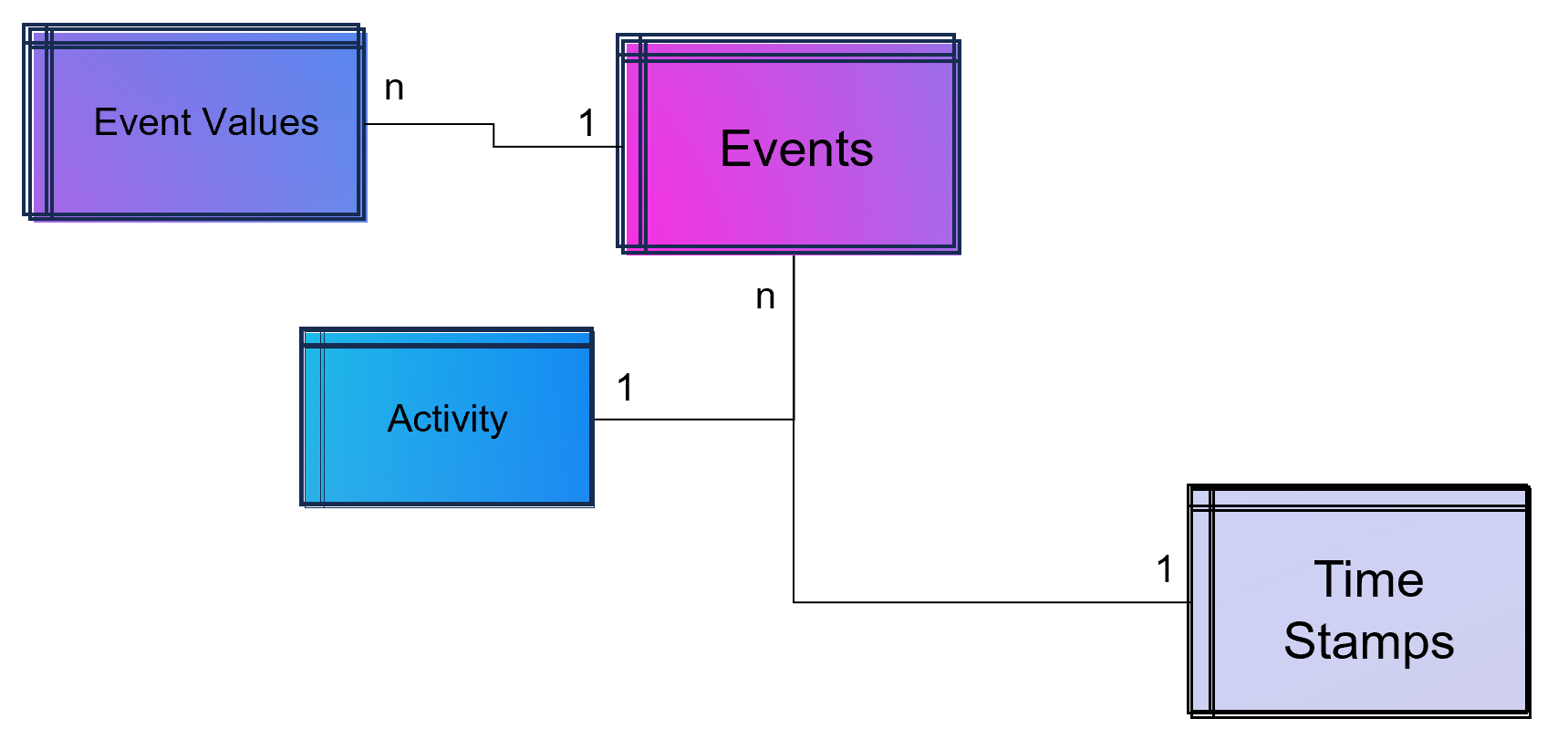
Given a fixed budget, companies apply economic principles for marketing efforts and need to spend a given marketing budget as efficient as possible. In this view, attribution models are an essential tool for companies to understand the effectiveness of their marketing efforts and optimize their strategies for maximum return on investments (ROI). By assigning optimal credit to various touchpoints in the customer journey, these models provide valuable insights into which channels, campaigns, and interactions have the greatest impact on driving conversions and therefore revenue. Identifying the most important channels enables companies to distribute the given budget accordingly in an optimal way.

1. Combining business value with attribution modeling

The true value of attribution modeling lies not solely in applying the optimal theoretical concept – that are discussed below – but in the practical application in coherence with the business logic of the firm. Therefore, the correct modeling ensures that companies are not only distributing their budget in an optimal way but also that they incorporate the business logic to focus on an optimal long-term growth strategy.

Understanding and incorporating business logic into attribution models is the critical step that is often overlooked or poorly understood. However, it is the key to unlocking the full potential of attribution modeling and making data-driven decisions that align with business goals. Without properly integrating the business logic, even the most sophisticated attribution models will fail to provide actionable insights and may lead to misguided marketing strategies.

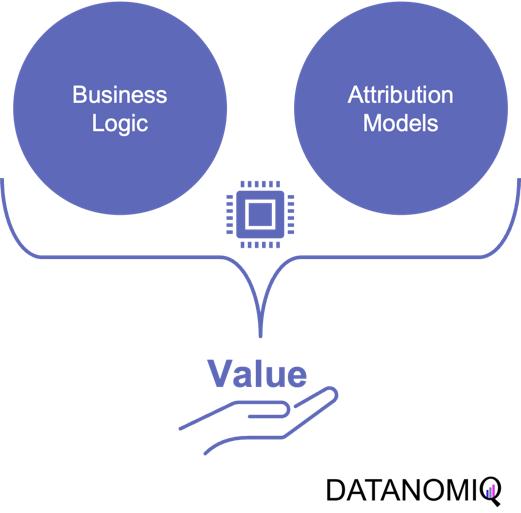
Figure 1 – Combining the business logic with attribution modeling to generate value for firms

Figure 1 – Combining the business logic with attribution modeling to generate value for firms

For example, determining the end of a customer journey is a critical step in attribution modeling. When there are long gaps between customer interactions and touchpoints, analysts must carefully examine the data to decide if the current journey has concluded or is still ongoing. To make this determination, they need to consider the length of the gap in relation to typical journey durations and assess whether the gap follows a common sequence of touchpoints. By analyzing this data in an appropriate way, businesses can more accurately assess the impact of their marketing efforts and avoid attributing credit to touchpoints that are no longer relevant.

Another important consideration is accounting for conversions that ultimately lead to returns or cancellations. While it’s easy to get excited about the number of conversions generated by marketing campaigns, it’s essential to recognize that not all conversions should be valued equal. If a significant portion of conversions result in returns or cancellations, the true value of those campaigns may be much lower than initially believed.

To effectively incorporate these factors into attribution models, businesses need to important things. First, a robust data platform (such as a customer data platform; CDP) that can integrate data from various sources, such as tracking systems, ERP systems, e-commerce platforms to effectively perform data analytics. This allows for a holistic view of the customer journey, including post-conversion events like returns and cancellations, which are crucial for accurate attribution modeling. Second, as outlined above, businesses need a profound understanding of the business model and logic.

2. On the Relevance of Attribution Models in Online Marketing

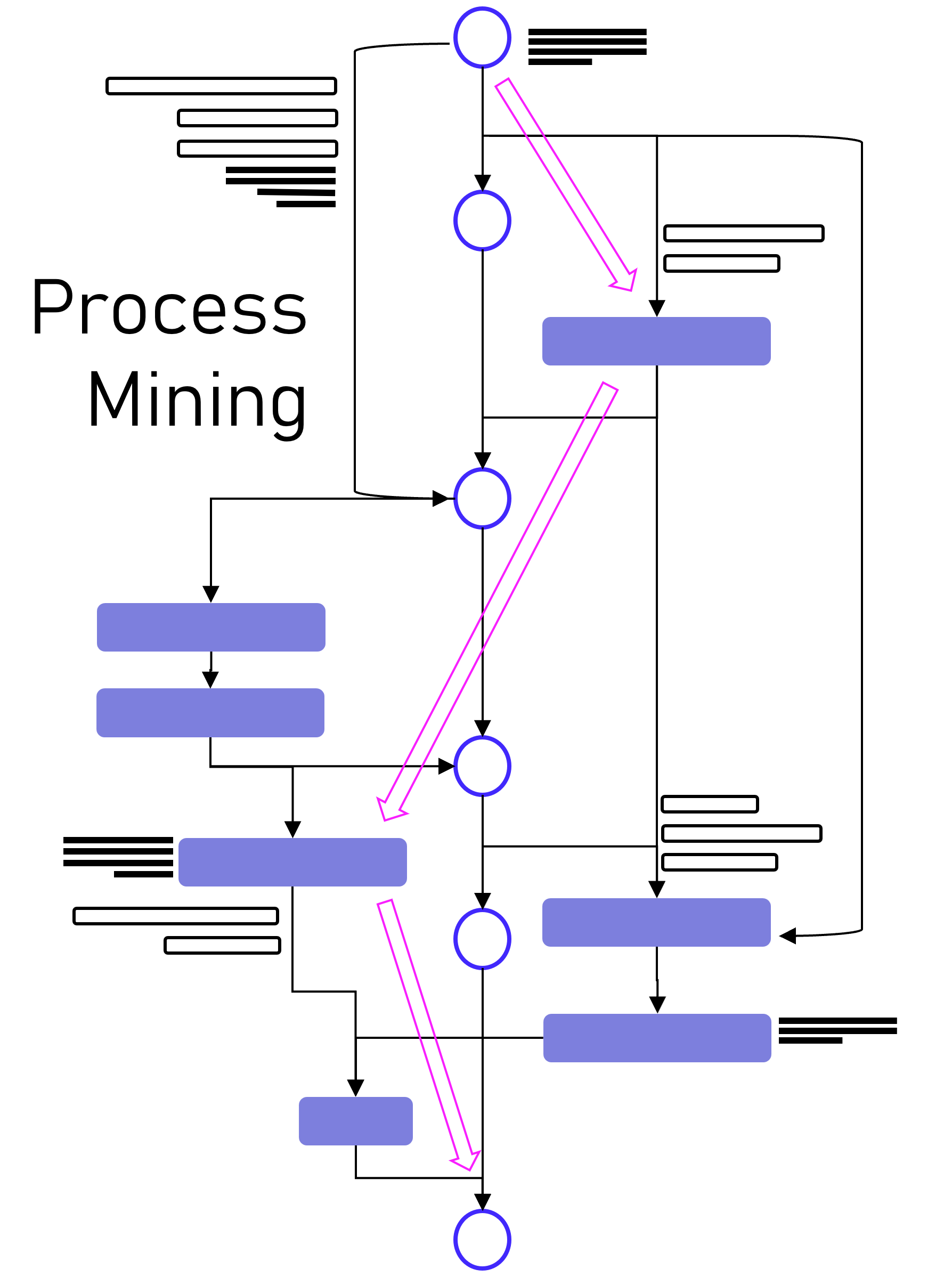
A conversion is a point in the customer journey where a recipient of a marketing message performs a somewhat desired action. For example, open an email, click on a call-to-action link or go to a landing page and fill out a registration. Finally, the ultimate conversion would be of course buying the product. Attribution models serve as frameworks that help marketers assess the business impact of different channels on a customer’s decision to convert along a customer´s journey. By providing insights into which interactions most effectively drive sales, these models enable more efficient resource allocation given a fixed budget.

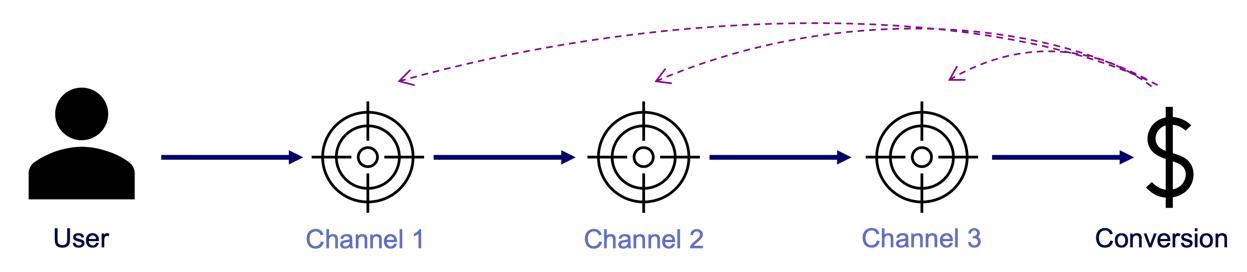
Figure 2 - A simple illustration of one single customer journey. Consider that from the company’s perspective all journeys together result into a complex network of possible journey steps.

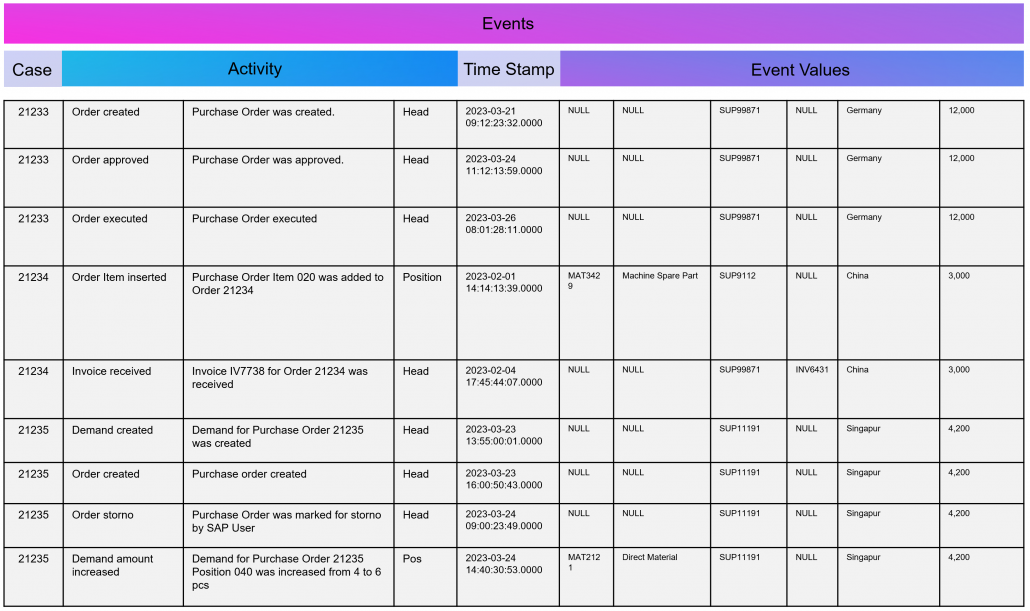
Figure 2 – A simple illustration of one single customer journey. Consider that from the company’s perspective all journeys together result into a complex network of possible journey steps.

Companies typically utilize a diverse marketing mix, including email marketing, search engine advertising (SEA), search engine optimization (SEO), affiliate marketing, and social media. Attribution models facilitate the analysis of customer interactions across these touchpoints, offering a comprehensive view of the customer journey.

  • Comprehensive Customer Insights: By identifying the most effective channels for driving conversions, attribution models allow marketers to tailor strategies that enhance customer engagement and improve conversion rates.

  • Optimized Budget Allocation: These models reveal the performance of various marketing channels, helping marketers allocate budgets more efficiently. This ensures that resources are directed towards channels that offer the highest return on investment (ROI), maximizing marketing impact.

  • Data-Driven Decision Making: Attribution models empower marketers to make informed, data-driven decisions, leading to more effective campaign strategies and better alignment between marketing and sales efforts.

In the realm of online advertising, evaluating media effectiveness is a critical component of the decision-making process. Since advertisement costs often depend on clicks or impressions, understanding each channel’s effectiveness is vital. A multi-channel attribution model is necessary to grasp the marketing impact of each channel and the overall effectiveness of online marketing activities. This approach ensures optimal budget allocation, enhances ROI, and drives successful marketing outcomes.

What types of attribution models are there? Depending on the attribution model, different values are assigned to various touchpoints. These models help determine which channels are the most important and should be prioritized. Each channel is assigned a monetary value based on its contribution to success. This weighting then determines the allocation of the marketing budget. Below are some attribution models commonly used in marketing practice.

2.1. Single-Touch Attribution Models

As it follows from the name of the group of these approaches, they consider only one touchpoint.

2.1.1 First Touch Attribution

First touch attribution is the standard and simplest method for attributing conversions, as it assigns full credit to the first interaction. One of its main advantages is its simplicity; it is a straightforward and easy-to-understand approach. Additionally, it allows for quick implementation without the need for complex calculations or data analysis, making it a convenient choice for organizations looking for a simple attribution method. This model can be particularly beneficial when the focus is solely on demand generation. However, there are notable drawbacks to first touch attribution. It tends to oversimplify the customer journey by ignoring the influence of subsequent touchpoints. This can lead to a limited view of channel performance, as it may disproportionately credit channels that are more likely to be the first point of contact, potentially overlooking the contributions of other channels that assist in conversions.

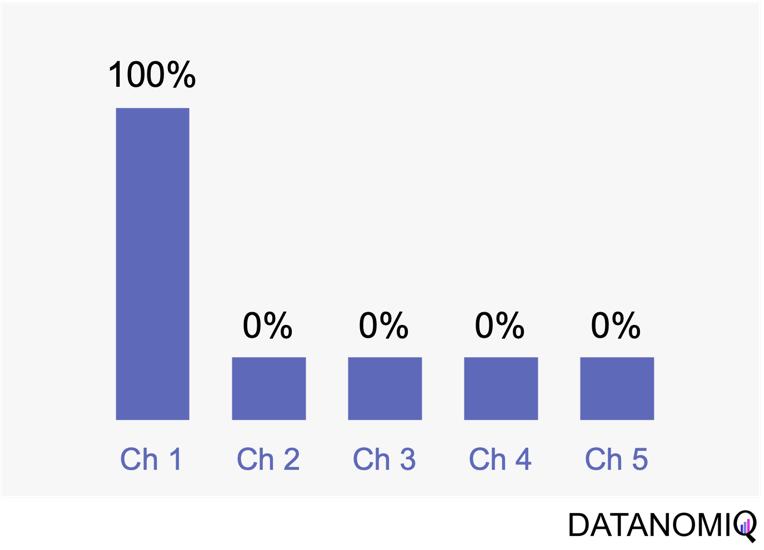
Figure 3 - The first touch is a simple non-intelligent way of attribution.

Figure 3 – The first touch is a simple non-intelligent way of attribution.

2.1.2 Last Touch Attribution

Last touch attribution is another straightforward method for attributing conversions, serving as the opposite of first touch attribution by assigning full credit to the last interaction. Its simplicity is one of its main advantages, as it is easy to understand and implement without the need for complex calculations or data analysis. This makes it a convenient choice for organizations seeking a simple attribution approach, especially when the focus is solely on driving conversions. However, last touch attribution also has its drawbacks. It tends to oversimplify the customer journey by neglecting the influence of earlier touchpoints. This approach provides limited insights into the full customer journey, as it focuses solely on the last touchpoint and overlooks the cumulative impact of multiple touchpoints, missing out on valuable insights.

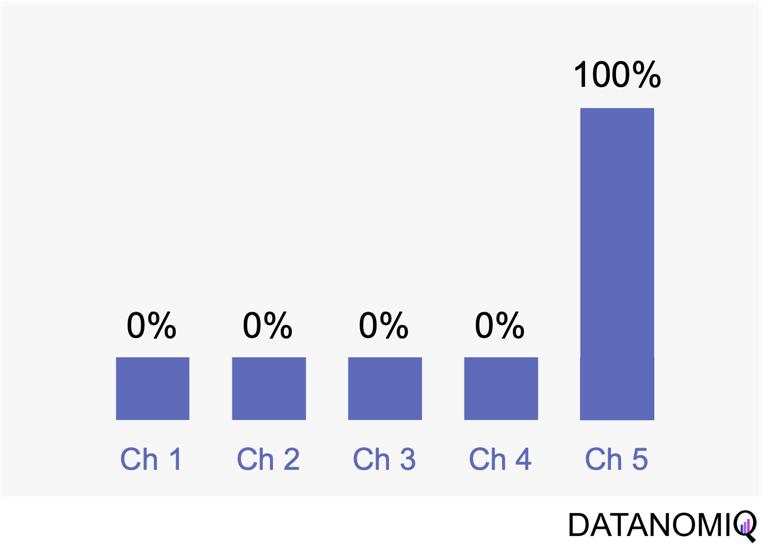
Figure 4 - Last touch attribution is the counterpart to the first touch approach.

Figure 4 – Last touch attribution is the counterpart to the first touch approach.

2.2 Multi-Touch Attribution Models

We noted that single-touch attribution models are easy to interpret and implement. However, these methods often fall short in assigning credit, as they apply rules arbitrarily and fail to accurately gauge the contribution of each touchpoint in the consumer journey. As a result, marketers may make decisions based on skewed data. In contrast, multi-touch attribution leverages individual user-level data from various channels. It calculates and assigns credit to the marketing touchpoints that have influenced a desired business outcome for a specific key performance indicator (KPI) event.

2.2.1 Linear Attribution

Linear attribution is a standard approach that improves upon single-touch models by considering all interactions and assigning them equal weight. For instance, if there are five touchpoints in a customer’s journey, each would receive 20% of the credit for the conversion. This method offers several advantages. Firstly, it ensures equal distribution of credit across all touchpoints, providing a balanced representation of each touchpoint’s contribution to conversions. This approach promotes fairness by avoiding the overemphasis or neglect of specific touchpoints, ensuring that credit is distributed evenly among channels. Additionally, linear attribution is easy to implement, requiring no complex calculations or data analysis, which makes it a convenient choice for organizations seeking a straightforward attribution method. However, linear attribution also has its drawbacks. One significant limitation is its lack of differentiation, as it assigns equal credit to each touchpoint regardless of their actual impact on driving conversions. This can lead to an inaccurate representation of the effectiveness of individual touchpoints. Furthermore, linear attribution ignores the concept of time decay, meaning it does not account for the diminishing influence of earlier touchpoints over time. It treats all touchpoints equally, regardless of their temporal proximity to the conversion event, potentially overlooking the greater impact of more recent interactions.

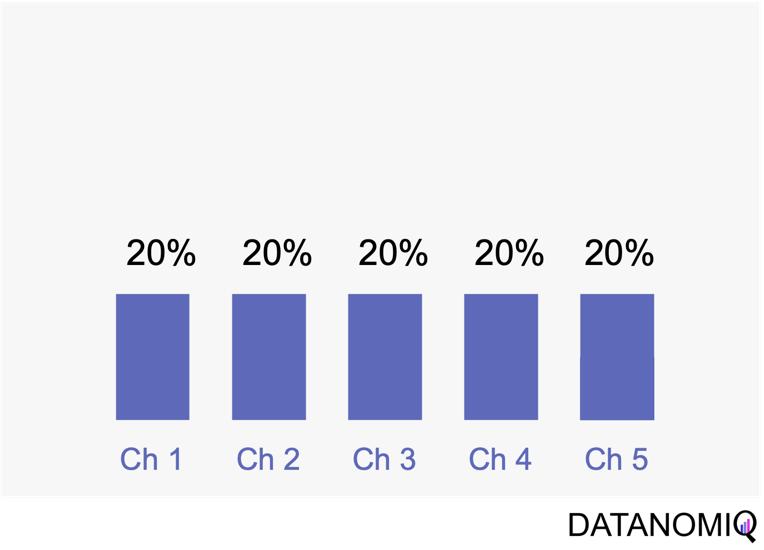
Figure 5 - Linear uniform attribution.

Figure 5 – Linear uniform attribution.

2.2.2 Position-based Attribution (U-Shaped Attribution & W-Shaped Attribution)

Position-based attribution, encompassing both U-shaped and W-shaped models, focuses on assigning the most significant weight to the first and last touchpoints in a customer’s journey. In the W-shaped attribution model, the middle touchpoint also receives a substantial amount of credit. This approach offers several advantages. One of the primary benefits is the weighted credit system, which assigns more credit to key touchpoints such as the first and last interactions, and sometimes additional key touchpoints in between. This allows marketers to highlight the importance of these critical interactions in driving conversions. Additionally, position-based attribution provides flexibility, enabling businesses to customize and adjust the distribution of credit according to their specific objectives and customer behavior patterns. However, there are some drawbacks to consider. Position-based attribution involves a degree of subjectivity, as determining the specific weights for different touchpoints requires subjective decision-making. The choice of weights can vary across organizations and may affect the accuracy of the attribution results. Furthermore, this model has limited adaptability, as it may not fully capture the nuances of every customer journey, given its focus on specific positions or touchpoints.

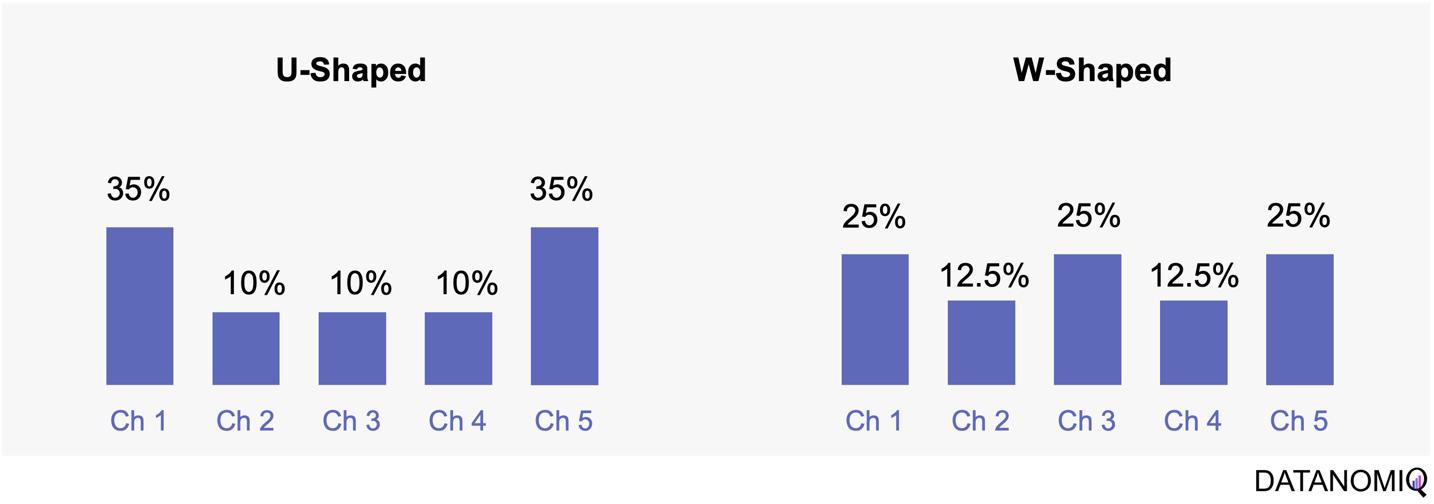
Figure 6 - The U-shaped attribution (sometimes known as "bathtube model" and the W-shaped one are first attempts of weighted models.

Figure 6 – The U-shaped attribution (sometimes known as “bathtube model” and the W-shaped one are first attempts of weighted models.

2.2.3 Time Decay Attribution

Time decay attribution is a model that primarily assigns most of the credit to interactions that occur closest to the point of conversion. This approach has several advantages. One of its key benefits is temporal sensitivity, as it recognizes the diminishing impact of earlier touchpoints over time. By assigning more credit to touchpoints closer to the conversion event, it reflects the higher influence of recent interactions. Additionally, time decay attribution offers flexibility, allowing organizations to customize the decay rate or function. This enables businesses to fine-tune the model according to their specific needs and customer behavior patterns, which can be particularly useful for fast-moving consumer goods (FMCG) companies. However, time decay attribution also has its drawbacks. One challenge is the arbitrary nature of the decay function, as determining the appropriate decay rate is both challenging and subjective. There is no universally optimal decay function, and choosing an inappropriate model can lead to inaccurate credit distribution. Moreover, this approach may oversimplify time dynamics by assuming a linear or exponential decay pattern, which might not fully capture the complex temporal dynamics of customer behavior. Additionally, time decay attribution primarily focuses on the temporal aspect and may overlook other contextual factors that influence touchpoint effectiveness, such as channel interactions, customer segments, or campaign-specific dynamics.

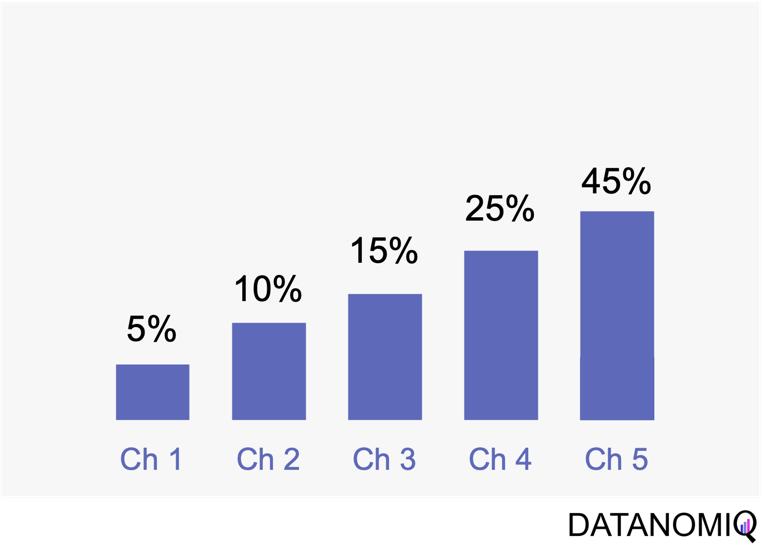
Figure 7 - Time-based models can be configurated by according to the first or last touch and weighted by the timespan in between of each touchpoint.

Figure 7 – Time-based models can be configurated by according to the first or last touch and weighted by the timespan in between of each touchpoint.

2.3 Data-Driven Attribution Models

2.3.1 Markov Chain Attribution

Markov chain attribution is a data-driven method that analyzes marketing effectiveness using the principles of Markov Chains. Those chains are mathematical models used to describe systems that transition from one state to another in a chain-like process. The principles focus on the transition matrix, derived from analyzing customer journeys from initial touchpoints to conversion or no conversion, to capture the sequential nature of interactions and understand how each touchpoint influences the final decision. Let’s have a look at the following simple example with three channels that are chained together and leading to either a conversion or no conversion.

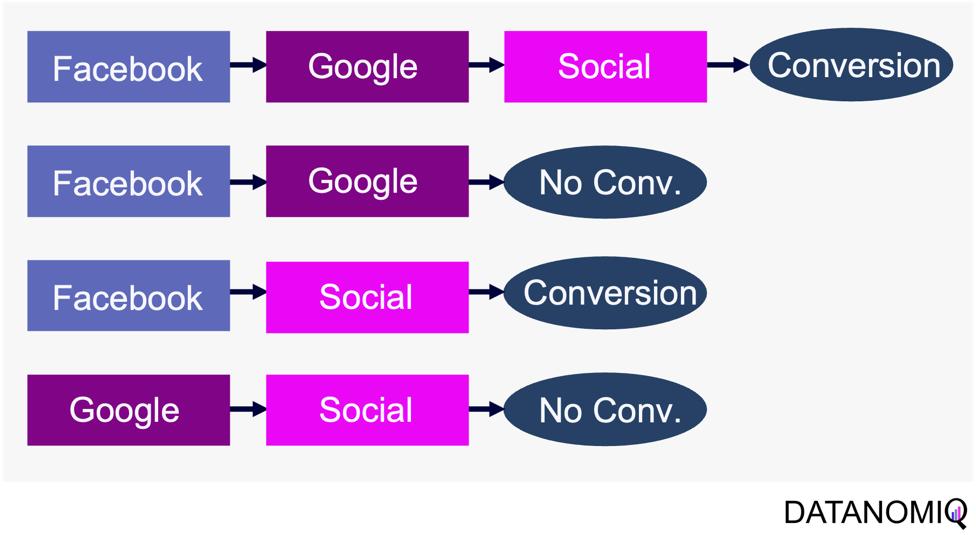
Figure 8 - Example of four customer journeys

Figure 8 – Example of four customer journeys

The model calculates the conversion likelihood by examining transitions between touchpoints. Those transitions are depicted in the following probability tree.

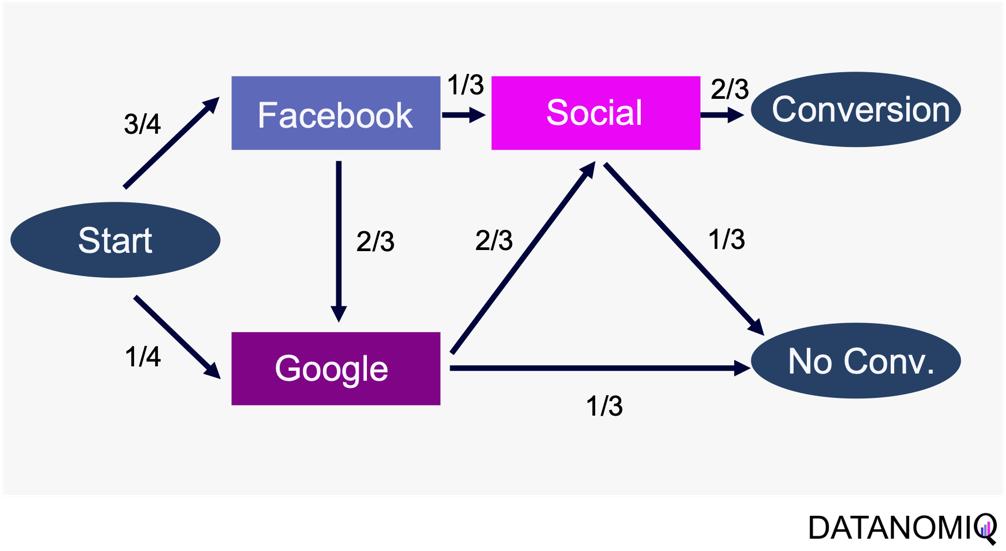
Figure 9 - Example of a touchpoint network based on customer journeys

Figure 9 – Example of a touchpoint network based on customer journeys

Based on this tree, the transition matrix can be constructed that reveals the influence of each touchpoint and thus the significance of each channel.

This method considers the sequential nature of customer journeys and relies on historical data to estimate transition probabilities, capturing the empirical behavior of customers. It offers flexibility by allowing customization to incorporate factors like time decay, channel interactions, and different attribution rules.

Markov chain attribution can be extended to higher-order chains, where the probability of transition depends on multiple previous states, providing a more nuanced analysis of customer behavior. To do so, the Markov process introduces a memory parameter 0 that is assumed to be zero here. Overall, it offers a robust framework for understanding the influence of different marketing touchpoints.

2.3.2 Shapley Value Attribution (Game Theoretical Approach)

The Shapley value is a concept from game theory that provides a fair method for distributing rewards among participants in a coalition. It ensures that both gains and costs are allocated equitably among actors, making it particularly useful when individual contributions vary but collective efforts lead to a shared outcome. In advertising, the Shapley method treats the advertising channels as players in a cooperative game. Now, consider a channel coalition consisting of different advertising channels . The utility function describes the contribution of a coalition of channels .

In this formula, is the cardinality of a specific coalition and the sum extends over all subsets of that do not contain the marginal contribution of channel to the coalition . For more information on how to calculate the marginal distribution, see Zhao et al. (2018).

The Shapley value approach ensures a fair allocation of credit to each touchpoint based on its contribution to the conversion process. This method encourages cooperation among channels, fostering a collaborative approach to achieving marketing goals. By accurately assessing the contribution of each channel, marketers can gain valuable insights into the performance of their marketing efforts, leading to more informed decision-making. Despite its advantages, the Shapley value method has some limitations. The method can be sensitive to the order in which touchpoints are considered, potentially leading to variations in results depending on the sequence of attribution. This sensitivity can impact the consistency of the outcomes. Finally, Shapley value and Markov chain attribution can also be combined using an ensemble attribution model to further reduce the generalization error (Gaur & Bharti 2020).

2.33. Algorithmic Attribution using binary Classifier and (causal) Machine Learning

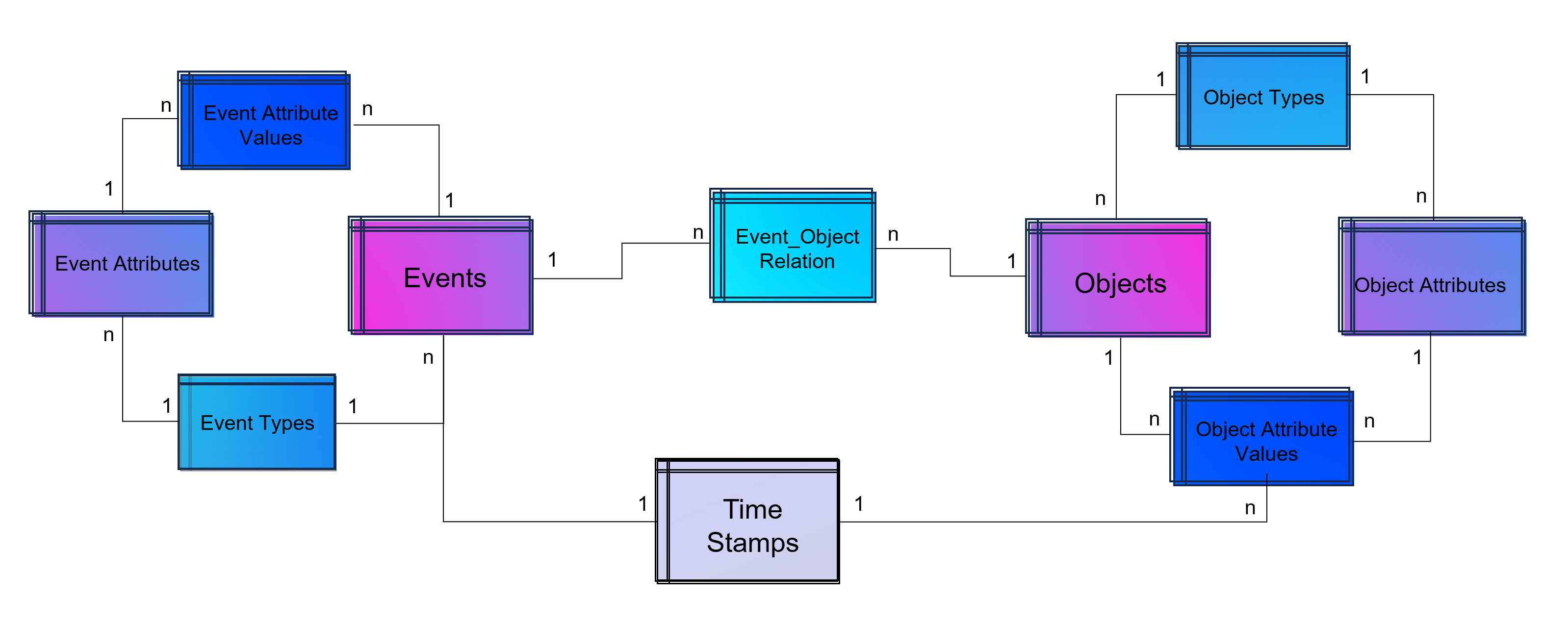
While customer journey data often suffices for evaluating channel contributions and strategy formulation, it may not always be comprehensive enough. Fortunately, companies frequently possess a wealth of additional data that can be leveraged to enhance attribution accuracy by using a variety of analytics data from various vendors. For examples, companies might collect extensive data, including customer website activity such as clicks, page views, and conversions. This data includes features like for example the Urchin Tracking Module (UTM) information such as source, medium, campaign, content and term as well as campaign, device type, geographical information, number of user engagements, and scroll frequency, among others.

Utilizing this information, a binary classification model can be trained to predict the probability of conversion at each step of the multi touch attribution (MTA) model. This approach not only identifies the most effective channels for conversions but also highlights overvalued channels. Common algorithms include logistic regressions to easily predict the probability of conversion based on various features. Gradient boosting also provides a popular ensemble technique that is often used for unbalanced data, which is quite common in attribution data. Moreover, random forest models as well as support vector machines (SVMs) are also frequently applied. When it comes to deep learning models, that are often used for more complex problems and sequential data, Long Short-Term Memory (LSTM) networks or Transformers are applied. Those models can capture the long-range dependencies among multiple touchpoints.

Figure 10 - Attribution Model based on Deep Learning / AI

Figure 10 – Attribution Model based on Deep Learning / AI

The approach is scalable, capable of handling large volumes of data, making it ideal for organizations with extensive marketing campaigns and complex customer journeys. By leveraging advanced algorithms, it offers more accurate attribution of credit to different touchpoints, enabling marketers to make informed, data-driven decisions.

All those models are part of the Machine Learning & AI Toolkit for assessing MTA. And since the business world is evolving quickly, newer methods such as double Machine Learning or causal forest models that are discussed in the marketing literature (e.g. Langen & Huber 2023) in combination with eXplainable Artificial Intelligence (XAI) can also be applied as well in the DATANOMIQ Machine Learning and AI framework.

3. Conclusion

As digital marketing continues to evolve in the age of AI, attribution models remain crucial for understanding the complex customer journey and optimizing marketing strategies. These models not only aid in effective budget allocation but also provide a comprehensive view of how different channels contribute to conversions. With advancements in technology, particularly the shift towards data-driven and multi-touch attribution models, marketers are better equipped to make informed decisions that enhance quick return on investment (ROI) and maintain competitiveness in the digital landscape.

Several trends are shaping the evolution of attribution models. The increasing use of machine learning in marketing attribution allows for more precise and predictive analytics, which can anticipate customer behavior and optimize marketing efforts accordingly. Additionally, as privacy regulations become more stringent, there is a growing focus on data quality and ethical data usage (Ethical AI), ensuring that attribution models are both effective and compliant. Furthermore, the integration of view-through attribution, which considers the impact of ad impressions that do not result in immediate clicks, provides a more holistic understanding of customer interactions across channels. As these models become more sophisticated, they will likely incorporate a wider array of data points, offering deeper insights into the customer journey.

Unlock your marketing potential with a strategy session with our DATANOMIQ experts. Discover how our solutions can elevate your media-mix models and boost your organization by making smarter, data-driven decisions.

References

  • Zhao, K., Mahboobi, S. H., & Bagheri, S. R. (2018). Shapley value methods for attribution modeling in online advertising. arXiv preprint arXiv:1804.05327.
  • Gaur, J., & Bharti, K. (2020). Attribution modelling in marketing: Literature review and research agenda. Academy of Marketing Studies Journal, 24(4), 1-21.
  • Langen H, Huber M (2023) How causal machine learning can leverage marketing strategies: Assessing and improving the performance of a coupon campaign. PLoS ONE 18(1): e0278937. https://doi.org/10.1371/journal. pone.0278937

Process Mining / Process Analytics
Benjamin Aunkofer

Process Mining – Ist Celonis wirklich so gut? Ein Praxisbericht.

/in , , , , , , /by

Diese Artikel wird viel gelesen werden. Von Process Mining Kunden, von Process Mining Beratern und von Process Mining Software-Anbietern. Und ganz besonders von Celonis.

Der Gartner´s Magic Quadrant zu Process Mining Tools für 2024 zeigt einige Movements im Vergleich zu 2023. Jeder kennt den Gartner Magic Quadrant, nicht nur für Process Mining Tools sondern für viele andere Software-Kategorien und auch für Dienstleistungen/Beratungen. Gartner gilt längst als der relevanteste und internationale Benchmark.

Process Mining – Wo stehen wir heute?

Eine Einschränkung dazu vorweg: Ich kann nur für den deutschen Markt sprechen. Zwar verfolge ich mit Spannung die ersten Erfolge von Celonis in den USA und in Japan, aber ich bin dort ja nicht selbst tätig. Ich kann lediglich für den Raum D/A/CH sprechen, in dem ich für Unternehmen in nahezu allen Branchen zu Process Mining Beratung und gemeinsam mit meinem Team Implementierung anbiete. Dabei arbeiten wir technologie-offen und mit nahezu allen Tools – Und oft in enger Verbindung mit Initiativen der Business Intelligence und Data Science. Wir sind neutral und haben keine “Aktien” in irgendeinem Process Mining Tool!

Process Mining wird heute in allen DAX-Konzernen und auch in allen MDAX-Unternehmen eingesetzt. Teilweise noch als Nischenanalytik, teilweise recht großspurig wie es z. B. die Deutsche Telekom oder die Lufthansa tun.

Mittelständische Unternehmen sind hingegen noch wenig erschlossen in Sachen Process Mining, wobei das nicht ganz richtig ist, denn vieles entwickelt sich – so unsere Erfahrung – aus BI / Data Science Projekten heraus dann doch noch in kleinere Process Mining Applikationen, oft ganz unter dem Radar. In Zukunft – da habe ich keinen Zweifel – wird Process Mining jedoch in jedem Unternehmen mit mehr als 1.000 Mitarbeitern ganz selbstverständlich und quasi nebenbei gemacht werden.

Process Mining Software – Was sagt Gartner?

Ich habe mal die Gartner Charts zu Process Mining Tools von 2023 und 2024 übereinandergelegt und erkenne daraus die folgende Entwicklung:

– Celonis bleibt der Spitzenreiter nach Gartner, gerät jedoch zunehmend unter Druck auf dieser Spitzenposition.

– SAP hatte mit dem Kauf von Signavio vermutlich auf das richtige Pferd gesetzt, die Enterprise-Readiness für SAP-Kunden ist leicht erahnbar.

– Die Software AG ist schon lange mit Process Mining am Start, kann sich in ihrer Positionierung nur leicht verbessern.

– Ähnlich wenig Bewegung bei UiPath, in Sachen Completness of Vision immer noch deutlich hinter der Software AG.

– Interessant ist die Entwicklung des deutschen Anbieters MEHRWERK Process Mining (MPM), bei Completness of Vision verschlechtert, bei Ability to Execute verbessert.

– Der deutsche Anbieter process.science, mit MEHRWERK und dem früheren (von Celonis gekauften) PAFnow mindestens vergleichbar, ist hier noch immer nicht aufgeführt.

– Microsoft Process Mining ist der relative Sieger in Sachen Aufholjagd mit ihrer eigenen Lösung (die zum Teil auf dem eingekauften Tool namens Minit basiert). Process Mining wurde kürzlich in die Power Automate Plattform und in Power BI integriert.

– Fluxicon (Disco) ist vom Chart verschwunden. Das ist schade, vom Tool her recht gut mit dem aufgekauften Minit vergleichbar (reine Desktop-Applikation).

Process Mining Tool im Gartner Magic Quadrant Chart - 2023 vs 2024

Process Mining Tool im Gartner Magic Quadrant Chart – 2023 vs 2024

Auch wenn ich große Ehrfurcht gegenüber Gartner als Quelle habe, bin ich jedoch nicht sicher, wie weit die Datengrundlage für die Feststellung geht. Ich vertraue soweit der Reputation von Gartner, möchte aber als neutraler Process Mining Experte mit Einblick in den deutschen Markt dazu Stellung beziehen.

Process Mining Tools – Unterschiedliche Erfolgsstories

Aber fangen wir erstmal von vorne an, denn Process Mining Tools haben ihre ganz eigene Geschichte und diese zu kennen, hilft bei der Einordnung von Marktbewegungen etwas und mein Process Mining Software Vergleich auf CIO.de von 2019 ist mittlerweile etwas in die Jahre gekommen. Und Unterhaltungswert haben diese Stories auch, beispielsweise wie ganze Gründer und Teams von diesen Software-Anbietern wie Celonis, UiPath (ehemals ProcessGold), PAFnow (jetzt Celonis), Signavio (jetzt SAP) und Minit (jetzt Microsoft) teilweise im Streit auseinandergingen, eigene Process Mining Tools entwickelt und dann wieder Know How verloren oder selbst aufgekauft wurden – Unter Insidern ist der Gesprächsstoff mit Unterhaltungswert sehr groß.

Dabei darf gerne in Erinnerung gerufen werden, dass Process Mining im Kern eine Graphenanalyse ist, die ein Event Log in Graphen umwandelt, Aktivitäten (Events) stellen dabei die Knoten und die Prozesszeiten die Kanten dar, zumindest ist das grundsätzlich so. Es handelt sich dabei also um eine Analysemethodik und nicht um ein Tool. Ein Process Mining Tool nutzt diese Methodik, stellt im Zweifel aber auch nur exakt diese Visualisierung der Prozessgraphen zur Verfügung oder ein ganzes Tool-Werk von der Datenanbindung und -aufbereitung in ein Event Log bis hin zu weiterführenden Analysen in Richtung des BI-Reportings oder der Data Science.

Im Grunde kann man aber folgende große Herkunftskategorien ausmachen:

1. Process Mining Tools, die als pure Process Mining Software gestartet sind

Hierzu gehört Celonis, das drei-köpfige und sehr geschäftstüchtige Gründer-Team, das ich im Jahr 2012 persönlich kennenlernen durfte. Aber Celonis war nicht das erste Process Mining Unternehmen. Es gab noch einige mehr. Hier fällt mir z. B. das kleine und sympathische Unternehmen Fluxicon ein, dass mit seiner Lösung Disco auch heute noch einen leichtfüßigen Einstieg in Process Mining bietet.

2. Process Mining Tools, die eigentlich aus der Prozessmodellierung oder -automatisierung kommen

Einige Software-Anbieter erkannten frühzeitig (oder zumindest rechtzeitig?), dass Process Mining vielleicht nicht das Kerngeschäft, jedoch eine sinnvolle Ergänzung zu ihrem Portfolio an Software für Prozessmodellierung, -dokumentations oder -automatisierung bietet. Hierzu gehört die Software AG, die eigentlich für ihre ARIS-Prozessmodellierung bekannt war. Und hierzu zählt auch Signavio, die ebenfalls ein reines Prozessmodellierungsprogramm waren und von kurzem von SAP aufgekauft wurden. Aber auch das für RPA bekannte Unternehmen UiPath verleibte sich Process Mining durch den Zukauf von ehemals Process Gold.

3. Process Mining Tools, die Business Intelligence Software erweitern

Und dann gibt es noch diejenigen Anbieter, die bestehende BI Tools mit Erweiterungen zum Process Mining Analysewerkzeug machen. Einer der ersten dieser Anbieter war das Unternehmen PAF (Process Analytics Factory) mit dem Power BI Plugin namens PAFnow, welches von Celonis aufgekauft wurde und heute anscheinend (?) nicht mehr weiterentwickelt wird. Das Unternehmen MEHRWERK, eigentlich ein BI-Dienstleister mit Fokus auf QlikTech-Produkte, bietet für das BI-Tool Qlik Sense ebenfalls eine Erweiterung für Process Mining an und das Unternehmen mit dem unscheinbaren Namen process.science bietet Erweiterungen sowohl für Power BI als auch für Qlik Sense, zukünftig ist eine Erweiterung für Tableu geplant. Process.science fehlt im Gartner Magic Quadrant bis jetzt leider gänzlich, trotz bestehender Marktrelevanz (nach meiner Beobachtung).

Process Mining Tools in der Praxis – Ein Einblick

DAX-Konzerne setzen vor allem auf Celonis. Das Gründer-Team, das starke Vertriebsteam und die Medienpräsenz erst als Unicorn, dann als Decacorn, haben die Türen zu Vorstandsetagen zumindest im mitteleuropäischen Raum geöffnet. Und ganz ehrlich: Dass Celonis ein deutsches Decacorn ist, ist einfach wunderbar. Es ist das erste Decacorn aus Deutschland, das zurzeit wertvollste StartUp in Deutschland und wir können – für den Standort Deutschland – nur hoffen, dass dieser Erfolg bleibt.

Doch wie weit vorne ist Process Mining mit Celonis nun wirklich im Praxiseinsatz? Und ist Celonis für jedes Unternehmen der richtige Einstieg in Process Mining?

Celonis unterscheidet sich von den meisten anderen Tools noch dahingehend, dass es versucht, die ganze Kette des Process Minings in einer einzigen und ausschließlichen Cloud-Anwendung in einer Suite bereitzustellen. Während vor zehn Jahren ich für Celonis noch eine Installation erst einer MS SQL Server Datenbank, etwas später dann bevorzugt eine SAP Hana Datenbank auf einem on-prem Server beim Kunden voraussetzend installieren musste, bevor ich dann zur Installation der Celonis ServerAnwendung selbst kam, ist es heute eine 100% externe Cloud-Lösung. Dies hat anfangs für große Widerstände bei einigen Kunden verursacht, die ehrlicherweise heute jedoch kaum noch eine Rolle spielen. Cloud ist heute selbst für viele mitteleuropäische Unternehmen zum Standard geworden und wird kaum noch infrage gestellt. Vielleicht haben wir auch das ein Stück weit Celonis zu verdanken.

Celonis bietet eine bereits sehr umfassende Anbindung von Datenquellen z. B. für SAP oder Oracle ERP an, mit vordefinierten Event Log SQL Skripten für viele Standard-Prozesse, insbesondere Procure-to-Pay und Order-to-Cash. Aber auch andere Prozesse für andere Geschäftsprozesse z. B. von SalesForce CRM sind bereits verfügbar. Celonis ist zudem der erste Anbieter, der diese Prozessaufbereitung und weiterführende Dashboards in einem App-Store anbietet und so zu einer Plattform wird. Hinzu kommen auch die zuvor als Action Engine bezeichnete Prozessautomation, die mit Lösungen wie Power Automate von Microsoft vergleichbar sind.

Celonis schafft es oftmals in größere Konzerne, ist jedoch selten dann das einzige eingesetzte Process Mining Tool. Meine Kunden und Kontakte aus unterschiedlichsten Unternhemen in Deutschland berichten in Sachen Celonis oft von zu hohen Kosten für die Lizensierung und den Betrieb, zu viel Sales im Vergleich zur Leistung sowie von hohen Aufwänden, wenn der Fokus nicht auf Standardprozesse liegt. Demgegenüber steht jedoch die Tatsache, dass Celonis zumindest für die Standardprozesse bereits viel mitbringt und hier definitiv allen anderen Tool-Anbietern voraus ist und den wohl besten Service bietet.

SAP Signavio rückt nach

Mit dem Aufkauf von Signavio von SAP hat sich SAP meiner Meinung nach an eine gute Position katapultiert. Auch wenn ich vor Jahren noch hätte Wetten können, dass Celonis mal von SAP gekauft wird, scheint der Move mit Signavio nicht schlecht zu wirken, denn ich sehe das Tool bei Kunden mit SAP-Liebe bereits erfolgreich im Einsatz. Dabei scheint SAP nicht den Anspruch zu haben, Signavio zur Plattform für Analytics ausbauen zu wollen, um 1:1 mit Celonis gleichzuziehen, so ist dies ja auch nicht notwendig, wenn Signavio mit SAP Hana und der SAP Datasphere Cloud besser integriert werden wird.

Unternehmen, die am liebsten nur Software von SAP einsetzen, werden also mittlerweile bedient.

Mircosoft holt bei Process Mining auf

Ein absoluter Newcomer unter den Großen Anbietern im praktischen Einsatz bei Unternehmen ist sicherlich Microsoft Process Mining. Ich betreue bereits selbst Kunden, die auf Microsoft setzen und beobachte in meinem Netzwerk ein hohes Interesse an der Lösung von Microsoft. Was als logischer Schritt von Microsoft betrachtet werden kann, ist in der Praxis jedoch noch etwas hakelig, da Microsoft – und ich weiß wovon ich spreche – aktuell noch ein recht komplexes Zusammenspiel aus dem eigentlichen Process Mining Client (ehemals Minit) und der Power Automate Plattform sowie Power BI bereitstellt. Sehr hilfreich ist die Weiterführung der Process Mining Analyse vom Client-Tool dann direkt in der PowerBI Cloud. Das Ganze hat definitiv Potenzial, hängt aber in Details in 2024 noch etwas in diesem Zusammenspiel an verschiedenen Tools, die kein einfaches Setup für den User darstellen.

Doch wenn diese Integration besser funktioniert, und das ist in Kürze zu erwarten, dann bringt das viele Anbieter definitiv in Bedrängnis, denn den Microsoft Stack nutzen die meisten Unternehmen sowieso. Somit wäre kein weiteres Tool für datengetriebene Prozessanalysen mehr notwendig.

Process Mining – Und wie steht es um Machine Learning?

Obwohl ich mich gemeinsam mit Kunden besonders viel mit Machine Learning befasse, sind die Beispiele mit Process Mining noch recht dünn gesäht, dennoch gibt es etwa seit 2020 in Sachen Machine Learning für Process Mining auch etwas zu vermelden.

Celonis versucht Machine Learning innerhalb der Plattform aus einer Hand anzubieten und hat auch eigene Python-Bibleotheken dafür entwickelt. Bisher dreht sich hier viel eher noch um z. B. die Vorhersage von Prozesszeiten oder um die Erkennung von Doppelvorgängen. Die Erkennung von Doppelzahlungen ist sogar eine der penetrantesten Werbeversprechen von Celonis, obwohl eigentlich bereits mit viel einfacherer Analytik effektiv zu bewerkstelligen.

Von Kunden bisher über meinen Geschäftskanal nachgefragte und umgesetzte Machine Learning Funktionen sind u.a. die Anomalie-Erkennung in Prozessdaten, die möglichst frühe Vorhersage von Prozesszeiten (oder -kosten) und die Impact-Prediction auf den Prozess, wenn ein bestimmtes Event eintritt.

Umgesetzt werden diese Anwendungsfälle bisher vor allem auf dritten Plattformen, wie z. B. auf den Analyse-Ressourcen der Microsoft Azure Cloud oder in auf der databricks-Plattform.

Während das nun Anwendungsfälle auf der Prozessanalyse-Seite sind, kann Machine Learning jedoch auf der anderen Seite zur Anwendung kommen: Mit NER-Verfahren (Named Entity Recognition) aus dem NLP-Baukasten (Natural Language Processing) können Event Logs aus unstrukturierten Daten gewonnen werden, z. B. aus Texten in E-Mails oder Tickets.

Data Lakehouse – Event Logs außerhalb des Process Mining Tools

Auch wenn die vorbereitete Anbindung von Standard-ERP-Systemen und deren Standard-Prozesse durch Celonis einen echten Startvorteil bietet, so schwenken Unternehmen immer mehr auf die Etablierung eines unternehmensinternen Data Warehousing oder Data Lakehousing Prozesses, der die Daten als “Data Middlelayer” vorhält und Process Mining Applikationen bereitstellt.

Ich selbst habe diese Beobachtung bereits bei Unternehmen der industriellen Produktion, Handel, Finanzdienstleister und Telekommunikation gemacht und teilweise selbst diese Projekte betreut und/oder umgesetzt. Recht unterschiedlich hingegen ist die interne Benennung dieser Architektur, von “Middlelayer” über “Data Lakehouse” oder “Event Log Layer” bis “Data Hub” waren sehr unterschiedliche Bezeichnungen dabei. Gemeinsam haben sie alle die Funktion als Zwischenebene zwischen den Datenquellen und den Process Mining, BI und Data Science Applikationen.

DATANOMIQ Cloud Architecture for Data Mesh - Process Mining, BI and Data Science Applications

Prinzipielle Architektur-Darstellung eines Data Lakehouse Systems unter Einsatz von Databricks auf der Goolge / Amazon / Microsoft Azure Cloud nach dem Data Mesh Konzept zur Bereitstellung von Data Products für Process Mining, BI und Data Science Applikationen. Alternativ zu Databricks können auch andere Data Warehouse Datenbankplattformen zur Anwendung kommen, beispielsweise auch snowflake mit dbt.

Das Kernziel der Zwischenschicht erstellt für die Process Mining Vohaben die benötigten Event Logs, kann jedoch diesselben Daten für ganz andere Vorhaben und Applikationen zur Verfügung zu stellen.

Vorteile des Data Lakehousing

Die Vorteile einer Daten-Zwischenschicht in Form eines Data Warehouses oder Data Lakehouses sind – je nach unternehmensinterner Ausrichtung – beispielsweise die folgenden:

  • Keine doppelte Datenhaltung, denn Daten können zentral gehalten werden und in Views speziellen Applikationen der BI, Data Science, KI und natürlich auch für Process Mining genutzt werden.
  • Einfachere Data Governance, denn eine zentrale Datenschicht zwischen den Applikationen erleichtert die Übersicht und die Aussteuerung der Datenzugriffsberechtigung.
  • Reduzierte Cloud Kosten, denn Cloud Tools berechnen Gebühren für die Speicherung von Daten. Müssen Rohdatentabellen in die Analyse-Tools wie z. B. Celonis geladen werden, kann dies unnötig hohe Kosten verursachen.
  • Reduzierte Personalkosten, sind oft dann gegeben, wenn interne Data Engineers verfügbar sind, die die Datenmodelle intern entwickeln.
  • Höhere Data Readiness, denn für eine zentrale Datenplattform lohn es sich eher, Daten aus weniger genutzten Quellen anzuschließen. Hier ergeben sich oft neue Chancen der Datenfusion für nützliche Analysen, die vorher nicht angedacht waren, weil sich der Aufwand nur hierfür speziell nicht lohne.
  • Große Datenmodelle werden möglich und das Investment in diese lohnt sich nun, da sie für verschiedene Process Mining Tools ausgeliefert werden können, oder auch nur Sichten (Views) auf Prozess-Perspektiven. So wird Object-centric Process Mining annäherend mit jedem Tool möglich.
  • Nutzung von heterogenen Datenquellen, denn mit einem Data Lakehouse ist auch die Nutzung von unstrukturierten Daten leicht möglich, davon wird in Zukunft auch Process Mining profitieren. Denn dank KI und NLP (Data Science) können auch Event Logs aus unstrukturierten Daten generiert werden.
  • Unabhängigkeit von Tool-Anbietern, denn wenn die zentrale Datenschicht die Daten in Datenmodelle aufbereitet (im Falle von Process Mining oft in normalisierten Event Logs), können diese allen Tools zur Verfügung gestellt werden. Dies sorgt für Unabhängigkeit gegenüber einzelnen Tool-Anbietern.
  • Data Science und KI wird erleichtert, denn die Data Science und das Training im Machine Learning kann direkt mit dem reichhaltigen Pool an Daten erfolgen, auch direkt mit den Daten der Event Logs und losgelöst vom Process Mining Analyse-Tool, z. B. in Databricks oder den KI-Tools von Google, AWS und Mircosoft Azure (Azure Cognitive Services, Azure Machine Learning etc.).

Unter diesen Aspekten wird die Tool-Auswahl für die Prozessanalyse selbst in ihrer Relevanz abgemildert, da diese Tools schneller ausgetauscht werden können. Dies könnte auch bedeuten, dass sich für Unternehmen die Lösung von Microsoft besonders anbietet, da das Data Engineering und die Data Science sowieso über andere Cloud Services abgebildet wird, jedoch kein weiterer Tool-Anbieter eingebunden werden muss.

Process Mining / Process Analytics

Process Mining Software – Fazit

Es ist viel Bewegung am Markt und bietet dem Beobachter auch tatsächlich etwas Entertainment. Celonis ist weiterhin der Platzhirsch und wir können sehr froh sein, dass wir es hier mit einem deutschen Start-Up zutun haben. Für Unternehmen, die gleich voll in Process Mining reinsteigen möchten und keine Scheu vor einem möglichen Vendor-Lock-In, bietet Celonis meiner Ansicht nach immer noch das beste Angebot, wenn auch nicht die günstigste Lösung. Die anderen Tools können ebenfalls eine passende Lösung sein, nicht nur aus preislichen Gründen, sondern vor allem im Kontext der zu untersuchenden Prozesse, der Datenquellen und der bestehenden Tool-Landschaft. Dies sollte im Einzelfall geprüft werden.

Die Datenbereitstellung und -aufbereitung sollte idealerweise nicht im Process Mining Tool erfolgen, sondern auf einer zentralen Datenschicht als Data Warehouse oder Data Lakehouse für Process Mining. Die damit gewonnene Data Readiness zahlt nicht nur auf datengetriebene Prozessanalysen ein, sondern kommt dem ganzen Unternehmen zu Gute und ermöglicht zukünftige Projekte mit Daten, an die vorher oder bisher gar nicht zu denken waren.

Dieser Artikel wurde von Benjamin Aunkofer, einem neutralen Process Mining Berater, ohne KI (ohne ChatGPT etc.) verfasst!
Continuous Integration and Continuous Delivery (CI/CD) for Data Pipelines
Benjamin Aunkofer

CI/CD für Datenpipelines – Ein Game-Changer mit AnalyticsCreator

/in , , , /by

Continuous Integration und Continuous Delivery (CI/CD) für Datenpipelines: Ein Game-Changer mit AnalyticsCreator!

Die Bedeutung effizienter und zuverlässiger Datenpipelines in den Bereichen Data Science und Data Engineering ist enorm. CI/CD, als Teil von DevOps, unterstützt Softwareentwicklungsteams dabei, Codeänderungen häufiger und zuverlässiger bereitzustellen. Dieser Ansatz ermöglicht es Entwicklern, an einem gemeinsamen Code-Repository zu arbeiten, automatisierte Buildprozesse zu nutzen und so einen schnelleren Entwicklungszyklus mit geringerer Fehlerquote zu erreichen.

Einsatz von CI/CD in Datenpipelines

Datenpipelines fördern Konsistenz, reduzieren Fehler und steigern die Effizienz, indem sie Daten in ein nutzbares Format umwandeln. Automatisierung hilft dabei, menschliche Fehler zu vermeiden und ermöglicht es Datenexperten, sich auf das Wesentliche zu konzentrieren: das Gewinnen von Erkenntnissen und die Unterstützung von Unternehmen bei der Entscheidungsfindung.

Die Rolle von AnalyticsCreator

AnalyticsCreator erweist sich als leistungsstarkes Werkzeug zur Steigerung von Effizienz und Zuverlässigkeit in CI/CD-Prozessen. Es bietet vollständige Automatisierung des BI-Stacks und unterstützt ein breites Spektrum an Data Warehouses, analytischen Datenbanken und Frontends.

Hauptmerkmale von AnalyticsCreator:

  • Ganzheitliches Datenmodell: Ermöglicht schnelles Prototyping verschiedener Datenmodelle.
  • Automatisierung: Erstellt SQL-Code, DACPAC-Dateien, SSIS-Pakete, Data Factory-ARM-Vorlagen und XMLA-Dateien.
  • Vielfältige Unterstützung: Kompatibel mit verschiedenen Datenbankmanagementsystemen wie MS SQL Server und Azure Synapse Analytics.
  • Data Lakes: Unterstützt MS Azure Blob Storage.
  • Frontends: Kompatibel mit Tools wie Power BI, Qlik Sense und Tableau.
  • Pipelines/ETL: Unterstützt Technologien wie SQL Server Integration Services und Azure Data Factory.
  • Bereitstellungsoptionen: Bietet verschiedene Methoden zur Bereitstellung und Verwaltung von Datenpipelines.
  • Modellierungsansätze: Unterstützt diverse Modellierungsmethoden, einschließlich Dimensional/Kimball und Data Vault 2.0.

Versionierung: Ermöglicht die Nachverfolgung von Änderungen und die Sicherstellung der Data Governance.

Schlussfolgerung

Die Integration von CI/CD in Datenpipelines, verstärkt durch die Fähigkeiten von AnalyticsCreator, kann die Effizienz und Zuverlässigkeit im Datenmanagement signifikant erhöhen. Dies führt zu schnelleren und verlässlicheren Updates und stellt eine wesentliche Verbesserung im Bereich der Datenwi

Continuous Integration and Continuous Delivery (CI/CD) for Data Pipelines
Benjamin Aunkofer

CI/CD for Data Pipelines: A Game-Changer with AnalyticsCreator

/in , /by

Continuous Integration and Continuous Delivery (CI/CD) for Data Pipelines: It is a Game-Changer with AnalyticsCreator!

The need for efficient and reliable data pipelines is paramount in data science and data engineering. This is where Continuous Integration and Continuous Delivery (CI/CD) come into play. CI/CD, a set of processes that help software development teams deliver code changes more frequently and reliably, is part of DevOps. It’s a software development approach where all developers work together on a shared repository of code. As changes are made, there are automated build processes for detecting code issues. The outcome is a faster development life cycle and a lower error rate.

CI/CD for Data Pipelines

Data pipelines provide consistency, reduce errors, and increase efficiency. They transform data into a consistent format for users to consume. Automated data pipelines eliminate human errors when manipulating data. Data professionals save time spent on data processing transformation. Saving time allows them to focus on their core job function – getting the insight out of the data and helping businesses make better decisions.

Enter AnalyticsCreator

AnalyticsCreator, a powerful tool for data management, brings a new level of efficiency and reliability to the CI/CD process. It offers full BI-Stack Automation, from source to data warehouse through to frontend. It supports a holistic data model, allowing for rapid prototyping of various models. It also supports a wide range of data warehouses, analytical databases, data lakes, frontends, and pipelines/ETL.

Key Features of AnalyticsCreator

  1. Holistic Data Model: AnalyticsCreator provides a complete view of the entire Data Model. This allows for rapid prototyping of various models.
  2. Automation: It offers full BI-Stack Automation, from source to data warehouse through to frontend. This includes the creation of SQL Code, DACPAC files, SSIS packages, Data Factory ARM templates, and XMLA files.
  3. Support for Various Data Warehouses and Databases: AnalyticsCreator supports MS SQL Server 2012-2022, Azure SQL Database, Azure Synapse Analytics dedicated, and more.
  4. Data Lakes: It supports MS Azure Blob Storage.
  5. Frontends: AnalyticsCreator supports Power BI, Qlik Sense, Tableau, PowerPivot (Excel).
  6. Pipelines/ETL: It supports SQL Server Integration Packages (SSIS), Azure Data Factory 2.0 pipelines, Azure Data Bricks.
  7. Deployment: AnalyticsCreator supports deployment through Visual Studio Solution (SSDT), Creation of DACPAC files, SSIS packages, Data Factory ARM templates, XMLA files.
  8. Modelling Approaches: It supports top-down modelling, bottom-up modelling, import from external modelling tool, Dimensional/Kimball, Data Vault 2.0, Mixed approach of DV 2.0 and Kimball, Inmon, 3NF, or any custom data model.
  9. Versioning: AnalyticsCreator maintains a version of history of metadata changes. Collaborators can track modifications, revert to presivous versions, and ensure data governance.

Conclusion

The integration of CI/CD in data pipelines, coupled with the power of AnalyticsCreator, can significantly enhance the efficiency and reliability of data management. It not only automates the testing, deployment, and monitoring of data pipelines but also ensures faster and more reliable updates.  This is indeed a game-changer in the realm of data science.

Benjamin Aunkofer über Karriere mit Daten, Datenkompetenz und Datenstrategie
Redaktion

Data Jobs – Podcast-Folge mit Benjamin Aunkofer

/in , , , , , , , , , /by

In der heutigen Geschäftswelt ist der Einsatz von Daten unerlässlich, insbesondere für Unternehmen mit über 100 Mitarbeitern, die erfolgreich bleiben möchten. In der Podcast-Episode “Data Jobs – Was brauchst Du, um im Datenbereich richtig Karriere zu machen?” diskutieren Dr. Christian Krug und Benjamin Aunkofer, Gründer von DATANOMIQ, wie Angestellte ihre Datenkenntnisse verbessern und damit ihre berufliche Laufbahn aktiv vorantreiben können. Dies steigert nicht nur ihren persönlichen Erfolg, sondern erhöht auch den Nutzen und die Wettbewerbsfähigkeit des Unternehmens. Datenkompetenz ist demnach ein wesentlicher Faktor für den Erfolg sowohl auf individueller als auch auf Unternehmensebene.

In dem Interview erläutert Benjamin Aunkofer, wie man den Einstieg auch als Quereinsteiger schafft. Das Sprichwort „Ohne Fleiß kein Preis“ trifft besonders auf die Entwicklung beruflicher Fähigkeiten zu, insbesondere im Bereich der Datenverarbeitung und -analyse. Anstelle den Abend mit Serien auf Netflix zu verbringen, könnte man die Zeit nutzen, um sich durch Fachliteratur weiterzubilden. Es gibt eine Vielzahl von Büchern zu Themen wie Data Science, Künstliche Intelligenz, Process Mining oder Datenstrategie, die wertvolle Einblicke und Kenntnisse bieten können.

Der Nutzen steht in einem guten Verhältnis zum Aufwand, so Benjamin Aunkofer. Für diejenigen, die wirklich daran interessiert sind, in eine Datenkarriere einzusteigen, stehen die Türen offen. Der Einstieg erfordert zwar Engagement und Lernbereitschaft, ist aber für entschlossene Individuen absolut machbar. Dabei muss man nicht unbedingt eine Laufbahn als Data Scientist anstreben. Jede Fachkraft und insbesondere Führungskräfte können erheblich davon profitieren, die Grundlagen von Data Engineering und Data Science zu verstehen. Diese Kenntnisse ermöglichen es, fundiertere Entscheidungen zu treffen und die Potenziale der Datenanalyse optimal für das Unternehmen zu nutzen.

Podcast-Folge mit Benjamin Aunkofer und Dr. Christian Krug darüber, wie Menschen mit Daten Karriere machen und den Unternehmenserfolg herstellen!

Podcast-Folge mit Benjamin Aunkofer und Dr. Christian Krug darüber, wie Menschen mit Daten Karriere machen und den Unternehmenserfolg herstellen.

 

Zur Podcast-Folge auf Spotify: https://open.spotify.com/show/6Ow7ySMbgnir27etMYkpxT?si=dc0fd2b3c6454bfa

Zur Podcast-Folge auf iTunes: https://podcasts.apple.com/de/podcast/unf-ck-your-data/id1673832019

Zur Podcast-Folge auf Google: https://podcasts.google.com/feed/aHR0cHM6Ly9mZWVkcy5jYXB0aXZhdGUuZm0vdW5mY2steW91ci1kYXRhLw?ep=14

Zur Podcast-Folge auf Deezer: https://deezer.page.link/FnT5kRSjf2k54iib6

Redaktion

Machine Learning in Data Science (berufsbegleitendes, weiterbildendes Studium der TU Dortmund)

/in , , , /by
Anzeige

Die Technische Universität Dortmund bietet im Herbst 2024 das neue weiterbildende Studium ‚Machine Learning in Data Science‘ an. Der Kurs findet berufsbegleitend statt. Angesprochen sind Fach- und Führungskräfte, die in ihrem beruflichen Alltag mit Datenmengen zu tun haben und die ihre Kompetenzen im Bereich statistische Methoden und maschinellem Lernen ausbauen möchten (z. B. Data- und Business-Analyst*innen, Wissenschaftler*innen, Softwareentwickler*innen, Berater*innen, Data Scientists, Ingenieur*innen und andere interessierte Berufsbilder).

 

Zahlen – Daten – Fakten

Start: 26.09.2024

Anmeldeschluss: 23.08.2024

Ende: ca. September 2025

Zeitlicher Umfang: 10 Seminartage und 1 Prüfungstag sowie Anwendungsaufgaben

Abschluss: Universitätszertifikat (nach §62 Hochschulgesetz NRW) mit einem Umfang von 10 ECTS

Kosten: 4.900 € (zahlbar in 3 Raten)

 

Machine Learning in Data Science @ TU Dortmund

Machine Learning in Data Science @ TU Dortmund

 

Ziel ist des Kurses…

…ist der Erwerb von Wissen und Fertigkeiten zu Datenmanagement und –exploration, maschinellem Lernen und statistischen Methoden, im diese im Berufsalltag zur Analyse und Interpretation von Daten anwenden zu können.

 

Warum lohnt sich eine Teilnahme am Kurs für Teilnehmende aus Wirtschaft, Industrie, Wissenschaft und öffentlichem Dienst?

  • Nachweisbarer Kompetenzuwachs: Erwerb eines Universitätszertifikats
  • ‚bring your own data‘: eine konkrete Fragestellung aus dem Berufsalltag kann im Rahmen der Abschlussarbeit bearbeitet werden – so wird Gelerntes direkt in der Praxis angewendet und kann einen Mehrwert für das Unternehmen haben
  • Strukturierter Wissenserwerb in 2 Stufen: Verstehen und Erklären von Methoden in der ersten Stufe, praktische Anwendung in der zweiten Stufe (durch z. B. Analyse von realen Datensätzen)

Weitersagen lohnt sich!

Wenn Sie gemeinsam mit einer/einem Kollegin/Kollegen oder mehreren Personen aus Ihrem Unternehmen am Kurs teilnehmen, reduziert sich das Teilnahmeentgelt bei bis zu zwei angemeldeten Personen um 5 % pro Person, darüber hinausgehend zahlt jede weitere Person 10 % weniger.

Vertiefende Informationen zum Kurs finden Sie unter: https://wb.zhb.tu-dortmund.de/mlds

Ansprechpartner für Rückfragen: Daniel Neubauer, daniel.neubauer@tu-dortmund.de, 0231 755 6632

Folgen Sie gerne die LinkedIn-Seite der Weiterbildung für Data Science und Machine Learning der TU Dortmund: https://www.linkedin.com/company/tu-do-mlds/

Benjamin Aunkofer im Interview mit Atreus Interim Management über Daten & KI in Unternehmen
Redaktion

Video Interview – Interim Management für Daten & KI

/in /by

Data & AI im Unternehmen zu etablieren ist ein Prozess, der eine fachlich kompetente Führung benötigt. Hier kann Interim Management die Lösung sein.

Unternehmer stehen dabei vor großen Herausforderungen und stellen sich oft diese oder ähnliche Fragen:

  • Welche Top-Level Strategie brauche ich?
  • Wo und wie finde ich die ersten Show Cases im Unternehmen?
  • Habe ich aktuell den richtigen Daten back-bone?

Diese Fragen beantwortet Benjamin Aunkofer (Gründer von DATANOMIQ und AUDAVIS) im Interview mit Atreus Interim Management. Er erläutert, wie Unternehmen die Disziplinen Data Science, Business Intelligence, Process Mining und KI zusammenführen können, und warum Interim Management dazu eine gute Idee sein kann.

Video Interview “Meet the Manager” auf Youtube mit Franz Kubbillum von Atreus Interim Management und Benjamin Aunkofer von DATANOMIQ.

Über Benjamin Aunkofer

Benjamin Aunkofer - Interim Manager für Data & AI, Gründer von DATANOMIQ und AUDAVIS.

Benjamin Aunkofer – Interim Manager für Data & AI, Gründer von DATANOMIQ und AUDAVIS.

Benjamin Aunkofer ist Gründer des Beratungs- und Implementierungspartners für Daten- und KI-Lösungen namens DATANOMIQ sowie Co-Gründer der AUDAVIS, einem AI as a Service für die Wirtschaftsprüfung.

Nach seiner Ausbildung zum Software-Entwickler (FI-AE IHK) und seinem Einstieg als Consultant bei Deloitte, gründete er 2015 die DATANOMIQ GmbH in Berlin und unterstütze mit mehreren kleinen Teams Unternehmen aus unterschiedlichen Branchen wie Handel, eCommerce, Finanzdienstleistungen und der produzierenden Industrie (Pharma, Automobilzulieferer, Maschinenbau). Er partnert mit anderen Unternehmensberatungen und unterstütze als externer Dienstleister auch Wirtschaftsprüfungsgesellschaften.

Der Projekteinstieg in Unternehmen erfolgte entweder rein projekt-basiert (Projektangebot) oder über ein Interim Management z. B. als Head of Data & AI, Chief Data Scientist oder Head of Process Mining.

Im Jahr 2023 gründete Benjamin Aunkofer mit zwei Mitgründern die AUDAVIS GmbH, die eine Software as a Service Cloud-Plattform bietet für Wirtschaftsprüfungsgesellschaften, Interne Revisionen von Konzernen oder für staatliche Prüfung von Finanztransaktionen.

 

Datenbusiness
Redaktion

Data Unplugged – Event Empfehlung

/in , /by

Mit der Anwesenheit von bis zu 1000 Data and AI Enthusiasts, wird die data:unplugged Veranstaltung eines der größten Data und KI Events des Jahres sein. Mit einer erstklassigen Mischung aus fachlichem Austausch, inspirierenden Reden, Music Acts verschiedener Genres, Comedy und einem kulinarischen Angebot, zelebrieren wir alle gemeinsam KI.

Jetzt noch schnell ein Data Unplugged Ticket kaufen und dabei sein!

Data Unplugged Event in Münster

Data Unplugged Event in Münster

Die Veranstaltung in Münster bietet umfangreiche Themen, ist nicht zu technisch, sondern versucht die Seite des unternehmerischen und gesellschaftlichen Nutzen von Daten und KI zu beleuchten.

Daten-Ethik

Ethische Überlegungen sind entscheidend für die Entwicklung und den Einsatz der KI-Technologie. Deshalb haben wir einen bedeutenden Teil der Veranstaltung der Erforschung der ethischen Auswirkungen von KI gewidmet und wie diese angegangen werden können.

Data Leadership

Unsere Hauptredner:innen und Workshop-Leiter:innen werden anregende Einblicke und praktische Anleitungen bieten, wie man KI-Systeme entwickeln und einsetzen kann, die verantwortungsbewusst, transparent und im Einklang mit menschlichen Werten stehen.

Data Innovation

Data Unplugged wird die neuesten Fortschritte in der KI und ihr potenzielles Auswirkungspotenzial auf Unternehmen, Branchen und die Gesellschaft hervorheben. Die Teilnehmer:innen werden über die neuesten Trends in der KI-Entwicklung erfahren und wie sie diese Trends nutzen können, um Innovationen in ihren eigenen Organisationen voranzutreiben.

Die Raumzeit der Veranstaltung

Die Veranstaltung Data::Unplugged findet am 07.03.2024 im Skaters Palace in Münster statt. Tickets sind über diesen Link (Klick) erhältlich.

Der Organisator

Organisiert wird das Data Unplugged Event von Datenbusiness.de. Mit mehreren 10.000 Data Experts bietet Datenbusiness.de die Deutschlands führende Data & AI Community.

Datenbusiness.de

 

Der bekannteste Kanal dieser Community ist der Datenbusiness Podcast. Jetzt reinhören direkt auf Datenbusiness.de oder via:

Object-centric Data Modelling for Process Mining and BI
Benjamin Aunkofer

Object-centric Process Mining on Data Mesh Architectures

/in , , , , , , , , , , , , , /by

In addition to Business Intelligence (BI), Process Mining is no longer a new phenomenon, but almost all larger companies are conducting this data-driven process analysis in their organization.

The database for Process Mining is also establishing itself as an important hub for Data Science and AI applications, as process traces are very granular and informative about what is really going on in the business processes.

The trend towards powerful in-house cloud platforms for data and analysis ensures that large volumes of data can increasingly be stored and used flexibly. This aspect can be applied well to Process Mining, hand in hand with BI and AI.

New big data architectures and, above all, data sharing concepts such as Data Mesh are ideal for creating a common database for many data products and applications.

The Event Log Data Model for Process Mining

Process Mining as an analytical system can very well be imagined as an iceberg. The tip of the iceberg, which is visible above the surface of the water, is the actual visual process analysis. In essence, a graph analysis that displays the process flow as a flow chart. This is where the processes are filtered and analyzed.

The lower part of the iceberg is barely visible to the normal analyst on the tool interface, but is essential for implementation and success: this is the Event Log as the data basis for graph and data analysis in Process Mining. The creation of this data model requires the data connection to the source system (e.g. SAP ERP), the extraction of the data and, above all, the data modeling for the event log.

Simple Data Model for a Process Mining Event Log

Simple Data Model for a Process Mining Event Log.

As part of data engineering, the data traces that indicate process activities are brought into a log-like schema. A simple event log is therefore a simple table with the minimum requirement of a process number (case ID), a time stamp and an activity description.

Event Log in Process Mining

Example Event Log for Process Mining

An Event Log can be seen as one big data table containing all the process information. Splitting this big table into several data tables is due to the goal of increasing the efficiency of storing the data in a normalized database.

The following example SQL-query is inserting Event-Activities from a SAP ERP System into an existing event log database table (one big table). It shows that events are based on timestamps (CPUDT, CPUTM) and refer each to one of a list of possible activities (dependent on VGABE).

Attention: Please see this SQL as a pure example of event mining for a classic (single table) event log! It is based on a German SAP ERP configuration with customized processes.

An Event Log can also include many other columns (attributes) that describe the respective process activity in more detail or the higher-level process context.

Incidentally, Process Mining can also work with more than just one timestamp per activity. Even the small Process Mining tool Fluxicon Disco made it possible to handle two activities from the outset. For example, when creating an order in the ERP system, the opening and closing of an input screen could be recorded as a timestamp and the execution time of the micro-task analyzed. This concept is continued as so-called task mining.

Task Mining

Task Mining is a subtype of Process Mining and can utilize user interaction data, which includes keystrokes, mouse clicks or data input on a computer. It can also include user recordings and screenshots with different timestamp intervals.

As Task Mining provides a clearer insight into specific sub-processes, program managers and HR managers can also understand which parts of the process can be automated through tools such as RPA. So whenever you hear that Process Mining can prepare RPA definitions you can expect that Task Mining is the real deal.

Machine Learning for Process and Task Mining on Text and Video Data

Process Mining and Task Mining is already benefiting a lot from Text Recognition (Named-Entity Recognition, NER) by Natural Lamguage Processing (NLP) by identifying events of processes e.g. in text of tickets or e-mails. And even more Task Mining will benefit form Computer Vision since videos of manufacturing processes or traffic situations can be read out. Even MTM analysis can be done with Computer Vision which detects movement and actions in video material.

Object-Centric Process Mining

Object-centric Process Data Modeling is an advanced approach of dynamic data modelling for analyzing complex business processes, especially those involving multiple interconnected entities. Unlike classical process mining, which focuses on linear sequences of activities of a specific process chain, object-centric process mining delves into the intricacies of how different entities, such as orders, items, and invoices, interact with each other. This method is particularly effective in capturing the complexities and many-to-many relationships inherent in modern business processes.

Note from the author: The concept and name of object-centric process mining was introduced by Wil M.P. van der Aalst 2019 and as a product feature term by Celonis in 2022 and is used extensively in marketing. This concept is based on dynamic data modelling. I probably developed my first event log made of dynamic data models back in 2016 and used it for an industrial customer. At that time, I couldn’t use the Celonis tool for this because you could only model very dedicated event logs for Celonis and the tool couldn’t remap the attributes of the event log while on the other hand a tool like Fluxicon disco could easily handle all kinds of attributes in an event log and allowed switching the event perspective e.g. from sales order number to material number or production order number easily.

An object-centric data model is a big deal because it offers the opportunity for a holistic approach and as a database a single source of truth for Process Mining but also for other types of analytical applications.

Enhancement of the Data Model for Obect-Centricity

The Event Log is a data model that stores events and their related attributes. A classic Event Log has next to the Case ID, the timestamp and a activity description also process related attributes containing information e.g. about material, department, user, amounts, units, prices, currencies, volume, volume classes and much much more. This is something we can literally objectify!

The problem of this classic event log approach is that this information is transformed and joined to the Event Log specific to the process it is designed for.

An object-centric event log is a central data store for all kind of events mapped to all relevant objects to these events. For that reason our event log – that brings object into the center of gravity – we need a relational bridge table (Event_Object_Relation) into the focus. This tables creates the n to m relation between events (with their timestamps and other event-specific values) and all objects.

For fulfillment of relational database normalization the object table contains the object attributes only but relates their object attribut values from another table to these objects.

Advanced Event Log with dynamic Relations between Objects and Events

Advanced Event Log with dynamic Relations between Objects and Events

The above showed data model is already object-centric but still can become more dynamic in order to object attributes by object type (e.g. the type material will have different attributes then the type invoice or department). Furthermore the problem that not just events and their activities have timestamps but also objects can have specific timestamps (e.g. deadline or resignation dates).

Advanced Event Log with dynamic Relations between Objects and Events and dynamic bounded attributes and their values to Events - And the same for Objects.

Advanced Event Log with dynamic Relations between Objects and Events and dynamic bounded attributes and their values to Events – And the same for Objects.

A last step makes the event log data model more easy to analyze with BI tools: Adding a classical time dimension adding information about each timestamp (by date, not by time of day), e.g. weekdays or public holidays.

Advanced Event Log with dynamic Relations between Objects and Events and dynamic bounded attributes and their values to Events and Objects. The measured timestamps (and duration times in case of Task Mining) are enhanced with a time-dimension for BI applications.

Advanced Event Log with dynamic Relations between Objects and Events and dynamic bounded attributes and their values to Events and Objects. The measured timestamps (and duration times in case of Task Mining) are enhanced with a time-dimension for BI applications.

For analysis the way of Business Intelligence this normalized data model can already be used. On the other hand it is also possible to transform it into a fact-dimensional data model like the star schema (Kimball approach). Also Data Science related use cases will find granular data e.g. for training a regression model for predicting duration times by process.

Note from the author: Process Mining is often regarded as a separate discipline of analysis and this is a justified classification, as process mining is essentially a graph analysis based on the event log. Nevertheless, process mining can be considered a sub-discipline of business intelligence. It is therefore hardly surprising that some process mining tools are actually just a plugin for Power BI, Tableau or Qlik.

Storing the Object-Centrc Analytical Data Model on Data Mesh Architecture

Central data models, particularly when used in a Data Mesh in the Enterprise Cloud, are highly beneficial for Process Mining, Business Intelligence, Data Science, and AI Training. They offer consistency and standardization across data structures, improving data accuracy and integrity. This centralized approach streamlines data governance and management, enhancing efficiency. The scalability and flexibility provided by data mesh architectures on the cloud are very beneficial for handling large datasets useful for all analytical applications.

Note from the author: Process Mining data models are very similar to normalized data models for BI reporting according to Bill Inmon (as a counterpart to Ralph Kimball), but are much more granular. While classic BI is satisfied with the header and item data of orders, process mining also requires all changes to these orders. Process mining therefore exceeds this data requirement. Furthermore, process mining is complementary to data science, for example the prediction of process runtimes or failures. It is therefore all the more important that these efforts in this treasure trove of data are centrally available to the company.

Central single source of truth models also foster collaboration, providing a common data language for cross-functional teams and reducing redundancy, leading to cost savings. They enable quicker data processing and decision-making, support advanced analytics and AI with standardized data formats, and are adaptable to changing business needs.

DATANOMIQ Data Mesh Cloud Architecture - This image is animated! Click to enlarge!

DATANOMIQ Data Mesh Cloud Architecture – This image is animated! Click to enlarge!

 

Central data models in a cloud-based Data Mesh Architecture (e.g. on Microsoft Azure, AWS, Google Cloud Platform or SAP Dataverse) significantly improve data utilization and drive effective business outcomes. And that´s why you should host any object-centric data model not in a dedicated tool for analysis but centralized on a Data Lakehouse System.

About the Process Mining Tool for Object-Centric Process Mining

Celonis is the first tool that can handle object-centric dynamic process mining event logs natively in the event collection. However, it is not neccessary to have Celonis for using object-centric process mining if you have the dynamic data model on your own cloud distributed with the concept of a data mesh. Other tools for process mining such as Signavio, UiPath, and process.science or even the simple desktop tool Fluxicon Disco can be used as well. The important point is that the data mesh approach allows you to easily generate classic event logs for each analysis perspective using the dynamic object-centric data model which can be used for all tools of process visualization…

… and you can also use this central data model to generate data extracts for all other data applications (BI, Data Science, and AI training) as well!

DataScientest.com Weiterbildung zum Data Scientist
Redaktion

Data Scientist Weiterbildung | datascientest.com

/in , , /by
Die Data Science Weiterbildung @ datascientest.com ist eine echte anerkannte berufliche Weiterbildung.
logo sorbonne
Die Zertifizierung wird von der Pariser Universität La Sorbonne ausgestellt.

Während Deiner gesamten Data Scientist-Weiterbildung wirst Du an einem Dataprojekt mit einem Umfang von 120 Stunden arbeiten. Ziel ist es, das Gelernte in einem konkreten Bereich anzuwenden und eine erste praktische Erfahrung zu sammeln. Die Zertifizierung wird von der Pariser Universität La Sorbonne ausgestellt.

Data Scientist Weiterbildung

Als Bootcamp (3 Monate) oder in Teilzeit​ (9 Monate).
Die Kurse starten jeden Monat!

Sichere Dir einen anerkannten Abschluss und erhalte Karriereunterstützung bis Du Deinen Traumjob als Data Scientist findest!

Diese Weiterbildung beinhaltet eine Vorbereitung zum Erhalt der AWS-Zertifizierung Cloud Practitioner.
Weitere Informationen gewünscht? Einfach hier downloaden!

 

Hybride Lernformat

Die Kombination aus der interaktiven Lernplattform und von erfahrenen Data Scientists geleiteten Masterclasses hat bereits über 10.000 Alumni überzeugt und den Kursen eine Abschlussquote von über 94 % verliehen.

Unsere pädagogische Methode basiert auf dem Prinzip Learning-by-Doing:
  • Praktische Anwendung: Alle unsere Lernmodule beinhalten Online-Übungen, damit Du die im Kurs entwickelten Konzepte direkt anwenden kannst.
  • Masterclass: Für jedes Modul werden 1 bis 2 Masterclasses live mit einem Dozenten organisiert, die es ermöglichen, Deine Fragen und eventuelle Probleme zu klären sowie Methoden und Werkzeuge  aus dem Bereich der Data Science zu besprechen.

 

Die Ziele des Data Scientist

Data Scientists entwickeln komplexe Analysemodelle, um Informationen aus Datenbanken zu extrahieren. Diese können verwendet werden, um das Verhalten von der Kundschaft vorherzusagen oder um geschäftliche oder betriebliche Risiken zu identifizieren.

Untersuchen

Untersuche die Unternehmensdaten und lege die Daten fest, die extrahiert und verarbeitet werden sollen.

Analysieren

Rufe die relevanten Daten ab und analysiere diejenigen, die sich auf den Produktionsprozess des Unternehmens, den Verkauf oder einen Kundendatensatz beziehen.

Prognostizieren

Erstelle prädiktive Modelle, um Entwicklungen vorherzusagen oder neue Zielwerte für das Unternehmen zu bestimmen.

Modellieren

Werte die Ergebnisse der Datenanalyse und Modellierung aus, um sie für andere Abteilungen des Unternehmens lesbar, nutzbar und umsetzbar zu machen.

Am besten gleich hier einen Termin für eine individuelle Beratung vereinbaren!

Kosten für diese anerkannte Weiterbildung: 5.990 EUR

Wie kannst Du Deine Weiterbildung finanzieren?

Für die Finanzierung Deiner Weiterbildung zum Data Scientist kannst Du zwischen mehreren Optionen wählen. Wenn Du arbeitslos, arbeitssuchend oder von Arbeitslosigkeit bedroht bist, hast Du gute Chancen auf den Erhalt des Bildungsgutscheins. Dadurch werden die gesamten Weiterbildungskosten für Dich von der Agentur für Arbeit bzw. dem Jobcenter übernommen.

Als Arbeitnehmer kannst Du mit Deinem Arbeitgeber die Möglichkeit der teilweisen oder gänzlichen Finanzierung Deiner Weiterbildung besprechen.
Alternativ kannst Du die Kosten der Weiterbildung aber auch selbst tragen. Falls Du den gesamten Betrag nicht auf einmal stemmen kannst, besteht für Dich ebenfalls die Möglichkeit der Ratenzahlung. Dadurch kannst Du bereits ab 375 € pro Monat mit Deiner Data Weiterbildung beginnen.

Für weitere Informationen, Fragen oder direkt zur Anmeldung: datascientest.com/de/weiterbildung-data-scientist