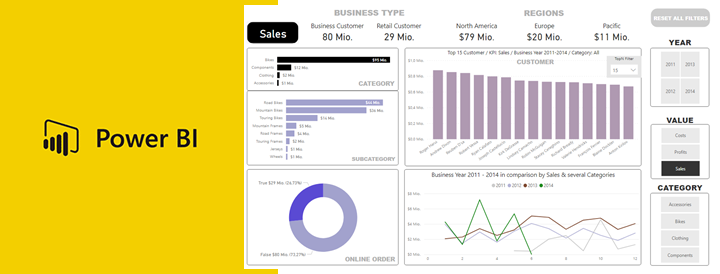
Dies ist ein Artikel der Artikel-Serie “BI Tools im Vergleich – Einführung und Motivation“. Solltet ihr gerade erst eingestiegen sein, dann schaut euch ruhig vorher einmal die einführenden Worte und die Ausführungen zur Datenbasis an. Power BI machte den Auftakt und ihr findet den Artikel hier.
Lizenzmodell
Tableau stellt seinen Kunden zu allererst vor die Wahl, wo und von wem die Infrastruktur betrieben werden soll. Einen preislichen Vorteil hat der Kunde bei der Wahl einer selbstverwaltenden Lösung unter Nutzung von Tableau Server. Die Alternative ist eine Cloud-Lösung, bereitgestellt und verwaltet von Tableau. Bei dieser Variante wird Tableau Server durch Tableau Online ersetzt, wobei jede dieser Optionen die gleichen Funktionalitäten mit sich bringen. Bereits das Lizenzmodell definiert unterschiedliche Rollen an Usern, welche in drei verschiedene Lizenztypen unterteilt und unterschiedlich bepreist sind (siehe Grafik). So kann der User die Rolle eines Creators, Explorers oder Viewers einnehmen.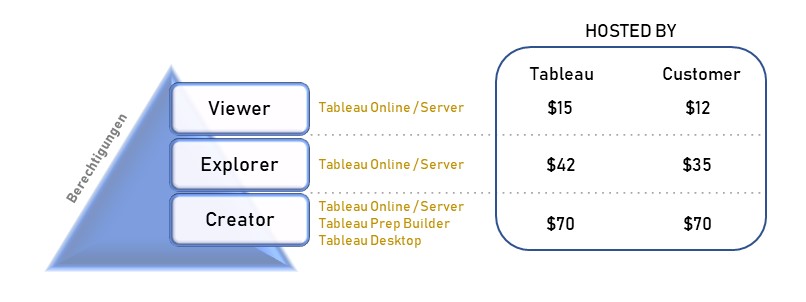 Der Creator ist befähigt, alle Funktionen von Tableau zu nutzen, sofern ein Unternehmen die angebotenen Add-ons hinzukauft. Die Lizenz Explorer ermöglicht es dem User, durch den Creator vordefinierte Datasets in Eigenregie zu analysieren und zu visualisieren. Demnach obliegt dem Creator, und somit einer kleinen Personengruppe, die Datenbereitstellung, womit eine Single Source of Truth garantiert werden soll. Der Viewer hat nur die Möglichkeit Berichte zu konsumieren, zu teilen und herunterzuladen. Wobei in Bezug auf Letzteres der Viewer limitiert ist, da dieser nicht die kompletten zugrundeliegenden Daten herunterladen kann. Lediglich eine Aggregation, auf welcher die Visualisierung beruht, kann heruntergeladen werden. Ein Vergleich zeigt die wesentlichen Berechtigungen je Lizenz.
Der Creator ist befähigt, alle Funktionen von Tableau zu nutzen, sofern ein Unternehmen die angebotenen Add-ons hinzukauft. Die Lizenz Explorer ermöglicht es dem User, durch den Creator vordefinierte Datasets in Eigenregie zu analysieren und zu visualisieren. Demnach obliegt dem Creator, und somit einer kleinen Personengruppe, die Datenbereitstellung, womit eine Single Source of Truth garantiert werden soll. Der Viewer hat nur die Möglichkeit Berichte zu konsumieren, zu teilen und herunterzuladen. Wobei in Bezug auf Letzteres der Viewer limitiert ist, da dieser nicht die kompletten zugrundeliegenden Daten herunterladen kann. Lediglich eine Aggregation, auf welcher die Visualisierung beruht, kann heruntergeladen werden. Ein Vergleich zeigt die wesentlichen Berechtigungen je Lizenz.
Der Einstieg bei Tableau ist für Organisationen nicht unter 106 Lizenzen (100 Viewer, 5 Explorer, 1 Creator) möglich, und Kosten von mindestens $1445 im Monat müssen einkalkuliert werden.
Wie bereits erwähnt, existieren Leistungserweiterungen, sogennante Add-ons. Die selbstverwaltende Alternative unter Nutzung von Tableau Server (hosted by customer) kann um das Tableau Data Management Add‑on und das Server Management Add‑on erweitert werden. Hauptsächlich zur Serveradministration, Datenverwaltung und -bereitstellung konzipiert sind die Features in vielen Fällen entbehrlich. Für die zweite Alternative (hosted by Tableau) kann der Kunde ebenfalls das Tableau Data Management Add‑on sowie sogenannte Resource Blocks dazu kaufen. Letzteres lässt bereits im Namen einen kapazitätsabhängigen Kostenfaktor vermuten, welcher zur Skalierung dient. Die beiden Add‑ons wiederum erhöhen die Kosten einer jeden Lizenz, was erhebliche Kostensteigerungen mit sich bringen kann. Das Data Management Add‑on soll als Beispiel die Kostenrelevanz verdeutlichen. Es gelten $5,50 je Lizenz für beide Hosting Varianten. Ein Unternehmen bezieht 600 Lizenzen (50 Creator, 150 Explorer und 400 Viewer) und hosted Tableau Server auf einer selbstgewählten Infrastruktur. Beim Zukauf des Add‑ons erhöht sich die einzelne Viewer-Lizenz bei einem Basispreis von $12 um 46%. Eine nicht unrelevante Größe bei der Vergabe neuer Viewer-Lizenzen, womit sich ein jedes Unternehmen mit Wachstumsambitionen auseinandersetzen sollte. Die Gesamtkosten würden nach geschilderter Verteilung der Lizenzen um 24% steigen (Anmerkung: eventuelle Rabatte sind nicht mit einbezogen). Die Tatsache, dass die Zuschläge für alle Lizenzen gelten, kann zumindest kritisch hinterfragt werden.
Ein weiterer, anfangs oft unterschätzter Kostenfaktor ist die Anzahl der Explorer-Lizenzen. Das Verhältnis der Explorer-Lizenzen an der Gesamtanzahl wächst in vielen Fällen mittelfristig nach der Einführungsphase stark an. Häufig wird Tableau als eine neue State of the Art Reporting Lösung mit schönen bunten Bildern betrachtet und dessen eigentliche Stärke, die Generierung von neuen Erkenntnissen mittels Data Discovery, wird unterschätzt. Hier kommt die Explorer Lizenz ins Spiel, welche ca. das Dreifache einer Viewer Lizenz kostet und den User befähigt, tiefer in die Daten einzusteigen.
Nichtdestotrotz kann man behaupten, dass das Lizenzmodell sehr transparent ist. Tableau selbst wirbt damit, dass keine versteckten Kosten auf den Kunden zukommen. Das Lizenzmodell ist aber nicht nur auf die Endkunden ausgerichtet, sondern bietet mit Tableau Server auch ein besonders auf Partner ausgerichtetes Konzept an. Serviceanbieter können so Lizenzen erwerben und in das eigene Angebot zu selbst gewählten Konditionen aufnehmen. Eine Server Instanz reicht aus, da das Produkt auch aus technischer Sicht mit sogenannten Sites auf verschiedene Stakeholder ausgerichtet werden kann.
Community & Features von anderen Entwicklern
Die Bedeutung einer breiten Community soll hier noch einmal hervorgehoben werden. Für Nutzer ist der Austausch über Probleme und Herausforderungen sowie technischer und organisatorischer Art äußerst wichtig, und auch der Softwarehersteller profitiert davon erheblich. Nicht nur, dass der Support teilweise an die eigenen Nutzer abgegeben wird, auch kann der Anbieter bestehende Features zielgerichteter optimieren und neue Features der Nachfrage anpassen. Somit steht die Tableau Community der Power BI Community in nichts nach. Zu den meisten Themen wird man schnell fündig in diversen Foren wie auch auf der Tableau Webseite. Es existiert die klassische Community Plattform, aber auch eine Tableau Besonderheit: Tableau Public. Es handelt sich hierbei um eine kostenlose Möglichkeit eine abgespeckte Version von Tableau zu nutzen und Inhalte auf der gleichnamigen Cloud zu veröffentlichen. Ergänzend sind etliche Lernvideos auf den einschlägigen Seiten fast zu jedem Thema zu finden und komplettieren das Support-Angebot.
Zusätzlich bietet Tableau sogenannte Admin-Tools aus eigenem Hause an, welche als Plug ins eingebunden werden können. Tableau unterscheidet dabei zwischen Community Supported Tools (z.B. TabMon) und Tableau Supported Tools (z.B. Tabcmd).
Ebenfalls bietet Tableau seit der Version 2018.2 dritten Entwicklern eine sogenannte Extensions API an und ermöglicht diesen damit, auf Basis der Tableau-Produkte eigene Produkte zu entwickeln. Erst kürzlich wurde mit Sandboxed Extensions in der Version 2019.4 ein wesentlicher Schritt hin zu einer höheren Datensicherheit gemacht, so dass es zukünftig zwei Gruppen von Erweiterungen geben wird. Die erste und neue Gruppe Sandboxed Extensions beinhaltet alle Erweiterungen, bei denen die Daten das eigene Netzwerk bzw. die Cloud nicht verlassen. Alle übrigen Erweiterungen werden in der zweiten Gruppe Network-Enabled Extensions zusammengefasst. Diese kommunizieren wie gehabt mit der Außenwelt, um den jeweiligen Service bereitzustellen.
Grundsätzlich ist Tableau noch zurückhaltend, wenn es um Erweiterungen des eigenen Produktportfolios geht. Deshalb ist die Liste mit insgesamt 37 Erweiterungen von 19 Anbietern noch recht überschaubar.
Daten laden & transformieren
Bevor der Aufbau der Visualisierungen beginnen kann, müssen die Daten fehlerfrei in Logik und in Homogenität in das Tool geladen werden. Zur Umsetzung dieser Anforderungen bietet sich ein ETL Tool an, und mit der Einführung von Tableau Prep Builder im April 2018 gibt der Softwareentwickler dem Anwender ein entsprechendes Tool an die Hand. Die Umsetzung ist sehr gut gelungen und die Bedienung ist sogar Analysten ohne Kenntnisse von Programmiersprachen möglich. Natürlich verfügen die zur Visualisierung gedachten Tools im Produktsortiment (Tableau Desktop, Server und Online) ebenfalls über (gleiche) Werkzeuge zur Datenmanipulierung. Jedoch verfügt Tableau Prep Builder dank seiner erweiterten Visualisierungen zur Transformation und Zusammenführung von Daten über hervorragende Werkzeuge zur Überprüfung und Analyse der Datengrundlage sowie der eigenen Arbeit.
Als Positivbeispiel ist die Visualisierung zu den JOIN-Operationen hervorzuheben, welche dem Anwender auf einen Blick zeigt, wie viele Datensätze vom JOIN betroffen sind und letztendlich auch, wie viele Datensätze in die Output-Tabelle eingeschlossen werden (siehe Grafik).
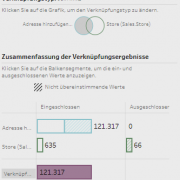
Zur Datenzusammenführung dienen klassische JOIN- und UNION-Befehle und die Logik entspricht den SQL-Befehlen. Das Ziel dabei ist die Generierung einer Extract-Datei und somit einer zweidimensionalen Tabelle für den Bau von Visualisierungen.
Exkurs – Joins in Power BI:
Erst bei der Visualisierung führt Power BI (im Hintergrund) die Daten durch Joins verschiedener Tabellen zusammen, sofern man vorher ein Datenmodell fehlerfrei definiert hat und die Daten nicht bereits mittels Power Query zusammengeführt hat.
Alternativ können auch diverse Datenquellen in das Visualisierungstool geladen und entsprechend des Power BI-Ansatzes Daten zusammengeführt werden. Dieses sogenannte Data Blending rückt seit der Einführung von Tableau Prep Builder immer mehr in den Hintergrund und Tableau führt die User auch hin zu einer weiteren Komponente: Tableau Prep Conductor. Es ist Bestandteil des bereits erwähnten, kostenpflichtigen Tableau Data Management Add-ons und ergänzt die eingeschränkte Möglichkeit, in Tableau Prep Builder automatisierte Aktualisierungen zu planen.
Kalkulationen können, wie auch bei Power BI, teilweise über ein Userinterface (UI) getätigt werden. Jedoch bietet das UI weniger Möglichkeiten, die wirklich komplizierten Berechnungen vorzunehmen, und der User wird schneller mit der von Tableau entwickelten Sprache konfrontiert. Drei Kategorien von Berechnungen werden unterschieden:
- Einfache Berechnungen
- Detailgenauigkeits-Ausdrücke (Level of Detail, LOD)
- Tabellenberechnungen
Es gibt zwei wesentliche Fragestellungen bei der Auswahl der Berechnungsmethode.
1. Was soll berechnet werden? => Detailgenauigkeit?
Diese Frage klingt auf den ersten Blick simpel, kann aber komplexe Ausmaße annehmen. Tableau gibt hierzu aber einen guten Leitfaden für den Start an die Hand.
2. Wann soll berechnet werden?
Die Wahl der Berechnungsmethode hängt auch davon ab, wann welche Berechnung von der Software durchgeführt wird. Die Reihenfolge der Operationen zeigt die folgende Grafik.

Man braucht einiges an Übung, bis man eine gewisse Selbstsicherheit erlangt hat. Deshalb ist ein strukturiertes Vorgehen für komplexe Vorhaben ratsam.
Daten laden & transformieren: AdventureWorks2017Dataset
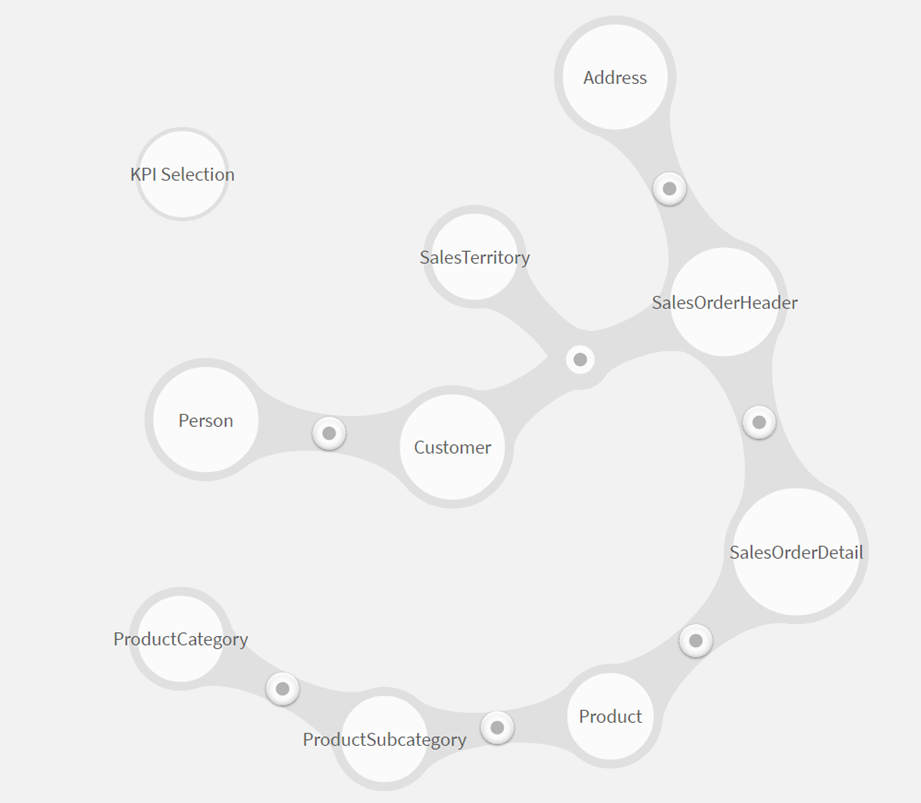
Wie bereits im ersten Artikel beschrieben, ist es nicht sehr sinnvoll, ein komplettes Datenmodell in ein BI-Tool zu laden, insbesondere wenn man nur wenige Informationen aus diesem benötigt. Ein für diese Zwecke angepasster View in der Datenbasis wäre aus vielerlei Hinsicht näher an einem Best Practice-Vorgehen. Nicht immer hat man die Möglichkeit, Best Practice im Unternehmen zu leben => siehe Artikel 1 der Serie.

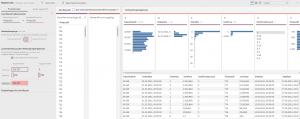
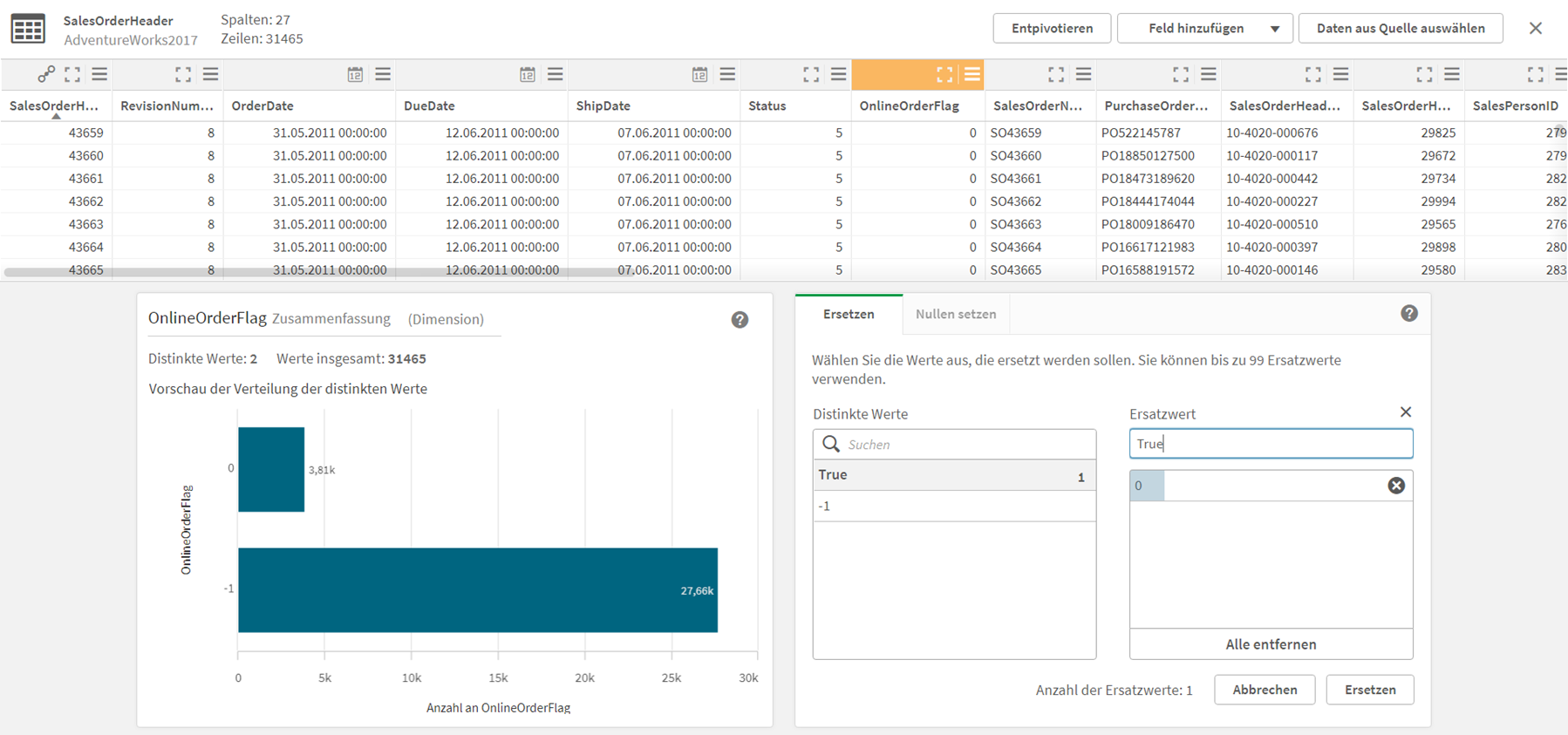
Erst durch die Nutzung von Tableau Prep wurde die komplexe Struktur der Daten deutlich. In Power BI fiel bei der Bereitstellung der Tabellen nicht auf, dass die Adressdaten zu den [Store Contact] nicht in der Tabelle [Adress] zu finden sind. Erst durch die Nutzung von Tableau Prep und einer Analyse zu den Joins, zeigte das Fehlen zuvor genannter Adressen für Stores auf. Weiterhin zeigte die Analyse des Joins von Handelswaren und dazugehöriger Lieferanten auch eine m:n Beziehung auf und somit eine Vervielfachung der Datensätze der output Tabelle.
Kurzum: Tableau Prep ist ein empfehlenswertes Tool, um die Datenbasis schnell zu durchdringen und aufwendige Datenbereitstellungen vorzunehmen.
Daten visualisieren
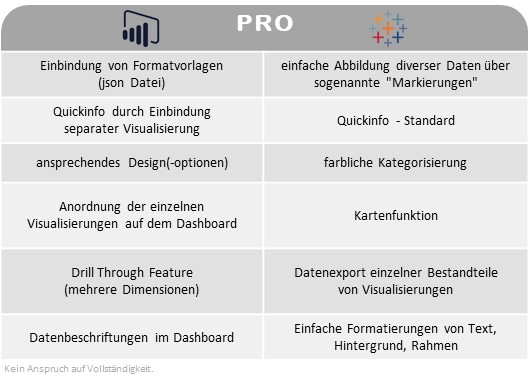
Erwartungsgemäß sind im Vergleich zwischen Tableau und Power BI einige Visualisierungen leichter und andere dagegen schwerer aufzubauen. Grundsätzlich bieten beide Tools einige vorprogrammierte Visualisierungsobjekte an, welche ohne großen Aufwand erstellt werden können. Interessant wird es beim Vergleich der Detailgenauigkeit der Visualisierungen, wobei es nebensächlich ist, ob es sich dabei um ein Balken- oder Liniendiagramm handelt.
Hands on! Dazu lädt Tableau ein, und das ist auch der beste Weg, um sich mit der Software vertraut zu machen. Für einen einfacheren Start sollte man sich mit zwei wesentlichen Konzepten vertraut machen:
Reihenfolge der Operationen
Yep! Wir hatten das Thema bereits. Ein Blick auf die Grafik beim Basteln einzelner Visualisierungen kann helfen! Jeder Creator und Explorer sollte sich vorher mit der Reihenfolge von Operationen vertraut machen. Das Konzept ist nicht selbsterklärend und Fehler fallen nicht sofort auf. Schaut einmal HIER rein! Tableau hat sich eine Stunde Zeit genommen, um das Konzept anhand von Beispielen zu erklären.
Starre Anordnung von Elementen
Visualisierungen werden erst in einem extra Arbeitsblatt entworfen und können mit anderen Arbeitsblättern in einem Dashboard verbaut werden. Die Anordnung der Elemente auf dem Dashboard kann frei erfolgen und/oder Elemente werden in einer Objekthierarchie abgelegt. Letzteres eignet sich gut für den Bau von Vorlagen und ist somit eine Stärke von Tableau. Das Vorgehen dabei ist nicht trivial, das heißt ein saloppes Reinschmeißen von Visualisierungen führt definitiv nicht zum Ziel.
Tim erklärt ziemlich gut, wie man vorgehen kann => HIER.
Tableau ist aus der Designperspektive limitiert, weshalb das Endergebnis, das Dashboard, nicht selten sehr eckig und kantig aussieht. Einfache visuelle Anpassungen wie abgerundete Kanten von Arbeitsblättern/Containern sind nicht möglich. Designtechnisch hat Tableau daher noch Luft nach oben!
Fazit
Der Einstieg für kleine Unternehmen mit Tableau ist nur unter sehr hohem Kostenaufwand möglich, aufgrund von preisintensiven Lizenzen und einer Mindestabnahme an Lizenzen. Aber auch bei einem hohen Bedarf an Lizenzen befindet sich Tableau im höheren Preissegment. Jedoch beinhalten Tableaus Lizenzgebühren bereits Kosten, welche bei der Konkurrenz erst durch die Nutzung ersichtlich werden, da bei ihnen die Höhe der Kosten stärker von der beanspruchten Kapazität abhängig ist. Tableau bietet seinen Kunden damit eine hohe Transparenz über ein zwar preisintensives, aber sehr ausgereiftes Produktportfolio.
Tableau legt mit einer lokalen Option, welche die gleichen Funktionalitäten beinhaltet wie die cloudbasierte Alternative, ein Augenmerk auf Kunden mit strengen Data Governance-Richtlinien. Sandboxed Extensions sind ein weiteres Beispiel für das Bewusstsein für eine hohe Datensicherheit. Jedoch ist das Angebot an Extensions, also das Angebot dritter Entwickler, ausbaufähig. Eine breit aufgestellte Community bietet nicht nur dritten Entwicklern eine gute Geschäftsgrundlage, sondern auch Nutzern zu fast jedem Thema eine Hilfestellung.
Tableau Prep Builder => TOP!
Mit diesem Tool kann die Datengrundlage super einfach analysiert werden und Datenmanipulationen sind einfach durchzuführen. Die Syntax und die Verwendung von Berechnungen bedarf einiger Übung, aber wenn man die wesentlichen Konzepte verstanden hat, dann sind Berechnungen schnell erstellt.
Ein Dashboard kann zu 90 % in fast jedem Tool gleich aussehen. Der Weg dorthin ist oft ein anderer und je nach Anforderung bei einem Tool leichter als bei einem anderen. Tableau bietet ein komplexes Konzept, sodass auch die außergewöhnlichsten Anforderungen erfüllt werden können. Jedoch ist das zugrundliegende Design oft sehr kantig und nicht immer zeitgemäß.
Fortsetzung folgt… MicroStrategy







 Der Creator ist befähigt, alle Funktionen von Tableau zu nutzen, sofern ein Unternehmen die angebotenen Add-ons hinzukauft. Die Lizenz Explorer ermöglicht es dem User, durch den Creator vordefinierte Datasets in Eigenregie zu analysieren und zu visualisieren. Demnach obliegt dem Creator, und somit einer kleinen Personengruppe, die Datenbereitstellung, womit eine Single Source of Truth garantiert werden soll. Der Viewer hat nur die Möglichkeit Berichte zu konsumieren, zu teilen und herunterzuladen. Wobei in Bezug auf Letzteres der Viewer limitiert ist, da dieser nicht die kompletten zugrundeliegenden Daten herunterladen kann. Lediglich eine Aggregation, auf welcher die Visualisierung beruht, kann heruntergeladen werden. Ein
Der Creator ist befähigt, alle Funktionen von Tableau zu nutzen, sofern ein Unternehmen die angebotenen Add-ons hinzukauft. Die Lizenz Explorer ermöglicht es dem User, durch den Creator vordefinierte Datasets in Eigenregie zu analysieren und zu visualisieren. Demnach obliegt dem Creator, und somit einer kleinen Personengruppe, die Datenbereitstellung, womit eine Single Source of Truth garantiert werden soll. Der Viewer hat nur die Möglichkeit Berichte zu konsumieren, zu teilen und herunterzuladen. Wobei in Bezug auf Letzteres der Viewer limitiert ist, da dieser nicht die kompletten zugrundeliegenden Daten herunterladen kann. Lediglich eine Aggregation, auf welcher die Visualisierung beruht, kann heruntergeladen werden. Ein