Tag Archive for: AI
KI in der Abschlussprüfung – Podcast mit Benjamin Aunkofer
/in Artificial Intelligence, Big Data, Data Science, Insights, Interviews, Machine Learning, Reinforcement Learning/by AUDAVISGemeinsam mit Prof. Kai-Uwe Marten von der Universität Ulm und dortiger Direktor des Instituts für Rechnungswesen und Wirtschaftsprüfung, bespricht Benjamin Aunkofer, Co-Founder und Chief AI Officer von AUDAVIS, die Potenziale und heutigen Möglichkeiten von der Künstlichen Intelligenz (KI) in der Jahresabschlussprüfung bzw. allgemein in der Wirtschaftsprüfung: KI als Co-Pilot für den Abschlussprüfer.
Inhaltlich behandelt werden u.a. die Möglichkeiten von überwachtem und unüberwachten maschinellem Lernen, die Möglichkeit von verteiltem KI-Training auf Datensätzen sowie warum Large Language Model (LLM) nur für einige bestimmte Anwendungsfälle eine adäquate Lösung darstellen.
Die neue Folge ist frei verfügbar zum visuellen Ansehen oder auch nur zum Anhören, bitte besuchen Sie dafür einen der folgenden Links:
… Spotify: Podcast “Wirtschaftsprüfung kann mehr” auf Spotify
… YouTube: Ulmer Forum für Wirtschaftswissenschaften auf Youtube
… und auf der Podcast-Webseite unter Podcast – Wirtschaftsprüfung kann mehr!
KI-gestützte Datenanalysen als Kompass für Unternehmen: Chancen und Herausforderungen
/in Artificial Intelligence, Big Data, Business Analytics, Data Engineering, Data Science, Main Category, Use Case/by RedaktionIT-Verantwortliche, Datenadministratoren, Analysten und Führungskräfte, sie alle stehen vor der Aufgabe, eine Flut an Daten effizient zu nutzen, um die Wettbewerbsfähigkeit ihres Unternehmens zu steigern. Die Fähigkeit, diese gewaltigen Datenmengen effektiv zu analysieren, ist der Schlüssel, um souverän durch die digitale Zukunft zu navigieren. Gleichzeitig wachsen die Datenmengen exponentiell, während IT-Budgets zunehmend schrumpfen, was Verantwortliche unter enormen Druck setzt, mit weniger Mitteln schnell relevante Insights zu liefern. Doch veraltete Legacy-Systeme verlängern Abfragezeiten und erschweren Echtzeitanalysen großer und komplexer Datenmengen, wie sie etwa für Machine Learning (ML) erforderlich sind. An dieser Stelle kommt die Integration von Künstlicher Intelligenz (KI) ins Spiel. Sie unterstützt Unternehmen dabei, Datenanalysen schneller, kostengünstiger und flexibler zu gestalten und erweist sich über verschiedenste Branchen hinweg als unentbehrlich.
Was genau macht KI-gestützte Datenanalyse so wertvoll?
KI-gestützte Datenanalyse verändern die Art und Weise, wie Unternehmen Daten nutzen. Präzise Vorhersagemodelle antizipieren Trends und Kundenverhalten, minimieren Risiken und ermöglichen proaktive Planung. Beispiele sind Nachfrageprognosen, Betrugserkennung oder Predictive Maintenance. Diese Echtzeitanalysen großer Datenmengen führen zu fundierteren, datenbasierten Entscheidungen.
Ein aktueller Report zur Nutzung von KI-gestützter Datenanalyse zeigt, dass Unternehmen, die KI erfolgreich implementieren, erhebliche Vorteile erzielen: schnellere Entscheidungsfindung (um 25%), reduzierte Betriebskosten (bis zu 20%) und verbesserte Kundenzufriedenheit (um 15%). Die Kombination von KI, Data Analytics und Business Intelligence (BI) ermöglicht es Unternehmen, das volle Potenzial ihrer Daten auszuschöpfen. Tools wie AutoML integrieren sich in Analytics-Datenbanken und ermöglichen BI-Teams, ML-Modelle eigenständig zu entwickeln und zu testen, was zu Produktivitätssteigerungen führt.
Herausforderungen und Chancen der KI-Implementierung
Die Implementierung von KI in Unternehmen bringt zahlreiche Herausforderungen mit sich, die IT-Profis und Datenadministratoren bewältigen müssen, um das volle Potenzial dieser Technologien zu nutzen.
- Technologische Infrastruktur und Datenqualität: Veraltete Systeme und unzureichende Datenqualität können die Effizienz der KI-Analyse erheblich beeinträchtigen. So sind bestehende Systeme häufig überfordert mit der Analyse großer Mengen aktueller und historischer Daten, die für verlässliche Predictive Analytics erforderlich sind. Unternehmen müssen zudem sicherstellen, dass ihre Daten vollständig, aktuell und präzise sind, um verlässliche Ergebnisse zu erzielen.
- Klare Ziele und Implementierungsstrategien: Ohne klare Ziele und eine durchdachte Strategie, die auch auf die Geschäftsstrategie einzahlt, können KI-Projekte ineffizient und ergebnislos verlaufen. Eine strukturierte Herangehensweise ist entscheidend für den Erfolg.
- Fachkenntnisse und Schulung: Die Implementierung von KI erfordert spezialisiertes Wissen, das in vielen Unternehmen fehlt. Die Kosten für Experten oder entsprechende Schulungen können eine erhebliche finanzielle Hürde darstellen, sind aber Grundlage dafür, dass die Technologie auch effizient genutzt wird.
- Sicherheit und Compliance: Auch Governance-Bedenken bezüglich Sicherheit und Compliance können ein Hindernis darstellen. Eine strategische Herangehensweise, die sowohl technologische, ethische als auch organisatorische Aspekte berücksichtigt, ist also entscheidend. Unternehmen müssen sicherstellen, dass ihre KI-Lösungen den rechtlichen Anforderungen entsprechen, um Datenschutzverletzungen zu vermeiden. Flexible Bereitstellungsoptionen in der Public Cloud, Private Cloud, On-Premises oder hybriden Umgebungen sind entscheidend, um Plattform- und Infrastrukturbeschränkungen zu überwinden.
Espresso AI von Exasol: Ein Lösungsansatz
Exasol hat mit Espresso AI eine Lösung entwickelt, die Unternehmen bei der Implementierung von KI-gestützter Datenanalyse unterstützt und KI mit Business Intelligence (BI) kombiniert. Espresso AI ist leistungsstark und benutzerfreundlich, sodass auch Teammitglieder ohne tiefgehende Data-Science-Kenntnisse mit neuen Technologien experimentieren und leistungsfähige Modelle entwickeln können. Große und komplexe Datenmengen können in Echtzeit verarbeitet werden – besonders für datenintensive Branchen wie den Einzelhandel oder E-Commerce ist die Lösung daher besonders geeignet. Und auch in Bereichen, in denen sensible Daten im eigenen Haus verbleiben sollen oder müssen, wie dem Finanz- oder Gesundheitsbereich, bietet Espresso die entsprechende Flexibilität – die Anwender haben Zugriff auf Realtime-Datenanalysen, egal ob sich ihre Daten on-Premise, in der Cloud oder in einer hybriden Umgebung befinden. Dank umfangreicher Integrationsmöglichkeiten mit bestehenden IT-Systemen und Datenquellen wird eine schnelle und reibungslose Implementierung gewährleistet.
Chancen durch KI-gestützte Datenanalysen
Der Einsatz von KI-gestützten Datenintegrationswerkzeugen automatisiert viele der manuellen Prozesse, die traditionell mit der Vorbereitung und Bereinigung von Daten verbunden sind. Dies entlastet Teams nicht nur von zeitaufwändiger Datenaufbereitung und komplexen Datenintegrations-Workflows, sondern reduziert auch das Risiko menschlicher Fehler und stellt sicher, dass die Daten für die Analyse konsistent und von hoher Qualität sind. Solche Werkzeuge können Daten aus verschiedenen Quellen effizient zusammenführen, transformieren und laden, was es den Teams ermöglicht, sich stärker auf die Analyse und Nutzung der Daten zu konzentrieren.
Die Integration von AutoML-Tools in die Analytics-Datenbank eröffnet Business-Intelligence-Teams neue Möglichkeiten. AutoML (Automated Machine Learning) automatisiert viele der Schritte, die normalerweise mit dem Erstellen von ML-Modellen verbunden sind, einschließlich Modellwahl, Hyperparameter-Tuning und Modellvalidierung.
Über Exasol-CEO Martin Golombek
Mathias Golombek ist seit Januar 2014 Mitglied des Vorstands der Exasol AG. In seiner Rolle als Chief Technology Officer verantwortet er alle technischen Bereiche des Unternehmens, von Entwicklung, Produkt Management über Betrieb und Support bis hin zum fachlichen Consulting.
Über Mathias Golombek

Nach seinem Informatikstudium, in dem er sich vor allem mit Datenbanken, verteilten Systemen, Softwareentwicklungsprozesse und genetischen Algorithmen beschäftigte, stieg Mathias Golombek 2004 als Software Developer bei der Nürnberger Exasol AG ein. Seitdem ging es für ihn auf der Karriereleiter steil nach oben: Ein Jahr danach verantwortete er das Database-Optimizer-Team. Im Jahr 2007 folgte die Position des Head of Research & Development. 2014 wurde Mathias Golombek schließlich zum Chief Technology Officer (CTO) und Technologie-Vorstand von Exasol benannt. In seiner Rolle als Chief Technology Officer verantwortet er alle technischen Bereiche des Unternehmens, von Entwicklung, Product Management über Betrieb und Support bis hin zum fachlichen Consulting.
Er ist der festen Überzeugung, dass sich jedes Unternehmen durch seine Grundwerte auszeichnet und diese stets gelebt werden sollten. Seit seiner Benennung zum CTO gibt Mathias Golombek in Form von Fachartikeln, Gastbeiträgen, Diskussionsrunden und Interviews Einblick in die Materie und fördert den Wissensaustausch.
Data Jobs – Podcast-Folge mit Benjamin Aunkofer
/in Artificial Intelligence, Big Data, Business Analytics, Business Intelligence, Data Engineering, Data Science, Insights, Interviews, Main Category, Process Mining/by RedaktionIn der heutigen Geschäftswelt ist der Einsatz von Daten unerlässlich, insbesondere für Unternehmen mit über 100 Mitarbeitern, die erfolgreich bleiben möchten. In der Podcast-Episode “Data Jobs – Was brauchst Du, um im Datenbereich richtig Karriere zu machen?” diskutieren Dr. Christian Krug und Benjamin Aunkofer, Gründer von DATANOMIQ, wie Angestellte ihre Datenkenntnisse verbessern und damit ihre berufliche Laufbahn aktiv vorantreiben können. Dies steigert nicht nur ihren persönlichen Erfolg, sondern erhöht auch den Nutzen und die Wettbewerbsfähigkeit des Unternehmens. Datenkompetenz ist demnach ein wesentlicher Faktor für den Erfolg sowohl auf individueller als auch auf Unternehmensebene.
In dem Interview erläutert Benjamin Aunkofer, wie man den Einstieg auch als Quereinsteiger schafft. Das Sprichwort „Ohne Fleiß kein Preis“ trifft besonders auf die Entwicklung beruflicher Fähigkeiten zu, insbesondere im Bereich der Datenverarbeitung und -analyse. Anstelle den Abend mit Serien auf Netflix zu verbringen, könnte man die Zeit nutzen, um sich durch Fachliteratur weiterzubilden. Es gibt eine Vielzahl von Büchern zu Themen wie Data Science, Künstliche Intelligenz, Process Mining oder Datenstrategie, die wertvolle Einblicke und Kenntnisse bieten können.
Der Nutzen steht in einem guten Verhältnis zum Aufwand, so Benjamin Aunkofer. Für diejenigen, die wirklich daran interessiert sind, in eine Datenkarriere einzusteigen, stehen die Türen offen. Der Einstieg erfordert zwar Engagement und Lernbereitschaft, ist aber für entschlossene Individuen absolut machbar. Dabei muss man nicht unbedingt eine Laufbahn als Data Scientist anstreben. Jede Fachkraft und insbesondere Führungskräfte können erheblich davon profitieren, die Grundlagen von Data Engineering und Data Science zu verstehen. Diese Kenntnisse ermöglichen es, fundiertere Entscheidungen zu treffen und die Potenziale der Datenanalyse optimal für das Unternehmen zu nutzen.

Podcast-Folge mit Benjamin Aunkofer und Dr. Christian Krug darüber, wie Menschen mit Daten Karriere machen und den Unternehmenserfolg herstellen.
Zur Podcast-Folge auf Spotify: https://open.spotify.com/show/6Ow7ySMbgnir27etMYkpxT?si=dc0fd2b3c6454bfa
Zur Podcast-Folge auf iTunes: https://podcasts.apple.com/de/podcast/unf-ck-your-data/id1673832019
Zur Podcast-Folge auf Google: https://podcasts.google.com/feed/aHR0cHM6Ly9mZWVkcy5jYXB0aXZhdGUuZm0vdW5mY2steW91ci1kYXRhLw?ep=14
Zur Podcast-Folge auf Deezer: https://deezer.page.link/FnT5kRSjf2k54iib6
Espresso AI: Q&A mit Mathias Golombek, CTO bei Exasol
/in Artificial Intelligence, Big Data, Business Analytics, Business Intelligence, Data Engineering, Data Science, Main Category/by RedaktionNahezu alle Unternehmen beschäftigen sich heute mit dem Thema KI und die überwiegende Mehrheit hält es für die wichtigste Zukunftstechnologie – dennoch tun sich nach wie vor viele schwer, die ersten Schritte in Richtung Einsatz von KI zu gehen. Woran scheitern Initiativen aus Ihrer Sicht?
Zu den größten Hindernissen zählen Governance-Bedenken, etwa hinsichtlich Themen wie Sicherheit und Compliance, unklare Ziele und eine fehlende Implementierungsstrategie. Mit seinen flexiblen Bereitstellungsoptionen in der Public/Private Cloud, on-Premises oder in hybriden Umgebungen macht Exasol seine Kunden unabhängig von bestimmten Plattform- und Infrastrukturbeschränkungen, sorgt für die unkomplizierte Integration von KI-Funktionalitäten und ermöglicht Zugriff auf Datenerkenntnissen in real-time – und das, ohne den gesamten Tech-Stack austauschen zu müssen.
Dies ist der eine Teil – der technologische Teil – die Schritte, die die Unternehmen –selbst im Vorfeld gehen müssen, sind die Festlegung von klaren Zielen und KPIs und die Etablierung einer Datenkultur. Das Management sollte für Akzeptanz sorgen, indem es die Vorteile der Nutzung klar beleuchtet, Vorbehalte ernst nimmt und sie ausräumt. Der Weg zum datengetriebenen Unternehmen stellt für viele, vor allem wenn sie eher traditionell aufgestellt sind, einen echten Paradigmenwechsel dar. Führungskräfte sollten hier Orientierung bieten und klar darlegen, welche Rolle die Nutzung von Daten und der Einsatz neuer Technologien für die Zukunftsfähigkeit von Unternehmen und für jeden Einzelnen spielen. Durch eine Kultur der offenen Kommunikation werden Teams dazu ermutigt, digitale Lösungen zu finden, die sowohl ihren individuellen Anforderungen als auch den Zielen des Unternehmens entsprechen. Dazu gehört es natürlich auch, die eigenen Teams zu schulen und mit dem entsprechenden Know-how auszustatten.
Wie unterstützt Exasol die Kunden bei der Implementierung von KI?
Datenabfragen in natürlicher Sprache können, das ist spätestens seit dem Siegeszug von ChatGPT klar, generativer KI den Weg in die Unternehmen ebnen und ihnen ermöglichen, sich datengetrieben aufzustellen. Mit der Integration von Veezoo sind auch die Kunden von Exasol Espresso in der Lage, Datenabfragen in natürlicher Sprache zu stellen und KI unkompliziert in ihrem Arbeitsalltag einzusetzen. Mit dem integrierten autoML-Tool von TurinTech können Anwender zudem durch den Einsatz von ML-Modellen die Performance ihrer Abfragen direkt in ihrer Datenbank maximieren. So gelingt BI-Teams echte Datendemokratisierung und sie können mit ML-Modellen experimentieren, ohne dabei auf Support von ihren Data-Science-Teams angewiesen zu sei.
All dies trägt zur Datendemokratisierung – ein entscheidender Punkt auf dem Weg zum datengetriebenen Unternehmen, denn in der Vergangenheit scheiterte die Umsetzung einer unternehmensweiten Datenstrategie häufig an Engpässen, die durch Data Analytics oder Data Science Teams hervorgerufen werden. Espresso AI ermöglicht Unternehmen einen schnelleren und einfacheren Zugang zu Echtzeitanalysen.
Was war der Grund, Exasol Espresso mit KI-Funktionen anzureichern?
Immer mehr Unternehmen suchen nach Möglichkeiten, sowohl traditionelle als auch generative KI-Modelle und -Anwendungen zu entwickeln – das entsprechende Feedback unserer Kunden war einer der Hauptfaktoren für die Entwicklung von Espresso AI.
Ziel der Unternehmen ist es, ihre Datensilos aufzubrechen – oft haben Data Science Teams viele Jahre lang in Silos gearbeitet. Mit dem Siegeszug von GenAI durch ChatGPT hat ein deutlicher Wandel stattgefunden – KI ist greifbarer geworden, die Technologie ist zugänglicher und auch leistungsfähiger geworden und die Unternehmen suchen nach Wegen, die Technologie gewinnbringend einzusetzen.
Um sich wirklich datengetrieben aufzustellen und das volle Potenzial der eigenen Daten und der Technologien vollumfänglich auszuschöpfen, müssen KI und Data Analytics sowie Business Intelligence in Kombination gebracht werden. Espresso AI wurde dafür entwickelt, um genau das zu tun.
Und wie sieht die weitere Entwicklung aus? Welche Pläne hat Exasol?
Eines der Schlüsselelemente von Espresso AI ist das AI Lab, das es Data Scientists ermöglicht, die In-Memory-Analytics-Datenbank von Exasol nahtlos und schnell in ihr bevorzugtes Data-Science-Ökosystem zu integrieren. Es unterstützt jede beliebige Data-Science-Sprache und bietet eine umfangreiche Liste von Technologie-Integrationen, darunter PyTorch, Hugging Face, scikit-learn, TensorFlow, Ibis, Amazon Sagemaker, Azure ML oder Jupyter.
Weitere Integrationen sind ein wichtiger Teil unserer Roadmap. Während sich die ersten auf die Plattformen etablierter Anbieter konzentrierten, werden wir unser AI Lab weiter ausbauen und es werden Integrationen mit Open-Source-Tools erfolgen. Nutzer werden so in der Lage sein, eine Umgebung zu schaffen, in der sich Data Scientists wohlfühlen. Durch die Ausführung von ML-Modellen direkt in der Exasol-Datenbank können sie so die maximale Menge an Daten nutzen und das volle Potenzial ihrer Datenschätze ausschöpfen.
 Über Exasol-CEO Martin Golombek
Über Exasol-CEO Martin Golombek
Mathias Golombek ist seit Januar 2014 Mitglied des Vorstands der Exasol AG. In seiner Rolle als Chief Technology Officer verantwortet er alle technischen Bereiche des Unternehmens, von Entwicklung, Produkt Management über Betrieb und Support bis hin zum fachlichen Consulting.
Über Exasol und Espresso AI
Sie leiden unter langsamer Business Intelligence, mangelnder Datenbank-Skalierung und weiteren Limitierungen in der Datenanalyse? Exasol bietet drei Produkte an, um Ihnen zu helfen, das Maximum aus Analytics zu holen und schnellere, tiefere und kostengünstigere Insights zu erzielen.
Kein Warten mehr auf das “Spinning Wheel”. Von Grund auf für Geschwindigkeit konzipiert, basiert Espresso auf einer einmaligen Datenbankarchitektur aus In-Memory-Caching, spaltenorientierter Datenspeicherung, “Massively Parallel Processing” (MPP), sowie Auto-Tuning. Damit können selbst die komplexesten Analysen beschleunigt und bessere Erkenntnisse in atemberaubender Geschwindigkeit geliefert werden.
Video Interview – Interim Management für Daten & KI
/in Interviews/by RedaktionData & AI im Unternehmen zu etablieren ist ein Prozess, der eine fachlich kompetente Führung benötigt. Hier kann Interim Management die Lösung sein.
Unternehmer stehen dabei vor großen Herausforderungen und stellen sich oft diese oder ähnliche Fragen:
- Welche Top-Level Strategie brauche ich?
- Wo und wie finde ich die ersten Show Cases im Unternehmen?
- Habe ich aktuell den richtigen Daten back-bone?
Diese Fragen beantwortet Benjamin Aunkofer (Gründer von DATANOMIQ und AUDAVIS) im Interview mit Atreus Interim Management. Er erläutert, wie Unternehmen die Disziplinen Data Science, Business Intelligence, Process Mining und KI zusammenführen können, und warum Interim Management dazu eine gute Idee sein kann.
Video Interview “Meet the Manager” auf Youtube mit Franz Kubbillum von Atreus Interim Management und Benjamin Aunkofer von DATANOMIQ.
Über Benjamin Aunkofer

Benjamin Aunkofer – Interim Manager für Data & AI, Gründer von DATANOMIQ und AUDAVIS.
Benjamin Aunkofer ist Gründer des Beratungs- und Implementierungspartners für Daten- und KI-Lösungen namens DATANOMIQ sowie Co-Gründer der AUDAVIS, einem AI as a Service für die Wirtschaftsprüfung.
Nach seiner Ausbildung zum Software-Entwickler (FI-AE IHK) und seinem Einstieg als Consultant bei Deloitte, gründete er 2015 die DATANOMIQ GmbH in Berlin und unterstütze mit mehreren kleinen Teams Unternehmen aus unterschiedlichen Branchen wie Handel, eCommerce, Finanzdienstleistungen und der produzierenden Industrie (Pharma, Automobilzulieferer, Maschinenbau). Er partnert mit anderen Unternehmensberatungen und unterstütze als externer Dienstleister auch Wirtschaftsprüfungsgesellschaften.
Der Projekteinstieg in Unternehmen erfolgte entweder rein projekt-basiert (Projektangebot) oder über ein Interim Management z. B. als Head of Data & AI, Chief Data Scientist oder Head of Process Mining.
Im Jahr 2023 gründete Benjamin Aunkofer mit zwei Mitgründern die AUDAVIS GmbH, die eine Software as a Service Cloud-Plattform bietet für Wirtschaftsprüfungsgesellschaften, Interne Revisionen von Konzernen oder für staatliche Prüfung von Finanztransaktionen.
Podcast – KI in der Wirtschaftsprüfung
/in Artificial Intelligence, Audit Analytics, Interviews/by RedaktionDie Verwendung von Künstlicher Intelligenz (KI) in der Wirtschaftsprüfung, wie Sie es beschreiben, klingt in der Tat revolutionär. Die Integration von KI in diesem Bereich könnte enorme Vorteile mit sich bringen, insbesondere in Bezug auf Effizienzsteigerung und Genauigkeit.
 Die verschiedenen von Ihnen genannten Lernmethoden wie (Un-)Supervised Learning, Reinforcement Learning und Federated Learning bieten unterschiedliche Ansätze, um KI-Systeme für spezifische Anforderungen der Wirtschaftsprüfung zu trainieren. Diese Methoden ermöglichen es, aus großen Datenmengen Muster zu erkennen, Vorhersagen zu treffen und Entscheidungen zu optimieren.
Die verschiedenen von Ihnen genannten Lernmethoden wie (Un-)Supervised Learning, Reinforcement Learning und Federated Learning bieten unterschiedliche Ansätze, um KI-Systeme für spezifische Anforderungen der Wirtschaftsprüfung zu trainieren. Diese Methoden ermöglichen es, aus großen Datenmengen Muster zu erkennen, Vorhersagen zu treffen und Entscheidungen zu optimieren.
Der Artificial Auditor von AUDAVIS, der auf einer Kombination von verschiedenen KI-Verfahren basiert, könnte beispielsweise in der Lage sein, 100% der Buchungsdaten zu analysieren, was mit herkömmlichen Methoden praktisch unmöglich wäre. Dies würde nicht nur die Genauigkeit der Prüfung verbessern, sondern auch Betrug und Fehler effektiver aufdecken.
Der Punkt, den Sie über den Podcast Unf*ck Your Datavon Dr. Christian Krug und die Aussagen von Benjamin Aunkofer ansprechen, ist ebenfalls interessant. Es scheint, dass die Diskussion darüber, wie Datenautomatisierung und KI die Wirtschaftsprüfung effizienter gestalten können, bereits im Gange ist und dabei hilft, das Bewusstsein für diese Technologien zu schärfen und ihre Akzeptanz in der Branche zu fördern.
Es wird dabei im Podcast betont, dass die Rolle des menschlichen Prüfers durch KI nicht ersetzt, sondern ergänzt wird. KI kann nämlich dabei helfen, Routineaufgaben zu automatisieren und komplexe Datenanalysen durchzuführen, während menschliche Experten weiterhin für ihre Fachkenntnisse, ihr Urteilsvermögen und ihre Fähigkeit, den Kontext zu verstehen, unverzichtbar bleiben.
Insgesamt spricht Benjamin Aunkofer darüber, dass die Integration von KI in die Wirtschaftsprüfung bzw. konkret in der Jahresabschlussprüfung ein aufregender Schritt in Richtung einer effizienteren und effektiveren Zukunft sei, der sowohl Unternehmen als auch die gesamte Volkswirtschaft positiv beeinflussen wird.
Object-centric Process Mining on Data Mesh Architectures
/in Artificial Intelligence, Big Data, Business Analytics, Business Intelligence, Cloud, Data Engineering, Data Mining, Data Science, Data Warehousing, Industrie 4.0, Machine Learning, Main Category, Predictive Analytics, Process Mining/by Benjamin AunkoferIn addition to Business Intelligence (BI), Process Mining is no longer a new phenomenon, but almost all larger companies are conducting this data-driven process analysis in their organization.
The database for Process Mining is also establishing itself as an important hub for Data Science and AI applications, as process traces are very granular and informative about what is really going on in the business processes.
The trend towards powerful in-house cloud platforms for data and analysis ensures that large volumes of data can increasingly be stored and used flexibly. This aspect can be applied well to Process Mining, hand in hand with BI and AI.
New big data architectures and, above all, data sharing concepts such as Data Mesh are ideal for creating a common database for many data products and applications.
The Event Log Data Model for Process Mining
Process Mining as an analytical system can very well be imagined as an iceberg. The tip of the iceberg, which is visible above the surface of the water, is the actual visual process analysis. In essence, a graph analysis that displays the process flow as a flow chart. This is where the processes are filtered and analyzed.
The lower part of the iceberg is barely visible to the normal analyst on the tool interface, but is essential for implementation and success: this is the Event Log as the data basis for graph and data analysis in Process Mining. The creation of this data model requires the data connection to the source system (e.g. SAP ERP), the extraction of the data and, above all, the data modeling for the event log.
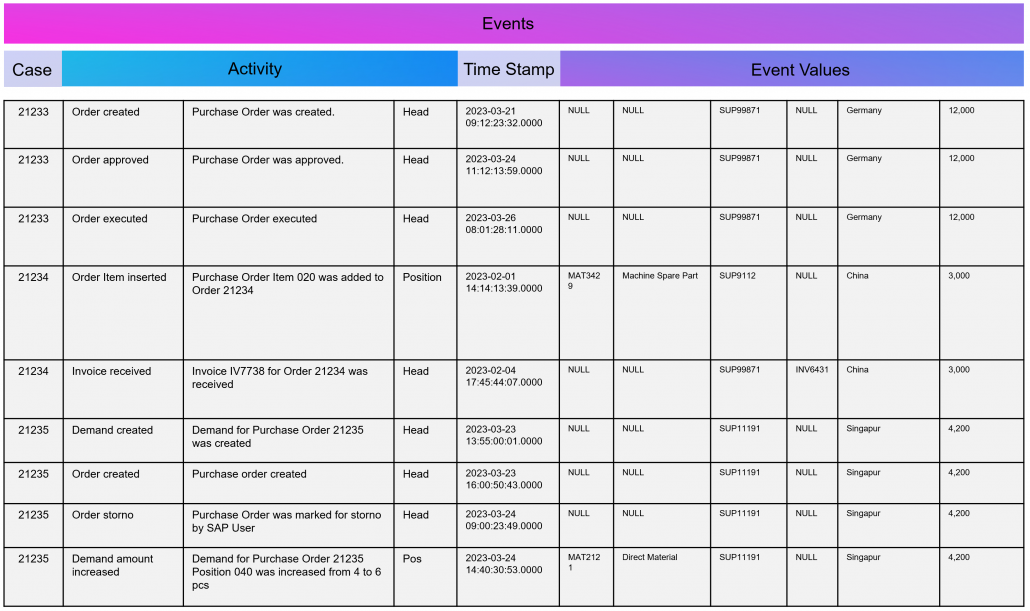
Simple Data Model for a Process Mining Event Log.
As part of data engineering, the data traces that indicate process activities are brought into a log-like schema. A simple event log is therefore a simple table with the minimum requirement of a process number (case ID), a time stamp and an activity description.
An Event Log can be seen as one big data table containing all the process information. Splitting this big table into several data tables is due to the goal of increasing the efficiency of storing the data in a normalized database.
The following example SQL-query is inserting Event-Activities from a SAP ERP System into an existing event log database table (one big table). It shows that events are based on timestamps (CPUDT, CPUTM) and refer each to one of a list of possible activities (dependent on VGABE).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
/* Inserting Events of Material Movement of Purchasing Processes */ INSERT INTO Event_Log SELECT EKBE.EBELN AS Einkaufsbeleg ,EKBE.EBELN + EKBE.EBELP AS PurchaseOrderPosition-- <-- Case ID of this Purchasing Process ,MSEG_MKPF.AUFNR AS CustomerOrder ,NULL AS CustomerOrderPosition ,CASE -- <-- Activitiy Description dependent on a flag WHEN MSEG_MKPF.VGABE = 'WA' THEN 'Warehouse Outbound for Customer Order' WHEN MSEG_MKPF.VGABE = 'WF' THEN 'Warehouse Inbound for Customer Order' WHEN MSEG_MKPF.VGABE = 'WO' THEN 'Material Movement for Manufacturing' WHEN MSEG_MKPF.VGABE = 'WE' THEN 'Warehouse Inbound for Purchase Order' WHEN MSEG_MKPF.VGABE = 'WQ' THEN 'Material Movement for Stock' WHEN MSEG_MKPF.VGABE = 'WR' THEN 'Material Movement after Manufacturing' ELSE 'Material Movement (other)' END AS Activity ,EKPO.MATNR AS Material -- <-- ,NULL AS StorageType ,MSEG_MKPF.LGORT AS StorageLocation ,SUBSTRING(MSEG_MKPF.CPUDT ,1,2) + '-' + SUBSTRING(MSEG_MKPF.CPUDT,4,2) + '-' + SUBSTRING(MSEG_MKPF.CPUDT,7,4) + ' ' + SUBSTRING(MSEG_MKPF.CPUTM,1,8) + '.0000' AS EventTime ,'020' AS Sorting ,MSEG_MKPF.USNAM AS EventUser ,EKBE.MATNR AS Material ,MSEG_MKPF.BWART AS MovementType ,MSEG_MKPF.MANDT AS Mandant FROM SAP.EKBE LEFT JOIN SAP.EKPO ON EKBE.MANDT = EKPO.MANDT AND EKBE.BUKRS = EKPO.BURKSEKBE.EBELN = EKPO.EBELN AND EKBE.Pos = EKPO.Pos LEFT JOIN SAP.MSEG_MKPF AS MSEG_MKPF -- <-- Here as a pre-join of MKPF & MSEG table ON EKBE.MANDT = MSEG_MKPF.MANDT AND EKBE.BURKS = MSEG.BUKRSMSEG_MKPF.MATNR = EKBE.MATNR AND MSEG_MKPF.EBELP = EKBE.EBELP WHERE EKBE.VGABE= '1' -- <-- OR EKBE.VGABE= '2' -- Warehouse Outbound -> VGABE = 1, Invoice Inbound -> VGABE = 2 |
Attention: Please see this SQL as a pure example of event mining for a classic (single table) event log! It is based on a German SAP ERP configuration with customized processes.
An Event Log can also include many other columns (attributes) that describe the respective process activity in more detail or the higher-level process context.
Incidentally, Process Mining can also work with more than just one timestamp per activity. Even the small Process Mining tool Fluxicon Disco made it possible to handle two activities from the outset. For example, when creating an order in the ERP system, the opening and closing of an input screen could be recorded as a timestamp and the execution time of the micro-task analyzed. This concept is continued as so-called task mining.
Task Mining
Task Mining is a subtype of Process Mining and can utilize user interaction data, which includes keystrokes, mouse clicks or data input on a computer. It can also include user recordings and screenshots with different timestamp intervals.
As Task Mining provides a clearer insight into specific sub-processes, program managers and HR managers can also understand which parts of the process can be automated through tools such as RPA. So whenever you hear that Process Mining can prepare RPA definitions you can expect that Task Mining is the real deal.
Machine Learning for Process and Task Mining on Text and Video Data
Process Mining and Task Mining is already benefiting a lot from Text Recognition (Named-Entity Recognition, NER) by Natural Lamguage Processing (NLP) by identifying events of processes e.g. in text of tickets or e-mails. And even more Task Mining will benefit form Computer Vision since videos of manufacturing processes or traffic situations can be read out. Even MTM analysis can be done with Computer Vision which detects movement and actions in video material.
Object-Centric Process Mining
Object-centric Process Data Modeling is an advanced approach of dynamic data modelling for analyzing complex business processes, especially those involving multiple interconnected entities. Unlike classical process mining, which focuses on linear sequences of activities of a specific process chain, object-centric process mining delves into the intricacies of how different entities, such as orders, items, and invoices, interact with each other. This method is particularly effective in capturing the complexities and many-to-many relationships inherent in modern business processes.
Note from the author: The concept and name of object-centric process mining was introduced by Wil M.P. van der Aalst 2019 and as a product feature term by Celonis in 2022 and is used extensively in marketing. This concept is based on dynamic data modelling. I probably developed my first event log made of dynamic data models back in 2016 and used it for an industrial customer. At that time, I couldn’t use the Celonis tool for this because you could only model very dedicated event logs for Celonis and the tool couldn’t remap the attributes of the event log while on the other hand a tool like Fluxicon disco could easily handle all kinds of attributes in an event log and allowed switching the event perspective e.g. from sales order number to material number or production order number easily.
An object-centric data model is a big deal because it offers the opportunity for a holistic approach and as a database a single source of truth for Process Mining but also for other types of analytical applications.
Enhancement of the Data Model for Obect-Centricity
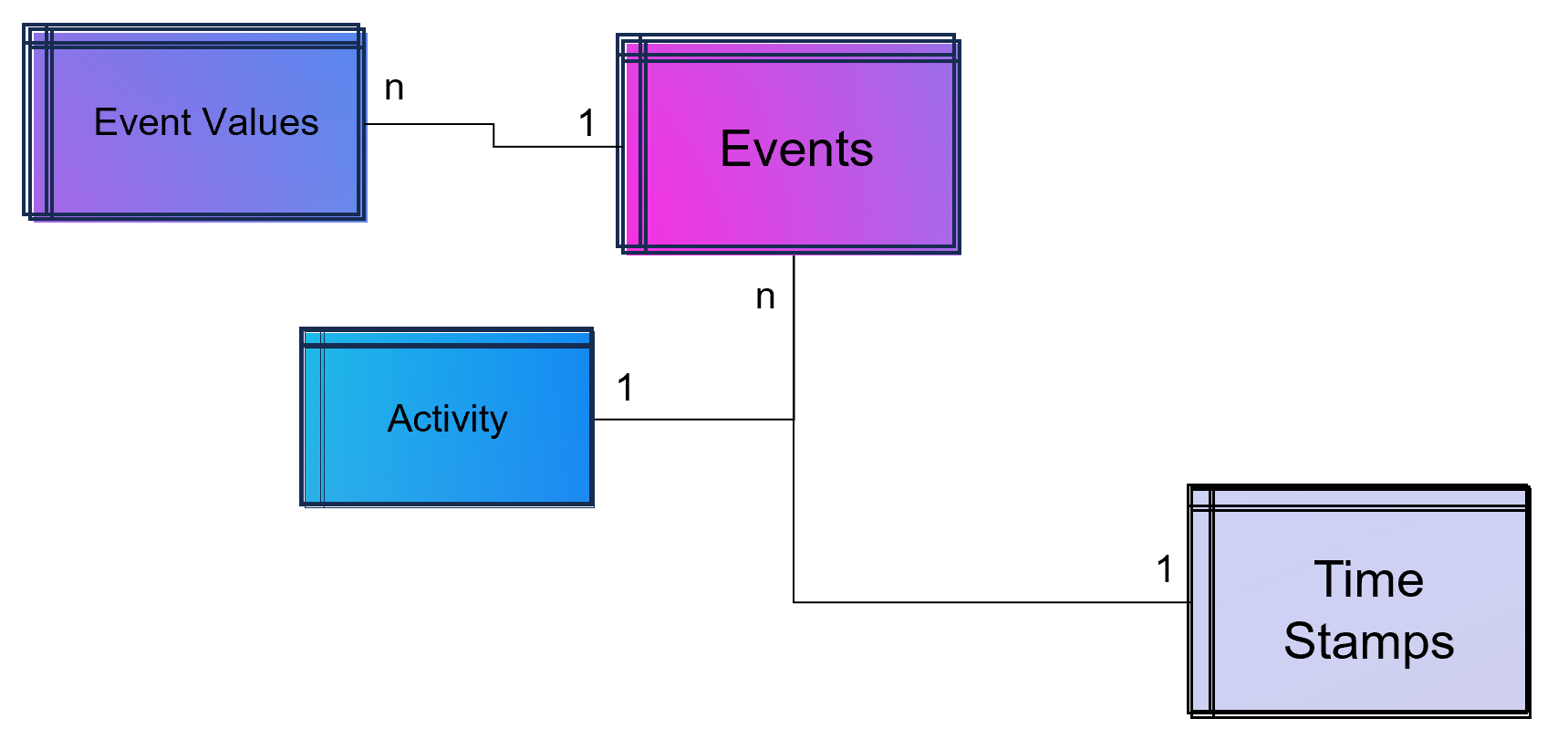
The Event Log is a data model that stores events and their related attributes. A classic Event Log has next to the Case ID, the timestamp and a activity description also process related attributes containing information e.g. about material, department, user, amounts, units, prices, currencies, volume, volume classes and much much more. This is something we can literally objectify!
The problem of this classic event log approach is that this information is transformed and joined to the Event Log specific to the process it is designed for.
An object-centric event log is a central data store for all kind of events mapped to all relevant objects to these events. For that reason our event log – that brings object into the center of gravity – we need a relational bridge table (Event_Object_Relation) into the focus. This tables creates the n to m relation between events (with their timestamps and other event-specific values) and all objects.
For fulfillment of relational database normalization the object table contains the object attributes only but relates their object attribut values from another table to these objects.

Advanced Event Log with dynamic Relations between Objects and Events
The above showed data model is already object-centric but still can become more dynamic in order to object attributes by object type (e.g. the type material will have different attributes then the type invoice or department). Furthermore the problem that not just events and their activities have timestamps but also objects can have specific timestamps (e.g. deadline or resignation dates).
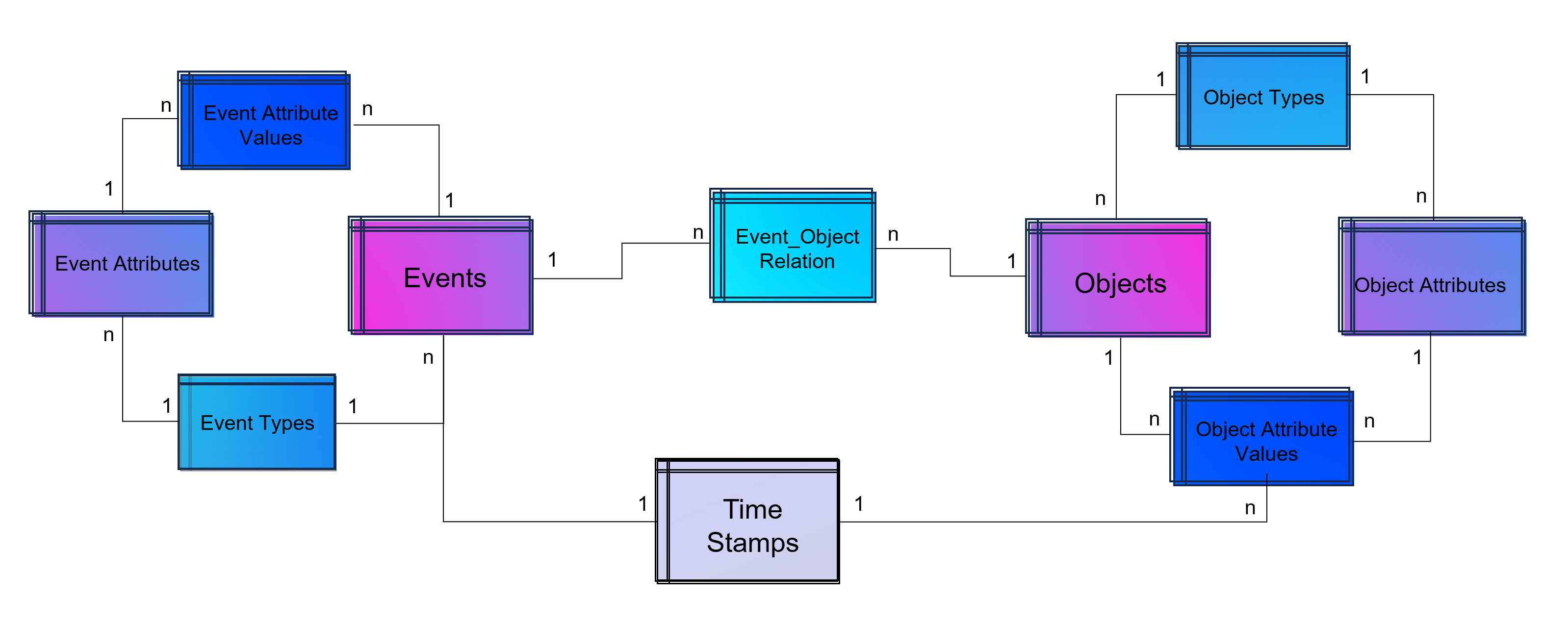
Advanced Event Log with dynamic Relations between Objects and Events and dynamic bounded attributes and their values to Events – And the same for Objects.
A last step makes the event log data model more easy to analyze with BI tools: Adding a classical time dimension adding information about each timestamp (by date, not by time of day), e.g. weekdays or public holidays.
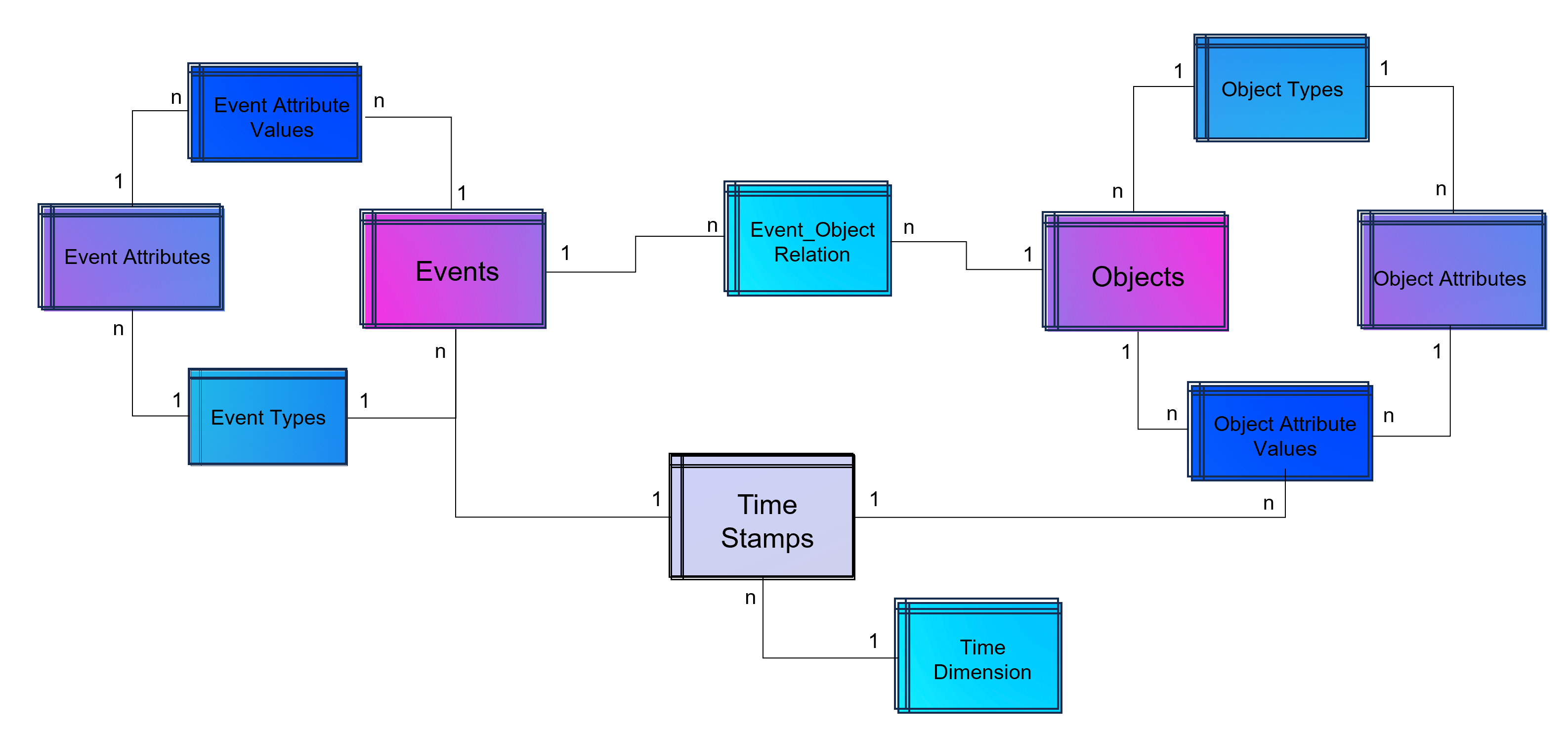
Advanced Event Log with dynamic Relations between Objects and Events and dynamic bounded attributes and their values to Events and Objects. The measured timestamps (and duration times in case of Task Mining) are enhanced with a time-dimension for BI applications.
For analysis the way of Business Intelligence this normalized data model can already be used. On the other hand it is also possible to transform it into a fact-dimensional data model like the star schema (Kimball approach). Also Data Science related use cases will find granular data e.g. for training a regression model for predicting duration times by process.
Note from the author: Process Mining is often regarded as a separate discipline of analysis and this is a justified classification, as process mining is essentially a graph analysis based on the event log. Nevertheless, process mining can be considered a sub-discipline of business intelligence. It is therefore hardly surprising that some process mining tools are actually just a plugin for Power BI, Tableau or Qlik.
Storing the Object-Centrc Analytical Data Model on Data Mesh Architecture
Central data models, particularly when used in a Data Mesh in the Enterprise Cloud, are highly beneficial for Process Mining, Business Intelligence, Data Science, and AI Training. They offer consistency and standardization across data structures, improving data accuracy and integrity. This centralized approach streamlines data governance and management, enhancing efficiency. The scalability and flexibility provided by data mesh architectures on the cloud are very beneficial for handling large datasets useful for all analytical applications.
Note from the author: Process Mining data models are very similar to normalized data models for BI reporting according to Bill Inmon (as a counterpart to Ralph Kimball), but are much more granular. While classic BI is satisfied with the header and item data of orders, process mining also requires all changes to these orders. Process mining therefore exceeds this data requirement. Furthermore, process mining is complementary to data science, for example the prediction of process runtimes or failures. It is therefore all the more important that these efforts in this treasure trove of data are centrally available to the company.
Central single source of truth models also foster collaboration, providing a common data language for cross-functional teams and reducing redundancy, leading to cost savings. They enable quicker data processing and decision-making, support advanced analytics and AI with standardized data formats, and are adaptable to changing business needs.
Central data models in a cloud-based Data Mesh Architecture (e.g. on Microsoft Azure, AWS, Google Cloud Platform or SAP Dataverse) significantly improve data utilization and drive effective business outcomes. And that´s why you should host any object-centric data model not in a dedicated tool for analysis but centralized on a Data Lakehouse System.
About the Process Mining Tool for Object-Centric Process Mining
Celonis is the first tool that can handle object-centric dynamic process mining event logs natively in the event collection. However, it is not neccessary to have Celonis for using object-centric process mining if you have the dynamic data model on your own cloud distributed with the concept of a data mesh. Other tools for process mining such as Signavio, UiPath, and process.science or even the simple desktop tool Fluxicon Disco can be used as well. The important point is that the data mesh approach allows you to easily generate classic event logs for each analysis perspective using the dynamic object-centric data model which can be used for all tools of process visualization…
… and you can also use this central data model to generate data extracts for all other data applications (BI, Data Science, and AI training) as well!
Data Literacy Day 2023 by StackFuel
/in Carrier, Certification / Training, Education / Certification, Events, Gerneral, Insights, Recommendations/by RedaktionDer Data Literacy Day 2023 findet am 7. November 2023 in Berlin oder bequem von zu Hause aus statt. Eine hybride Veranstaltung zum Thema Datenkompetenz.
Darum geht es bei der hybriden Daten-Konferenz.
Data Literacy ist heutzutage ein Must-have – beruflich wie privat. Seit 2021 wird Datenkompetenz von der Bundesregierung als unverzichtbares Grundwissen eingestuft. Doch der Umgang mit Daten will gelernt sein. Wie man Data Literacy in der deutschen Bevölkerung verankert und wie Bürger:innen zu Data Citizens werden, kannst Du am 7. November 2023 mit den wichtigsten Köpfen der Branche am #DLD23 im Basecamp Berlin oder online von zu Hause aus diskutieren.
Lerne von den Besten der Branche.
Am Data Literacy Day 2023 kommen führende Expert:innen aus den Bereichen Politik, Wirtschaft und Forschung zusammen.
In Diskussionen, Vorträgen und Roundtables sprechen wir über Initiativen, mit dessen Hilfe Datenkompetenzen flächendeckend über alle Berufs- und Gesellschaftsbereiche hinweg in Deutschland verankert werden.

Unser Data Science Blog Author, Gründer der DATANOMIQ und AUDAVIS, und Interim Head of Data, Benjamin Aunkofer, nimmt ebenfalls an diesem Event teil.
6 weitere Gründe, warum Du Dir jetzt ein Freiticket schnappen solltest.
- Hybrid-Teilnahme: Vor Ort in Berlin-Mitte oder online.
- Thematischer Fokus auf Deutschlands Datenzukunft.
- Expert:innen aus Politik, Wirtschaft und Wissenschaft sprechen über Data Literacy.
- Diskussion über Top-Initiativen in Deutschland, die bereits realisiert werden.
- Interaktiver Austausch mit Professionals in Roundtables und Netzwerkveranstaltungen.
- Der Eintritt zur Konferenz ist komplett kostenfrei.”
Das volle Programm kann hier direkt abgerufen werden: https://stackfuel.com/de/events/data-literacy-day-2023/
Über den Organisator, StackFuel:
StackFuel garantiert den Schulungserfolg mit bewährtem Trainingskonzept dank der Online-Lernumgebung. Ob im Data Science Onlinekurs oder Python-Weiterbildung, mit StackFuel lernen Studenten und Arbeitskräfte, wie mit Daten in der Wirklichkeit nutzbringend umgegangen und das volle Potenzial herrausgeholt werden kann.
Monitoring of Jobskills with Data Engineering & AI
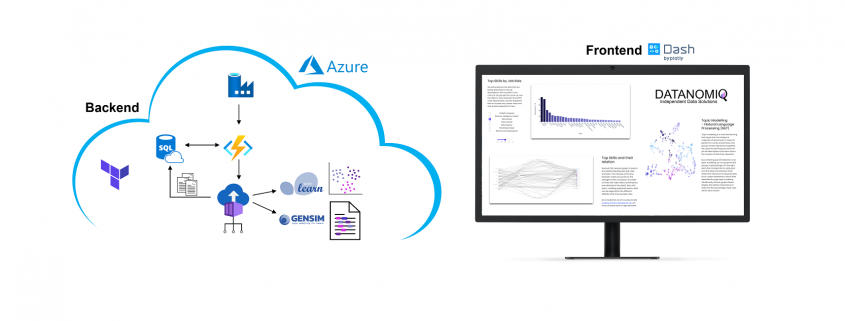
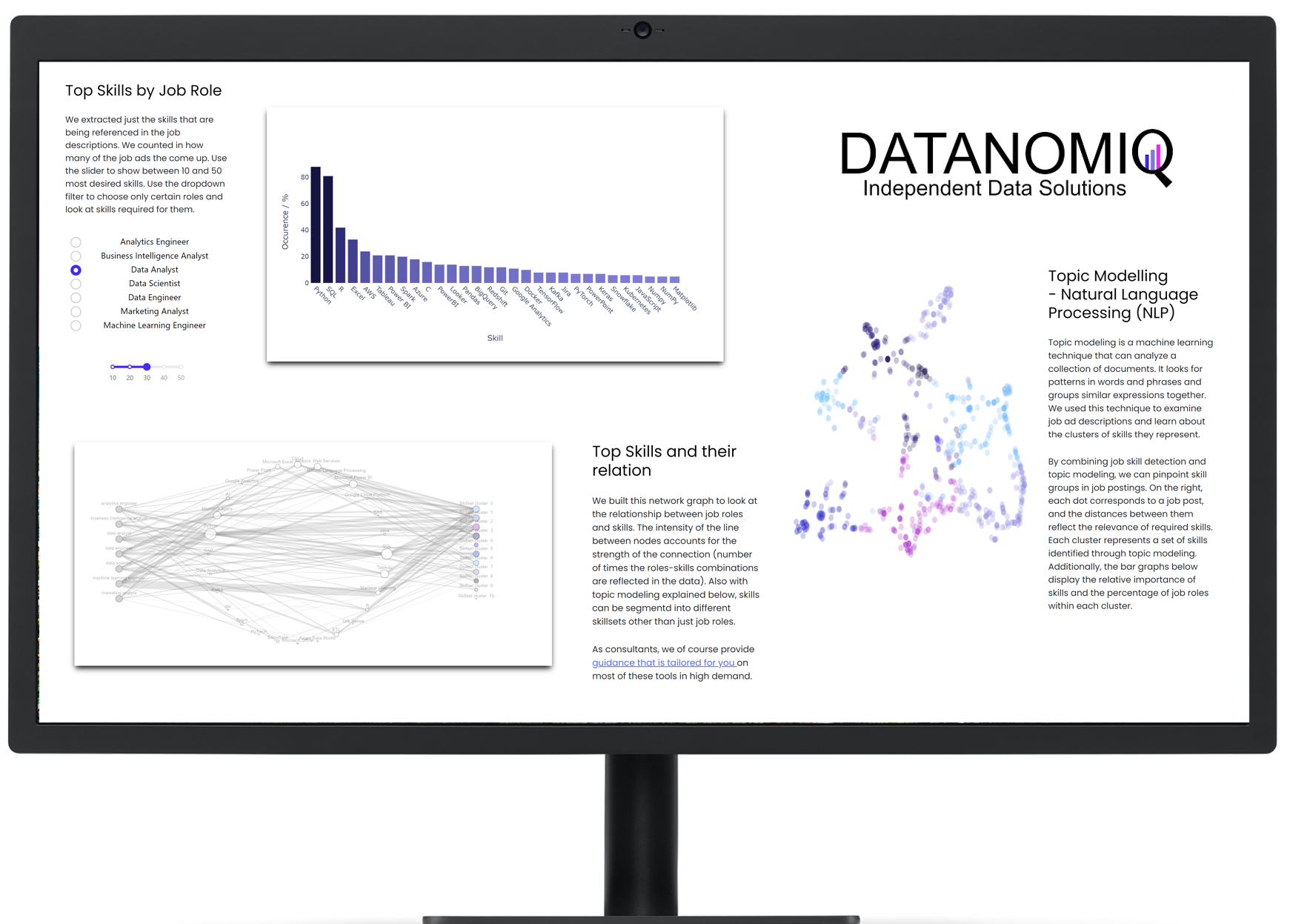
/in Artificial Intelligence, Business Intelligence, Carrier, Data Engineering, Data Mining, Data Science, Deep Learning, Gerneral, Insights, Machine Learning, Main Category, Natural Language Processing, Visualization/by Benjamin AunkoferOn own account, we from DATANOMIQ have created a web application that monitors data about job postings related to Data & AI from multiple sources (Indeed.com, Google Jobs, Stepstone.de and more).
The data is obtained from the Internet via APIs and web scraping, and the job titles and the skills listed in them are identified and extracted from them using Natural Language Processing (NLP) or more specific from Named-Entity Recognition (NER).
The skill clusters are formed via the discipline of Topic Modelling, a method from unsupervised machine learning, which show the differences in the distribution of requirements between them.
The whole web app is hosted and deployed on the Microsoft Azure Cloud via CI/CD and Infrastructure as Code (IaC).
The presentation is currently limited to the current situation on the labor market. However, we collect these over time and will make trends secure, for example how the demand for Python, SQL or specific tools such as dbt or Power BI changes.
Why we did it? It is a nice show-case many people are interested in. Over the time, it will provides you the answer on your questions related to which tool to learn! For DATANOMIQ this is a show-case of the coming Data as a Service (DaaS) Business.
Interesting links
Here are some interesting links for you! Enjoy your stay :)Pages
- @Data Science Blog
- authors
- Autor werden!
- Become an Author
- Bootcamp Datenanalyse und Maschinelles Lernen mit Python
- CIO Interviews
- Computational and Data Science
- Coursera Data Science Specialization
- Coursera 用Python玩转数据 Data Processing Using Python
- Data Leader Day 2016 – Rabatt für Data Scientists!
- Data Science
- Data Science Business Professional
- Data Science Insights
- Data Science Partner
- DATANOMIQ Big Data & Data Science Seminare
- DATANOMIQ Process Mining Workshop
- DATANOMIQ Seminare für Führungskräfte
- DataQuest.io – Interactive Learning
- Datenschutz
- Donation / Spende
- Education / Certification
- Fraunhofer Academy Zertifikatsprogramm »Data Scientist«
- Für Presse / Redakteure
- HARVARD Data Science Certificate Courses
- Home
- Impressum / Imprint
- MapR Big Data Expert
- Masterstudiengang Data Science
- Masterstudiengang Management & Data Science
- MongoDB University Online Courses
- Newsletter
- O’Reilly Video Training – Data Science with R
- Products
- qSkills Workshop: Industrial Security
- Science Digital Intelligence & Marketing Analytics
- Show your Desk!
- Stanford University Online -Statistical Learning
- Top Authors
- TU Chemnitz – Masterstudiengang Business Intelligence & Analytics
- TU Dortmund – Datenwissenschaft – Master of Science
- TU Dortmund berufsbegleitendes Zertifikatsstudium
- Weiterbildung mit Hochschulzertifikat Data Science & Business Analytics für Einsteiger
- WWU Münster – Zertifikatsstudiengang “Data Science”
- Zertifikatskurs „Data Science“
- Zertifizierter Business Analyst
Categories
- Apache Spark
- Artificial Intelligence
- Audit Analytics
- Big Data
- Books
- Business Analytics
- Business Intelligence
- Carrier
- Certification / Training
- Cloud
- Cloud
- Connected Car
- Customer Analytics
- Data Engineering
- Data Migration
- Data Mining
- Data Science
- Data Science at the Command Line
- Data Science Hack
- Data Science News
- Data Security
- Data Warehousing
- Database
- Datacenter
- Deep Learning
- Devices
- DevOps
- Education / Certification
- ETL
- Events
- Excel / Power BI
- Experience
- Gerneral
- GPU-Processing
- Graph Database
- Hacking
- Hadoop
- Hadoop Framework
- Industrie 4.0
- Infrastructure as Code
- InMemory
- Insights
- Interview mit CIO
- Interviews
- Java
- JavaScript
- Jobs
- Machine Learning
- Main Category
- Manufacturing
- Mathematics
- Mobile Device Management
- Mobile Devices
- Natural Language Processing
- Neo4J
- NoSQL
- Octave
- optimization
- Predictive Analytics
- Process Mining
- Projectmanagement
- Python
- Python
- R Statistics
- Re-Engineering
- Realtime Analytics
- Recommendations
- Reinforcement Learning
- Scala
- Software Development
- Sponsoring Partner Posts
- SQL
- Statistics
- TensorFlow
- Terraform
- Text Mining
- Tool Introduction
- Tools
- Tutorial
- Uncategorized
- Use Case
- Use Cases
- Visualization
- Web- & App-Tracking
Archive
- March 2025
- December 2024
- October 2024
- September 2024
- August 2024
- July 2024
- May 2024
- April 2024
- March 2024
- February 2024
- January 2024
- November 2023
- October 2023
- September 2023
- August 2023
- July 2023
- June 2023
- May 2023
- April 2023
- March 2023
- February 2023
- January 2023
- December 2022
- November 2022
- October 2022
- September 2022
- August 2022
- July 2022
- June 2022
- May 2022
- April 2022
- March 2022
- February 2022
- January 2022
- December 2021
- November 2021
- October 2021
- September 2021
- August 2021
- July 2021
- June 2021
- May 2021
- April 2021
- March 2021
- February 2021
- January 2021
- December 2020
- November 2020
- October 2020
- September 2020
- August 2020
- July 2020
- June 2020
- May 2020
- April 2020
- March 2020
- February 2020
- January 2020
- December 2019
- November 2019
- October 2019
- September 2019
- August 2019
- July 2019
- June 2019
- May 2019
- April 2019
- March 2019
- February 2019
- January 2019
- December 2018
- November 2018
- October 2018
- September 2018
- August 2018
- July 2018
- June 2018
- May 2018
- April 2018
- March 2018
- February 2018
- January 2018
- December 2017
- November 2017
- October 2017
- September 2017
- August 2017
- July 2017
- June 2017
- May 2017
- April 2017
- March 2017
- February 2017
- January 2017
- December 2016
- November 2016
- October 2016
- September 2016
- August 2016
- July 2016
- June 2016
- May 2016
- April 2016
- March 2016
- February 2016
- January 2016
- December 2015
- November 2015
- October 2015
- September 2015
- August 2015
- July 2015
- June 2015
- May 2015