Generative Adversarial Networks
After Deep Autoregressive Models, Deep Generative Modelling and Variational Autoencoders we now continue the discussion with Generative Adversarial Networks (GANs).
Introduction
So far, in the series of deep generative modellings (DGMs [Yad22a]), we have covered autoregressive modelling, which estimates the exact log likelihood defined by the model and variational autoencoders, which was variational approximations for lower bound optimization. Both of these modelling techniques were explicitly defining density functions and optimizing the likelihood of the training data. However, in this blog, we are going to discuss generative adversarial networks (GANs), which are likelihood-free models and do not define density functions explicitly. GANs follow a game-theoretic approach and learn to generate from the training distribution through a set up of a two-player game.

A two player model of GAN along with the generator and discriminators.
GAN tries to learn the distribution of high dimensional training data and generates high-quality synthetic data which has a similar distribution to training data. However, learning the training distribution is a highly complex task therefore GAN utilizes a two-player game approach to overcome the high dimensional complexity problem. GAN has two different neural networks (as shown in Figure ??) the generator and the discriminator. The generator takes a random input ![]() and produces a sample that has a similar distribution as
and produces a sample that has a similar distribution as ![]() . To train this network efficiently, there is the other network that is utilized as the second player and known as the discriminator. The generator network (player one) tries to fool the discriminator by generating real looking images. Moreover, the discriminator network tries to distinguish between real (training data
. To train this network efficiently, there is the other network that is utilized as the second player and known as the discriminator. The generator network (player one) tries to fool the discriminator by generating real looking images. Moreover, the discriminator network tries to distinguish between real (training data ![]() ) and fake images effectively. Our main aim is to have an efficiently trained discriminator to be able to distinguish between real and fake images (the generator’s output) and on the other hand, we would like to have a generator, which can easily fool the discriminator by generating real-looking images.
) and fake images effectively. Our main aim is to have an efficiently trained discriminator to be able to distinguish between real and fake images (the generator’s output) and on the other hand, we would like to have a generator, which can easily fool the discriminator by generating real-looking images.
Objective function and training
Objective function
Simultaneous training of these two networks is one of the main challenges in GANs and a minimax loss function is defined for this purpose. To understand this minimax function, firstly, we would like to discuss the concept of two sample testing by Aditya grover [Gro20]. Two sample testing is a method to compute the discrepancy between the training data distribution and the generated data distribution:
(1) ![]()
where
By combining Figure ?? and Equation 1, the first term ![]() corresponds to the discriminator, which has direct access to the training data and the second term
corresponds to the discriminator, which has direct access to the training data and the second term ![]() represents the generator part as it relies only on the latent space and produces synthetic data. Therefore, Equation 1 can be rewritten in the form of GAN’s two players as:
represents the generator part as it relies only on the latent space and produces synthetic data. Therefore, Equation 1 can be rewritten in the form of GAN’s two players as:
(2) ![]()
The above equation can be rearranged in the form of log loss:
(3) ![]()
In the above equation, the arguments are modified from ![]() and
and ![]() to
to ![]() and
and ![]() respectively as we would like to approximate the network parameters, which are represented by
respectively as we would like to approximate the network parameters, which are represented by ![]() and
and ![]() for the both generator and discriminator respectively. The discriminator wants to maximize the above objective for
for the both generator and discriminator respectively. The discriminator wants to maximize the above objective for ![]() such that
such that ![]() , which indicates that the outcome is close to the real data. Furthermore,
, which indicates that the outcome is close to the real data. Furthermore, ![]() should be close to zero as it is fake data, therefore, the maximization of the above objective function for
should be close to zero as it is fake data, therefore, the maximization of the above objective function for ![]() will ensure that the discriminator is performing efficiently in terms of separating real and fake data. From the generator point of view, we would like to minimize this objective function for
will ensure that the discriminator is performing efficiently in terms of separating real and fake data. From the generator point of view, we would like to minimize this objective function for ![]() such that
such that ![]() . If the minimization of the objective function happens effectively for
. If the minimization of the objective function happens effectively for ![]() then the discriminator will classify a fake data into a real data that means that the generator is producing almost real-looking samples.
then the discriminator will classify a fake data into a real data that means that the generator is producing almost real-looking samples.
Training
The training procedure of GAN can be explained by using the following visualization from Goodfellow et al. [GPAM+14]. In Figure 2(a), ![]() is a random input vector to the generator to produce a synthetic outcome
is a random input vector to the generator to produce a synthetic outcome ![]() (green curve). The generated data distribution is not close to the original data distribution
(green curve). The generated data distribution is not close to the original data distribution ![]() (dotted black curve). Therefore, the discriminator classifies this image as a fake image and forces generator to learn the training data distribution (Figure 2(b) and (c)). Finally, the generator produces the image which could not detected as a fake data by discriminator(Figure 2(d)).
(dotted black curve). Therefore, the discriminator classifies this image as a fake image and forces generator to learn the training data distribution (Figure 2(b) and (c)). Finally, the generator produces the image which could not detected as a fake data by discriminator(Figure 2(d)).
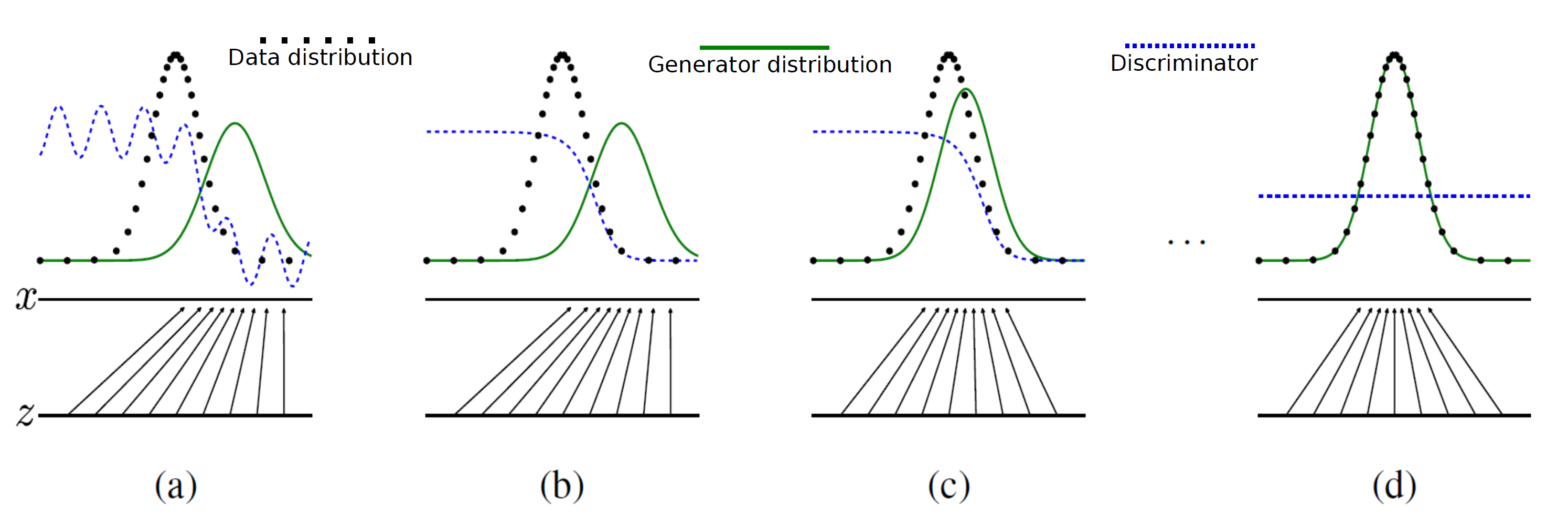
GAN’s training visualization: the dotted black, solid green lines represents pd and pθ
respectively. The discriminator distribution is shown in dotted blue. This image taken from Goodfellow
et al. [GPAM+14].
The optimization of the objective function mentioned in Equation 3 is performed in th following two steps repeatedly:
\begin{enumerate}
\item Firstly, the gradient ascent is utilized to maximize the objective function for ![]() for discriminator.
for discriminator.
(4) ![]()
\item In the second step, the following function is minimized for the generator using gradient descent.
(5) ![]()
\end{enumerate}
However, in practice the minimization for the generator does now work well because when ![]() then the term
then the term ![]() has the dominant gradient and vice versa.
has the dominant gradient and vice versa.
However, we would like to have the gradient behaviour completely opposite because ![]() means the generator is well trained and does not require dominant gradient values. However, in case of
means the generator is well trained and does not require dominant gradient values. However, in case of ![]() , the generator is not well trained and producing low quality outputs therefore, it requires a dominant gradient for an efficient training. To fix this problem, the gradient ascent method is applied to maximize the modified generator’s objective:
, the generator is not well trained and producing low quality outputs therefore, it requires a dominant gradient for an efficient training. To fix this problem, the gradient ascent method is applied to maximize the modified generator’s objective:
In the second step, the following function is minimized for the generator using gradient descent alternatively.
(6) ![]()
therefore, during the training, Equation 4 and 6 will be maximized using the gradient ascent algorithm until the convergence.
Results
The quality of the generated images using GANs depends on several factors. Firstly, the joint training of GANs is not a stable procedure and that could severely decrease the quality of the outcome. Furthermore, the different neural network architecture will modify the quality of images based on the sophistication of the used network. For example, the vanilla GAN [GPAM+14] uses a fully connected deep neural network and generates a quite decent result. Furthermore, DCGAN [RMC15] utilized deep convolutional networks and enhanced the quality of outcome significantly. Furthermore, different types of loss functions are applied to stabilize the training procedure of GAN and to produce high-quality outcomes. As shown in Figure 3, StyleGAN [KLA19] utilized Wasserstein metric [Yad22b] to generate high-resolution face images. As it can be seen from Figure 3, the quality of the generated images are enhancing with time by applying more sophisticated training techniques and network architectures.

GAN timeline with different variations in terms of network architecture and loss functions.
Summary
This article covered the basics and mathematical concepts of GANs. However, the training of two different networks simultaneously could be complex and unstable. Therefore, researchers are continuously working to create a better and more stable version of GANs, for example, WGAN. Furthermore, different types of network architectures are introduced to improve the quality of outcomes. We will discuss this further in the upcoming blog about these variations.
References
[GPAM+14] Ian Goodfellow, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, DavidWarde-Farley, Sherjil
Ozair, Aaron Courville, and Yoshua Bengio. Generative adversarial nets. Advances in
neural information processing systems, 27, 2014.
[Gro20] Aditya Grover. Generative adversarial networks.
https://deepgenerativemodels.github.io/notes/gan/, 2020.
[KLA19] Tero Karras, Samuli Laine, and Timo Aila. A style-based generator architecture for
generative adversarial networks. In Proceedings of the IEEE/CVF conference on computer
vision and pattern recognition, pages 4401–4410, 2019.
[RMC15] Alec Radford, Luke Metz, and Soumith Chintala. Unsupervised representation
learning with deep convolutional generative adversarial networks. arXiv preprint
arXiv:1511.06434, 2015.
[Yad22a] Sunil Yadav. Deep generative modelling. https://data-scienceblog.
com/blog/2022/02/19/deep-generative-modelling/, 2022.
[Yad22b] Sunil Yadav. Necessary probability concepts for deep learning: Part 2.
https://medium.com/@sunil7545/kl-divergence-js-divergence-and-wasserstein-metricin-
deep-learning-995560752a53, 2022.




 DATANOMIQ
DATANOMIQ
 https://www.haufe-akademie.de
https://www.haufe-akademie.de
Leave a Reply
Want to join the discussion?Feel free to contribute!