Deep Generative Modelling
Nowadays, we see several real-world applications of synthetically generated data (see Figure 1), for example solving the data imbalance problem in classification tasks, performing style transfer for artistic images, generating protein structure for scientific analysis, etc. In this blog, we are going to explore synthetic data generation using deep neural networks with the mathematical background.

Figure 1 – Synthetic images generated by deep generative models
What is Deep Generative modelling?
Deep generative modelling (DGM) falls in the category of unsupervised learning and addresses a challenging task of the distribution estimation of the given data. To approximate the underlying distribution of a complicated and high dimensional data, Deep generative models (DGM) utilize various deep neural networks architectures e.g., CNN and RNN. Furthermore, the trained DGMs generate samples which have the same distribution as the training data distribution. In other words, if the given training data has the distribution function 𝑝𝑑 (𝑥), then DGMs learn to
generate the samples from a distribution 𝑝𝜃 (𝑥) such that 𝑝𝑑 (𝑥) ≈ 𝑝𝜃 (𝑥).
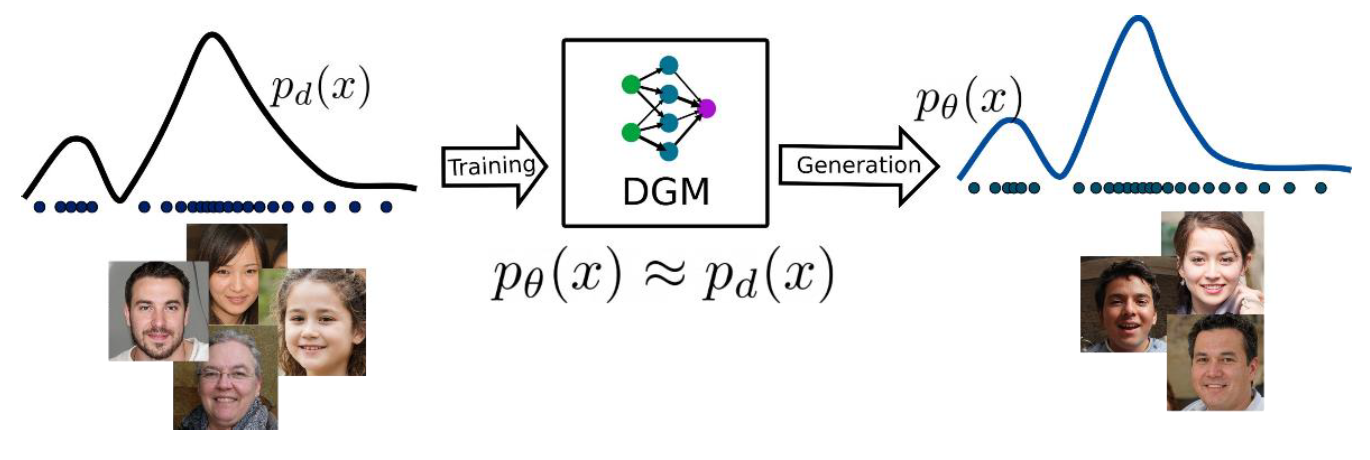
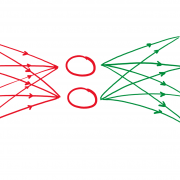
Figure 2 – DGMs pipeline
Figure 2 represents the general idea about the deep generative modeling, where DGMs are generating data samples with distribution of 𝑝𝜃 (𝑥), which is quite similar to the data distribution of training samples 𝑝𝑑 (𝑥).
Why Deep Generative modelling is important?
DGMs are mainly used to generate synthetic data, which can be used in different applications. The followings are a few examples:
- To avoid the data imbalance problems in several real-life classification problems
- Text-to-image, image-to-image conversion, image inpainting, super-resolution
- Speech and music synthesis.
- Computer graphics: rendering, texture generation, character movement, fluid dynamics
simulation.
How DGMs work?
The above figure is representing a complete workflow of DGMs and it is not very precise because it is combining both training and inference process. During the inference/generation, there will be a slight modification, which is shown in the following figure:
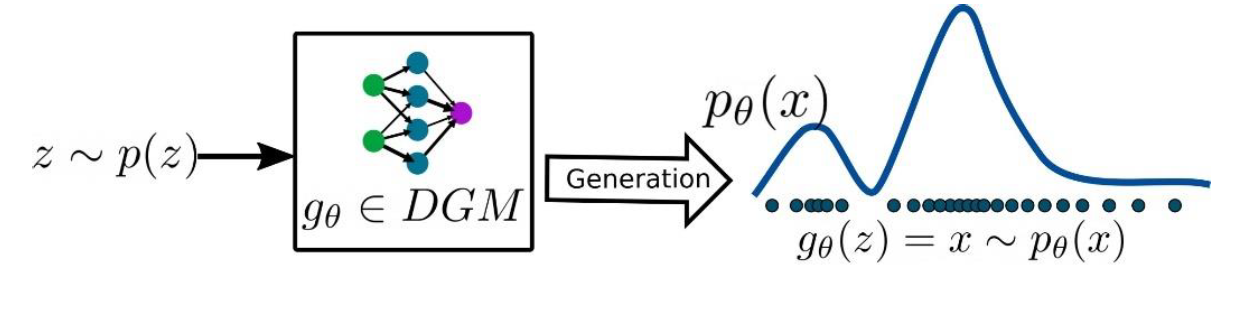
Figure 3 – Data generation with random input and a trained DGM
As it is clear from the above figure, the user gives a random sample as the input to the trained generator to generate a sample which has the similar distribution to the training data. Let us consider that the random input z is sampled from a tractable distribution 𝑝(𝑧) and supported in 𝑅𝑚 and the training data distribution (intractable) is high dimensional and supported in 𝑅𝑛. Therefore, the main goal of trained generator can be written as:
![]()
where d denotes the distance between the two probability distributions and every random vector z will mapped in an unknown vector x, which has an intractable distribution. The vector z is commonly referred as latent variable which is sample from a latent space and in general, follows a tractable Gaussian distribution. The distance minimization problem can be addressed using maximum likelihood. Let us assume that the generator function 𝑔𝜃 is known then we can compute the likelihood of the generated sample x from the latent variable z:
(1) ![]()
The term 𝑝𝜃(𝑥|𝑧) measures the closeness between the generated sample 𝑔𝜃(𝑧) to the original sample x. Based on the data, the likelihood function can be Gaussian for real valued data or Bernoulli for the binary data. From the above discussion, it is clear that the approximating the generator function is most challenging task and that is performed suing deep neural network with high dimensional data. A deep neural network approximates the generator function by computing the generator parameters 𝜃.
Types of DGMs
There are several different types of DGMs to approximate the generator functions, which can generate the new data points with the similar distribution of the training data. In this series of the blogs, we will discuss these methods which are mentioned in the following figure.
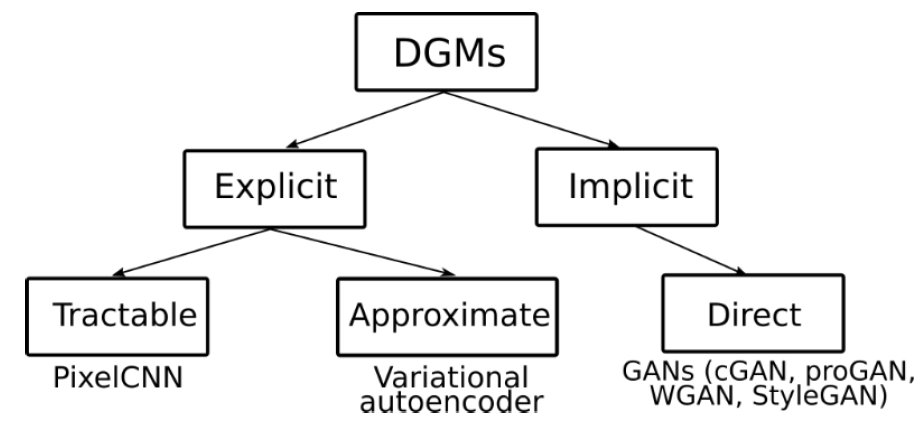
In general, DGMs can be separated into implicit and explicit methods, where explicit method are basically likelihood-based methods and learn the data distribution based on an explicitly defined 𝑝𝜃(𝑥). On the other hand, implicit methods learn data distribution directly without any prior model structure. Furthermore, explicit methods are split into tractable and approximation-based methods, where tractable methods are utilizing the model structures which have exact likelihood evaluation and approximation-based methods are applying different forms of approximation in the likelihood estimation.
Summary
In this blog article, we covered the mathematical foundation of DGMs including the different types. In further blog articles, we will cover the above mentioned different DGMs with theoretical background and applications.



Leave a Reply
Want to join the discussion?Feel free to contribute!