Variational Autoencoders
After Deep Autoregressive Models and Deep Generative Modelling, we will continue our discussion with Variational AutoEncoders (VAEs) after covering up DGM basics and AGMs. Variational autoencoders (VAEs) are a deep learning method to produce synthetic data (images, texts) by learning the latent representations of the training data. AGMs are sequential models and generate data based on previous data points by defining tractable conditionals. On the other hand, VAEs are using latent variable models to infer hidden structure in the underlying data by using the following intractable distribution function:
(1) ![]()
The generative process using the above equation can be expressed in the form of a directed graph as shown in Figure ?? (the decoder part), where latent variable ![]() produces meaningful information of
produces meaningful information of ![]() .
.
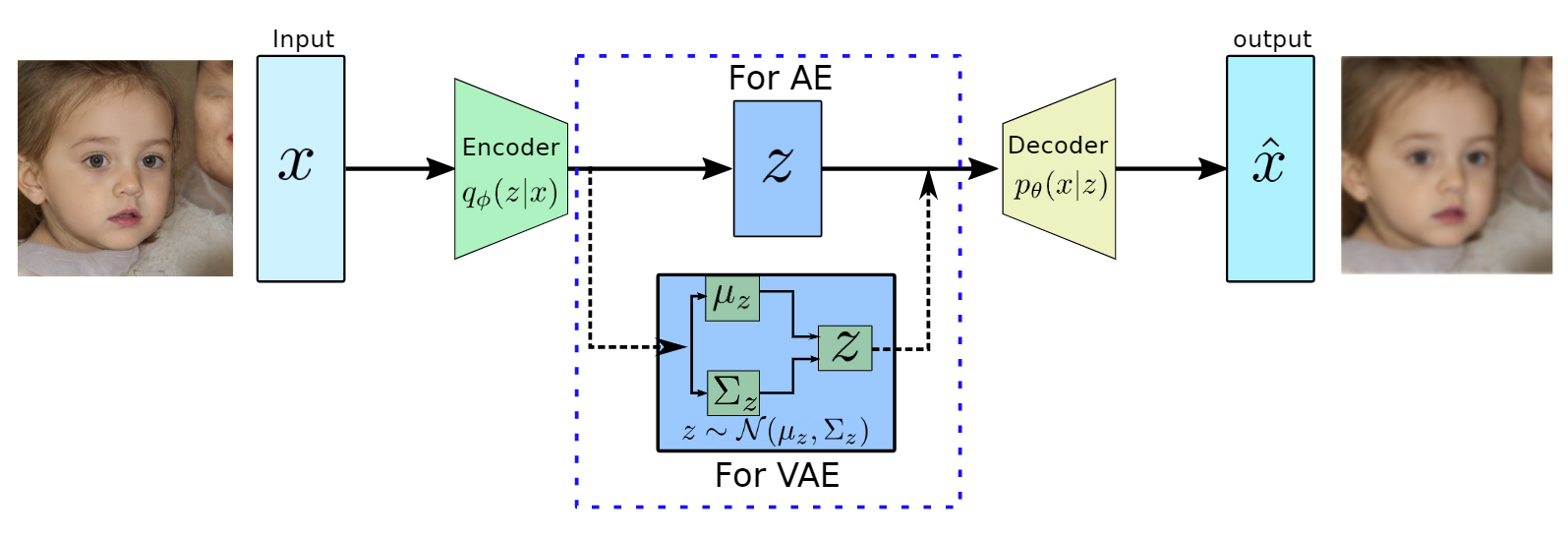
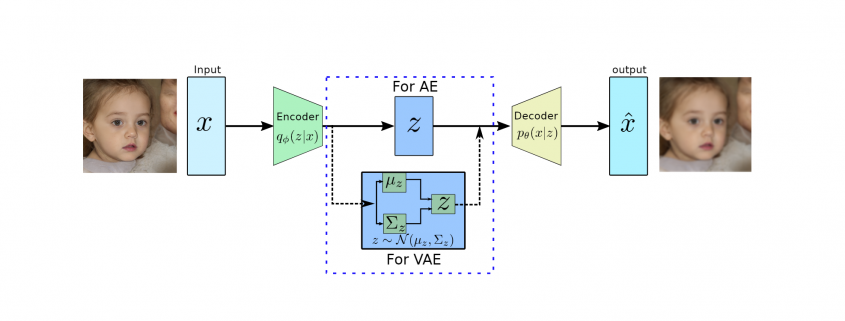
Figure 1: Architectures AE and VAE based on the bottleneck architecture. The decoder part work as
a generative model during inference.
Autoencoders
Autoencoders (AEs) are the key part of VAEs and are an unsupervised representation learning technique and consist of two main parts, the encoder and the decoder (see Figure ??). The encoders are deep neural networks (mostly convolutional neural networks with imaging data) to learn a lower-dimensional feature representation from training data. The learned latent feature representation ![]() usually has a much lower dimension than input
usually has a much lower dimension than input ![]() and has the most dominant features of
and has the most dominant features of ![]() . The encoders are learning features by performing the convolution at different levels and compression is happening via max-pooling.
. The encoders are learning features by performing the convolution at different levels and compression is happening via max-pooling.
On the other hand, the decoders, which are also a deep convolutional neural network are reversing the encoder’s operation. They try to reconstruct the original data ![]() from the latent representation
from the latent representation ![]() using the up-sampling convolutions. The decoders are pretty similar to VAEs generative models as shown in Figure 1, where synthetic images will be generated using the latent variable
using the up-sampling convolutions. The decoders are pretty similar to VAEs generative models as shown in Figure 1, where synthetic images will be generated using the latent variable ![]() .
.
During the training of autoencoders, we would like to utilize the unlabeled data and try to minimize the following quadratic loss function:
(2) ![]()
The above equation tries to minimize the distance between the original input and reconstructed image as shown in Figure 1.
Variational autoencoders
VAEs are motivated by the decoder part of AEs which can generate the data from latent representation and they are a probabilistic version of AEs which allows us to generate synthetic data with different attributes. VAE can be seen as the decoder part of AE, which learns the set parameters ![]() to approximate the conditional
to approximate the conditional ![]() to generate images based on a sample from a true prior,
to generate images based on a sample from a true prior, ![]() . The true prior
. The true prior ![]() are generally of Gaussian distribution.
are generally of Gaussian distribution.
Network Architecture
VAE has a quite similar architecture to AE except for the bottleneck part as shown in Figure 2. in AES, the encoder converts high dimensional input data to low dimensional latent representation in a vector form. On the other hand, VAE’s encoder learns the mean vector and standard deviation diagonal matrix such that ![]() as it will be performing probabilistic generation of data. Therefore the encoder and decoder should be probabilistic.
as it will be performing probabilistic generation of data. Therefore the encoder and decoder should be probabilistic.
Training
Similar to AGMs training, we would like to maximize the likelihood of the training data. The likelihood of the data for VAEs are mentioned in Equation 1 and the first term ![]() will be approximated by neural network and the second term
will be approximated by neural network and the second term ![]() prior distribution, which is a Gaussian function, therefore, both of them are tractable. However, the integration won’t be tractable because of the high dimensionality of data.
prior distribution, which is a Gaussian function, therefore, both of them are tractable. However, the integration won’t be tractable because of the high dimensionality of data.
To solve this problem of intractability, the encoder part of AE was utilized to learn the set of parameters ![]() to approximate the conditional
to approximate the conditional ![]() . Furthermore, the conditional
. Furthermore, the conditional ![]() will approximate the posterior
will approximate the posterior ![]() , which is intractable. This additional encoder part will help to derive a lower bound on the data likelihood that will make the likelihood function tractable. In the following we will derive the lower bound of the likelihood function:
, which is intractable. This additional encoder part will help to derive a lower bound on the data likelihood that will make the likelihood function tractable. In the following we will derive the lower bound of the likelihood function:
(3) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{flalign} \begin{aligned} log \: p_\theta (x) = & \mathbf{E}_{z\sim q_\phi(z|x)} \Bigg[log \: \frac{p_\theta (x|z) p_\theta (z)}{p_\theta (z|x)} \: \frac{q_\phi(z|x)}{q_\phi(z|x)}\Bigg] \\ = & \mathbf{E}_{z\sim q_\phi(z|x)} \Bigg[log \: p_\theta (x|z)\Bigg] - \mathbf{E}_{z\sim q_\phi(z|x)} \Bigg[log \: \frac{q_\phi (z|x)} {p_\theta (z)}\Bigg] + \mathbf{E}_{z\sim q_\phi(z|x)} \Bigg[log \: \frac{q_\phi (z|x)}{p_\theta (z|x)}\Bigg] \\ = & \mathbf{E}_{z\sim q_\phi(z|x)} \Big[log \: p_\theta (x|z)\Big] - \mathbf{D}_{KL}(q_\phi (z|x), p_\theta (z)) + \mathbf{D}_{KL}(q_\phi (z|x), p_\theta (z|x)). \end{aligned} \end{flalign} \end{equation*}](https://data-science-blog.com/wp-content/ql-cache/quicklatex.com-94567d6202e7ed5971ce2e83cbc2d369_l3.png)
In the above equation, the first line computes the likelihood using the logarithmic of
In the last line, the first term is representing the reconstruction loss and it will be approximated by the decoder network. This term can be estimated by the reparametrization trick \cite{}. The second term is KL divergence between prior distribution ![]() and the encoder function
and the encoder function ![]() , both of these functions are following the Gaussian distribution and has the closed-form solution and are tractable. The last term is intractable due to
, both of these functions are following the Gaussian distribution and has the closed-form solution and are tractable. The last term is intractable due to ![]() . However, KL divergence computes the distance between two probability densities and it is always positive. By using this property, the above equation can be approximated as:
. However, KL divergence computes the distance between two probability densities and it is always positive. By using this property, the above equation can be approximated as:
(4) ![]()
In the above equation, the term ![]() is presenting the tractable lower bound for the optimization and is also termed as ELBO (Evidence Lower Bound Optimization). During the training process, we maximize ELBO using the following equation:
is presenting the tractable lower bound for the optimization and is also termed as ELBO (Evidence Lower Bound Optimization). During the training process, we maximize ELBO using the following equation:
(5) ![]()
Furthermore, the reconstruction loss term can be written using Equation 2 as the decoder output is assumed to be following Gaussian distribution. Therefore, this term can be easily transformed to mean squared error (MSE).
During the implementation, the architecture part is straightforward and can be found here. The user has to define the size of latent space, which will be vital in the reconstruction process. Furthermore, the loss function can be minimized using ADAM optimizer with a fixed batch size and a fixed number of epochs.

Figure 2: The results obtained from vanilla VAE (left) and a recent VAE-based generative
model NVAE (right)
In the above, we are showing the quality improvement since VAE was introduced by Kingma and
Welling [KW14]. NVAE is a relatively new method using a deep hierarchical VAE [VK21].
Summary
In this blog, we discussed variational autoencoders along with the basics of autoencoders. We covered
the main difference between AEs and VAEs along with the derivation of lower bound in VAEs. We
have shown using two different VAE based methods that VAE is still active research because in general,
it produces a blurry outcome.
Further readings
Here are the couple of links to learn further about VAE-related concepts:
1. To learn basics of probability concepts, which were used in this blog, you can check this article.
2. To learn more recent and effective VAE-based methods, check out NVAE.
3. To understand and utilize a more advance loss function, please refer to this article.
References
[KW14] Diederik P Kingma and Max Welling. Auto-encoding variational bayes, 2014.
[VK21] Arash Vahdat and Jan Kautz. Nvae: A deep hierarchical variational autoencoder, 2021.





Leave a Reply
Want to join the discussion?Feel free to contribute!