Wie lernen Maschinen?
Im zweiten Teil wollen wir das mit Abstand am häufigsten verwendete Optimierungsverfahren – das Gradientenverfahren oder Verfahren des steilsten Abstiegs – anhand einiger Beispiele näher kennen lernen. Insbesondere werden wir sehen, dass die Suchrichtung, die bei der Benennung der Verfahren meist ausschlaggebend ist, gar nicht unbedingt die wichtigste Zutat ist.
Das Gradientenverfahren
Dieses Verfahren wird eigentlich in jedem Machine-Learning- oder Data-Science-Kurs wenigstens kurz beschrieben. Aber was genau tut es eigentlich, warum ist es so beliebt – oder genauer: so verbreitet?
Zunächst einmal muss man konstatieren, dass es das Gradientenverfahren so natürlich gar nicht gibt. Man meint hier ja nur die Festlegung der Suchrichtung auf den negativen Gradienten ![]() . Diese Wahl ist in einem bestimmten Sinne kanonisch und sogar optimal, dies wollen wir kurz beleuchten.
. Diese Wahl ist in einem bestimmten Sinne kanonisch und sogar optimal, dies wollen wir kurz beleuchten.
Der steilste Abstieg
Das Gradientenverfahren heißt auch Verfahren des steilsten Abstiegs – Steepest Descent im Englischen. Hier deutet sich die eben angesprochene Optimalität bereits an. Tatsächlich ist die Richtung des negativen Gradienten diejenige, die lokal – also in der unmittelbaren Umgebung des aktuellen Punktes – den größten Gewinn verspricht, man kann dies mathematisch rigoros beweisen. Durch diese Eigenschaft ist das Gradientenverfahren der Prototyp eines sog. Greedy-Algorithmus, der immer den unmittelbar größten Gewinn anstrebt. In der Praxis sind solche Greedy-Algorithmen vor allem wegen ihrer Einfachheit weit verbreitet. Im Fall des Gradientenverfahrens liegt die Einfachheit darin, dass die negative Gradientenrichtung immer eine Abstiegsrichtung ist, solange der Gradient ungleich Null ist, was ja ohnehin das erfolgreiche Ende unseres Algorithmus’ bedeuten würde. Der Test für eine Abstiegsrichtung ![]() war ja
war ja
Abstiegsrichtung: ![]()
und im Falle von ![]() vereinfacht sich das zu
vereinfacht sich das zu
![]()
Wir halten fest: Das Gradientenverfahren ist in Bezug auf die Suchrichtung an Einfachheit nicht zu überbieten, ein wichtiger Punkt für die Verbreitung einer Methode oder allgemeiner Technologie.
Um eine konkrete Vorstellung von der Arbeitsweise des Gradientenverfahrens zu bekommen, werden wir uns nun einige Beispiele anschauen.
Einige einfache Testfunktionen
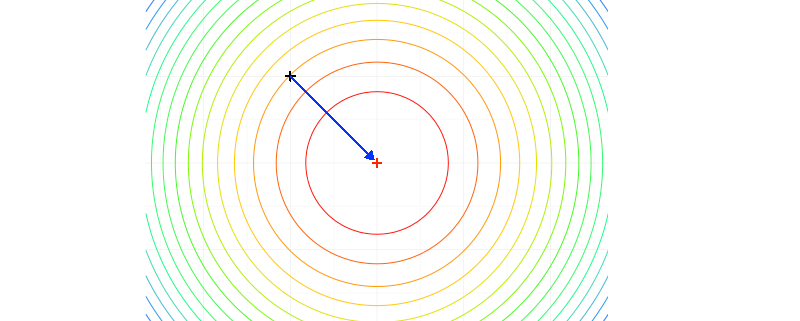
In diesem Abschnitt werden wir vier Funktionen kennenlernen, die uns helfen werden, die Stärken und Schwächen des Gradientenverfahrens kennenzulernen. Für jede der Funktionen wird ein sog. Contourplot für den zweidimensionalen Fall gezeigt, das ist eine Grafik, die die Höhenlinien einer Funktion enthält. Ein blauer Pfeil zeigt den kürzesten Weg zum Optimum – dargestellt als rotes Pluszeichen – und ein grauer Pfeil zeigt die tatsächliche Suchrichtung des Gradientenverfahrens.
Die Richtung des steilsten Abstiegs ist in vielen Fällen keine schlechte Idee, um dem gesuchten Optimum näherzukommen, wie unser erstes relativ triviales Beispiel zeigen wird. Die Funktion
![]()
beschreibt den halben quadratischen Abstand des Punktes ![]() vom Nullpunkt oder Ursprung
vom Nullpunkt oder Ursprung ![]() . Es ist eine sog. radiale Funktion, d.h. der Funktionswert hängt nur von der Norm des aktuellen Punktes ab und nicht von den konkreten Koordinaten. Damit handelt es sich im Wesentlichen um ein einfaches eindimensionales Optimierungsproblem und wir erwarten, dass unser Optimierungsverfahren dies in irgendeiner Form “bemerkt”.
. Es ist eine sog. radiale Funktion, d.h. der Funktionswert hängt nur von der Norm des aktuellen Punktes ab und nicht von den konkreten Koordinaten. Damit handelt es sich im Wesentlichen um ein einfaches eindimensionales Optimierungsproblem und wir erwarten, dass unser Optimierungsverfahren dies in irgendeiner Form “bemerkt”.
Die Höhenlinien sind in diesem Fall Kreise und die negative Gradientenrichtung stimmt mit der optimalen Suchrichtung überein – und zwar unabhängig vom Startpunkt. Tatsächlich bringt uns ein voller Gradientenschritt – die Schrittweite wäre dann 1 – direkt ans Ziel.
Die zweite Funktion ![]() ist komplizierter, es handelt sich um eine sog. anisotrope, d.h. richtungsabhängige Variante von
ist komplizierter, es handelt sich um eine sog. anisotrope, d.h. richtungsabhängige Variante von ![]() :
:
![]()
d.h. die Höhenlinien sind keine Kreise mehr, so dass sich der Funktionswert nicht nur mit der Länge, sondern auch mit der Richtung verändert. Diese Funktion ist ebenfalls noch relativ gutartig, aber das Gradientenverfahren tut sich unter Umständen bereits nicht mehr so leicht.
Die Höhenlinien sind nun elliptisch – und wir bemerken für den gewählten Punkt bereits eine gewisse Abweichung der Suchrichtung von der optimalen Richtung. Auffälliger noch als die Richtung ist aber die Länge des Gradienten, ein voller Schritt mit Schrittweite 1 würde zu einer deutlichen Verschlechterung führen, so dass bereits mehrere Schrittweiten getestet werden müssten, um einen akzeptablen Schritt zu finden, was wiederum mit Aufwand verbunden ist.
Die dritte Funktion
![]()
ist wiederum eine einfache symmetrische Funktion, und auf den ersten Blick erwartet man vielleicht ein ähnliches Verhalten wie bei ![]() .
.
Die Höhenlinien sehen aus wie Quadrate mit abgerundeten Ecken, und wiederum kann der negative Gradient deutlich von der besten Suchrichtung abweichen.
Die letzte und mit Abstand interessanteste Funktion ist eine Variante der sog. Rosenbrock-Funktion, der wahrscheinlich bekanntesten Testfunktion der mathematischen Optimierung:
![]() ,
,
eine Standardwahl für die Parameter wäre etwa ![]() und
und ![]() (die Definition für
(die Definition für ![]() Dimensionen entnehme man obigem Link). Die Rosenbrock-Funktion heißt auch Rosenbrock’s Banana Function und zeichnet sich durch einen für das Gradientenverfahren ungünstigen, speziell gekrümmten Verlauf der Höhenlinien aus.
Dimensionen entnehme man obigem Link). Die Rosenbrock-Funktion heißt auch Rosenbrock’s Banana Function und zeichnet sich durch einen für das Gradientenverfahren ungünstigen, speziell gekrümmten Verlauf der Höhenlinien aus.
Da die Suchrichtung in diesem Fall extrem ungünstig ist, werden hier nur sehr kurze Schritte zu einer Verbesserung führen, d.h. der Algorithmus muss sehr viele sehr kleine Schritte machen, um das Optimum zu erreichen.
Die Höhenlinien beschreiben eine Form, die der einer Banane nicht unähnlich ist, und diese Krümmung macht es auch anderen Optimierungsverfahren im allgemeinen sehr schwer, eine gute Suchrichtung zu finden. Dem/der aufmerksamen Leser/in ist vielleicht bereits aufgefallen, dass die hier gewählten Parameter von den oben angegebenen abweichen. Dies liegt ganz einfach daran, dass der Verlauf der Höhenlinien bei dieser Wahl bereits so extrem ist, dass sich das mit einem einfachen Contour Plot gar nicht mehr angemessen darstellen lässt, insbesondere die Form der Täler kann nicht mehr erkannt werden. Zum Vergleich betrachte man den Plot mit dieser Parameterwahl, die Höhenlinien sehen aus wie Ellipsen und die hochgradige Irregularität dieser Funktion ist nicht mehr zu erkennen.
Hier ist besonders gut erkennbar, dass die negative Gradientenrichtung für komplizierte Funktionen eine sehr ungünstige Wahl sein kann, obwohl sie lokal sogar optimal ist, eine typische Eigenschaft vieler “Greedy”-Algorithmen.
Nun wollen wir uns aber dem – zumindest in meinen Augen – heimlichen “Chef” vieler Optimierungsverfahren zuwenden.
Der Einfluss der Schrittweite
Noch einmal kurz zum Verständnis der Schrittweite an sich. Diese regelt in etwa die lokale Reichweite des Verfahrens. Sind wir hier zu restriktiv und bevorzugen kurze bis sehr kurze Schrittweiten, so wird das Verfahren insgesamt sehr viele Schritte benötigen, da wir uns ja in jedem Schritt dem angstrebten Optimum nur so weit nähern können, wie die Schrittweite erlaubt. Daher ist es wichtig, zumindest in bestimmten Situationen große Schritte zuzulassen, wir werden noch ein Beispiel dafür sehen und auch, welchen Einfluss man damit nehmen kann.
Exakt oder inexakt
Grundsätzlich unterscheidet man zwischen exakten und inexakten Schrittweiten. Exakt Schrittweiten versuchen, in der gegebenen Suchrichtung ein Minimum zu finden, d.h. die Funktion entlang der Suchrichtung exakt zu minimieren. Solche Methoden sind manchmal notwendig, um bestimmte theoretische Eigenschaften zu garantieren. In der Praxis haben sich aber die inexakten Methoden bewährt und durchgesetzt. Diese begnügen sich mit dem Erreichen eines bestimmten “ausreichenden” Abstiegs, was im Wesentlichen zwei große Vorteile besitzt. Zum einen lässt sich das exakte Minimum entlang der Suchrichtung, also die exakte Schrittweite, meist nur mit relativ hohem Aufwand bestimmen – hier muss ja ein komplettes Optimierungsproblem gelöst werden, wenn auch nur in einer Dimension. Zum anderen sind wir ja gar nicht an der Optimallösung in dieser einen Richtung interessiert, sondern am Optimum im kompletten Suchraum, so dass das Ergebnis der eindimensionalen exakten Schrittweitensuche oft “überoptimiert” oder überangepasst ist, ganz im Sinne des aus dem Machine-Learning-Kontext bereits bekannten Overfitting. Die exakte Schrittweite ist dann zwar für die gewählte Suchrichtung optimal, für das insgesamt zu lösende Problem aber zu speziell. Inexakte Schrittweiten stellen also in der Regel eine Win-Win-Situation dar, schnellere und einfachere Berechnung bei gleichzeitig besserer Performance, da Overfitting vermieden wird.
Die Armijo-Regel
Wir haben eine Standardwahl der Schrittweite – die Armijo-Regel – bereits in Wie lernen Maschinen Teil 1 kennengelernt. Theoretisch kann man das Gradientenverfahren auch mit einer sehr kleinen festen Schrittweite durchführen, aber davon ist in quasi jedem Fall abzuraten, es handelt sich hierbei einfach um eine sehr schlechte Schrittweitensteuerung, die zu einer teils extrem großen Zahl an Iterationsschritten führt, siehe unten.
Wenn wir die Performance eines Optimierungsverfahrens angemessen beurteilen wollen, so müssen wir uns mit vor allem mit der Schrittweitensteuerung beschäftigen. Nur die Kombination aus Suchrichtung und passender Schrittweite macht ein Verfahren erfolgreich, und selbst sehr gute Methoden – bezogen auf die Wahl der Suchrichtung – kann man durch eine ungeschickte, in der Regel zu restriktive Wahl der Schrittweite “ruinieren”. Umgekehrt kann man durch minimale Änderungen bereits sehr große Verbesserungen erreichen, wir werden im Folgenden versuchen, dies angemessen zu dokumentieren.
Weitere Einflussfaktoren
Zunächt muss man feststellen, dass ein komplettes algorithmisches Setup eine Vielzahl von Parametern umfasst.
Als Abbruchbedingung – wir sind “nah genug” an einem lokalen Optimum – verwenden wir die Toleranz ![]() , d.h. das Verfahren wird erfolgreich beendet, wenn die Norm des Gradienten kleiner als
, d.h. das Verfahren wird erfolgreich beendet, wenn die Norm des Gradienten kleiner als ![]() ist.
ist.
Darüberhinaus spielt der Startpunkt eine nicht zu unterschätzende Rolle, insbesondere das Gradientenverfahren ist hier sensitiv. Um dies zu illustrieren, werden wir für die folgenden Test unterschiedliche Starttpunkte verwenden. Für die ersten drei Textfunktionen ist das globale Minimum jeweils der Nullpunkt ![]() . Wir probieren in den weiteren Tests drei verschiedene Startpunkte aus, unter der Ergebnis-Tabelle findet sich immer der Verweis auf den jeweils gewählten Startpunkt. Die Wahl der Punkte ist nicht zufällig, die Benennung wird dies verdeutlichen.
. Wir probieren in den weiteren Tests drei verschiedene Startpunkte aus, unter der Ergebnis-Tabelle findet sich immer der Verweis auf den jeweils gewählten Startpunkt. Die Wahl der Punkte ist nicht zufällig, die Benennung wird dies verdeutlichen.
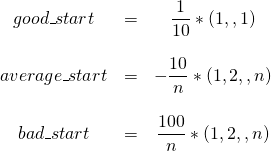
Mit ![]() ist die Problemdimension gemeint. Die weiter oben angegebenen Funktionen lassen sich auf kanonische Weise verallgemeinern für mehr als zwei Dimensionen, und wir wollen natürlich auch verstehen, wie unsere Optimierungsverfahren “skalieren”, wenn die Problemgröße wächst.
ist die Problemdimension gemeint. Die weiter oben angegebenen Funktionen lassen sich auf kanonische Weise verallgemeinern für mehr als zwei Dimensionen, und wir wollen natürlich auch verstehen, wie unsere Optimierungsverfahren “skalieren”, wenn die Problemgröße wächst.
Die Rosenbrock-Funktion ist ein wenig spezieller und erfordert eine andere Wahl, das – oder besser: ein – Minimum befindet sich bei ![]() . Wir wählen hier als Startpunkte
. Wir wählen hier als Startpunkte
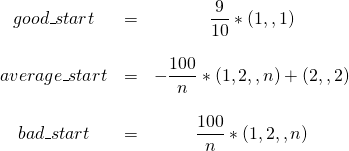
Test 1 – Der Einfluss der Dimensionalität
Um ein Gefühl für die Problemstellungen oder “Rahmenbedingungen” der mathematischen Optimierung und damit auch des Machine Learnings zu bekommen, betrachten wir zunächst einmal das Standard-Lehrbuch-Gradientenverfahren mit der Armijo-Regel als Schrittweitensteuerung.
Das triviale, effektiv eindimensionale Optimierungsproblem ![]() zeigt das ideale Verhalten. Das Verfahren ist für unsere Parameterwahl perfekt, es löst das Problem in einer konstanten Anzahl Schritte, völlig unabhängig von der Dimension.
zeigt das ideale Verhalten. Das Verfahren ist für unsere Parameterwahl perfekt, es löst das Problem in einer konstanten Anzahl Schritte, völlig unabhängig von der Dimension.
Das zweite Problem zeigt dagegen ein ungünstiges Verhalten, die Anzahl der Iterationen skaliert quadratisch mit der Dimension – die Anzahl der Iterationen, Funktions- und Gradientenauswertungen wächst bei einer Verdopplung der Dimension ungefähr mit dem Faktor ![]() . Solch eine Skalierung limitiert die Anwendbarkeit eines Verfahrens erheblich, in der Praxis benötigt man lineare Skalierung, eventuell mit logarithmischen Faktoren, eine angemessene Diskussion würde den Rahmen allerdings sprengen.
. Solch eine Skalierung limitiert die Anwendbarkeit eines Verfahrens erheblich, in der Praxis benötigt man lineare Skalierung, eventuell mit logarithmischen Faktoren, eine angemessene Diskussion würde den Rahmen allerdings sprengen.
Die dritte Funktion zeigt ein “gutes” Skalierungverhalten, es ist sublinear, bei einer Verdopplung der Problemgröße wächst die Anzahl der Iterationen etc. nur um einen Faktor von ca. ![]() .
.
Das vierte Problem, mathematisch eigentlich das kniffligste, zeigt ein überraschend harmloses Verhalten, eine ebenfalls konstante Skalierung, aber wir haben bewusst den “guten” Startpunkt gewählt.
Die Laufzeiten vergrößern sich natürlich auch bei konstanter Skalierung, da die Berechnung eines Iterationsschrittes ja mit wachsender Dimension aufwendiger wird aufgrund der höheren Anzahl arithmetischer Operationen, hierauf liegt aber nicht unser Fokus.
Test 2 – Ein erster Vergleich
Nun wollen wir einmal die beiden bisher angesprochenen Schrittweiten – die Armijo-Regel und die exakte Schrittweite in einem Praxistest nebeneinanderstellen.
Wir wir sehen, sehen wir nichts – Definitives. Es sei noch gesagt, dass Gradientenauswertungen in der Regel wesentlich teurer sind als Funktionsauswertungen, so dass die exakte Schrittweite – hier als Bisektionsverfahren implementiert – von den Laufzeiten her ohnehin nicht konkurrenzfähig ist. Wir sind hier jedoch an einem eher qualitativen Vergleich interessiert und wollen demonstrieren, dass die exakte Schrittweite zu schlechteren Ergebnissen – höhere Anzahl Iterationschritte, das angesprochene “Overfitting” – führen kann als eine einfache inexakte Schrittweite.
Test 3 – Ein weiterführender Vergleich
Nun wollen wir den Einfluss der Schrittweite besser verstehen lernen. Dazu betrachten wir neben der Armijo-Schrittweite und der exakten Schrittweite – dem Optimum in der gewählten Suchrichtung – noch eine minimale Variation der Armijo-Regel, die sog. Armijo-Regel mit Aufweitun. Diese Variante erlaubt größere Schrittweiten, da im Falle eines erfolgreichen Tests der Armijo-Bedingung für ![]() noch zusätzlich versucht wird, die Schrittweite zu verdoppeln, solange die Armijo-Bedingung erfüllt bleibt (d.h. man testet nicht nur
noch zusätzlich versucht wird, die Schrittweite zu verdoppeln, solange die Armijo-Bedingung erfüllt bleibt (d.h. man testet nicht nur ![]() , sondern u.U. auch
, sondern u.U. auch ![]() ).
).
Algorithmisch ist dies eine minimale Änderung, wir werden sehen, was das in der Praxis bedeutet oder bedeuten kann.
Für diesen Test wollen wir uns eine Aufälligkeit aus den ersten Tests näher anschauen. Das Gradientenverfahren mit Armijo-Regel hat bei der Minimierung der relativ einfachen Funktion ![]() erstaunlich schlecht abgeschnitten, während die exakte Schrittweite in Test 1 hier “glänzen” konnte.
erstaunlich schlecht abgeschnitten, während die exakte Schrittweite in Test 1 hier “glänzen” konnte.
Das Ergebnis mag auf den ersten Blick überraschen, aber es illustriert das Potential, welches an dieser Stelle verborgen liegt: Eine triviale minimale Veränderung der Schrittweitensteuerung reduziert die Komplexität vom worst case zum best case.
der tiefere Grund, warum das Gradientenverfahren mit Armijo-Regel hier so schlecht war, liegt darin, dass die Suchrichtung gut ist, die Länge eines vollen Gradientenschrittes aber zumindest in der relativen Nähe des Optimums sehr kurz ist. Dieses Missverhältnis lässt sich durch die Idee der Aufweitung beheben.
Test 4 – Der Härtetest
Zuguterletzt wollen wir die verschiedenen Schrittweitenstrategien anhand der Rosenbrock-Funktion testen, die insbesondere für das Gradientenverfahren sehr schwierig ist, als Parameter wählen wir ![]() . In solch einem hard case würden wir erwarten, dass die Schrittweitensteuerung generell wenig retten kann, wenn bereits die Suchrichtung erwiesenermaßen schlecht ist, was – wie weiter oben bereits besprochen – dann zu vielen sehr kurzen Schritten führt. Insbesondere eine Variante, die die Schritte zu verlängern sucht, erscheint hier nicht unbedingt als gute Idee. Sehen wir selbst:
. In solch einem hard case würden wir erwarten, dass die Schrittweitensteuerung generell wenig retten kann, wenn bereits die Suchrichtung erwiesenermaßen schlecht ist, was – wie weiter oben bereits besprochen – dann zu vielen sehr kurzen Schritten führt. Insbesondere eine Variante, die die Schritte zu verlängern sucht, erscheint hier nicht unbedingt als gute Idee. Sehen wir selbst:
In Dimension ![]() sieht alles in etwa wie erwartet aus, Aufweitung kommt überhaupt nur einmal vor und bewirkt quasi nichts. Aber in Dimension
sieht alles in etwa wie erwartet aus, Aufweitung kommt überhaupt nur einmal vor und bewirkt quasi nichts. Aber in Dimension ![]() sehen wir einen überraschenden Effekt. Bereits drei(!) Aufweitungen genügen – einmal alle
sehen wir einen überraschenden Effekt. Bereits drei(!) Aufweitungen genügen – einmal alle ![]() Schritte – um eine signifikante Beschleunigung im zweistelligen Prozentbereich zu bewirken.
Schritte – um eine signifikante Beschleunigung im zweistelligen Prozentbereich zu bewirken.
Zusammenfassung
Wir haben anhand einiger Beispiele gesehen, dass die Schrittweite eine wesentliche Auswirkung auf die Performance eines Algorithmus’ hat. Dies gilt umso mehr im Machine-Learning-Umfeld, wo die zu minimierenden Funktionen oftmals nichtlinear sind und durchaus gewisse konzeptionelle Ähnlichkeiten mit den hier verwendeten prototypischen Beispielfunktionen haben. Wir konnten hier nur einen kleinen Ausschnitt der Thematik beleuchten, aber wer Interesse hat, kann sich den verwendeten R-Code bei github herunterladen und einmal selber ausprobieren. Dort finden sich auch weitere Informationen rund um das Thema.
Fixed stepsize
Einen letzter Kommentar zur Wahl einer kleinen festen Schrittweite: Oftmals findet man Beschreibungen des Gradientenverfahrens ohne Schrittweitensteuerung, etwa in der englischsprachigen Wikipedia. In der Theorie funktioniert dies, solange die Schrittweite klein genug ist, aber dies ist ein ausschließlich theoretisch relevantes Resultat. Der minimale Aufwand, der mit der Auswahl einer Schrittweite einhergeht, zahlt sich quasi immer aus und beschleunigt das Verfahren um ein Vielfaches. Wer das einmal selbst sehr plastisch erfahren möchte, der folge den Anweisungen in dieser Readme. Wer genug Zeit mitbringt und darüberhinaus Spaß an solchen Dingen hat, der versuche einmal, die Funktion ![]() in Dimension
in Dimension ![]() für den Startpunkt
für den Startpunkt ![]() in weniger als 1 Million Iterationsschritten zu minimieren – ohne die Toleranz
in weniger als 1 Million Iterationsschritten zu minimieren – ohne die Toleranz ![]() zu verändern.
zu verändern.
Es ist jetzt doch ein langer Blogpost geworden, aber wir hoffen, zumindest das Potential, welches hier – im Untergrund der eigentlichen Machine-Learning-Verfahren – verborgen liegt, aufgezeigt haben zu können. Als weiterführende Themen würden sich moderne Verfahren wie die Methode der konjugierten Gradienten oder Quasi-Newton-Verfahren anbieten, außerdem natürlich ausgefeiltere Methoden zur Bestimmung von Schrittweiten wie Wolfe-Powell etc. Es wird weiterhin genug zu lernen geben, für Mensch und Maschine.
Vorheriger Artikel: Wie Lernen Maschinen? Teil 1.















Trackbacks & Pingbacks
[…] der kleinsten Fehlerquadrate und hat mehr als eine mathematische Methode zur Lösungsfindung (Gradientenverfahren und Normalengleichung). Wir wollen uns in diesem Artikel nicht auf die Mathematik konzentrieren, […]
[…] der kleinsten Fehlerquadrate und hat mehr als eine mathematische Methode zur Lösungsfindung (Gradientenverfahren und Normalengleichung). Wir wollen uns in diesem Artikel nicht auf die Mathematik konzentrieren, […]
[…] in der Regel nicht auf Anhieb, sie müssen unter Einsatz von Optimierungsverfahren, wie der Gradientenmethode, verbessert werden. Ein Data Scientist muss Unter- und Überanpassung erkennen können und er muss […]
[…] in der Regel nicht auf Anhieb, sie müssen unter Einsatz von Optimierungsverfahren, wie der Gradientenmethode, verbessert werden. Ein Data Scientist muss Unter- und Überanpassung erkennen können und er muss […]
[…] zweiten Grades in den Variablen . Es gibt daher strukturelle Ähnlichkeiten zu einigen der im zweiten Teil vorgestellten Testfunktionen, aber nun wollen wir uns dem eigentlichen Benchmark […]
[…] zweiten Grades in den Variablen . Es gibt daher strukturelle Ähnlichkeiten zu einigen der im zweiten Teil vorgestellten Testfunktionen, aber nun wollen wir uns dem eigentlichen Benchmark […]
[…] Erachtens nach – das wohl beliebteste Optimierungsverfahren im maschinellen Lernen, das Gradientenverfahren, hier keine guten Ergebnisse liefern, denn es gibt einfach zu viele lokale […]
[…] zweiten Grades in den Variablen . Es gibt daher strukturelle Ähnlichkeiten zu einigen der im zweiten Teil vorgestellten Testfunktionen, aber nun wollen wir uns dem eigentlichen Benchmark […]
Leave a Reply
Want to join the discussion?Feel free to contribute!