Die Clusteranalyse ist ein gruppenbildendes Verfahren, mit dem Objekte Gruppen – sogenannten Clustern zuordnet werden. Die dem Cluster zugeordneten Objekte sollen möglichst homogen sein, wohingegen die Objekte, die unterschiedlichen Clustern zugeordnet werden möglichst heterogen sein sollen. Dieses Verfahren wird z.B. im Marketing bei der Zielgruppensegmentierung, um Angebote entsprechend anzupassen oder im User Experience Bereich zur Identifikation sog. Personas.

Es gibt in der Praxis eine Vielzahl von Cluster-Verfahren, eine der bekanntesten und gebräuchlichsten Verfahren ist das K-Means Clustering, ein sog. Partitionierendes Clusterverfahren. Das Ziel dabei ist es, den Datensatz in K Cluster zu unterteilen. Dabei werden zunächst K beliebige Punkte als Anfangszentren (sog. Zentroiden) ausgewählt und jedem dieser Punkte der Punkt zugeordnet, zu dessen Zentrum er die geringste Distanz hat. K-Means ist ein „harter“ Clusteralgorithmus, d.h. jede Beobachtung wird genau einem Cluster zugeordnet. Zur Berechnung existieren verschiedene Distanzmaße. Das gebräuchlichste Distanzmaß ist die quadrierte euklidische Distanz:

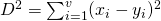
Nachdem jede Beobachtung einem Cluster zugeordnet wurde, wird das Clusterzentrum neu berechnet und die Punkte werden den neuen Clusterzentren erneut zugeordnet. Dieser Vorgang wird so lange durchgeführt bis die Clusterzentren stabil sind oder eine vorher bestimmte Anzahl an Iterationen durchlaufen sind.
Das komplette Vorgehen wird im Folgenden anhand eines künstlich erzeugten Testdatensatzes erläutert.

Zunächst wird ein Testdatensatz mit den Variablen „Alter“ und „Einkommen“ erzeugt, der 12 Fälle enthält. Als Schritt des „Data preprocessing“ müssen zunächst beide Variablen standardisiert werden, da ansonsten die Variable „Alter“ die Clusterbildung zu stark beeinflusst.

Das Ganze geplottet:

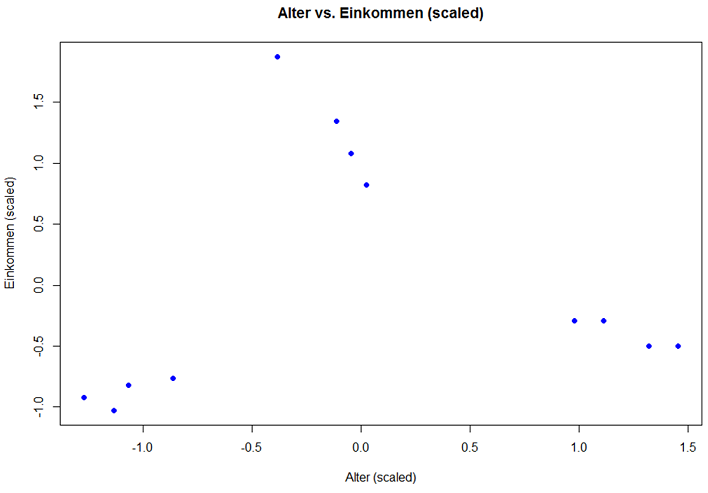
Wie bereits eingangs erwähnt müssen Cluster innerhalb möglichst homogen und zu Objekten anderer Cluster möglichst heterogen sein. Ein Maß für die Homogenität die „Within Cluster Sums of Squares“ (WSS), ein Maß für die Heterogenität „Between Cluster Sums of Squares“ (BSS).

Diese sind beispielsweise für eine 3-Cluster-Lösung wie folgt:

Sollte man die Anzahl der Cluster nicht bereits kennen oder sind diese extern nicht vorgegeben, dann bietet es sich an, anhand des Verhältnisses von WSS und BSS die „optimale“ Clusteranzahl zu berechnen. Dafür wird zunächst ein leerer Vektor initialisiert, dessen Werte nachfolgend über die Schleife mit dem Verhältnis von WSS und WSS gefüllt werden. Dies lässt sich anschließend per „Screeplot“ visualisieren.

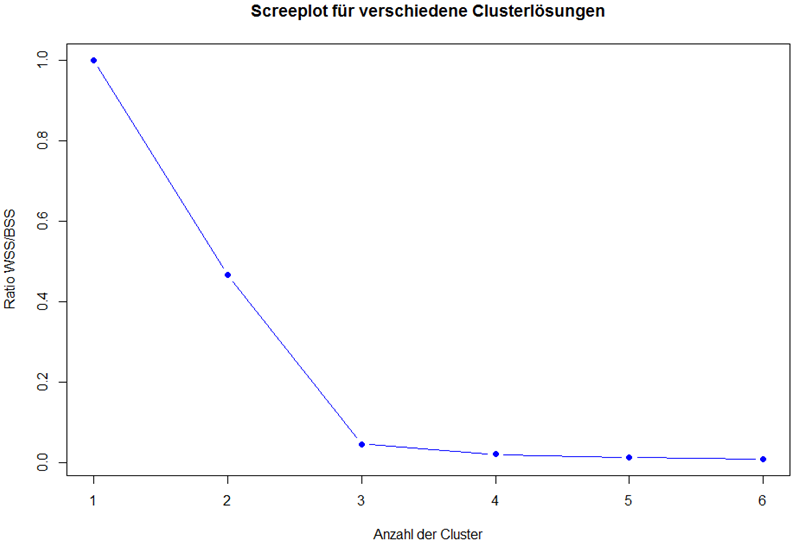
Die „optimale“ Anzahl der Cluster zählt sich am Knick der Linie ablesen (auch Ellbow-Kriterium genannt). Alternativ kann man sich an dem Richtwert von 0.2 orientieren. Unterschreitet das Verhältnis von WSS und BSS diesen Wert, so hat man die beste Lösung gefunden. In diesem Beispiel ist sehr deutlich, dass eine 3-Cluster-Lösung am besten ist.

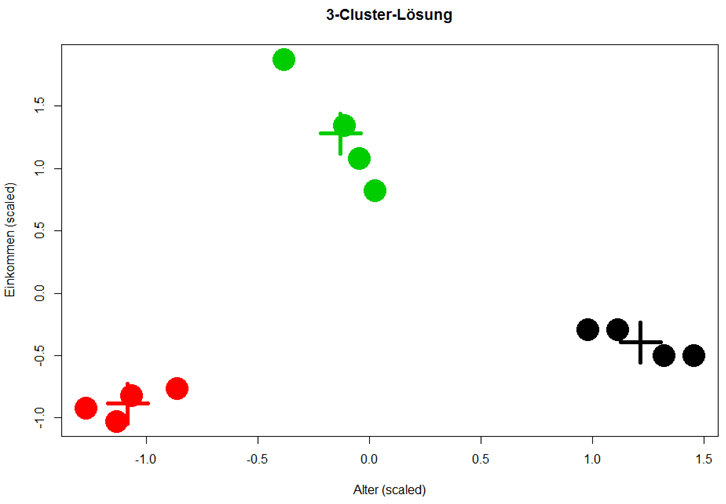
Fazit: Mit K-Means Clustering lassen sich schnell und einfach Muster in Datensätzen erkennen, die, gerade wenn mehr als zwei Variablen geclustert werden, sonst verborgen blieben. K-Means ist allerdings anfällig gegenüber Ausreißern, da Ausreißer gerne als separate Cluster betrachtet werden. Ebenfalls problematisch sind Cluster, deren Struktur nicht kugelförmig ist. Dies ist vor der Durchführung der Clusteranalyse mittels explorativer Datenanalyse zu überprüfen.