Fehler-Rückführung mit der Backpropagation

Dies ist Artikel 4 von 6 der Artikelserie –Einstieg in Deep Learning.

Das Gradienten(abstiegs)verfahren ist der Schlüssel zum Training einzelner Neuronen bzw. deren Gewichtungen zu den Neuronen der vorherigen Schicht. Wer dieses Prinzip verstanden hat, hat bereits die halbe Miete zum Verständnis des Trainings von künstlichen neuronalen Netzen.

Der Gradientenabstieg wird häufig fälschlicherweise mit der Backpropagation gleichgesetzt, jedoch ist das nicht ganz richtig, denn die Backpropagation ist mehr als die Anwendung des Gradientenabstiegs.

Bevor wir die Backpropagation erläutern, nochmal kurz zurück zur Forward-Propagation, die die eigentliche Prädiktion über ein künstliches neuronales Netz darstellt:

Forward-Propagation

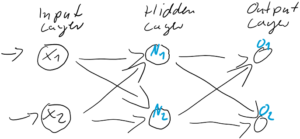
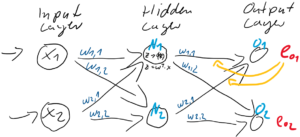
Abbildung 1: Ein simples kleines künstliches neuronales Netz mit zwei Schichten (+ Eingabeschicht) und zwei Neuronen pro Schicht.

In einem kleinen künstlichen neuronalen Netz, wie es in der Abbildung 1 dargestellt ist, und das alle Neuronen über die Sigmoid-Funktion aktiviert, wird jedes Neuron eine Nettoeingabe $z$ berechnen…

$z = w^{T} \cdot x$

… und diese Nettoeingabe in die Sigmoid-Funktion einspeisen…

$\phi(z) = sigmoid(z) = \frac{1}{1 + e^{-z}}$

… die dann das einzelne Neuron aktiviert. Die Aktivierung erfolgt also in der mittleren Schicht (N-Schicht) wie folgt:

$N_{j} = \frac{1}{1 + e^{- \sum (w_{ij} \cdot x_{i}) }}$

Die beiden Aktivierungsausgaben $N$ werden dann als Berechnungsgrundlage für die Ausgaben der Ausgabeschicht $o$ verwendet. Auch die Ausgabe-Neuronen berechnen ihre jeweilige Nettoeingabe $z$ und aktivieren über Sigmoid( $z$ ).

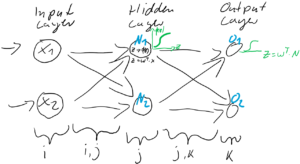
Ausgabe eines Ausgabeknotens als Funktion der Eingänge und der Verknüpfungsgewichte für ein dreischichtiges neuronales Netz, mit nur zwei Knoten je Schicht, kann also wie folgt zusammen gefasst werden:

$O_{k} = \frac{1}{1 + e^{- \sum (w_{jk} \cdot \frac{1}{1 + e^{- \sum (w_{ij} \cdot x_{i}) }}) }}$

Abbildung 2: Forward-Propagation. Aktivierung via Sigmoid-Funktion.

Sollte dies die erste Forward-Propagation gewesen sein, wird der Output noch nicht auf den Input abgestimmt sein. Diese Abstimmung erfolgt in Form der Gewichtsanpassung im Training des neuronalen Netzes, über die zuvor erwähnte Gradientenmethode. Die Gradientenmethode ist jedoch von einem Fehler abhängig. Diesen Fehler zu bestimmen und durch das Netz zurück zu führen, das ist die Backpropagation.

Back-Propagation

Um die Gewichte entgegen des Fehlers anpassen zu können, benötigen wir einen möglichst exakten Fehler als Eingabe. Der Fehler berechnet sich an der Ausgabeschicht über eine Fehlerfunktion (Loss Function), beispielsweise über den MSE (Mean Squared Error) oder über die sogenannte Kreuzentropie (Cross Entropy). Lassen wir es in diesem Beispiel einfach bei einem simplen Vergleich zwischen dem realen Wert (Sollwert $o_{real}$ ) und der Prädiktion (Ausgabe $o$ ) bleiben:

$e_{o} = o_{real} - o$

Der Fehler $e$ ist also einfach der Unterschied zwischen dem Ziel-Wert und der Prädiktion. Jedes Training ist eine Wiederholung von Prädiktion (Forward) und Gewichtsanpassung (Back). Im ersten Schritt werden üblicherweise die Gewichtungen zufällig gesetzt, jede Gewichtung unterschiedlich nach Zufallszahl. So ist die Wahrscheinlichkeit, gleich zu Beginn die “richtigen” Gewichtungen gefunden zu haben auch bei kleinen neuronalen Netzen verschwindend gering. Der Fehler wird also groß sein und kann über den Gradientenabstieg durch Gewichtsanpassung verkleinert werden.

In diesem Beispiel berechnen wir die Fehler $e_{1}$ und $e_{2}$ und passen danach die Gewichte $w_{j,k}$ ( $w_{1,1}$ & $w_{2,1}$ und $w_{1,2}$ & $w_{2,2}$ ) der Schicht zwischen dem Hidden-Layer $N$ und dem Output-Layer $o$ an.

Abbildung 3: Anpassung der Gewichtungen basierend auf dem Fehler in der Ausgabe-Schicht.

Die Frage ist nun, wie die Gewichte zwischen dem Input-Layer $X$ und dem Hidden-Layer $N$ anzupassen sind. Es stellt sich die Frage, welchen Einfluss diese auf die Fehler in der Ausgabe-Schicht haben?

Um diese Gewichtungen anpassen zu können, benötigen wir den Fehler-Anteil der beiden Neuronen $N_{1}$ und $N_{2}$ . Dieser Anteil am Fehler der jeweiligen Neuronen ergibt sich direkt aus den Gewichtungen $w_{j,k}$ zum Output-Layer:

$e_{N_{1}} = e_{o1} \cdot \frac{w_{1,1}}{w_{1,1} + w_{1,2}} + e_{o2} \cdot \frac{w_{1,2}}{w_{1,1} + w_{1,2}}$

$e_{N_{2}} = e_{o1} \cdot \frac{w_{2,1}}{w_{2,1} + w_{2,2}} + e_{o2} \cdot \frac{w_{2,2}}{w_{2,1} + w_{2,2}}$

Wenn man das nun generalisiert:

$e_{N} = \left(\begin{array}{rr} \frac{w_{1,1}}{w_{1,1} + w_{1,2}} & \frac{w_{1,2}}{w_{1,1} + w_{1,2}} \\ \frac{w_{2,1}}{w_{2,1} + w_{2,2}} & \frac{w_{2,2}}{w_{2,1} + w_{2,2}} \end{array}\right) \cdot \left(\begin{array}{c} e_{1} \\ e_{2} \end{array}\right) \qquad$

Dabei ist es recht aufwändig, die Gewichtungen stets ins Verhältnis zu setzen. Diese Berechnung können wir verkürzen, indem ganz einfach direkt nur die Gewichtungen ohne Relativierung zur Kalkulation des Fehleranteils benutzt werden. Die Relationen bleiben dabei erhalten!

$e_{N} = \left(\begin{array}{rr} w_{1,1} & w_{1,2} \\ w_{2,1} & w_{2,2} \end{array}\right) \cdot \left(\begin{array}{c} e_{1} \\ e_{2} \end{array}\right) \qquad$

Oder folglich in Kurzform: $e_{N} = w^{T} \cdot e_{o}$

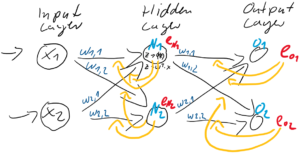
Abbildung 4: Vollständige Gewichtsanpassung auf Basis der Fehler in der Ausgabeschicht und der Fehleranteile in der verborgenden Schicht.

Und nun können, basierend auf den Fehleranteilen der verborgenden Schicht $N$ , die Gewichtungen $w_{i,j}$ zwischen der Eingabe-Schicht $I$ und der verborgenden Schicht $N$ angepasst werden, entgegen dieser Fehler $e_{N}$ .

Die Backpropagation besteht demnach aus zwei Schritten:

Fehler-Berechnung durch Abgleich der Soll-Werte mit den Prädiktionen in der Ausgabeschicht und durch Fehler-Rückführung zu den Neuronen der verborgenden Schichten (Hidden-Layer)
Anpassung der Gewichte entgegen des Gradientenanstiegs der Fehlerfunktion (Loss Function)

Buchempfehlungen

Die folgenden zwei Bücher haben mir sehr beim Verständnis und beim Verständlichmachen der Backpropagation in künstlichen neuronalen Netzen geholfen.


Neuronale Netze selbst programmieren: Ein verständlicher Einstieg mit Python	Deep Learning. Das umfassende Handbuch: Grundlagen, aktuelle Verfahren und Algorithmen, neue Forschungsansätze (mitp Professional)

About Author

Benjamin Aunkofer

Benjamin Aunkofer ist Gründer von DATANOMIQ und Hochschul-Dozent für Data Science und Data Strategy. Darüber hinaus arbeitet er als Interim Head of Business Intelligence und gibt Seminare/Workshops zu den Themen BI, Data Science und Machine Learning für Unternehmen.

See author's posts

ProTom says:

June 4, 2020 at 12:42 pm

Hallo, ich bin Anfänger in Sachen neuronale Netzwerke. Ich hätte da eine grundsätzliche Frage zum Thema Fehlerberechung und entsprechender Modifikation der Stärke des jeweiligen Gewichtes. Dies wird ja auch in diesem Blog erklärt. Warum muss man sich eigentlich den Fehler berechnen und schrittweise an die richtige Gewichtsstärke annähern? Man könnte doch die richtige Stärke des Gewichtes viel einfacher berechnen mittels einer simplen Quotientenbildung wie beim Dreisatz, d.h. bei Abweichung der Ladung des Neurons von einem gewünschten Zielwert die Stärke des Gewichtes analog erhöhen oder erniedrigen, z.B. Gewicht(aktuell)/Gewicht(gewünscht) = LadungNeuron(aktuell)/LadungNeuron(gewünscht) => Gewicht(gewünscht) = Gewicht(aktuell) * (Ladung(gewünscht)/Ladung(aktuell)). Warum muss man sich umständlich mittels z.B. einer Quadrat-Fehlerfunktion schrittweise annähern? Offensichtlich hab ich da einen Denkfehler, oder hängt es damit zusammen, daß ja mehrere Muster gelernt werden müssen und daher die von mir vorgeschlagene Berechnung die anderen Muster bzw. erlernten Gewichte löschen würde? Vielen Dank im voraus für eine Erklärung! T.P.

Thor says:

December 29, 2022 at 11:14 am

Eine gute Erklärung arbeitet stets mit einer Beispielrechnung und Zahlen zur Verdeutlichung, damit sich die Formeln leichter interpretieren lassen. Weil das so gut wie niemand macht, darf man sich unzählige Texte anschauen, um es schlussendlich immer noch nicht zu verstehen. Zahlen würden auch dazu beitragen, dass mit den Gradienten, der Fehlerberechnung und der back propagation zu verstehen. Weniger aufgeblähter Formelsalat würde auch etwas mehr Licht ins Dunkel bringen.