o. Installation von TensorFlow
Bevor wir richtig durchstarten können, müssen wir natürlich TensorFlow erstmal installieren. Auf dieser Seite findet ihr eine ausführliche Anleitung, wie man TensorFlow auf allen möglichen Systemen installiert. Die nächsten Schritte beschränken sich auf die Installation auf Windows.
o.1. Installation mit pip
Um TensorFlow zu nutzen, müssen wir diesen Framework auch erstmal installieren. Am einfachsten ist die Installation, wenn ihr Python in reiner Form auf euren Rechner habt. Dann ist es vollkommen ausreichend, wenn ihr folgenden Befehl in eure Eingabeaufforderung(Windows: cmd) eingebt:
|
|
pip3 install --upgrade tensorflow |
Stellt bei dieser Installation sicher, dass ihr keine ältere Version von Python habt als 3.5.x. Außerdem ist es erforderlich, dass ihr pip installiert habt und Python bei euch in der PATH-Umgebung eingetragen ist.Besitzt ihr eine NVIDIA® Grafikkarte so könnt ihr TensorFlow mit GPU Support nutzen. Dazu gebt ihr statt des oben gezeigten Befehls folgendes ein:
|
|
pip3 install --upgrade tensorflow gpu |
o.2. Installation mit Anaconda
Ein wenig aufwendiger wird es, wenn ihr die beliebte Anaconda Distribution nutzt, weil wir da eine Anaconda Umgebung einrichten müssen. Auch hier müssen wir wieder in den Terminal bzw. in die Eingabeaufforderung und folgenden Befehl eingeben:
|
|
conda create -n tensorflow pip python=3.x |
Tauscht das x mit eurer genutzten Version aus.(x = 5, 6) Danach aktiviert ihr die erstellte Umgebung:
Nun installieren wir TensorFlow in unsere erstellte Umgebung. Ohne GPU Support
|
|
pip install --ignore-installed --upgrade tensorflow |
mit GPU Support
|
|
pip install --ignore-installed --upgrade tensorflow-gpu |
Es sei erwähnt, dass das Conda package nur von der Community unterstützt wird, jedoch nicht offiziell seitens Google.
o.3. Validierung der Installation
Der einfachste Weg um zu überprüfen ob unsere Installation gefruchtet hat und funktioniert können wir anhand eines einfachen Beispiels testen. Dazu gehen wir wieder in den/die Terminal/Eingabeaufforderung und rufen python auf, indem wir python eingeben.
|
|
import tensorflow as tf hello = tf.constant('Hello, TensorFlow!') sess = tf.Session() print(sess.run(hello)) |
1. Grundverständnis für TensorFlow
1.1. Datenstrom-orientierte Programmierung
In diesem Artikel wollen wir näher auf die Funktionsweise von TensorFlow eingehen. Wie wir aus dem ersten Artikel dieser Serie wissen, nutzt TensorFlow das datenstrom-orientierte Paradigma. In diesem wird ein Datenfluss-Berechnungsgraph erstellt, welcher aus Knoten und Kanten besteht. Ein Datenfluss-Berechnungsgraph, Datenflussgraph oder auch Berechnungsgraph kann mehrere Knoten haben, die wiederum durch die Kanten verbunden sind. In TensorFlow steht jeder Knoten für eine Operation, die Auswirkungen auf eingehende Daten haben.
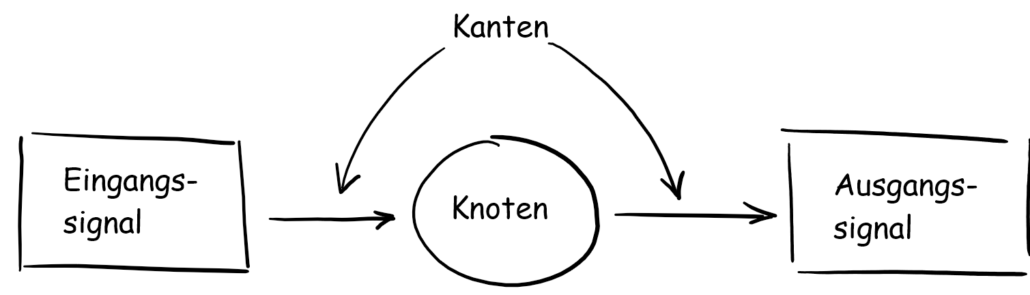
Abb.1: Knoten und Kanten: Das Eingangssignal wird durch Kanten in den Knoten eingespeist, verändert und ausgegeben

Abb. 1.5: Achterbahn mit fehlender Verbindung [Quelle]
Analogie-Beispiel: Stellt euch vor ihr seid in einem Freizeitpark und habt Lust eine Achterbahn zu fahren. Am Anfang seid ihr vielleicht ein wenig nervös, aber euch geht es noch sehr gut. Wie jeder von euch weiß, hat eine Achterbahn verschiedene Fahrelemente eingebaut, die unsere Emotionen triggern und bei manchen vielleicht sogar auf den Magen schlagen. Diese Elemente sind äquivalent unsere Knoten. Natürlich müssen diese Elemente auch verbunden sein, sonst wäre eine Fahrt mit dieser Achterbahn in meinen Augen nicht empfehlenswert. Diese Verbindungsstücke sind unsere Kanten und somit sind wir die Daten/Signale, die von Knoten zu Knoten durch die Kanten weitergeleitet werden. Schauen wir uns Abb. 2 an, in der eine schematische Darstellung einer fiktiven Achterbahn zu sehen ist, welche mit 4 Fahrelementen dienen kann.
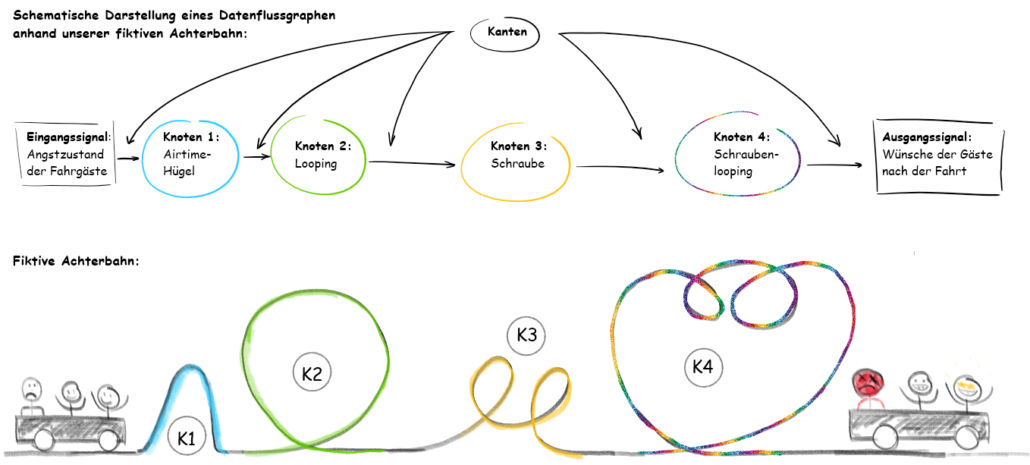
Abb. 2: Oben: Schematische Darstellung eines Datenflussgraphen anhand unserer fiktiven Achterbahn Unten: Unsere fiktive Achterbahn
- Airtime-Hügel: Ein Airtime-Hügel erzeugt bei der Überfahrt Schwerelosigkeit und in manchen Fällen ein Abheben aus dem Sitz. Ein guter Einstieg für die Mitfahrer, wie ich finde.
- Klassischer Looping: Wir kennen ihn alle, den Looping. Mit hoher Geschwindigkeit geht es in einen vertikalen Kreis hinein und man sich am höchsten Punkt kopfüber befindet. Für Leute mit nicht so starken Nerven fragen sich spätestens jetzt, warum sie überhaupt mitgefahren sind.
- Korkenzieher/Schraube: Der Korkenzieher kann als auseinander gezogener Looping beschrieben werden.
- Schraubel-Looping : Und zu guter Letzt kombinieren wir einen Looping mit einer Schraube! Ein Teil unserer Mitfahrer sucht den nächsten Busch auf, ein anderer Teil will am liebsten nochmal fahren und der Rest wird jetzt einen Pause brauchen.
Fakt ist, dass die Fahrelemente/Knoten unsere anfänglichen Emotionen/Eingangsdatensignale geändert haben.
1.2. Genereller Ablauf in TensorFlow
Anhand unser fiktiven Achterbahn haben wir das Prinzip der datenstrom-orientierten Programmierung eingefangen. Damit wir aber erst einmal Achterbahn fahren können, müssen wir diese konstruieren. Das gilt auch in TensorFlow und können die Arbeit in zwei wesentliche Phasen unterteilen:
- Erstellen eines Berechnungsgraphen: Wie auch bei einer Achterbahn müssen wir unser Modell erst einmal modellieren. Je nachdem welche Ressourcen uns zur Verfügung gestellt werden, welche Bedingungen wir folgen müssen, können wir unser Modell darauf aufbauen und gestalten.
- Ausführung des Berechnungsgraphen: Nachdem wir das Modell/den Graph fertig konstruiert haben, führen wir diese nun aus, d.h. für unsere Achterbahn, dass wir den Strom anschalten und losfahren können.
2. Erstellung eines Graphen
2.1. TensorFlow-Operatoren
Wie bereits erwähnt können Knoten verschiedene Operationen in sich tragen. Das können z.B. Addition, Substraktion oder aber auch mathematische Hyperbelfunktionen à la Tangens Hyperbolicus Operatoren sein. Damit TensorFlow mit den Operatoren arbeiten kann, müssen wir diese mit den zur Verfügung gestellten Operatoren von TensorFlow auskommen. Eine vollständige Dokumentation findet ihr hier.
2.2. Platzhalter
Wenn in TensorFlow Daten aus externen Quellen in den Berechnungsgraph integriert werden sollen, dann wird eine eigens dafür entwickelte Struktur genutzt um die Daten einzulesen; dem Platzhalter. Ihr könnt euch den Platzhalter als Wagon unserer Achterbahn vorstellen, der die Mitfahrer (Daten bzw. Tensoren) durch die Achterbahn (Berechnungsgraph) jagt.
Es ist bei der Modellierung eines Berechnungsgraphen nicht notwendig, die Daten am Anfang einzuspeisen. Wie der Name schon sagt, setzt TensorFlow eine ‘leere Größe’ ein, die in der zweiten Phase gefüllt wird.
Eine Frage, die ich mir damals gestellt habe war, warum man einen Platzhalter braucht? Dazu können wir uns wieder unsere Achterbahn nehmen. Bei 2-3 Fahrgästen besteht kein Problem; wir hätten genug Platz/Ressourcen um diese unterzubringen. Aber was machen wir, wenn wir 10.000 Gäste haben, wie es auch in der Realität ist ? Das ist auch bei neuronalen Netzen der Fall, wenn wir zu viele Daten haben, dann stoßen wir irgendwann an unser Leistungslimit. Wir teilen unsere Daten/Gäste so auf, dass wir damit arbeiten können.
2.3. Variable
Stellen wir uns folgendes Szenario vor: Wir haben eine Achterbahn fertig konstruiert – wahrscheinlich die beste und verrückteste Achterbahn, die es jemals gegeben hat. Je nachdem welchen Effekt wir mit unserer Achterbahn erzielen wollen; z.B. ein einfacher Adrenalinschub, ein flaues Gefühl im Magen oder den vollständigen Verlust jeglicher Emotionen aus purer Angst um das eigene Leben, reicht es nicht nur ein schönes Modell zu bauen. Wir müssen zusätzlich verschiedene Größen anpassen um das Erlebnis zu maximieren. Eine wichtige Größe für unsere Achterbahn wäre die Geschwindigkeit (in neuronalen Netzen sind es die Gewichte), die über den Fahrspaß entscheidet. Um die optimale Geschwindigkeit zu ermitteln, müssen viele Versuche gemacht werden (sei es in der Realität oder in der Simulation) und nach jedem Test wird die Geschwindigkeit nach jedem Test angepasst. Zu diesem Zweck sind die Variablen da. Sie passen sich nach jedem Versuch an.
2.4. Optimierung
Damit die Variablen angepasst werden können, müssen wir TensorFlow Anweisungen geben, wie er die Variablen optimiert werden soll. Dafür müssen wir eine Formel an TensoFlow übermitteln, die dann optimiert wird. Auch hat man die Auswahl von verschiedenen Optimierer, die die Aufgabe anders optimieren. Die Wahl der richtigen Formel und des passenden Optimierer ist jedoch eine Sache, die ohne weiteres nicht zu beantworten ist. Wir wollen ein anderes Mal Bezug auf diese Frage nehmen.
3. Ausführung eines Graphen
Wie die Ausführung des Graphen von statten läuft, schauen wir uns im nächsten Abschnitt genauer an. Es sei so viel gesagt, dass um eine Ausführung einzuleiten wir den Befehl tf.Session() benötigen. Die Session wird mit tf.Session().run()gestartet und am Ende mit tf.Session().close() geschlossen. In der Methode .run()müssen die ausgeführten Größen stehen und außerdem der Befehl feed_dict= zum Befüllen der Platzhalter.
4. Beispiel: Achterbahn des Grauens – Nichts für schwache Nerven
4.1 Erklärung des Beispiels
Wir haben jetzt von so vielen Analogien gesprochen, dass es alles ein wenig verwirrend sein kann. Daher nochmal eine Übersicht zu den wesentlichen Punkten:
| TensorFlow |
Neuronales Netz |
Achterbahn |
| Knoten |
Neuron |
Fahrelement |
| Variable |
Gewichte, Bias |
Geschwindigkeit |
| Kanten |
Signale |
Zustand der Fahrer |
| Platzhalter |
|
Wagon |
Tab.1: Analogie unser fiktiven Achterbahn
Nun haben wir so viel Theorie gehört, jetzt müssen auch Taten folgen! Weshalb wir unsere Achterbahn modellieren wollen. Zu unserem Beispiel: Wir wollen eine Achterbahn bauen, welche ängstlichen Mitfahrer noch ängstlicher machen soll und diese sollen am Ende der Fahrt sich wünschen nie mitgefahren zu sein. (Es wird natürlich eine stark vereinfachte Variante werden, die aber auf all unsere Punkte eingehen soll, die wir im oberen Teil angesprochen haben.)
Wie im bereits beschrieben, unterteilt sich die Arbeit in TensorFlow in zwei Phasen:
- Erstellung des Graphen: In unserem Falle wäre das die Konstruktion unserer Achterbahn.
- Ausführung des Graphen: In dieser Phase lassen wir unsere Insassen einfach los und schauen mal was passiert.
Um die Zahlen zu verstehen, möchte ich euch zudem erklären, was überhaupt das Ziel unseres Modells ist. Wir haben 8 Probanden mit verschiedenen Angstzuständen. Der Angstzustand ist in unserem Beispiel ein quantitativer Wert, Menge der ganzen Zahlen und je größer dieser Wert ist, desto ängstlicher sind unsere Probanden. Unser Ziel ist es alle Probanden in Angst und Schrecken zu versetzen, die einen Angstzustand >5 haben und sich nach der Fahrt wünschen unserer Achterbahn nie mitgefahren zu sein! Die Größe die wir dabei optimieren wollen, ist die Geschwindigkeit. Wenn die Geschwindigkeit zu schnell ist, dann fürchten sich zu viele, wenn wir zu langsam fahren, dann fürchtet sich womöglich niemand. Außerdem benötigen wir noch eine Starthöhe, die wir dem Modell zugeben müssen.
Wir haben somit eine Klassifikationsaufgabe mit dem Ziel die Geschwindigkeit und die Starthöhe zu optimieren, damit sich Fahrgäste mit einem Angstzustand > 5 so eine schlechte Erfahrung machen, dass sie am liebsten nie mitgefahren wären.
Wir benötigen außerdem für unser Beispiel folgende Module:
|
|
import tensorflow as tf import matplotlib.pyplot as plt import numpy as np |
4.2. Eingangssignale: Zustände der Gäste
Wir sehen hier zwei Vektoren bzw. Tensoren die Informationen über unsere Gäste haben.
x_input ist der Angstzustand unserer Gästey_input ist unser gewünschtes Ausgangsssignal: 0 → normal, 1 → Wunsch nicht mitgefahren zu sein
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
# Eingangssignale, Tensor # Zustand der Gäste -> je größer die Zahl desto größer der Angstzustand der Gäste x_input = [[-10], # <- Angstzustand Gast 1 [-5], # <- Angstzustand Gast 2 [-2], # <- Angstzustand Gast 3 [-1], # . [2], # . [1], # . [6], # . [9]] # <- Angstzustand Gast 8 # gewünschtes Ausgangssignal, Tensor # Endzustand der Gäste -> Wunsch die Bahn nie gefahren zu sein y_input = [[0], [0], [0], [0], [0], [0], [1], # <- bereut die Fahrt [1]] # <- bereut die Fahrt |
4.3. Erstellung unseres Graphen: Konstruktion der Achterbahn
Nun konstruieren wir unsere Achterbahn des Grauens:
Eine Gleichrichter-Aktivierungsfunktion (engl. rectifier) mit einer Matrizenmultiplikation aus einem Vektor und einem Skalar mit anschließender Fehleroptimierung! MuhahahahaHAHAHAHA!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
# Platzhalter # Wagon, Eingangsgröße wag = tf.placeholder(tf.float32, shape = [8, 1]) # gewünschter Endzustand der Gäste y_true = tf.placeholder(tf.float32, shape = [8, 1]) # Variable # Geschwindigkeit des Wagons v = tf.Variable([[1.0,]]) # Starthöhe des Wagons h = tf.Variable([[-2.0]]) # Knoten mit Matrizenoperator, Fahrelement, z.B. Airtime-Hügel z = tf.matmul(wag, v) + h # Knoten mit ReLu-Aktivierungsfunktion y_pred = tf.nn.relu(z) # Fehlerfunktion err = tf.square(y_true - y_pred) # Optimierer opt = tf.train.AdamOptimizer(learning_rate=0.01).minimize(err) # Initialisierung der Variablen (Geschwindigkeit) init = tf.global_variables_initializer() |
Auf den ersten Blick vielleicht ein wenig verwirrend, weshalb wir alles Schritt für Schritt durchgehen:
wag = tf.placeholder(tf.float32, shape = [8, 1]) ist unser Wagon, welcher die Achterbahn auf und ab fährt. Gefüllt mit unseren Probanden. Die Daten der Probanden (x_input)sind externe Daten und damit geeignet für einen Platzhalter.
- Wichtig bei Platzhalter ist, dass ihr den Datentyp angeben müsst!
- Optional könnt ihr auch die Form angeben. Bei einem so überschaubaren Beispiel machen wir das auch. (Form unseres Vektors: 8×1)
y_true = tf.placeholder(tf.float32, shape = [8, 1]) ist der gewünschte Endzustand unserer Gäste, den wir uns für die Probanden erhoffen, d.h. es ist unser y_input. Auch hier kommen die Daten von außerhalb und daher wird der Platzhalter genutzt.v, h sind Geschwindigkeit und Starthöhe, die optimiert werden müssen; perfekt für eine Variable!
- Variablen brauchen am Anfang immer einen Initialisierungswert. Für
v soll es 1 sein und für h soll es -2 sein. Außerdem liegen diese Größen als Skalare (1×1) vor.
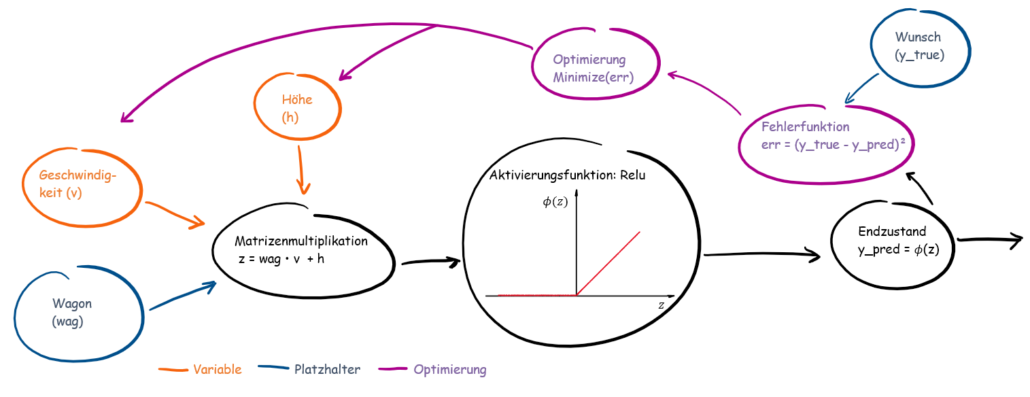
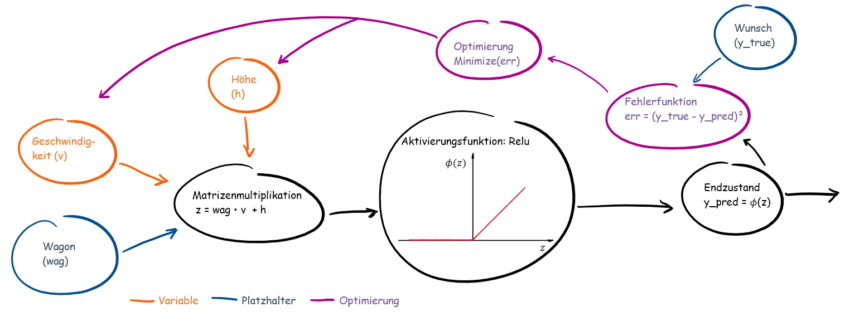
Abb.2: Schematische Darstellung unseres Berechnungsgraphen
Nun zum zweiten Teil der Modellierung in dem wir ein klein wenig Mathematik benötigen. Schauen wir uns folgende Gleichung an:
z = tf.matmul(wag, v) + h: ist unsere Matrizenmultiplikation -> Da unsere Größen in Vektoren/Tensoren vorliegen, können wir diese nicht einfach multiplizieren, wie z.B. 2*2 = 4. Bei der Multiplikation von Matrizen oder Vektoren müssen bestimmte Bedingungen herrschen, damit diese überhaupt multipliziert werden können. Eine ausführlichere Erklärungen soll demnächst folgen.y_pred = tf.nn.relu(z): Für all diejenigen, die sich bereits mit neuronalen Netzen beschäftigt haben; relu ist in unserem Fall die Aktivierungsfunktion. Für alle anderen, die mit der Aktivierungsfunktion noch nichts anfangen können: Die Kombination (Matrizenmultiplikation) aus dem Angstzustand und der Geschwindigkeit ist der Wert Z. Je nachdem welche Aktivierungsfunktion genutzt wird, triggert der Wert Z unsere Emotionen, so dass wir den Wunsch verspüren, die Bahn nie gefahren zu sein.err = tf.square(y_true - y_pred):Quadriert die Differenz der tatsächlichen und der ermittelten Werte. -> die zu optimierende Funktionopt = tf.train.AdamOptimizer(learning_rate=0.01).minimize(err)Unser gewählter Optimierer mit der Lernrate 0.01.init = tf.global_variables_initializer() Initialisierung der Variablen
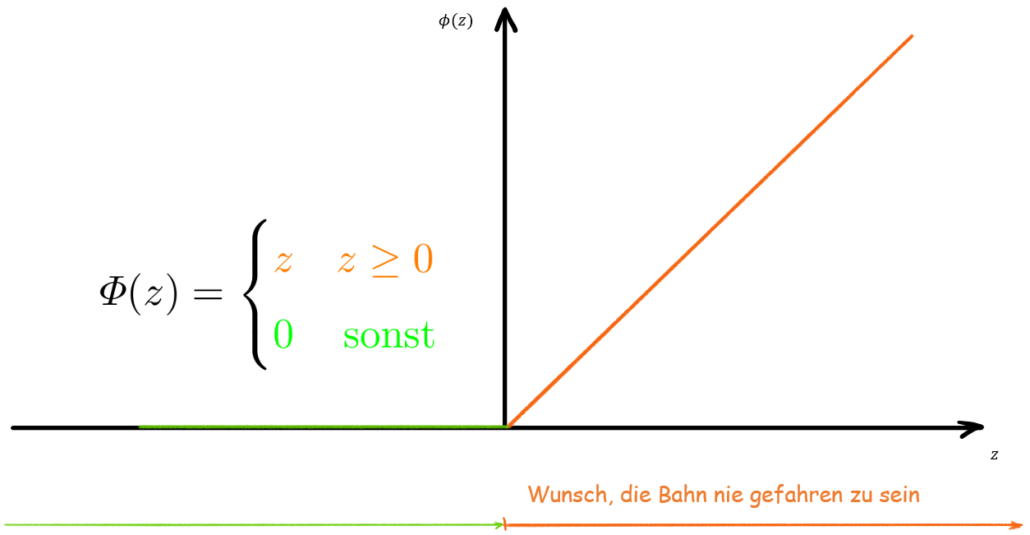
Abb. 3: Aktivierungsfunktion ReLu
4.4. Ausführung des Graphen: Test der Achterbahn
Wenn wir den unten stehenden Code mal grob betrachten, dann fällt vor allem die Zeile mit dem with-(Python)Operator und dem tf.Session()-(TensorFlow)Operator auf. Der tf.Session()-Operator leitet unsere Ausführung ein. Warum wir with nutzen hat den Grund, dass dieser Operator uns das Leben einfacher macht, da dieser die nachfolgenden Befehle wieder schließt und damit wieder Leistungsressourcen frei werden. Werden zum Beispiel Daten aus externen Quellen benötigt – sei es eine Excel- oder eine SQL-Tabelle – dann schließt uns der with Operator die geöffneten Dateien, nachdem er alle unsere Befehle durchgeführt hat.
Durch die Methode .run() werden dann die in der Klammer befindenden Größen bearbeitet. Mit dem Parameter feed_dict= füllen wir den Graphen mit unseren gewünschten Dateien.
Wir lassen das Ganze 100 mal Testfahren um die optimalen Variablen zu finden. In Abb. 4 sehen wir die Verläufe der Fehlerfunktion, der Geschwindigkeit und der Höhe.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
# Rundenanzahl runden = 100 # Array zum notieren der Größen v_array = [] h_array = [] # Aufzeichnung des Fehlerwertes loss = [] # Ausführung des Graphen with tf.Session() as sess: # Initialisierung dar Variablen sess.run(init) # Beginn der 100 Fahrten for i in range(runden): # Ausgabe der Werte _, geschw ,hoehe ,Y_pred , error = sess.run([opt,v,h , y_pred, err], feed_dict = {wag:x_input, y_true:y_input } ) loss.append(np.mean(error)) v_array.append(float(geschw)) h_array.append(float(hoehe)) # Ausgabe der letzten Werte print('Angstlvl: \n {}'.format(Y_pred)) print('\n Geschwindigkeit: {}'.format(geschw)) print('\n Starthöhe: {}'.format(hoehe)) print('\n Fehler: {}'.format(error)) |
In Tab.2 sind nun zwei Fahrgäste zu sehen, die sich wünschen, die Bahn nie gefahren zu sein! Deren Angstlevel () ist über 0 und damit wird der Wunsch getriggert wurde; so wie wir es auch beabsichtigt haben!
| Angstlvl berechnet: |
Fehler: |
Geschwindigkeit: |
Starthöhe: |
| [0. ] |
[0. ] |
[0.4536] |
[-2.5187] |
| [0. ] |
[0. ] |
|
|
| [0. ] |
[0. ] |
|
|
| [0. ] |
[0. ] |
|
|
| [0. ] |
[0. ] |
|
|
| [0. ] |
[0. ] |
|
|
| [0.2060 ] -> Wunsch getriggert |
[0.6304] |
|
|
| [1.5685] -> Wunsch getriggert |
[0.3231] |
|
|
Tab.2: Endergebnisse der letzten Runde
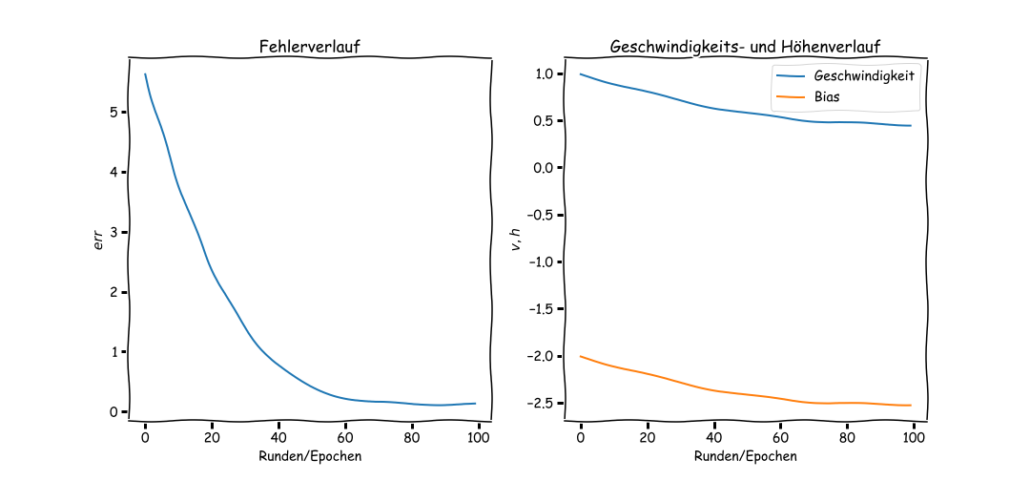
Abb.4: Verläufe der Fehler-, Geschwindigkeits- und Höhenfunktion durch Optimierung
5. Zusammenfassung und Ausblick
Zugegeben ist dieser ganze Aufwand für ein mehr oder weniger linearen Zusammenhang etwas übertrieben und bestimmt ist dem einen oder anderen aufgefallen, dass unser Beispiel mit der Achterbahn an manchen Stellen hinkt. Dennoch hoffe ich, dass ich mit der Analogie das Verständnis von TensorFlow rüberbringen konnte. Lasst uns daher nochmal die wichtigsten Punkte zusammenfassen:
Die Arbeit mit TensorFlow unterteilt sich in folgende Phasen:
- Erstellung des Graphen: In dieser Phase konzentrieren wir uns darauf einen Berechnungsgraphen zu erstellen, welcher so konzipiert wird, dass er uns am Ende das Ergebnis ausgibt, welches wir uns wünschen.
- Platzhalter: Eine der wichtigsten Sturkturen in TensorFlow ist der Platzhalter. Er ist dafür zuständig, wenn es darum geht externe Daten in unseren Graph einfließen zu lassen. Bei der Erstellung eines Platzhalters müssen wir zumindest den Datentypen angeben.
- Variable: Wenn es darum geht Größen für ein Modell zu optimieren, stellt TensorFlow Variablen zur Verfügung. Diese benötigen eine Angabe, wie die Form des Tensors aussehen soll.
- Ausführung des Graphen: Nachdem wir unseren Graphen entwickelt haben, ist der nächste Schritt diesen auszuführen.
- Dies machen wir mit dem Befehl
tf.Session() und führen diesen dann mit der Methode .run() aus
- Ebenfalls hat die Optimierung einen wichtigen Bestand in dieser Phase
- Um unseren Graphen mit den Daten zu füllen, nutzen wir den wird den Parameter
feed_dict=
Um diesen Artikel nicht in die Länge zu ziehen, wurden die Themen der Matrizenmultiplikation, Aktivierungsfunktion und Optimierung erstmal nur angerissen. Wir wollen in einem separaten Artikel näher darauf eingehen. Für den Anfang genügen wir uns damit, dass wir von diesen Elementen wissen und dass sie einen wichtigen Bestandteil haben, wenn wir neuronale Netze aufbauen wollen.
In nächsten Artikel werden wir dann ein Perzeptron erstellen und gehen auch näher auf die Themen ein, die wir in diesem Teil nur angerissen haben. Bleibt gespannt!
6. Bonus-Material
Mit Tensorboard ist es möglich unseren entwickelten Graphen auch plotten und auszugeben zu lassen. So sieht unser Graph aus:
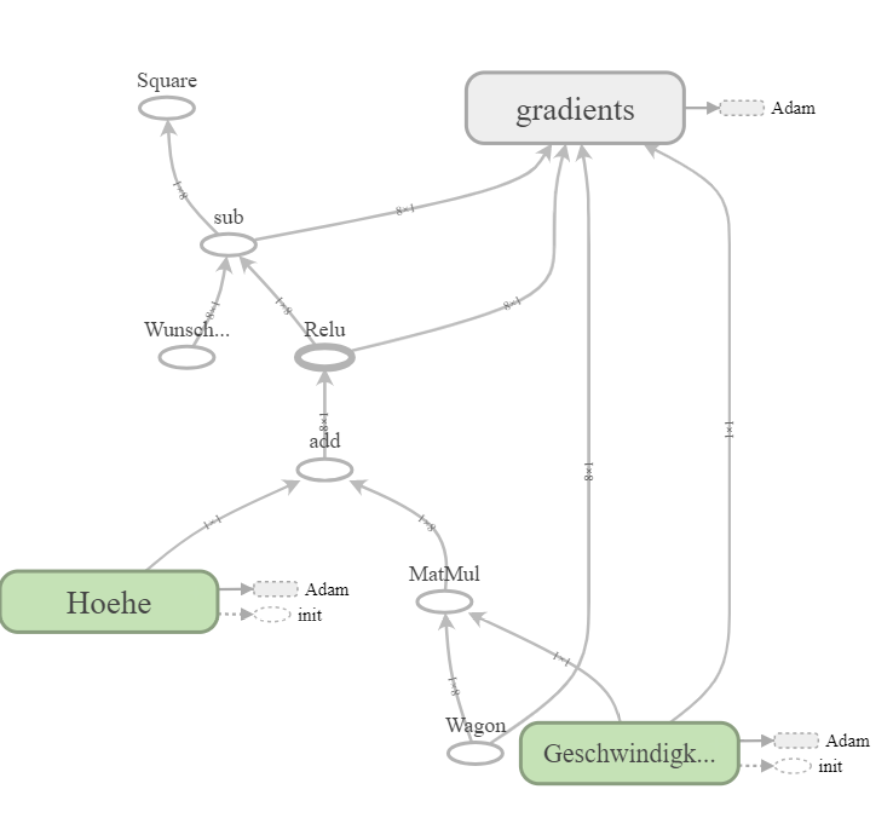
Abb.5.: Tensorboard Berechnungsgraphausgabe
Den Programmiercode könnt ihr in diesem Link auch als Ganzes betrachten.