Kiano – visuelle Exploration mit Deep Learning
Kiano – eine iOS-App zur visuellen Exploration und Suche der eigenen Fotos.
Menschen haben kein Problem, komplexe Bilder zu verstehen, es fällt ihnen aber schwer, gezielt Bilder in großen Bildersammlungen (wieder) zu finden. Da die Anzahl von Bildern, insbesondere auch auf Smartphones zusehends zunimmt – mehrere tausend Bilder pro Gerät sind keine Seltenheit, wird die Suche nach bestimmten Bildern immer schwieriger. Ist bei einem gesuchten Foto dessen Aufnahmedatum unbekannt, so kann es sehr lange dauern, bis es gefunden ist. Werden dem Nutzer zu viele Bilder auf einmal präsentiert, so geht der Überblick schnell verloren. Aus diesem Grund besteht eine typische Bildsuche heutzutage meist im endlosen Scrollen über viele Bildschirmseiten mit langen Bilderlisten.
Dieser Artikel stellt das Prinzip und die Funktionsweise der neuen iOS-App “Kiano” vor, die es Nutzern ermöglicht, alle ihre Bilder explorativ mittels visuellem Browsen zu erkunden. Der Name “Kiano” steht hierbei für “Keep Images Arranged & Neatly Organized”. Mit der App ist es außerdem möglich, zu einem Beispielbild gezielt nach ähnlichen Fotos auf dem Gerät zu suchen.
Um Bilder visuell durchsuch- und sortierbar zu machen, werden sogenannte Merkmalsvektoren bzw. Featurevektoren verwendet, die Aussehen und Inhalt von Bildern kompakt repräsentieren können. Zu einem Bild lassen sich ähnliche Bilder finden, indem die Bilder bestimmt werden, deren Featurevektoren eine geringe Distanz zum Featurevektor des Suchbildes haben.
Werden Bilder zweidimensional so angeordnet, dass die Featurevektoren benachbarter Bilder sehr ähnlich sind, so erhält man eine visuell sortierte Bilderlandkarte. Bei einer visuell sortierten Anordnung der Bilder fällt es Menschen deutlich leichter, mehr Bilder gleichzeitig zu erfassen, als dies im unsortierten Fall möglich wäre. Durch die graduelle Veränderung der Bildinhalte wird es möglich, über diese Karte visuell zu navigieren.
Generierung von Featurevektoren zur Bildbeschreibung
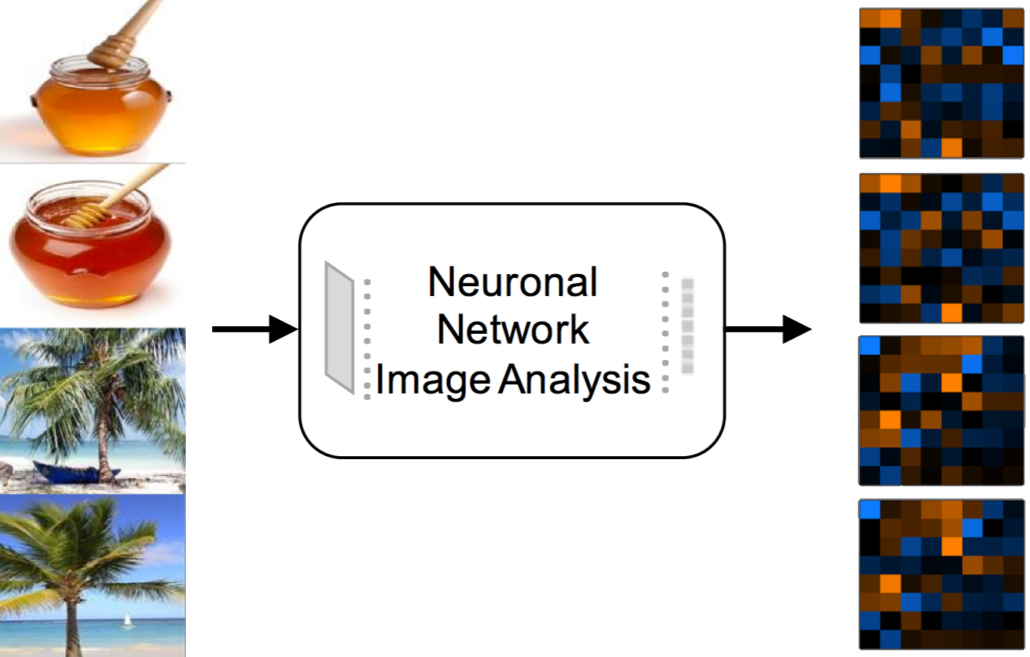
Convolutional Neural Networks (CNNs) sind nicht nur in der Lage, Bilder mit hoher Genauigkeit zu klassifizieren, d.h. zu erkennen, welches Objekt – entsprechend einer Menge von gelernten Objektkategorien auf einem Bild zu sehen ist, die Aktivierungen der Netzwerkschichten lassen sich auch als universelle Featurevektoren zur Bildbeschreibung nutzen. Während die vorderen Netzwerkschichten von CNNs einfache visuelle Bildmerkmale wie Farben und einfache Muster detektieren, repräsentieren die Ausgangsschichten des Netzwerks die semantischen Informationen bezüglich der gelernten Objektkategorien. Die Zwischenschichten des Netzwerks sind weniger von den Objektkategorien abhängig und können somit als generelle abstrakte Repräsentationen des Inhalts der Bilder angesehen werden. Hierbei ist es möglich, bereits fertig trainierte Klassifikationsnetzwerke für die Featureextraktion wiederzuverwenden. In der Visual Computing Gruppe der HTW Berlin wurden umfangreiche Evaluierungen durchgeführt, um zu bestimmen, welche Netzwerkschichten von welchen CNNs mit welchen zusätzlichen Transformationen zu verwenden sind, um aus Netzwerkaktivierungen Feature-Vektoren zu erzeugen, die sehr gut für die Suche nach beliebigen Bildern geeignet sind.
Beste Ergebnisse hinsichtlich der Suchgenauigkeit (der Mean Average Precision) wurden mit einem Deep Residual Learning Network (ResNet-200) erzielt. Die 2048 Aktivierungen vor dem vollvernetzten letzten Layer werden als initiale Featurevektoren verwendet, wobei sich die Suchgenauigkeit durch eine L1-Normierung, gefolgt von einer PCA-Transformation (Principal Component Analysis) sogar noch verbessern lässt. Hierdurch ist es möglich, die Featurevektoren auf eine Größe von nur 64 Bytes zu reduzieren. Leider ist die rechnerische Komplexität der Bestimmung dieser hochwertigen Featurevektoren zu groß, um sie auf mobilen Geräten verwenden zu können. Eine gute Alternative stellen die Mobilenets dar, die sich durch eine erheblich reduzierte Komplexität auszeichnen. Als Kompromiss zwischen Klassifikationsgenauigkeit und Komplexität wurde für die Kiano-App das Mobilenet_v2_0.5_128 verwendet. Die mit diesem Netzwerk bestimmten Featurevektoren wurden ebenfalls auf eine Größe von 64 Bytes reduziert.
 Die aus CNNs erzeugten Featurevektoren sind gut für die Suche nach Bildern mit ähnlichem Inhalt geeignet. Für die Suche nach Bilder, mit ähnlichen visuellen Eigenschaften (z.B. die auftretenden Farben oder deren örtlichen Verteilung) sind diese Featurevektoren nur bedingt geeignet. Hierfür eignen sich klassische sogenannte “Low-Level”-Featurevektoren besser. Da für eine ansprechende und leicht erfassbare Bildsortierung auch eine Übereinstimmung dieser visuellen Bildattribute wichtig ist, kommt bei Kiano ein weiterer Featurevektor zum Einsatz, mit dem sich diese “primitiven” visuellen Bildattribute beschreiben lassen. Dieser Featurevektor hat eine Größe von 50 Bytes. Bei Kiano kann der Nutzer in den Einstellungen wählen, ob bei der visuellen Sortierung und Bildsuche größerer Wert auf den Bildinhalt oder die visuelle Erscheinung eines Bildes gelegt werden soll.
Die aus CNNs erzeugten Featurevektoren sind gut für die Suche nach Bildern mit ähnlichem Inhalt geeignet. Für die Suche nach Bilder, mit ähnlichen visuellen Eigenschaften (z.B. die auftretenden Farben oder deren örtlichen Verteilung) sind diese Featurevektoren nur bedingt geeignet. Hierfür eignen sich klassische sogenannte “Low-Level”-Featurevektoren besser. Da für eine ansprechende und leicht erfassbare Bildsortierung auch eine Übereinstimmung dieser visuellen Bildattribute wichtig ist, kommt bei Kiano ein weiterer Featurevektor zum Einsatz, mit dem sich diese “primitiven” visuellen Bildattribute beschreiben lassen. Dieser Featurevektor hat eine Größe von 50 Bytes. Bei Kiano kann der Nutzer in den Einstellungen wählen, ob bei der visuellen Sortierung und Bildsuche größerer Wert auf den Bildinhalt oder die visuelle Erscheinung eines Bildes gelegt werden soll.
Visuelle Bildsortierung
Werden Bilder entsprechend ihrer Ähnlichkeiten sortiert angeordnet, so können mehrere hundert Bilder gleichzeitig wahrgenommen bzw. erfasst werden. Dies hilft, Regionen interessanter Bildern leichter zu erkennen und gesuchte Bilder schneller zu entdecken. Die Möglichkeit, viele Bilder gleichzeitig präsentieren zu können, ist neben Bildverwaltungssystemen besonders auch für E-Commerce-Anwendungen interessant.
Herkömmliche Dimensionsreduktionsverfahren, die hochdimensionale Featurevektoren auf zwei Dimensionen projizieren, sind für die Bildsortierung ungeeignet, da sie die Bilder so anordnen, dass Lücken und Bildüberlappungen entstehen. Sollen Bilder sortiert auf einem dichten regelmäßigen 2D-Raster angeordnet werden, kommen als Verfahren nur selbstorganisierende Karten oder selbstsortierende Karten in Frage.
Eine selbstorganisierende Karte (Self Organizing Map / SOM) ist ein künstliches neuronales Netzwerk, das durch unbeaufsichtigtes Lernen trainiert wird, um eine niedrigdimensionale, diskrete Darstellung der Daten des Eingangsraums als sogenannte Karte (Map) zu erzeugen. Im Gegensatz zu anderen künstlichen neuronalen Netzen, werden SOMs nicht durch Fehlerkorrektur, sondern durch ein Wettbewerbsverfahren trainiert, wobei eine Nachbarschaftsfunktion verwendet wird, um die lokalen Ähnlichkeiten der Eingangsdaten zu bewahren.
Eine selbstorganisierende Karte besteht aus Knoten, denen einerseits ein Gewichtsvektor der gleichen Dimensionalität wie die Eingangsdaten und anderseits eine Position auf der 2D-Karte zugeordnet sind. Die SOM-Knoten sind als zweidimensionales Rechteckgitter angeordnet. Das vom der SOM erzeugte Mapping ist diskret, da jeder Eingangsvektor einem bestimmten Knoten zugeordnet wird. Zu Beginn werden die Gewichtsvektoren aller Knoten mit Zufallswerten initialisiert. Wird ein hochdimensionaler Eingangsvektor in das Netz eingespeist, so wird dessen euklidischer Abstand zu allen Gewichtsvektoren berechnet. Der Knoten, dessen Gewichtsvektor dem Eingangsvektor am ähnlichsten ist, wird als Best Matching Unit (BMU) bezeichnet. Die Gewichte des BMU und seiner auf der Karte örtlich benachbarten Knoten werden an den Eingangsvektor angepasst. Dieser Vorgang wird iterativ wiederholt. Das Ausmaß dieser Anpassung nimmt im Laufe der Iterationen und der örtlichen Entfernung zum BMU-Knoten ab.
Um SOMs an die Bildsortierung anzupassen, sind zwei Modifikationen notwendig. Jeder Knoten darf nicht von mehr als einem Featurevektor (der ein Bild repräsentiert) ausgewählt werden. Eine Mehrfachauswahl würde zu einer Überlappung der Bilder führen. Aus diesem Grund muss die Anzahl der SOM-Knoten mindestens so groß wie die Anzahl der Bilder sein. Eine sinnvolle Erweiterung einer SOM verwendet ein Gitter, bei dem gegenüberliegende Kanten verbunden sind. Werden diese Torus-förmigen Karten für große SOMs verwendet, kann der Eindruck einer endlosen Karte erzeugt werden, wie es in Kiano umgesetzt ist. Ein Problem der SOMs ist ihre hohe rechnerische Komplexität, die quadratisch mit der Anzahl der zu sortierenden Bilder wächst, wodurch die maximale Anzahl an zu sortierenden Bildern beschränkt wird. Eine Lösung stellt eine selbstsortierende Karte (Self Sorting Map / SSM) dar, deren Komplexität nur n log(n) beträgt.
Selbstsortierende Karten beginnen mit einer zufälligen Positionierung der Bilder auf der Karte. Diese Karte wird dann in 4×4-Blöcke aufgeteilt und für jeden Block wird der Mittelwert der zugehörigen Featurevektoren bestimmt. Als nächstes werden aus 2×2 benachbarten Blöcken jeweils vier korrespondierende Bild-Featurevektoren untersucht und ihre zugehörigen Bilder gegebenenfalls getauscht. Aus den 4! = 24 Anordnungsmöglichkeiten wird diejenige gewählt, die die Summe der quadrierten Differenzen zwischen den jeweiligen Featurevektoren und den Featuremittelwerten der Blöcke minimiert. Nach mehreren Iterationen wird jeder Block in vier kleinere Blöcke halber Breite und Höhe aufgeteilt und wiederum in der beschriebenen Weise überprüft, wie die Bildpositionen dieser kleineren Blöcke getauscht werden sollten. Dieser Vorgang wird solange wiederholt, bis die Blockgröße auf 1×1 Bild reduziert ist.
In der Visual-Computing Gruppe der HTW Berlin wurde untersucht, wie die Sortierqualität des SSM-Algorithmus verbessert werden kann. Anstatt die Mittelwerte der Featurevektoren als konstanten Durchschnittsvektor für den gesamten Block zu berechnen, verwenden wir gleitende Tiefpassfilter, die sich effizient mittels Integralbildern berechnen lassen. Hierdurch entstehen weichere Übergänge auf der sortierten Bilderkarte. Weiterhin wird die Blockgröße nicht für mehrere Iterationen konstant gehalten, sondern kontinuierlich zusammen mit dem Radius des Filterkernels reduziert. Durch die Verwendung von optimierten Algorithmen von “Linear Assignment” Algorithmen wird es weiterhin möglich, den optimalen Positionstausch nicht nur für jeweils vier Featurevektoren bzw. Bildern sondern für eine deutlich größere Anzahl zu überprüfen. All diese Maßnahmen führen zu einer deutlich verbesserten Sortierungsqualität bei gleicher Komplexität.
Effiziente Umsetzung für iOS
Wie so oft, liegen die softwaretechnischen Herausforderungen an ganz anderen Stellen, als man zunächst vermutet. Für eine effiziente Implementierung der zuvor beschriebenen Algorithmen, insbesondere der SSM, stellte es sich heraus, dass die Programmiersprache Swift, in der iOS Apps normaler Weise entwickelt werden, erheblich mehr Rechenzeit benötigt, als eine Umsetzung in der Sprache C. Im Zuge der stetigen Weiterentwicklung von Swift und dessen Compiler mag sich die Lücke zu C zwar immer weiter schließen, zum Zeitpunkt der Umsetzung war die Implementierung in C aber um einen Faktor vier schneller als in Swift. Hierbei liegt die Vermutung nahe, dass der Zugriff auf und das Umsortieren von Featurevektoren als native C-Arrays deutlich effektiver passiert, als bei der Verwendung von Swift-Arrays. Da Swift-Arrays Value-Type sind, kommt es in Swift vermutlich zu unnötigen Kopieroperationen der Fließkommazahlen in den einzelnen Featurevektoren.
Die Berechnung des Mobilenet-Anteils der Featurevektoren konnte sehr komfortabel mit Apples CoreML Machine Learning Framework umgesetzt werden. Hierbei ist zu beachten, dass es sich wie oben beschrieben, nicht um eine Klassifikation handelt, sondern um das Abgreifen der Aktivierungen einer tieferen Schicht. Für Klassifikationen findet man praktisch sofort nutzbare Beispiele, für den Zugriff auf die Aktivierungen waren jedoch Anpassungen notwendig, die bei der Portierung eines vortrainierten Mobilenet nach CoreML vorgenommen wurden. Das stellte sich als erheblich einfacher heraus, als der Versuch, auf die tieferen Schichten eines Klassifizierungsnetzes in CoreML zuzugreifen.
Für die Verwaltung der Bilder, ihrer Featurevektoren und ihrer Position in der sortieren Karte wird in Kiano eine eigene Datenstruktur verwendet, die es zu persistieren gilt. Es ist dem Nutzer ja nicht zuzumuten, bei jedem Start der App auf die Berechnung aller Featurevektoren zu warten. Die Strategie ist es hierbei, bereits bekannte Bilder zu identifizieren und deren Features nur dann neu zu berechnen, falls sich das Bild verändert hat. Die über Appels Photos Framework zur Verfügung gestellten local Identifier identifizieren dabei die Bilder. Veränderungen werden über das Modifikationsdatum eines Bildes detektiert. Die größte Herausforderung ist hierbei das Zeichnen der Karte. Die Benutzerinteraktion soll schnell und flüssig erscheinen, auf Animationen wie das Nachlaufen der Karte beim Verschieben möchte man nicht verzichten. Die Umsetzung geschieht hierbei nicht in OpenGL ES, welches ab iOS 12 ohnehin als deprecated bezeichnet wird. Auf der anderen Seite wird aber auch nicht der „Standardweg“ des Überschreibens der draw-Methode einer Ableitung von UIView gewählt. Letztes führt bekanntlich zu Performanceeinbußen. Insbesondere deshalb, weil das System sehr oft Backing-Images der Ansichten erstellt. Um die Kontrolle über das Neuzeichnen zu behalten, wird in Kiano ein eigenes Backing-Image implementiert, das auf Ebene des Core Animation Frameworks dem View als Layer zugweisen wird. Diesem Layer kann dann sehr komfortabel eine 3D-Transformation zugewiesen werden und man profitiert von der GPU-Beschleunigung, ohne OpenGL ES direkt verwenden zu müssen.
Trotz der Verwendung eines Core Animation Layers ist das Zeichnen der Karte immer noch sehr zeitaufwendig. Das liegt an der Tatsache, dass je nach Zoomstufe tausende von Bildern darzustellen sind, die alle über das Photos Framework angefordert werden müssen. Das Nadelöhr ist dann weniger das Zeichnen, als die Zeit, die vergeht, bis einem das Bild zur Verfügung gestellt wird. Diese Vorgänge sind praktisch alle nebenläufig. Zur Erinnerung: Ein Foto kann in der iCloud liegen und zum Zeitpunkt der Anfrage noch gar nicht (oder noch nicht in geeigneter Auflösung) heruntergeladen sein. Netzwerkbedingt gibt es keine Vorhersage, wann oder ob überhaupt das Bild zur Verfügung gestellt wird. In Kiano werden zum einen Bilder in sehr kleiner Auflösung gecached, zum anderen wird beim Navigieren auf der Karte im Hintergrund ein neues Kartenteil als Backing-Image vorbereitet, das dem Nutzer nach Fertigstellung angezeigt wird. Die vorberechneten Kartenteile sind dabei drei Mal so breit und drei Mal so hoch wie das Display, so dass man diese „Hintergrundaktivität“ beim Verschieben der Karte in der Regel nicht bemerkt. Nur wenn die Bewegung zu schnell wird oder die Bilder zu langsam „geliefert“ werden, erkennt man schwarze Flächen, die sich dann verzögert mit Bildern füllen.
Vergleichbares passiert beim Hineinzoomen in die Karte. Der Nutzer sieht zunächst eine vergrößerte und damit unscharfe Version des aktuellen Kartenteils, während im Hintergrund ein Kartenteil in höherer Auflösung und mit weniger Bildern vorbereitet wird. In der Summe geht Kiano hier einen Kompromiss ein. Die Pixeldichte der Geräte würde eine schärfere Darstellung der Bilder auf der Karte erlauben. Allerdings müssten dann die Bilder in so höher Auflösung angefordert werden, dass eine flüssige Kartennavigation nicht mehr möglich wäre. So sieht der Nutzer in der Regel eine Karte mit Bildern in halber Auflösung gemessen an den physikalischen Pixeln seines Displays.
Ein anfangs unterschätzter Arbeitsaufwand bei der Umsetzung von Kiano liegt darin begründet, dass sich die Photo Library des Nutzers jederzeit während der Benutzung der App verändern kann. Bilder können durch Synchronisationen mit der iCloud oder mit iTunes verschwinden, sich in andere Alben bewegen, oder neue können auftauchen. Der Nutzer kann Bildschirmfotos machen. Das Photos Framework stellt komfortable Benachrichtigungen für solche Events zur Verfügung. Der Implementierung obliegt es dabei aber herauszubekommen, ob die Karte neu zu sortieren ist oder nicht, ob das gerade anzeigte Bild überhaupt noch existiert und was zu tun ist, wenn es verschwunden ist.
Zusammenfassend kann man feststellen, dass natürlich die Umsetzung der Algorithmen und die Darstellung dessen auf einer Karte zu den spannendsten Teilen der Arbeiten an Kiano zählen, dass aber der Umgang mit einer sich dynamisch ändernden Datenbasis nicht unterschätzt werden sollte.
Autoren
 Prof. Dr. Klaus Jung studierte Physik an der TU Berlin, wo er im Bereich der Mathematischen Physik promovierte. Bis 2008 arbeitete er als Leiter F&E bei der Firma LuraTech im Bereich der Dokumentenverarbeitung und Langzeitarchivierung. In der JPEG-Gruppe leitete er die deutsche Delegation bei der Standardisierung von JPEG2000. Seit 2008 ist er Professor für Medieninformatik an der HTW Berlin mit dem Schwerpunkt „Visual Computing“.
Prof. Dr. Klaus Jung studierte Physik an der TU Berlin, wo er im Bereich der Mathematischen Physik promovierte. Bis 2008 arbeitete er als Leiter F&E bei der Firma LuraTech im Bereich der Dokumentenverarbeitung und Langzeitarchivierung. In der JPEG-Gruppe leitete er die deutsche Delegation bei der Standardisierung von JPEG2000. Seit 2008 ist er Professor für Medieninformatik an der HTW Berlin mit dem Schwerpunkt „Visual Computing“.

Prof. Dr. Kai Uwe Barthel studierte Elektrotechnik an der TU Berlin, bevor er Assistent am Institut für Nachrichtentechnik wurde und im Bereich Bildkompression promovierte. Seit 2001 ist er Professor der HTW Berlin. Hauptforschungsbereiche sind visuelle Bildsuche und automatisches Bildverstehen. 2009 gründete er die pixolution GmbH www.pixolution.de, ein Unternehmen, das Technologien für die visuelle Bildsuche anbietet.




 Prof. Sven Buchholz hat eine Professur für die Fachgebiete Data Management und Data Mining am Fachbereich Informatik und Medien an der TH Brandenburg inne. Er ist wissenschaftlicher Leiter des an der Agentur für wissenschaftliche Weiterbildung und Wissenstransfer – AWW e. V. angesiedelten Projektes „Datenkompetenz 4.0 für eine digitale Arbeitswelt“ und Dozent des Vertiefungskurses „
Prof. Sven Buchholz hat eine Professur für die Fachgebiete Data Management und Data Mining am Fachbereich Informatik und Medien an der TH Brandenburg inne. Er ist wissenschaftlicher Leiter des an der Agentur für wissenschaftliche Weiterbildung und Wissenstransfer – AWW e. V. angesiedelten Projektes „Datenkompetenz 4.0 für eine digitale Arbeitswelt“ und Dozent des Vertiefungskurses „
![Rendered by QuickLaTeX.com \[ x = \begin{bmatrix} x_0\\ x_1\\ x_2\\ x_3\\ \vdots\\ x_n \end{bmatrix} \]](https://data-science-blog.com/wp-content/ql-cache/quicklatex.com-3a7aa03dea498a7231e3e497e3e5673d_l3.png)
![Rendered by QuickLaTeX.com \[ w = \begin{bmatrix} w_0\\ w_1\\ w_2\\ w_3\\ \vdots\\ w_n \end{bmatrix} \]](https://data-science-blog.com/wp-content/ql-cache/quicklatex.com-c70ad1733451ddc4512b23f2c739f80e_l3.png)
![Rendered by QuickLaTeX.com \[ x = \begin{bmatrix} 5\\ 12\\ 30\\ 2 \end{bmatrix} \]](https://data-science-blog.com/wp-content/ql-cache/quicklatex.com-97145f06e658d2f10086bd8c80293749_l3.png)
![Rendered by QuickLaTeX.com \[ w = \begin{bmatrix} 1\\ 2\\ 5\\ 12 \end{bmatrix} \]](https://data-science-blog.com/wp-content/ql-cache/quicklatex.com-6cd08615346cc16d7e8c23bac32c19b9_l3.png)
![Rendered by QuickLaTeX.com \[ z = w^T \cdot x = \big[1\text{ }2\text{ }5\text{ }12\big] \cdot \begin{bmatrix} 5\\ 12\\ 30\\ 2 \end{bmatrix} = 1 \cdot 5 + 2 \cdot 12 + 5 \cdot 30 + 12 \cdot 2 = 203 \]](https://data-science-blog.com/wp-content/ql-cache/quicklatex.com-70a3e9e9243199e97c549d1d9b0f44c0_l3.png)




 Alice Albrecht ist Research Engineer bei
Alice Albrecht ist Research Engineer bei