KNN: Künstliche Neuronen
Es gibt sehr ausführliche Definitionen und Abbildungen für ein künstliches Neuron, die in diesem Artikel aber nicht behandelt werden. Der Grund dafür ist pragmatischer Natur. Es soll eine gewisse Konsistenz zu den anderen KNN-Beiträgen dieser Reihe bestehen und das Thema soll nicht zu einer wissenschaftlichen Abhandlung mutieren.
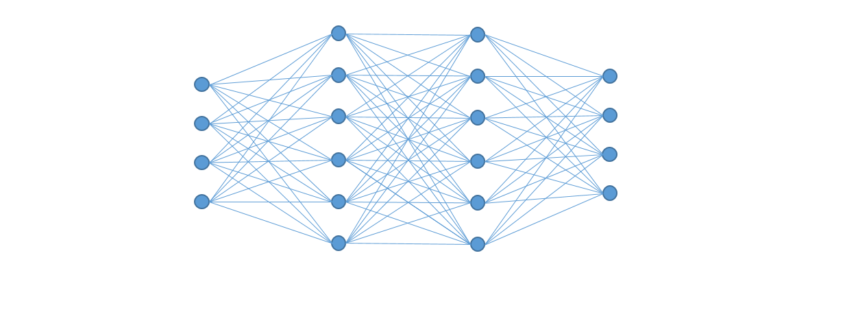
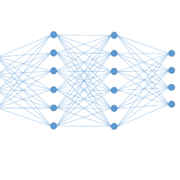
In dem Beitrag KNN: Was sind künstliche neuronale Netze geht es um den grundsätzlichen Aufbau von künstlichen neuronalen Netzwerken. Zusammengesetzt werden die Strukturen aus einer oftmals großen Anzahl von künstlichen Neuronen. Die nachfolgende Abbildung zeigt auf der Linken Seite einen extrahierten Ausschnitt aus einem Netzwerk. Es kann auch als einfaches allein stehendes Netzwerk betrachtet werden. Auf der rechten Seite ist eine allgemeingültigere Form zu sehen. Die Bias Unit (VB) wird üblicherweise als X0 bezeichnet und hat immer den Wert 1.
 |
 |
Um den Ausgangswert Y zu berechnen wird zunächst jeder Eingangswert X mit seinem dazugehörigen Gewicht ![]() (Theta) multipliziert und die Ergebnisse aufsummiert. Das Zwischenergebnis ist die Aktivierungsstärke z:
(Theta) multipliziert und die Ergebnisse aufsummiert. Das Zwischenergebnis ist die Aktivierungsstärke z:
![]()
Im nächsten Schritt wird der eigentliche Ausgangswert Y errechnet, indem die Aktivierungsstärke z an eine Aktivierungsfunktion angelegt wird. Es gibt zwar verschiedene Funktionen, häufig wird aber die Logistische bzw. Sigmoid-Funktion verwendet. Sie ist nicht-linear und hat einen Ausgangswertebereich zwischen 0 und 1.
 |
|
Wird das Bias Neuron und sein Gewicht nicht beachtet, bestimmen die eingehenden Daten die Aktivierungsstärke und damit den Ausgang der Funktion. Unter Verwendung der Bias Unit verschiebt sich die Funktion entlang der Y-Achse, was einer Verschiebung von einem Schwellwert gleich kommt.
Die endgültige Formel für die Aktivierung eines Neurons sieht sehr ähnlich zu der Logistischen Regression aus. Werden die Werte von X und Theta zu Vektoren zusammengefasst, lässt sich die Berechnung stark vereinfachen:
![]()
Als Programmcode müsste diese Berechnung dennoch mit einer Schleife realisiert werden oder noch besser mit einer Bibliothek für lineare Algebra.
Ähnliche Artikel:
• KNN: Was sind künstliche neuronale Netze
• KNN: Vorteile und Nachteile





Trackbacks & Pingbacks
[…] Wenn die Gewichte eines künstlichen neuronalen Netzwerkes trainiert sind, kann es verwendet werden, um Vorhersagen über eine am Eingang angelegte Beobachtung zu treffen. Hierzu werden Schicht für Schicht, in einem sogenannten Vorwärtspass (Forward-Pass), die Aktivierungen der einzelnen Neuronen ermittelt, bis ein Ergebnis an der Ausgabeschicht anliegt. Der ganze Prozess hat zwar einen eigenen Namen (Vorwärtspass), ist aber im Endeffekt nur ein iteratives durchführen von mehreren logistischen Regressionen und entspricht dem Vorgehen aus dem Artikel „KNN: künstliche Neuronen“. […]
[…] Wenn die Gewichte eines künstlichen neuronalen Netzwerkes trainiert sind, kann es verwendet werden, um Vorhersagen über eine am Eingang angelegte Beobachtung zu treffen. Hierzu werden Schicht für Schicht, in einem sogenannten Vorwärtspass (Forward-Pass), die Aktivierungen der einzelnen Neuronen ermittelt, bis ein Ergebnis an der Ausgabeschicht anliegt. Der ganze Prozess hat zwar einen eigenen Namen (Vorwärtspass), ist aber im Endeffekt nur ein iteratives durchführen von mehreren logistischen Regressionen und entspricht dem Vorgehen aus dem Artikel „KNN: künstliche Neuronen“. […]
[…] Wenn die Gewichte eines künstlichen neuronalen Netzwerkes trainiert sind, kann es verwendet werden, um Vorhersagen über eine am Eingang angelegte Beobachtung zu treffen. Hierzu werden Schicht für Schicht, in einem sogenannten Vorwärtspass (Forward-Pass), die Aktivierungen der einzelnen Neuronen ermittelt, bis ein Ergebnis an der Ausgabeschicht anliegt. Der ganze Prozess hat zwar einen eigenen Namen (Vorwärtspass), ist aber im Endeffekt nur ein iteratives durchführen von mehreren logistischen Regressionen und entspricht dem Vorgehen aus dem Artikel „KNN: künstliche Neuronen“. […]
[…] Wenn die Gewichte eines künstlichen neuronalen Netzwerkes trainiert sind, kann es verwendet werden, um Vorhersagen über eine am Eingang angelegte Beobachtung zu treffen. Hierzu werden Schicht für Schicht, in einem sogenannten Vorwärtspass (Forward-Pass), die Aktivierungen der einzelnen Neuronen ermittelt, bis ein Ergebnis an der Ausgabeschicht anliegt. Der ganze Prozess hat zwar einen eigenen Namen (Vorwärtspass), ist aber im Endeffekt nur ein iteratives durchführen von mehreren logistischen Regressionen und entspricht dem Vorgehen aus dem Artikel „KNN: künstliche Neuronen“. […]
[…] Inspiration für das Software-Neuron siehe Abbildung unten rechts. Beim mathematischen Modell eines Software-Neurons (Künstliches Neuron eines KNN) wird davon ausgegangen, dass die verschiedenen Dendriten unterschiedlich stark ausgeprägt sind und […]
Leave a Reply
Want to join the discussion?Feel free to contribute!