IIIa. Einführung in TensorFlow: Realisierung eines Perzeptrons mit TensorFlow
1. Einleitung
1.1. Was haben wir vor?
Im zweiten Artikel dieser Serie sind wir darauf eingegangen, wie man TensorFlow prinzipiell nutzt. Wir wollen das Gelernte an einem einfachen Modell anwenden. Bevor wir dies jedoch tun, müssen wir die Theorie hinter dem Modell verstehen um TensorFlow richtig anwenden zu können.
Dafür bietet sich ein Adaline-Perzeptron sehr gut an. Es ist ein einfaches Modell mit nur einer Schicht, wo die Theorie verständlich ist.
1.2. Aufgabenstellung
 Label 0, Rot
Label 0, Rot  Label 1
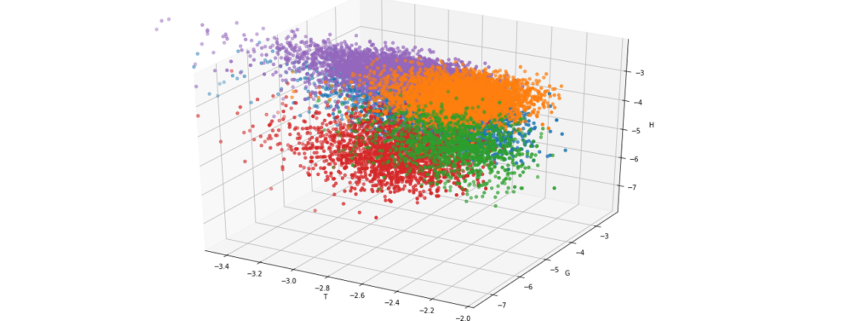
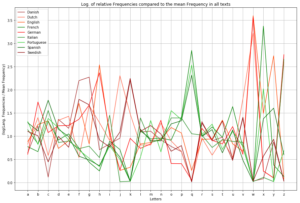
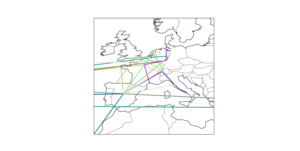
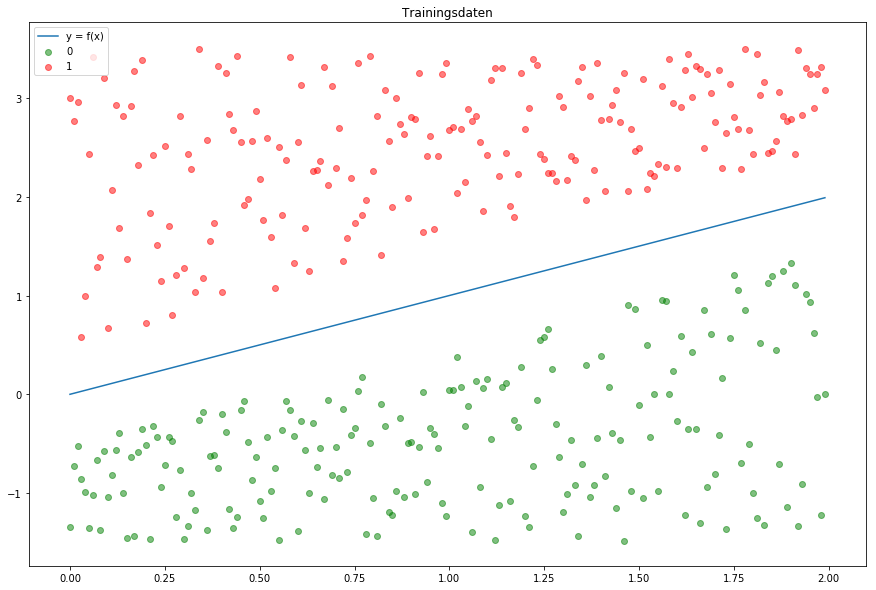
Label 1In Abb.1 sehen wir unsere Trainingsdaten, die
zufällig generiert wurden. Alle grün markierten Datenpunkte haben das Label 0 und die rot markierten Punkte erhalten das Label 1.
Wir möchten einen Adaline-Perzeptron entwickeln, der unsere Daten je nach Position in die richtige Klasse zuordnet. Somit haben wir eine Aufgabe mit binärer Klassifikation
2. Grundlagen
2.1. Funktionsweise eines Perzeptrons
Ein Perzeptron ist ein mathematisches Modell, welches eine Nervenzelle beschreiben soll.
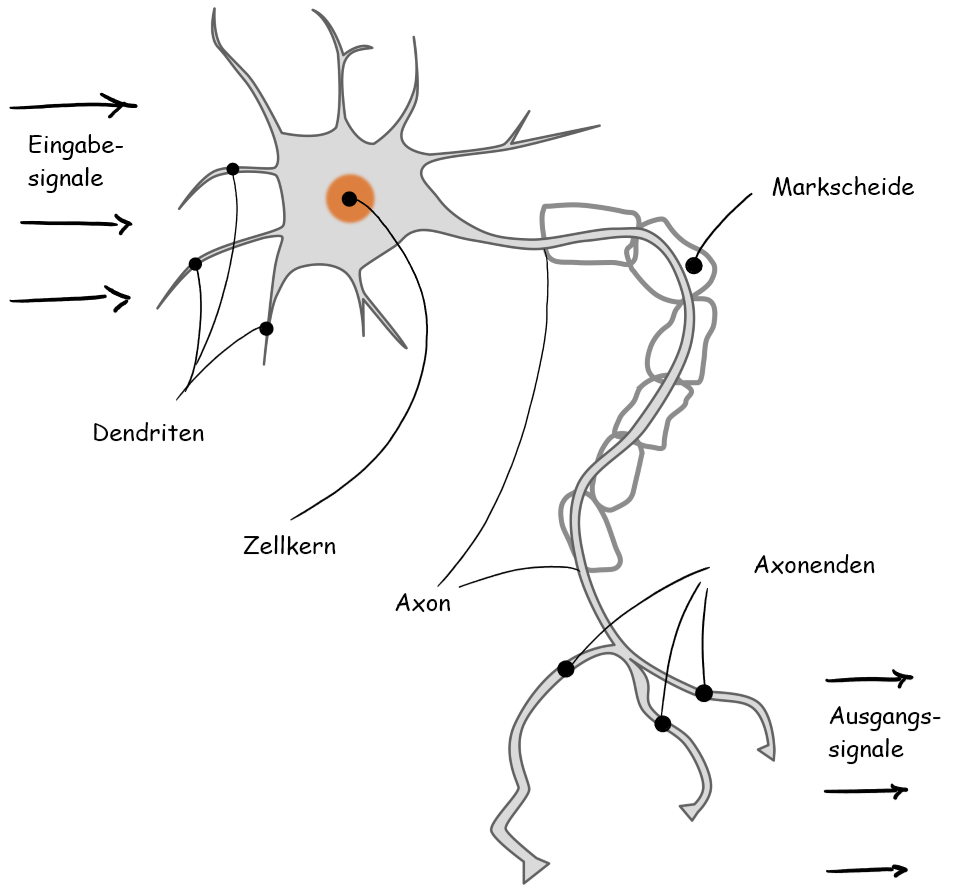
Vereinfacht funktioniert eine Nervenzelle, auch Neuron genannt, folgendermaßen: Eine Vielzahl von Reizen bzw. Eingabesignalen wird von den Dendriten aufgenommen, die dann im Kern verarbeitet werden. Wenn die verschiedenen Eingabesignale die ’richtige’ Dosis an Reizen erreichen und einen Schwellwert erreichen, dann feuert das Neuron ab und leitet ein Signal weiter.
Für eine detaillierte Beschreibung, wie ein Perzeptron mathematisch beschrieben wird, möchte ich auf diesen Artikel hinweisen.
Wir wollen uns in diesem Artikel auf den Adaline-Algorithmus (ADAptive LINear Element) konzentrieren. Dieser ist eine Weiterentwicklung des Perzeptron. Die Besonderheit an diesem Algorithmus liegt darin, dass das Konzept der Fehlerminimierung durch Minimierung der Straffunktion der berechneten und der tatsächlichen Ergebnisse enthält. Ein weiter wesentlicher Unterschied zu einem einfachen Perzeptron ist vor allem, dass wir bei Adaline keine einfache Sprungfunktion als Aktivierungsfunktion haben, sondern eine stetige Funktion nutzen und somit eine Differenzierung/Ableitung der Aktivierungsfunktion durchführen können. Dieser Punkt ist für die Optimierung der Gewichte und des Lernens unseres Modells ein entscheidender Vorteil.
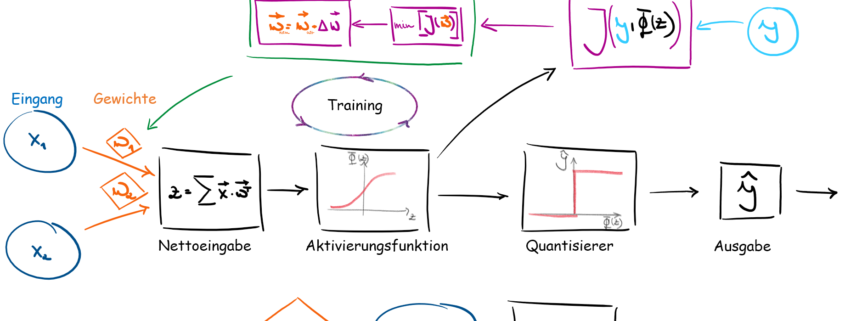
Das Schema in Abb.3 zeigt uns die Funktionsweise, wie unser Adaline-Algorithmus funktionieren soll.
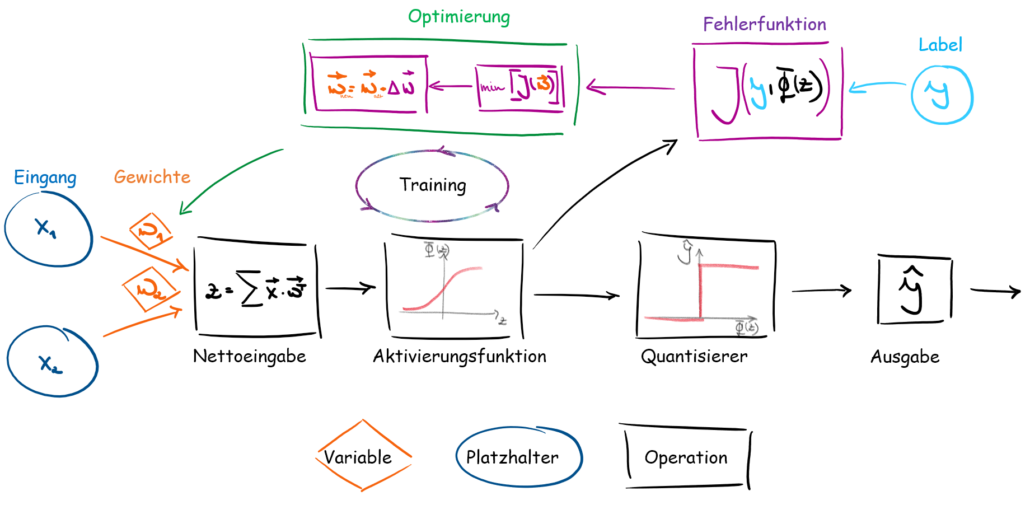
- Eingang: In dieser Schicht werden unsere Daten ein gepfangen und weitergeleitet
- Die Gewichte geben an, welchen Einfluss unsere Eingangssignale haben. Sie sind auch unsere Größe, die in unserem Algorithmus optimiert werden.
- Die Nettoeingabefunktion wird durch die Zusammenführung von Eingangssignalen und Gewichten erzeugt. Je nachdem wie die Eingänge und Gewichte verbunden sind, müssen diese mathematisch korrekt multipliziert werden.
- Die Nettoeingabe wird dann, in die Aktivierungsfunktion eingebunden. Je nachdem welche Aktivierungsfunktion man nutzt, ändert sich die Ausgabe nach der Aktivierungsfunktion.
- In der Fehlerrückgabe werden die vorhergesagten Ausgaben mit den tatsächlichen Werten/Labels verglichen. Auch hier gibt es verschiedene Verfahren, um eine Fehlerfunktion zu bilden.
- In der Optimierung werden dann auf Basis der Fehlerfunktion die Gewichte so optimiert, dass der Fehler zwischen unseren Label und den vorhergesagten Werten minimiert wird.
- Der Quantisierer ist ein optionales Element. Bei einer kategorischen Problemstellung bekommen wir nach der Aktivierungsfunktion eine Wahrscheinlichkeit zu der die Daten zu welchem Label zugeteilt werden. Der Quantisierer wandelt diese Wahrscheinlichkeiten zu Labeln um. Zum Beispiel haben wir einen Datensatz und unser Modell sagt voraus, dass dieser Datensatz zu 88 % das Label 1 hat. Je nachdem welche Grenze dem Quantisierer gegeben wird, teilt dieser dann den Datensatz in die entsprechende Klasse ein. Wenn wir sagen die Grenze soll 50% sein, dann sagt der Quantisierer, dass unser Datensatz Label 1 ist.
2.2. Aktivierungsfunktionen
Die Aktivierungsfunktion ist ein sehr wichtiger Bestandteil bei neuronalen Netzen. Diese bestimmen, wie sich das Ausgangssignal verhält. Es gibt eine Vielzahl von Aktivierungsfunktionen, die ihre Vor- und Nachteile haben. Wir wollen uns erstmal auf die Sigmoidfunktion konzentrieren.
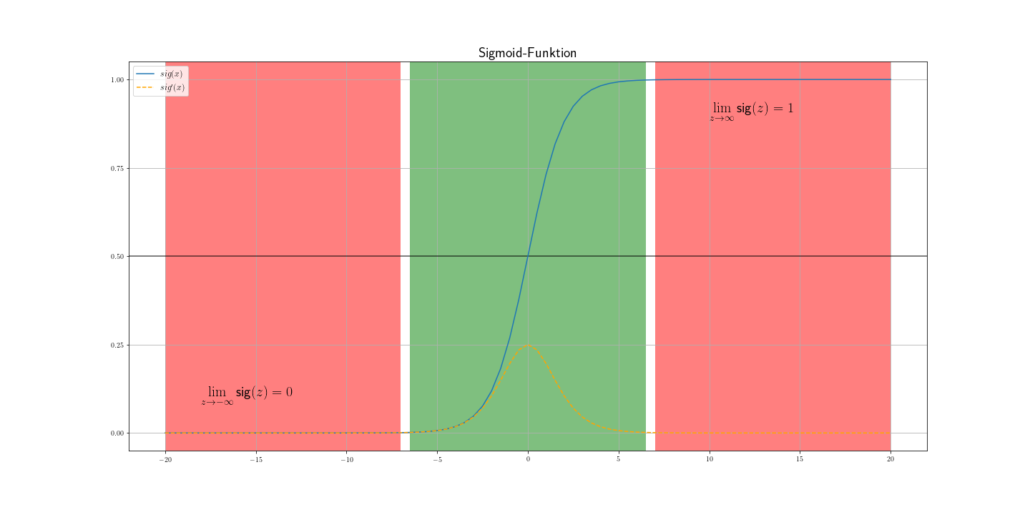
Eigentlich haben wir bei der Sprungfunktion alles was wir brauchen. Wenn wir einen Schwellenwert erreichen ![]() , dann feuert die Sprungfunktion und das sehr abrupt. Die Sigmoidfunktion hingegen hat einen sanfteren und natürlicheren Verlauf als die Sprungfunktion. Außerdem ist sie eine stetig und differenzierbare Funktion, was sehr vorteilhaft für das Gradientenverfahren (Optimierung) ist. Daher wollen wir die Sigmoidfunktion für unsere Problemstellung nutzen.
, dann feuert die Sprungfunktion und das sehr abrupt. Die Sigmoidfunktion hingegen hat einen sanfteren und natürlicheren Verlauf als die Sprungfunktion. Außerdem ist sie eine stetig und differenzierbare Funktion, was sehr vorteilhaft für das Gradientenverfahren (Optimierung) ist. Daher wollen wir die Sigmoidfunktion für unsere Problemstellung nutzen.
![]()
2.3. Optimierungsverfahren
2.3.1. Fehlerfunktion
Die wohl am häufigsten genutzten Fehlerfunktionen (oder auch Ziel-, Kosten-, Verlust-, Straffunktion) sind wohl der mittlere quadratische Fehler bei Regressionen und die Kreuzentropie bei kategorischen Daten.
In unserem Beispiel haben wir Daten kategorischer Natur und eine binäre Thematik, weshalb wir uns auf die Kreuzentropie in Kombination mit der Sigmoidfunktion konzentrieren wollen.
Aus der Matrizenrechnung ![]() erhalten wir ein Skalar (eindimensional). Geben wir diese in die Sigmoidfunktion ein, kommen wir auf folgende Gleichung.
erhalten wir ein Skalar (eindimensional). Geben wir diese in die Sigmoidfunktion ein, kommen wir auf folgende Gleichung.
![]()
Hinweis: Wie in Abb.4 kann die Sigmoidfunktion nur Werte zwischen 0 und 1 erreichen, ohne diese jemals zu erreichen. Außerdem ändert sich die Funktion bei sehr großen Beträgen nur noch minimal, man spricht auch von Sättigung. Dieser Fakt ist sehr wichtig, wenn um die Optimierung der Gewichte geht. Wenn wir unsere Nettoeingabe nicht skalieren, dann kann es passieren, dass unser Modell sehr langsam lernt, da der Gradient der Sigmoidfunktion bei großen Beträgen sehr klein ist.
Bei Aufgaben mit binärer Klassifizierung hat sich die Kreuzentropie als Fehlerfunktion etabliert. Sie ist ein Maß für die Qualität eines Modells, welche eine Wahrscheinlichkeitsverteilung angibt. Je kleiner diese Größe ist, desto besser unser Modell. Es gilt also unsere Fehlerfunktion zu minimieren!
Wir wollen in einem separaten Artikel genauer auf die Kreuzentropie eingehen. Für den jetzigen Zeitpunkt soll es reichen, wenn wir die Formel vor Augen haben und was sie grob bedeutet.
![]() sei die ‘wahre’ Wahrscheinlichkeitsverteilung aus der Menge
sei die ‘wahre’ Wahrscheinlichkeitsverteilung aus der Menge ![]() , in unserem Fall, die Wahrscheinlichkeitsverteilung, ob ein Datenpunkt dem Label 0 oder 1 zugehört. Wenn wir nun unser Eingangssignal durch die Aktivierungsfunktion fließen lassen, dann erhalten wir ebenfalls eine ‘berechnete’ Wahrscheinlichkeitsverteilung die
, in unserem Fall, die Wahrscheinlichkeitsverteilung, ob ein Datenpunkt dem Label 0 oder 1 zugehört. Wenn wir nun unser Eingangssignal durch die Aktivierungsfunktion fließen lassen, dann erhalten wir ebenfalls eine ‘berechnete’ Wahrscheinlichkeitsverteilung die ![]() genannt werden soll. Um die Wahrscheinlichkeitsverteilungen
genannt werden soll. Um die Wahrscheinlichkeitsverteilungen ![]() und
und ![]() zu vergleichen, nutzen wir die Kreuzentropie, welche wie folgt für diskrete Daten definiert ist:
zu vergleichen, nutzen wir die Kreuzentropie, welche wie folgt für diskrete Daten definiert ist:
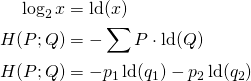
Beispiel einer binären Problemstellung. Wir haben unsere Label 0 und 1. ![]() ist die Wahrscheinlichkeit, inwiefern unser Datenpunkt das Label 0 hat. Da wir die Trainingsdaten kennen, wissen wir auch das dieser Punkt zu 100 %, welches Label hat. Unser Modell hat zum Beispiel im ersten Durchgang eine Wahrscheinlichkeit von 0.8 und später 0.9 berechnet.
ist die Wahrscheinlichkeit, inwiefern unser Datenpunkt das Label 0 hat. Da wir die Trainingsdaten kennen, wissen wir auch das dieser Punkt zu 100 %, welches Label hat. Unser Modell hat zum Beispiel im ersten Durchgang eine Wahrscheinlichkeit von 0.8 und später 0.9 berechnet.
Fall I : ![]() Die Wahrscheinlichkeitsverteilungen P und Q sind identisch:
Die Wahrscheinlichkeitsverteilungen P und Q sind identisch:
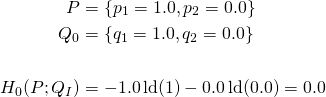
Fall II: ![]() Die Wahrscheinlichkeitsverteilungen P und Q sind nicht identisch:
Die Wahrscheinlichkeitsverteilungen P und Q sind nicht identisch:
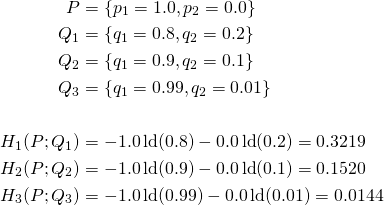
In der oberen Berechnung haben wir zum einfachen Verständnis der Kreuzentropie ein einfaches Beispiel. ![]() ist eine 100 % ige Wahrscheinlichkeit, dass zum Beispiel unser Datensatz das Label 0 hat. Unser perfektes Modell mit
ist eine 100 % ige Wahrscheinlichkeit, dass zum Beispiel unser Datensatz das Label 0 hat. Unser perfektes Modell mit ![]() hat eine Kreuzentropie-Wert von 0. Unser zweites Modell
hat eine Kreuzentropie-Wert von 0. Unser zweites Modell ![]() hat eine gewisse Unbestimmtheit, die sich durch eine größere Kreuzentropie
hat eine gewisse Unbestimmtheit, die sich durch eine größere Kreuzentropie ![]() bemerkbar macht. Je mehr sich also unser Modell von den wirklichen Daten abweicht, desto größer ist die Kreuzentropie.
bemerkbar macht. Je mehr sich also unser Modell von den wirklichen Daten abweicht, desto größer ist die Kreuzentropie.
2.3.2. Optimierung nach dem Gradientenverfahren
Wenn wir es also schaffen die Kreuzentropie zu minimieren, dann erhalten wir auch ein besseres Modell! Bei der Optimierung nach dem Gradientenverfahren versuchen wir uns schrittweise an das Minimum zu bewegen.
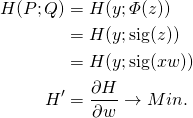
Ziel der Optimierung ist es, dass unsere Gewichte so angepasst werden, dass sich der Fehler in unserer Fehlerfunktion minimiert. Wir leiten also die Fehlerfunktion nach ![]() ab.
ab.
Diese Aufgabe wird zum Glück von TensorFlow übernommen und wir müssen die Randbedingungen nur dem System geben.
Neben dem Gradientenverfahren, gibt es auch noch eine Menge anderer Optimierer, auf die wir später nochmal eingehen werden.
3. Zusammenfassung
Bevor wir TensorFlow nutzen, ist es wichtig, dass wir unser Modell verstehen. TensorFlow ist wie vieles nur ein Werkzeug, wenn man die Grundlagen nicht verstanden hat. Daher haben wir uns in diesem Artikel erstmal auf die Theorie konzentriert und ich habe dabei versucht mich auf das Wesentliche zu beschränken.
Im nächsten Artikel werden wir dann unser Modell in TensorFlow realisieren.
PS: In einem separaten Artikel wollen später nochmal detaillierter auf Aktivierungsfunktion, Kreuzentropie und das Gradientenverfahren eingehen.