Über die Integration symbolischer Inferenz in tiefe neuronale Netze

Tiefe neuronale Netze waren in den letzten Jahren eine enorme Erfolgsgeschichte. Viele Fortschritte im Bereich der KI, wie das Erkennen von Objekten, die fließende Übersetzung natürlicher Sprache oder das Spielen von GO auf Weltklasseniveau, basieren auf tiefen neuronalen Netzen. Über die Grenzen dieses Ansatzes gab es jedoch nur wenige Berichte. Eine dieser Einschränkungen ist die Unfähigkeit, aus einer kleinen Anzahl von Beispielen zu lernen. Tiefe neuronale Netze erfordern in der Regel eine Vielzahl von Trainingsbeispielen, während der Mensch aus nur einem einzigen Beispiel lernen kann. Wenn Sie eine Katze einem Kind zeigen, das noch nie zuvor eine gesehen hat, kann es eine weitere Katze anhand dieser einzigen Instanz erkennen. Tiefe neuronale Netze hingegen benötigen Hunderttausende von Bildern, um zu erlernen, wie eine Katze aussieht. Eine weitere Einschränkung ist die Unfähigkeit, Rückschlüsse aus bereits erlerntem Allgemeinwissen zu ziehen. Beim Lesen eines Textes neigen Menschen dazu, weitreichende Rückschlüsse auf mögliche Interpretationen des Textes zu ziehen. Der Mensch ist dazu in der Lage, weil er Wissen aus sehr unterschiedlichen Bereichen abrufen und auf den Text anwenden kann.

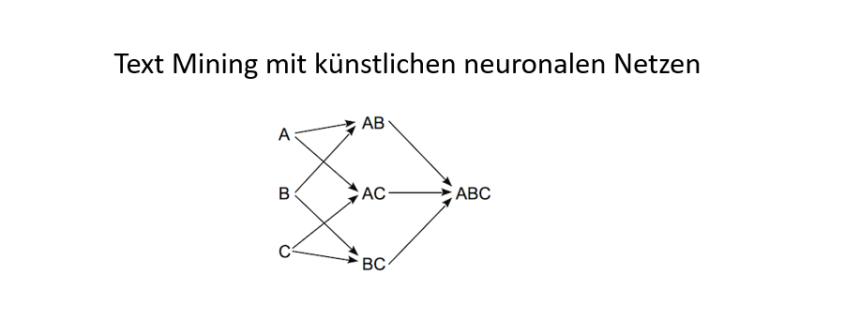
Diese Einschränkungen deuten darauf hin, dass in tiefen neuronalen Netzen noch etwas Grundsätzliches fehlt. Dieses Etwas ist die Fähigkeit, symbolische Bezüge zu Entitäten in der realen Welt herzustellen und sie in Beziehung zueinander zu setzen. Symbolische Inferenz in Form von formaler Logik ist seit Jahrzehnten der Kern der klassischen KI, hat sich jedoch als spröde und komplex in der Anwendung erwiesen. Gibt es dennoch keine Möglichkeit, tiefe neuronale Netze so zu verbessern, dass sie in der Lage sind, symbolische Informationen zu verarbeiten? Tiefe neuronale Netzwerke wurden von biologischen neuronalen Netzwerken wie dem menschlichen Gehirn inspiriert. Im Wesentlichen sind sie ein vereinfachtes Modell der Neuronen und Synapsen, die die Grundbausteine des Gehirns ausmachen. Eine solche Vereinfachung ist, dass statt mit zeitlich begrenzten Aktionspotenzialen nur mit einem Aktivierungswert gearbeitet wird. Aber was ist, wenn es nicht nur wichtig ist, ob ein Neuron aktiviert wird, sondern auch, wann genau. Was wäre, wenn der Zeitpunkt, zu dem ein Neuron feuert, einen relationalen Kontext herstellt, auf den sich diese Aktivierung bezieht? Nehmen wir zum Beispiel ein Neuron, das für ein bestimmtes Wort steht. Wäre es nicht sinnvoll, wenn dieses Neuron jedes Mal ausgelöst würde, wenn das Wort in einem Text erscheint? In diesem Fall würde das Timing der Aktionspotenziale eine wichtige Rolle spielen. Und nicht nur das Timing einer einzelnen Aktivierung, sondern auch das Timing aller eingehenden Aktionspotenziale eines Neurons relativ zueinander wäre wichtig. Dieses zeitliche Muster kann verwendet werden, um eine Beziehung zwischen diesen Eingangsaktivierungen herzustellen. Wenn beispielsweise ein Neuron, das ein bestimmtes Wort repräsentiert, eine Eingabesynapse für jeden Buchstaben in diesem Wort hat, ist es wichtig, dass das Wort Neuron nur dann ausgelöst wird, wenn die Buchstabenneuronen in der richtigen Reihenfolge zueinander abgefeuert wurden. Konzeptionell könnten diese zeitlichen Unterschiede als Relationen zwischen den Eingangssynapsen eines Neurons modelliert werden. Diese Relationen definieren auch den Zeitpunkt, zu dem das Neuron selbst im Verhältnis zu seinen Eingangsaktivierungen feuert. Aus praktischen Gründen kann es sinnvoll sein, der Aktivierung eines Neurons mehrere Slots zuzuordnen, wie z.B. den Anfang und das Ende eines Wortes. Andernfalls müssten Anfang und Ende eines Wortes als zwei getrennte Neuronen modelliert werden. Diese Relationen sind ein sehr mächtiges Konzept. Sie ermöglichen es, die hierarchische Struktur von Texten einfach zu erfassen oder verschiedene Bereiche innerhalb eines Textes miteinander in Beziehung zu setzen. In diesem Fall kann sich ein Neuron auf eine sehr lokale Information beziehen, wie z.B. einen Buchstaben, oder auf eine sehr weitreichende Information, wie z.B. das Thema eines Textes.

Eine weitere Vereinfachung im Hinblick auf biologische neuronale Netze besteht darin, dass mit Hilfe einer Aktivierungsfunktion die Feuerrate eines einzelnen Neurons angenähert wird. Zu diesem Zweck nutzen klassische neuronale Netze die Sigmoidfunktion. Die Sigmoidfunktion ist jedoch symmetrisch bezüglich großer positiver oder negativer Eingangswerte, was es sehr schwierig macht, ausssagenlogische Operationen mit Neuronen mit der Sigmoidfunktion zu modellieren. Spiking-Netzwerke hingegen haben einen klaren Schwellenwert und ignorieren alle Eingangssignale, die unterhalb dieses Schwellenwerts bleiben. Daher ist die ReLU-Funktion oder eine andere asymmetrische Funktion eine deutlich bessere Annäherung für die Feuerrate. Diese Asymmetrie ist auch für Neuronen unerlässlich, die relationale Informationen verarbeiten. Das Neuron, das ein bestimmtes Wort repräsentiert, muss nämlich für alle Zeitpunkte, an denen das Wort nicht vorkommt, völlig inaktiv bleiben.

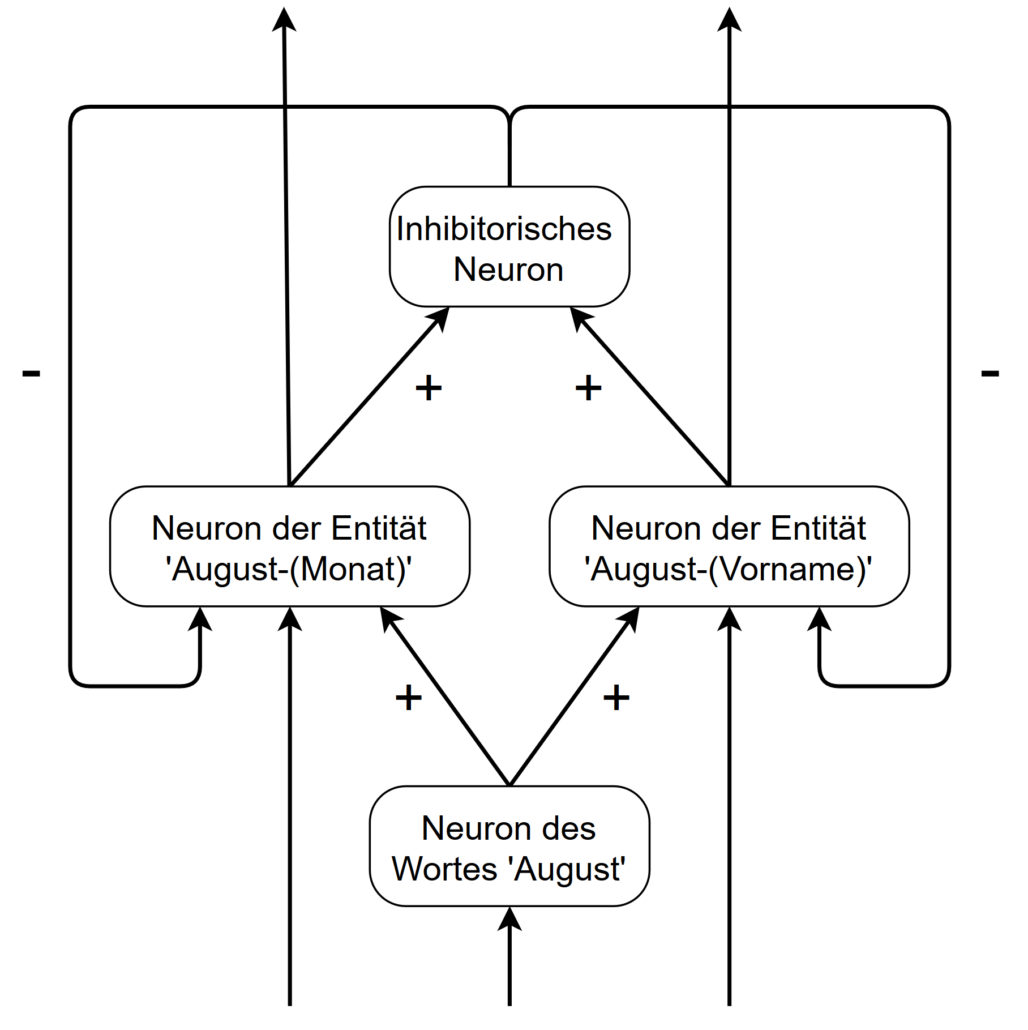
Ebenfalls vernachlässigt wird in tiefen neuronalen Netzwerken die Tatsache, dass verschiedene Arten von Neuronen in der Großhirnrinde vorkommen. Zwei wichtige Typen sind die bedornte Pyramidenzelle, die in erster Linie eine exzitatorische Charakteristik aufweist, und die nicht bedornte Sternzelle, die eine hemmende aufweist. Die inhibitorischen Neuronen sind besonders, weil sie es ermöglichen, negative Rückkopplungsschleifen aufzubauen. Solche Rückkopplungsschleifen finden sich normalerweise nicht in einem tiefen neuronalen Netzwerk, da sie einen inneren Zustand in das Netzwerk einbringen. Betrachten wir das folgende Netzwerk mit einem hemmenden Neuron und zwei exzitatorischen Neuronen, die zwei verschiedene Bedeutungen des Wortes “August” darstellen.

Beide Bedeutungen schließen sich gegenseitig aus, so dass das Netzwerk nun zwei stabile Zustände aufweist. Diese Zustände können von weiteren Eingangssynapsen der beiden exzitatorischen Neuronen abhängen. Wenn beispielsweise das nächste Wort nach dem Wort ‘August’ ein potenzieller Nachname ist, könnte eine entsprechende Eingabesynapse für das Entitätsneuron August-(Vorname) das Gewicht dieses Zustands erhöhen. Es ist nun wahrscheinlicher, dass das Wort “August” als Vorname und nicht als Monat eingestuft wird. Aber bedenken Sie, dass beide Zustände evaluiert werden müssen. In größeren Netzwerken können viele Neuronen durch negative oder positive Rückkopplungsschleifen verbunden sein, was zu einer großen Anzahl von stabilen Zuständen im Netzwerk führen kann.

Aus diesem Grund ist ein effizienter Optimierungsprozess erforderlich, der den besten Zustand in Bezug auf eine Zielfunktion ermittelt. Diese Zielfunktion könnte darin bestehen, die Notwendigkeit der Unterdrückung stark aktivierter Neuronen zu minimieren. Diese Zustände haben jedoch den enormen Vorteil, dass sie es erlauben, unterschiedliche Interpretationen eines bestimmten Textes zu berücksichtigen. Es ist eine Art Denkprozess, in dem verschiedene Interpretationen bewertet werden und die jeweils stärkste als Ergebnis geliefert wird. Glücklicherweise lässt sich die Suche nach einem optimalen Lösungszustand recht gut optimieren.

Der Grund, warum wir in diesen Rückkopplungsschleifen hemmende Neuronen benötigen, ist, dass sonst alle gegenseitig unterdrückenden Neuronen vollständig miteinander verbunden sein müssten. Das würde zu einer quadratisch zunehmenden Anzahl von Synapsen führen.

Durch die negativen Rückkopplungsschleifen, d.h. durch einfaches Verbinden einer negativen Synapse mit einem ihrer Vorläuferneuronen, haben wir plötzlich den Bereich der nichtmonotonen Logik betreten. Die nichtmonotone Logik ist ein Teilgebiet der formalen Logik, in dem Implikationen nicht nur zu einem Modell hinzugefügt, sondern auch entfernt werden. Es wird davon ausgegangen, dass eine nichtmonotone Logik erforderlich ist, um Schlussfolgerungen für viele Common Sense Aufgaben ziehen zu können. Eines der Hauptprobleme der nichtmonotonen Logik ist, dass sie oft nicht entscheiden kann, welche Schlussfolgerungen sie ziehen soll und welche eben nicht. Einige skeptische oder leichtgläubige Schlussfolgerungen sollten nur gezogen werden, wenn keine anderen Schlussfolgerungen wahrscheinlicher sind. Hier kommt die gewichtete Natur neuronaler Netze zum Tragen. In neuronalen Netzen können nämlich eher wahrscheinliche Zustände weniger wahrscheinliche Zustände unterdrücken.

Beispielimplementierung innerhalb des Aika-Frameworks

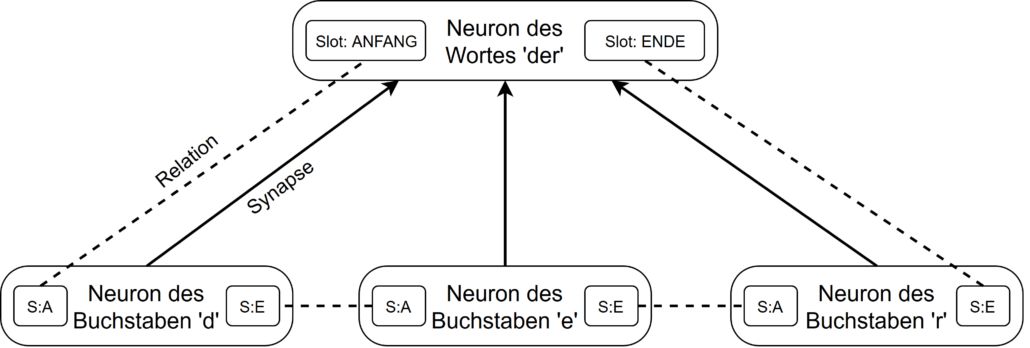
An dieser Stelle möchte ich noch einmal das Beispielneuron für das Wort ‘der’ vom Anfang aufgreifen. Das Wort-Neuron besteht aus drei Eingabesynapsen, die sich jeweils auf die einzelnen Buchstaben des Wortes beziehen. Über die Relationen werden die Eingabesynapsen nun zueinander in eine bestimmte Beziehung gesetzt, so dass das Wort ‘der’ nur erkannt wird, wenn alle Buchstaben in der korrekten Reihenfolge auftreten.
Als Aktivierungsfunktion des Neurons wird hier der im negativen Bereich abgeschnittene (rectified) hyperbolische Tangens verwendet. Dieser hat gerade bei einem UND-verknüpfenden Neuron den Vorteil, dass er selbst bei sehr großen Werten der gewichteten Summe auf den Wert 1 begrenzt ist. Alternativ kann auch die ReLU-Funktion (Rectified Linear Unit) verwendet werden. Diese eignet sich insbesondere für ODER-verknüpfende Neuronen, da sie die Eingabewerte unverzerrt weiterleitet.
Im Gegensatz zu herkömmlichen neuronalen Netzen gibt es hier mehrere Bias Werte, einen für das gesamte Neuron (in diesem Fall auf 5.0 gesetzt) und einen für jede Synapse. Intern werden diese Werte zu einem gemeinsamen Bias aufsummiert. Es ist schon klar, dass dieses Aufteilen des Bias nicht wirklich gut zu Lernregeln wie der Delta-Rule und dem Backpropagation passt, allerdings eignen sich diese Lernverfahren eh nur sehr begrenzt für diese Art von neuronalem Netzwerk. Als Lernverfahren kommen eher von den natürlichen Mechanismen Langzeit-Potenzierung und Langzeit-Depression inspirierte Ansätze in Betracht.

Fazit

Obwohl tiefe neuronale Netze bereits einen langen Weg zurückgelegt haben und mittlerweile beeindruckende Ergebnisse liefern, kann es sich doch lohnen, einen weiteren Blick auf das Original, das menschliche Gehirn und seine Schaltkreise zu werfen. Wenn eine so inhärent komplexe Struktur wie das menschliche Gehirn als Blaupause für ein neuronales Modell verwendet werden soll, müssen vereinfachende Annahmen getroffen werden. Allerdings ist bei diesem Prozess Vorsicht geboten, da sonst wichtige Aspekte des Originals verloren gehen können.

Referenzen

1. Der Aika-Algorithm
   Lukas Molzberger
2. Neuroscience: Exploring the Brain
   Mark F. Bear, Barry W. Connors, Michael A. Paradiso
3. Neural-Symbolic Learning and Reasoning: A Survey and Interpretation
   Tarek R. Besold, Artur d’Avila Garcez, Sebastian Bader; Howard Bowman, Pedro Domingos, Pascal Hitzler, Kai-Uwe Kuehnberger, Luis C. Lamb, ; Daniel Lowd, Priscila Machado Vieira Lima, Leo de Penning, Gadi Pinkas, Hoifung Poon, Gerson Zaverucha
4. Deep Learning: A Critical Appraisal
   Gary Marcus
5. Nonmonotonic Reasoning
   Gerhard Brewka, Ilkka Niemela, Mirosław Truszczynski

About Author

Lukas Molzberger

Lukas Molzberger hat an der Albert-Ludwigs-Universität in Freiburg Informatik mit Schwerpunkt Machine Learning studiert. Er arbeitet derzeit als Senior Software Developer für die meinestadt.de GmbH.

See author's posts