Kurz nach der Jahrtausendwende begann das Zeitalter der digitalen Daten. Seitdem übertrifft die Menge der digitalen Daten die der Analogen [HL11] und dem Maschinellen Lernen stehen enorme Datenmengen zur Verfügung. Unter dem Buzzword „big data“ wird dabei meist nur das reine Volumen gesehen, andere Faktoren, wie die Frequenz mit der die Daten zu verarbeiten sind und die Variabilität der Formate werden oft vernachlässigt, obwohl auch solche Daten unter „big data“ zusammengefasst werden. Betrachtet man das Volumen dann spielen zwei Faktoren eine zentrale Rolle, die das „big“ von „big data“ ausmachen: die Anzahl der Beispieldatensätze und – und dies wird häufig übersehen – die Anzahl der Eigenschaften mit denen die Beispieldaten beschrieben werden.
Wenn von „big data“ gesprochen wird, wird dabei oft angenommen, dass genügend Datensätze vorhanden sind. Für bestimmte Anwendungen jedoch, müssen die Daten in unterschiedliche Gruppen unterschieden werden, um beim Lernen nicht Äpfel und Birnen in einen Topf zu werfen. In solchen Fällen kann es leicht passieren, dass pro Gruppe zu wenig Beispieldaten vorhanden sind und die Frage an Bedeutung gewinnt: „Reichen die Datensätze eigentlich aus, um ein Vorhersagemodel mit einer gewissen Mindestgüte zu lernen?“.
Leider gibt es bisher keine einfache Antwort auf diese Frage, da diese neben der Anzahl der Eigenschaften – der Dimensionalität – der Daten, von der Struktur des Datenraums, der Verteilung der Daten in diesem Raum, dem verwendeten Lernverfahren, der Ausdrucksfähigkeit seiner Hypothesenrepräsentation und seiner endgültigen Parametrisierung abhängt. In der “Computational Learning Theory” wurden jedoch Ansätze zur Abschätzungen von Untergrenzen erarbeitet, die, unter der Annahme idealer Lernverfahren, zu mindestens eine Aussage über die benötigte Mindestmenge an Trainingsdaten gestatten.
Ziel dieses Beitrags ist es auf möglichst anschauliche Art und Weise anhand eines praktischen Beispiels zu zeigen, welchen Einfluss die Dimensionalität der Daten auf die Abschätzung der Anzahl der benötigten Beispiele für das Erlernen von Vorhersagemodellen – genauer einfachen Klassifikationsmodellen[1] – hat und welche Methoden hierfür existieren. In diesem ersten Teil liegt das Hauptaugenmerk auf endlichen Daten- und Hypothesenräumen und wir werden sehen, dass selbst für eine kleine Anzahl von Eigenschaften – sprich Dimensionen – nützliche Aussagen nur für sehr einfache Hypothesenrepräsentationen möglich sind. Im zweiten Teil werden wir einen Abschätzungsansatz betrachten, der die „Unterscheidungsstärke“ unterschiedlicher Lernverfahren berücksichtigt und mit dem auch Abschätzungen für unendliche Daten- und Hypothesenräume möglich werden.
Anwendungsbeispiel
Betrachten wir das Beispiel eines Online-Shops, der Produkte über das Internet verkauft und dessen Produkte klassifiziert werden sollen. Wie die Produkte klassifiziert werden sollen ist für unsere Betrachtungen unerheblich, was wir aber im Kopf haben sollten: der Absatz unterschiedlicher Produkte folgt einer Potenzverteilung. Eine kleine Zahl von Produkten wird sehr häufig verkauft, so dass für sie viele Datensätze existieren (solche Produkte werden gewöhnlicher Weise in konventionellen Geschäften vertrieben, die nur begrenzte Lagerkapazitäten haben). Der Großteil der Produkte wird jedoch eher seltener umgesetzt (auch als „long tail“ bezeichnet), so dass die Anzahl ihrer Datensätze gering ist; u.U. so gering, dass für sie keine verlässlichen Vorhersagemodelle erlernbar sind.
| Zur Illustration gehen wir davon aus, dass in dem Online-Shop Produkte von 500 Marken verkauft werden und diese Produkte neben ihrer Marke durch ihre Größe (10 mögliche Werte), ihre Farbe (20 mögliche Werte), die ersten drei Ebenen der Google Produktkategorien (auf der dritten Ebene 500 mögliche Werte) und ihren Preis (im Bereich 0,49 – 100 €) beschrieben werden. |
In diesem Kontext besitzt die Antwort auf die Frage: „Wie viele Daten werden überhaupt für ein Lernverfahren benötigt?“ offensichtlich konkreten Nutzen,
- da wir abschätzen können, ob für ein konkretes Produkt überhaupt ein sinnvolles Vorhersagemodell erlernbar ist,
- da wir aus der Abschätzung auf die Dauer der Datensammlung schließen können und
- um ggf. die Daten von selten verkauften Produkten inhaltlich oder zeitlich zu aggregieren.
Was uns vorweg klar sein sollte
Die Daten, die wir zum Erlernen von Vorhersagemodellen verwenden, werden durch Eigenschaften (normalerweise als Feature, in der Statistik auch als Variablen bezeichnet) beschrieben. Die Eigenschaften werden in beobachtete und abhängige Eigenschaften (im Maschinellen Lernen auch als Label bezeichnet) unterschieden. Die Wertebereiche der Eigenschaften können in endliche und unendliche Wertebereich unterschieden werden.
Wir können nicht erwarten, dass ein Lernverfahren ein 100%ig korrektes Modell erlernt. Lernverfahren versuchen durch einen induktiven Schluss aus Daten ein Vorhersagemodell zu ermitteln. Da die zur Verfügung stehende Datenmenge immer begrenzt sein wird und die Daten damit realistischer Weise unvollständig sein werden, Messfehler und Inkonsistenzen enthalten können, kann auch ein erlerntes Modell niemals 100%ig korrekt sein.
Viele unterschiedliche Modelle können konsistent mit den verfügbaren Daten sein. Ziel des Lernverfahrens ist es daher mit den verfügbaren Daten das bestmögliche Vorhersagemodell zu ermitteln.
Wir müssen in Kauf nehmen, dass unbekannte, zukünftige oder ungewöhnliche Daten zu fehlerhaften Vorhersagen führen. Zum Lernzeitpunkt ist nur ein Ausschnitt aller Daten verfügbar. Zukünftig erhobene Daten können Veränderungen unterliegen oder es können bisher noch nicht gesehene Fälle auftreten, auf die das erlernte Modell nicht mehr richtig passt.
Aus diesen Fakten ergibt sich die einzig realistische Annahme: ein gutes Lernverfahren soll mit großer Wahrscheinlichkeit eine gute Näherung des richtigen Vorhersagemodells erlernen.
Anzahl benötigter Trainingsfälle
Zur Abschätzung der Anzahl benötigter Trainingsfälle – als Beispielkomplexität (sample complexity) bezeichnet – wurden in der Computational Learning Theory unterschiedliche Ansätze entwickelt. Diese Ansätze beschreiben für idealisierte Lernverfahren unter welchen Bedingungen probabilistisch, approximativ, korrektes Lernen (PAC learning) effizient möglich ist. Grundlegend für die Einsetzbarkeit dieser Ansätze ist die Unterscheidung, ob das Lernen in einem endlichen oder unendlichen Hypothesenraum erfolgt, und ob das Lernverfahren konsistente Hypothesen oder nur näherungsweise Hypothesen, z.B. beim Vorliegen von Messfehlern, zu den Daten erlernen kann.
Endliche Datenräume
Sofern die Daten nur durch nominelle Eigenschaften mit endlichen Wertebereichen beschrieben werden[2], lässt sich die Größe des Datenraums relativ einfach bestimmen. Die folgende Tabelle beschreibt für die wichtigsten nominellen Eigenschaftstypen Größenfaktoren, die im Folgenden zur vereinheitlichten Darstellung verwendet werden:
Type
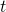 |
Fehlende Werte (NA) ? |
Größe des Wertebereichs
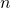 |
Größenfaktor 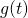 |
| Boolean |
Nein |
2 |
2 |
| Boolean |
Ja |
2 |
3 |
| Nominal (Menge) |
Nein |
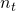 |
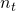 |
| Nominal (Menge) |
Ja |
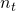 |
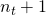 |
Die Größe eines endlichen d-dimensionalen Datenraums 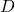 kann allgemein mit folgender Formel bestimmt werden
kann allgemein mit folgender Formel bestimmt werden 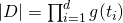 .
.
Das Lernproblem besteht darin: aus einer Teilmenge von Trainingsbeispielen 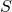 aus dem Datenraum
aus dem Datenraum 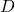 , i.e.
, i.e. 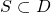 , die ein Trainer dem Lernverfahren vorgibt, um Zielkonzept c zu erlernen, eine Hypothese aus dem Hypothesenraum
, die ein Trainer dem Lernverfahren vorgibt, um Zielkonzept c zu erlernen, eine Hypothese aus dem Hypothesenraum 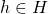 des Lernverfahrens zu ermitteln, welche (möglichst) alle positiven Beispiel
des Lernverfahrens zu ermitteln, welche (möglichst) alle positiven Beispiel 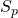 umfasst und (möglichst) alle negativen Beispiele
umfasst und (möglichst) alle negativen Beispiele 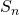 ausschließt.
ausschließt.
Einfache Hypothesenrepräsentation
Die einfachste Hypothesenrepräsentation, in der Lernen, welches über einfaches Erinnern hinausgeht, sinnvoll ist, sind Disjunktionen von Bool’schen Eigenschaften. Eine Beispielanwendung für die diese Repräsentation Sinn macht, ist das Erkennen von Spam-Emails anhand des Vorliegens unterschiedlicher alternativer Eigenschaften, die Spam-Emails charakterisieren. Der Hypothesenraum dieser Sprache besitzt eine Größe von 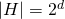 [FoDS18]. Ein Beispiel für ein verbreitetes Lernverfahren, das eine Hypothesenrepräsentation dieses Typs nutzt, ist Naive Bayes.
[FoDS18]. Ein Beispiel für ein verbreitetes Lernverfahren, das eine Hypothesenrepräsentation dieses Typs nutzt, ist Naive Bayes.
Beliebige nominelle Eigenschaften können durch One-Hot- oder Dummy-Encoding als Bool’sche Variablen kodiert werden. Damit ergibt sich zum Erlernen von Disjunktionen kodierter, Bool’scher Eigenschaften die Größe des Hypothesenraums als 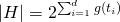 .
.
Um unser Produktbeispiel in dieser Sprache zu repräsentieren, müssen die Eigenschaften geeignet kodiert werden, z.B. durch One-Hot- oder Dummy-Encoding, bei dem jeder Wert einer Eigenschaft durch eine neue bool’sche Variable kodiert wird. Hieraus ergeben sich im Fall von One-Hot-Encoding 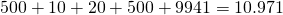 und im Fall von Dummy-Encoding und im Fall von Dummy-Encoding 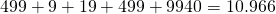 neue Bool’sche Eigenschaften. neue Bool’sche Eigenschaften. |
Eigenschaftsvektoren (Feature-Vektoren, bzw. Konjunktionen von Eigenschaften) stellen die nächstkomplexere Repräsentationssprache dar, die, solange sie nicht um ein Konstrukt zur Verallgemeinerung erweitert wird, sehr unspektakulär ist, da Beispiele mit ihr lediglich erinnert werden. Erst wenn ein „don’t care“-Symbol, wie z.B. „?“, für beliebige Eigenschaftswerte hinzugefügt wird, wird die extremste Form von Generalisierung möglich, die von einzelnen Werten gleich auf alle Werte generalisiert [ML97]. Durch das „don’t care“-Symbol wird der Größenfaktor g um einen weiteren Wert erhöht. Für diese Repräsentation beträgt die Größe des Hypothesenraums über rein bool‘schen Eigenschaften (inkl. „don’t care“) 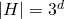 und für allgemeine endliche Eigenschaften
und für allgemeine endliche Eigenschaften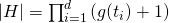 . Diese Repräsentation ist sehr eingeschränkt und erlaubt es nur einzelne und keine kombinierten Konzepte zu erlernen. Sie ist daher eigentlich nur von theoretischem Interesse und wird – soweit bekannt – in keinem praktisch eingesetzten Lernverfahren genutzt.
. Diese Repräsentation ist sehr eingeschränkt und erlaubt es nur einzelne und keine kombinierten Konzepte zu erlernen. Sie ist daher eigentlich nur von theoretischem Interesse und wird – soweit bekannt – in keinem praktisch eingesetzten Lernverfahren genutzt.
Interessanter ist eine Verallgemeinerung dieser Repräsentationssprache, die k-CNF (konjunktive Normalform), die aus einer Konjunktion von Disjunktionen der Länge k besteht, die sowohl polynomielle Beispiel- als auch Zeitkomplexität besitzt [ML97] und für die ein effizienter Algorithmus existiert. Diese Repräsentation lässt sich auch auf einen d-dimensionalen Eigenschaftsvektor übertragen, in dem für jede Eigenschaft Generalisierungen über beliebige Teilmengen erlaubt werden. Die Größe des Hypothesenraums dieser Sprache beträgt 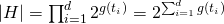 . Mit dieser Sprache können alle Eigenschaften zwar separat auf beliebige Teilmengen generalisiert werden, Korrelationen zwischen Eigenschaften werden jedoch nicht berücksichtigt.
. Mit dieser Sprache können alle Eigenschaften zwar separat auf beliebige Teilmengen generalisiert werden, Korrelationen zwischen Eigenschaften werden jedoch nicht berücksichtigt.
Für Repräsentationssprachen, die keinerlei Einschränkungen machen, besitzt der Hypothesenraum für Daten mit d bool‘schen Eigenschaften eine Größe von 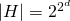 . Auf beliebige endliche Eigenschaften übertragen, kann diese Aussage zu
. Auf beliebige endliche Eigenschaften übertragen, kann diese Aussage zu 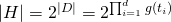 verallgemeinert werden.
verallgemeinert werden.
Wie aus diesen Abschätzungen ersichtlich wird, hat die Dimensionalität d der Daten einen direkten Einfluss auf die Größe des Hypothesenraums und damit auf die Anzahl der von einem Lernverfahren zu berücksichtigenden Konzepte.
Realistische Hypothesenrepräsentation
Bis auf einfache Disjunktionen bool’scher Eigenschaften, sind einfache Hypothesenrepräsentationen entweder zu ausdrucksschwach, so dass nützliche Konzepte kaum ausdrückbar sind, oder zu ausdrucksstark, so dass Lernen in vertretbarer nicht-exponentieller Zeit nicht möglich ist. Die gängigen Lernverfahren, wie k-Nearest Neighbors, Naive Bayes, Decision Trees, Random Forrests, AdaBoost, XGBoost, Logistic Regression, Support Vector Machines und Neuronale Netze, etc. beschränken durch spezifische Annahmen (inductive bias) den Hypothesenraum, um so nützliche Konzepte in vernünftiger Zeit zu erlernen.
Leider lassen sich nur für wenige der real eingesetzten Verfahren Abschätzungen für die Größe des Hypothesenraums finden.
| Verfahren |
|H| |
Parameter |
| Boolean-coded Naive Bayes |
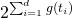 |
|
| Boolean-coded Decision Trees[3] |
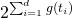 |
|
| Boolean-coded Decision Trees with limited depth [4] |
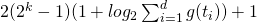 |
k = Tiefenbegrenzung |
Lernen eines zu allen Trainingsdaten konsistenten Konzepts (aka Overfitting)
Unter der Annahme eines idealen Lernalgorithmus, kann die Größe des Hypothesenraums dazu verwendet werden die Anzahl der Trainingsdaten 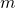 die ein „konsistenter Lernalgorithmus“[5] benötigt, um ein beliebiges Konzept mit einem maximalen Fehler
die ein „konsistenter Lernalgorithmus“[5] benötigt, um ein beliebiges Konzept mit einem maximalen Fehler  und einer Unsicherheit
und einer Unsicherheit  (bzw. einer Wahrscheinlichkeit von
(bzw. einer Wahrscheinlichkeit von  ) zu erlernen, abgeschätzt werden mit[6]
) zu erlernen, abgeschätzt werden mit[6]
![Rendered by QuickLaTeX.com \[m \geq \frac{1}{\epsilon}(ln{(|H|)} + ln{(\frac{1}{\delta})})\]](https://data-science-blog.com/de/wp-content/ql-cache/quicklatex.com-901f897bb0040e542c0eeaa14098b677_l3.png)
Ein, dieser Abschätzung zugrundeliegender, idealer Lernalgorithmus, ist jedoch für praktische Anwendungen unrealistisch, da er zwar für die Trainingsdaten ein konsistentes Konzept ermitteln würde, welches aber bei unbekannten, neuen Daten versagen kann. Der angenommene Lernalgorithmus unterliegt der „Überanpassung“ (overfitting).
Nichts desto trotz ist diese Abschätzungsformel hilfreich, da sie eine Aussage erlaubt, wie viele Trainingsbeispiele im besten Fall ausreichen, um mit einem idealen Lernverfahren ein Konzept mit einem maximalen Fehler von  und einer Unsicherheit von höchstens
und einer Unsicherheit von höchstens  zu erlernen, das in der genutzten Hypothesenrepräsentation ausdrückbar ist.
zu erlernen, das in der genutzten Hypothesenrepräsentation ausdrückbar ist.
Agnostisches Lernen eines Konzeptes, das möglichst gut zu den Trainingsdaten passt
Überanpassung wollen wir in der Regel vermeiden, damit die erlernten Vorhersagemodelle auch auf unbekannte, fehlerbehaftete oder teilweise inkonsistente Daten anwendbar sind. Anders ausgedrückt: das zu erlernende Konzept  kann etwas außerhalb des Hypothesenraums liegen, der durch das eingesetzte Lernverfahren erfasst wird. Dies bedeutet, dass wir im Hypothesenraum des Lernverfahrens nur eine Näherung
kann etwas außerhalb des Hypothesenraums liegen, der durch das eingesetzte Lernverfahren erfasst wird. Dies bedeutet, dass wir im Hypothesenraum des Lernverfahrens nur eine Näherung 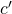 erlernen können, die möglichst gut sein sollte. Solch ein – als agnostisch bezeichnetes – Lernverfahren muss daher bestrebt sein den Fehler zwischen den Trainingsdaten und dem Fehler der sich durch das Erlernen der Näherung
erlernen können, die möglichst gut sein sollte. Solch ein – als agnostisch bezeichnetes – Lernverfahren muss daher bestrebt sein den Fehler zwischen den Trainingsdaten und dem Fehler der sich durch das Erlernen der Näherung 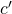 ergibt möglichst klein zu halten.
ergibt möglichst klein zu halten.
Auch hierfür kann, unter der Annahme eines idealen Lernalgorithmus, die Größe des Hypothesenraums dazu verwendet werden die Anzahl der Trainingsdaten 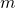 die ein „agnostisches Lernverfahren“ benötigt, um eine gute Näherung an das zu erlernende Konzept in einem endlichen Hypothesenraum mit einem maximalen Fehler
die ein „agnostisches Lernverfahren“ benötigt, um eine gute Näherung an das zu erlernende Konzept in einem endlichen Hypothesenraum mit einem maximalen Fehler  und einer Unsicherheit
und einer Unsicherheit  (bzw. einer Wahrscheinlichkeit von
(bzw. einer Wahrscheinlichkeit von  ) zu erlernen, abgeschätzt werden mit[6]
) zu erlernen, abgeschätzt werden mit[6]
![Rendered by QuickLaTeX.com \[m \geq \frac{1}{2\epsilon^2}(ln{(|H|)} + ln{(\frac{2}{\delta})})\]](https://data-science-blog.com/de/wp-content/ql-cache/quicklatex.com-0630d9d4a9a075de904ef5d5610c93eb_l3.png)
| Auf das Beispiel angewendet müsste sich – unter der Annahme gleicher Rahmenbedingungen – die Mindestzahl von Trainingsbeispielen auf m = 490 belaufen. D.h. die Daten von Produkt A könnten zum Lernen der Klassifikation verwendet werden, die Datenmenge für Produkt B wäre jedoch nicht ausreichend. |
Folgerung
Mit diesem ersten Beitrag haben wir anhand eines kleinen realen Beispiels gezeigt, wie sich für einen idealen Lernalgorithmus über die Betrachtung der Größe endlicher Hypothesenräume, die Mindestanzahl der benötigten Trainingsbeispiel abschätzen lässt.
Auch wenn es sich hierbei um eine idealisierte Betrachtung handelt, erlauben solche Abschätzungen Aussagen darüber, wann Lernverfahren nur mit einem größeren Fehler behaftet einsetzbar sind.
Diese Betrachtung erstreckte sich bisher nur über endliche Eigenschaften und berücksichtigt die Komplexität der Hypothesenrepräsentation – eine der wesentlichen Eigenschaften eines Lernverfahrens – noch nicht. Dies wird Thema des zweiten Teils sein, in dem wir sehen werden, wie sich Abschätzung auf der Basis der – sogenannten – Vapnik-Chervonenkis-Dimension (VC-Dimension) für viele gängige Klassen von Lernverfahren einsetzen lassen.
Fußnoten
[1] Wir betrachten hierbei nur rein binäre, binomiale resp. Bool’sche Klassifikationsprobleme, deren Aussagen sich jedoch auch auf multinomiale Klassifikation und reell-wertige Vorhersagemodelle übertragen lassen (siehe [ESL09], Seite 238).
[2] Unendlich, überabzählbare Eigenschaften lassen sich in Abhängigkeit vom Anwendungsproblem und der erforderlichen Genauigkeit oft diskretisieren und als ordinale Daten oder Intervalle ganzer Zahlen repräsentieren, wie z.B. Alter, Körpergröße, Längen, Temperatur, und Zeitintervalle usw., wenn es ausreichend ist diese mit einer Genauigkeit von Jahren, cm, mm, Zehntelgrad oder Sekunden zu erfassen.
[3] Vollausgebaute Decision Trees unterliegen der Gefahr der „Überanpassung“ (overfitting) und werden in der Regel gestutzt, um dies zu vermeiden. Die Abschätzung stellt daher die Obergrenze dar.
[4] http://www.cs.cmu.edu/~guestrin/Class/10701/slides/learningtheory-bigpicture.pdf und https://www.autonlab.org/_media/tutorials/pac05.pdf (Letzter Zugriff: 10.3.2018)
[5] Ein „konsistenter Lernalgorithmus“ erlernt Hypothesen, die – wann immer möglich – perfekt zu den Trainingsdaten passen [ML97].
[6] Details zur Ableitung der beschriebenen Untergrenzen finden sich u.a. in [ML97], [FoML12] oder [FoDS18].
Referenzen
[HL11] „The World’s Technological Capacity to Store, Communicate, and Compute Information“, M. Hilbert, P. López, Science 332, 60, 2011, http://www.uvm.edu/pdodds/files/papers/others/2011/hilbert2011a.pdf (letzter Zugriff: 14. März 2018)
[ESL09] “The Elements of Statistical Learning”, T. Hastie, R. Tibshirani, J. Friedman, 2nd Edition, Springer, 2009.
[ML97] „Machine Learning“, T. Mitchell, McGraw-Hill, 1997.
[FoML12] „Foundations of Machine Learning“, M. Mohri, A. Rostamizadeh, A. Talwalkar, The MIT Press, 2012.
[FoDS18] „Foundations of Data Science“, A. Blum, J. Hopcroft, R. Kannan, Cornell University, https://www.cs.cornell.edu/jeh/book.pdf, Jan. 4th, 2018 (letzter Zugriff: 14. März 2018)
 Der Einsatz von Künstlicher Intelligenz zur Auswertung von Geschäfts- oder Maschinendaten ist auch das Leit-Thema der zweitägigen Data Leader Days 2018 in Berlin. Am 14. November 2018 sprechen renommierte Data Leader über Anwendungsfälle, Erfolge und Chancen mit Geschäfts- und Finanzdaten. Der 15. November 2018 konzentriert sich auf Automotive- und Maschinendaten mit hochrangigen Anwendern aus der produzierenden Industrie und der Automobilzuliefererindustrie. Seien Sie dabei und nutzen Sie die Chance, sich mit führenden KI-Anwendern auszutauschen.
Der Einsatz von Künstlicher Intelligenz zur Auswertung von Geschäfts- oder Maschinendaten ist auch das Leit-Thema der zweitägigen Data Leader Days 2018 in Berlin. Am 14. November 2018 sprechen renommierte Data Leader über Anwendungsfälle, Erfolge und Chancen mit Geschäfts- und Finanzdaten. Der 15. November 2018 konzentriert sich auf Automotive- und Maschinendaten mit hochrangigen Anwendern aus der produzierenden Industrie und der Automobilzuliefererindustrie. Seien Sie dabei und nutzen Sie die Chance, sich mit führenden KI-Anwendern auszutauschen.

 Prof. Dr. Klaus Jung studierte Physik an der TU Berlin, wo er im Bereich der Mathematischen Physik promovierte. Bis 2008 arbeitete er als Leiter F&E bei der Firma LuraTech im Bereich der Dokumentenverarbeitung und Langzeitarchivierung. In der JPEG-Gruppe leitete er die deutsche Delegation bei der Standardisierung von JPEG2000. Seit 2008 ist er Professor für Medieninformatik an der HTW Berlin mit dem Schwerpunkt „Visual Computing“.
Prof. Dr. Klaus Jung studierte Physik an der TU Berlin, wo er im Bereich der Mathematischen Physik promovierte. Bis 2008 arbeitete er als Leiter F&E bei der Firma LuraTech im Bereich der Dokumentenverarbeitung und Langzeitarchivierung. In der JPEG-Gruppe leitete er die deutsche Delegation bei der Standardisierung von JPEG2000. Seit 2008 ist er Professor für Medieninformatik an der HTW Berlin mit dem Schwerpunkt „Visual Computing“.



 Alice Albrecht ist Research Engineer bei
Alice Albrecht ist Research Engineer bei 
 Andreas Festl ist Data Scientist bei VIRTUAL VEHICLE, ein führendes F&E Zentrum für die Automobil- und Bahnindustrie mit Sitz in Graz, Österreich. Das Zentrum konzentriert sich auf die konsequente Virtualisierung der Fahrzeugentwicklung. Wesentliches Element dabei ist die Verknüpfung von numerischer Simulation und Hardware-Testen, welche ein umfassendes HW-SW Systemdesign sicherstellt. Herr Festl forscht dort an Kontext-basierten Informationssystemen für den Einsatz im Fahrzeug und in der Entwicklung. Er ist ausgebildeter Mathematiker, der sich schon früh dem Thema Data Science verschrieben hat. Zusätzlich ist Herr Festl in der Lehre für Data and Information Science an der Fachhochschule Joanneum tätig.
Andreas Festl ist Data Scientist bei VIRTUAL VEHICLE, ein führendes F&E Zentrum für die Automobil- und Bahnindustrie mit Sitz in Graz, Österreich. Das Zentrum konzentriert sich auf die konsequente Virtualisierung der Fahrzeugentwicklung. Wesentliches Element dabei ist die Verknüpfung von numerischer Simulation und Hardware-Testen, welche ein umfassendes HW-SW Systemdesign sicherstellt. Herr Festl forscht dort an Kontext-basierten Informationssystemen für den Einsatz im Fahrzeug und in der Entwicklung. Er ist ausgebildeter Mathematiker, der sich schon früh dem Thema Data Science verschrieben hat. Zusätzlich ist Herr Festl in der Lehre für Data and Information Science an der Fachhochschule Joanneum tätig.