Machine Learning Archives

Tag Archive for: Machine Learning

Die führende Fachkonferenz für Machine Learning

October 15, 2020/in Data Science News, Recommendations/by events

Seien Sie dabei, wenn sich am 16. bis 17. November 2020 Anwender, Entscheider und Experten von Predictive Analytics und Machine Learning virtual treffen, um sich über die neuesten Erkenntnisse und Fortschritte zu informieren.

Vom Data Lab zu Data Ops

Die Zeit des Experimentierens ist vorbei. Unternehmen erwarten, dass ihre Data Labs das liefern, was ihnen der KI-Hype versprochen hat: mehr Kunden, höhere Umsätze, effizientere Prozesse und vieles mehr. Doch viele Projekte stecken in der PoC-Falle fest: sie funktionieren als Prototyp – aber nicht im realen Betrieb. Aus der Data Science muss eine Data Industry werden: wir müssen selbst lernen, effizienter und effektiver zu werden – und zwar darin die wirklich kritischen Herausforderungen im Unternehmen zu identifizieren, die passenden Lösungsideen zu entwickeln, die Ideen schnell in funktionierende Modelle zu übersetzen, aus den Modellen skalierbare Lösungen zu entwickeln und schließlich dafür zu sorgen, dass diese Lösungen von den Fachbereichen gewinnbringend genutzt werden. Dies verlangt ein neues Selbstverständnis: wir sind nicht das Experimentierlabor der Unternehmen – sondern deren Maschinenraum: Data Ops statt Data Labs.

Predictive Analytics für die Finanz- & Versicherungsbranche

Auf der diesjährigen Konferenz starten wir ein neues Format: eine Vortragsreihe für angewandte Predictive Analytics in der Finanz- und Versicherungsbranche. Dieser eintägige Track zeigt Ihnen die wichtigsten Anwendungsfälle von Machine & Deep Learning für Banken, Versicherungen, Investoren und Fonds auf, indem er Ihnen reale Projekte von bekannten Unternehmen vorstellt. Sie erfahren, wie Sie Datenschutz- und Regulierungsprobleme lösen, Ihre Datenbestände mit Data Governance und Datenstrategie verwalten und verwerten sowie mit Data Science & Analytics erfolgreiche Datenprodukte entwickeln und betreiben.

Lassen Sie sich wertvolle Tipps und Tricks von erfahrenen Experten aus namhaften Unternehmen nicht entgehen!

Mit dem Code “DATASCIENCEPAW” bekommen Sie zusätzliche 15 Prozent Rabatt auf Ihre Buchung.

Interview: Data Science in der Finanzbranche

July 29, 2020/in Data Science, Insights, Interviews, Main Category/by Benjamin Aunkofer

Interview mit Torsten Nahm von der DKB (Deutsche Kreditbank AG) über Data Science in der Finanzbranche

Torsten Nahm ist Head of Data Science bei der DKB (Deutsche Kreditbank AG) in Berlin. Er hat Mathematik in Bonn mit einem Schwerpunkt auf Statistik und numerischen Methoden studiert. Er war zuvor u.a. als Berater bei KPMG und OliverWyman tätig sowie bei dem FinTech Funding Circle, wo er das Risikomanagement für die kontinentaleuropäischen Märkte geleitet hat.

Hallo Torsten, wie bist du zu deinem aktuellen Job bei der DKB gekommen?

Die Themen Künstliche Intelligenz und maschinelles Lernen haben mich schon immer fasziniert. Den Begriff „Data Science“ gibt es ja noch gar nicht so lange. In meinem Studium hieß das „statistisches Lernen“, aber im Grunde ging es um das gleiche Thema: dass ein Algorithmus Muster in den Daten erkennt und dann selbstständig Entscheidungen treffen kann.

Im Rahmen meiner Tätigkeit als Berater für verschiedene Unternehmen und Banken ist mir klargeworden, an wie vielen Stellen man mit smarten Algorithmen ansetzen kann, um Prozesse und Produkte zu verbessern, Risiken zu reduzieren und das Kundenerlebnis zu verbessern. Als die DKB jemanden gesucht hat, um dort den Bereich Data Science weiterzuentwickeln, fand ich das eine äußerst spannende Gelegenheit. Die DKB bietet mit über 4 Millionen Kunden und einem auf Nachhaltigkeit fokussierten Geschäftsmodell m.E. ideale Möglichkeiten für anspruchsvolle aber auch verantwortungsvolle Data Science.

Du hast viel Erfahrung in Data Science und im Risk Management sowohl in der Banken- als auch in der Versicherungsbranche. Welche Rolle siehst du für Big Data Analytics in der Finanz- und Versicherungsbranche?

Banken und Versicherungen waren mit die ersten Branchen, die im großen Stil Computer eingesetzt haben. Das ist einfach ein unglaublich datengetriebenes Geschäft. Entsprechend haben komplexe Analysemethoden und auch Big Data von Anfang an eine große Rolle gespielt – und die Bedeutung nimmt immer weiter zu. Technologie hilft aber vor allem dabei Prozesse und Produkte für die Kundinnen und Kunden zu vereinfachen und Banking als ein intuitives, smartes Erlebnis zu gestalten – Stichwort „Die Bank in der Hosentasche“. Hier setzen wir auf einen starken Kundenfokus und wollen die kommenden Jahre als Bank deutlich wachsen.

Kommen die Bestrebungen hin zur Digitalisierung und Nutzung von Big Data gerade eher von oben aus dem Vorstand oder aus der Unternehmensmitte, also aus den Fachbereichen, heraus?

Das ergänzt sich idealerweise. Unser Vorstand hat sich einer starken Wachstumsstrategie verschrieben, die auf Automatisierung und datengetriebenen Prozessen beruht. Gleichzeitig sind wir in Dialog mit vielen Bereichen der Bank, die uns fragen, wie sie ihre Produkte und Prozesse intelligenter und persönlicher gestalten können.

Was ist organisatorische Best Practice? Finden die Analysen nur in deiner Abteilung statt oder auch in den Fachbereichen?

Ich bin ein starker Verfechter eines „Hub-and-Spoke“-Modells, d.h. eines starken zentralen Bereichs zusammen mit dezentralen Data-Science-Teams in den einzelnen Fachbereichen. Wir als zentraler Bereich erschließen dabei neue Technologien (wie z.B. die Cloud-Nutzung oder NLP-Modelle) und arbeiten dabei eng mit den dezentralen Teams zusammen. Diese wiederum haben den Vorteil, dass sie direkt an den jeweiligen Kollegen, Daten und Anwendern dran sind.

Wie kann man sich die Arbeit bei euch in den Projekten vorstellen? Was für Profile – neben dem Data Scientist – sind beteiligt?

Inzwischen hat im Bereich der Data Science eine deutliche Spezialisierung stattgefunden. Wir unterscheiden grob zwischen Machine Learning Scientists, Data Engineers und Data Analysts. Die ML Scientists bauen die eigentlichen Modelle, die Date Engineers führen die Daten zusammen und bereiten diese auf und die Data Analysts untersuchen z.B. Trends, Auffälligkeiten oder gehen Fehlern in den Modellen auf den Grund. Dazu kommen noch unsere DevOps Engineers, die die Modelle in die Produktion überführen und dort betreuen. Und natürlich haben wir in jedem Projekt noch die fachlichen Stakeholder, die mit uns die Projektziele festlegen und von fachlicher Seite unterstützen.

Und zur technischen Organisation, setzt ihr auf On-Premise oder auf Cloud-Lösungen?

Unsere komplette Data-Science-Arbeitsumgebung liegt in der Cloud. Das vereinfacht die gemeinsame Arbeit enorm, da wir auch sehr große Datenmengen z.B. direkt über S3 gemeinsam bearbeiten können. Und natürlich profitieren wir auch von der großen Flexibilität der Cloud. Wir müssen also z.B. kein Spark-Cluster oder leistungsfähige Multi-GPU-Instanzen on premise vorhalten, sondern nutzen und zahlen sie nur, wenn wir sie brauchen.

Gibt es Stand heute bereits Big Data Projekte, die die Prototypenphase hinter sich gelassen haben und nun produktiv umgesetzt werden?

Ja, wir haben bereits mehrere Produkte, die die Proof-of-Concept-Phase erfolgreich hinter sich gelassen haben und nun in die Produktion umgesetzt werden. U.a. geht es dabei um die Automatisierung von Backend-Prozessen auf Basis einer automatischen Dokumentenerfassung und -interpretation, die Erkennung von Kundenanliegen und die Vorhersage von Prozesszeiten.

In wie weit werden unstrukturierte Daten in die Analysen einbezogen?

Das hängt ganz vom jeweiligen Produkt ab. Tatsächlich spielen in den meisten unserer Projekte unstrukturierte Daten eine große Rolle. Das macht die Themen natürlich anspruchsvoll aber auch besonders spannend. Hier ist dann oft Deep Learning die Methode der Wahl.

Wie stark setzt ihr auf externe Vendors? Und wie viel baut ihr selbst?

Wenn wir ein neues Projekt starten, schauen wir uns immer an, was für Lösungen dafür schon existieren. Bei vielen Themen gibt es gute etablierte Lösungen und Standardtechnologien – man muss nur an OCR denken. Kommerzielle Tools haben wir aber im Ergebnis noch fast gar nicht eingesetzt. In vielen Bereichen ist das Open-Source-Ökosystem am weitesten fortgeschritten. Gerade bei NLP zum Beispiel entwickelt sich der Forschungsstand rasend. Die besten Modelle werden dann von Facebook, Google etc. kostenlos veröffentlicht (z.B. BERT und Konsorten), und die Vendors von kommerziellen Lösungen sind da Jahre hinter dem Stand der Technik.

Letzte Frage: Wie hat sich die Coronakrise auf deine Tätigkeit ausgewirkt?

In der täglichen Arbeit eigentlich fast gar nicht. Alle unsere Daten sind ja per Voraussetzung digital verfügbar und unsere Cloudumgebung genauso gut aus dem Home-Office nutzbar. Aber das Brainstorming, gerade bei komplexen Fragestellungen des Feature Engineering und Modellarchitekturen, finde ich per Videocall dann doch deutlich zäher als vor Ort am Whiteboard. Insofern sind wir froh, dass wir uns inzwischen auch wieder selektiv in unseren Büros treffen können. Insgesamt hat die DKB aber schon vor Corona auf unternehmensweites Flexwork gesetzt und bietet dadurch per se flexible Arbeitsumgebungen über die IT-Bereiche hinaus.

Data Science für Smart Home im familiengeführten Unternehmen Miele

June 30, 2020/in Artificial Intelligence, Data Science, Insights, Interviews, Machine Learning, Main Category, Use Cases/by Benjamin Aunkofer

Dr. Florian Nielsen ist Principal for AI und Data Science bei Miele im Bereich Smart Home und zuständig für die Entwicklung daten-getriebener digitaler Produkte und Produkterweiterungen. Der studierte Informatiker promovierte an der Universität Ulm zum Thema multimodale kognitive technische Systeme.

Data Science Blog: Herr Dr. Nielsen, viele Unternehmen und Anwender reden heute schon von Smart Home, haben jedoch eher ein Remote Home. Wie machen Sie daraus tatsächlich ein Smart Home?

Tatsächlich entspricht das auch meiner Wahrnehmung. Die bloße Steuerung vernetzter Produkte über digitale Endgeräte macht aus einem vernetzten Produkt nicht gleich ein „smartes“. Allerdings ist diese Remotefunktion ein notwendiges Puzzlestück in der Entwicklung von einem nicht vernetzten Produkt, über ein intelligentes, vernetztes Produkt hin zu einem Ökosystem von sich ergänzenden smarten Produkten und Services. Vernetzte Produkte, selbst wenn sie nur aus der Ferne gesteuert werden können, erzeugen Daten und ermöglichen uns die Personalisierung, Optimierung oder gar Automatisierung von Produktfunktionen basierend auf diesen Daten voran zu treiben. „Smart“ wird für mich ein Produkt, wenn es sich beispielsweise besser den Bedürfnissen des Nutzers anpasst oder über Assistenzfunktionen eine Arbeitserleichterung im Alltag bietet.

Data Science Blog: Smart Home wiederum ist ein großer Begriff, der weit mehr als Geräte für Küchen und Badezimmer betrifft. Wie weit werden Sie hier ins Smart Home vordringen können?

Smart Home ist für mich schon fast ein verbrannter Begriff. Der Nutzer assoziiert hiermit doch vor allem die Steuerung von Heizung und Rollladen. Im Prinzip geht es doch um eine Vision in der sich smarte, vernetzte Produkt in ein kontextbasiertes Ökosystem einbetten um den jeweiligen Nutzer in seinem Alltag, nicht nur in seinem Zuhause, Mehrwert mit intelligenten Produkten und Services zu bieten. Für uns fängt das beispielsweise nicht erst beim Starten des Kochprozesses mit Miele-Geräten an, sondern deckt potenziell die komplette „User Journey“ rund um Ernährung (z. B. Inspiration, Einkaufen, Vorratshaltung) und Kochen ab. Natürlich überlegen wir verstärkt, wie Produkte und Services unser existierendes Produktportfolio ergänzen bzw. dem Nutzer zugänglicher machen könnten, beschränken uns aber hierauf nicht. Ein zusätzlicher für uns als Miele essenzieller Aspekt ist allerdings auch die Privatsphäre des Kunden. Bei der Bewertung potenzieller Use-Cases spielt die Privatsphäre unserer Kunden immer eine wichtige Rolle.

Data Science Blog: Die meisten Data-Science-Abteilungen befassen sich eher mit Prozessen, z. B. der Qualitätsüberwachung oder Prozessoptimierung in der Produktion. Sie jedoch nutzen Data Science als Komponente für Produkte. Was gibt es dabei zu beachten?

Kundenbedürfnisse. Wir glauben an nutzerorientierte Produktentwicklung und dementsprechend fängt alles bei uns bei der Identifikation von Bedürfnissen und potenziellen Lösungen hierfür an. Meist starten wir mit „Design Thinking“ um die Themen zu identifizieren, die für den Kunden einen echten Mehrwert bieten. Wenn dann noch Data Science Teil der abgeleiteten Lösung ist, kommen wir verstärkt ins Spiel. Eine wesentliche Herausforderung ist, dass wir oft nicht auf der grünen Wiese starten können. Zumindest wenn es um ein zusätzliches Produktfeature geht, das mit bestehender Gerätehardware, Vernetzungsarchitektur und der daraus resultierenden Datengrundlage zurechtkommen muss. Zwar sind unsere neuen Produktgenerationen „Remote Update“-fähig, aber auch das hilft uns manchmal nur bedingt. Dementsprechend ist die Antizipation von Geräteanforderungen essenziell. Etwas besser sieht es natürlich bei Umsetzungen von cloud-basierten Use-Cases aus.

Data Science Blog: Es heißt häufig, dass Data Scientists kaum zu finden sind. Ist Recruiting für Sie tatsächlich noch ein Thema?

Data Scientists, hier mal nicht interpretiert als Mythos „Unicorn“ oder „Full-Stack“ sind natürlich wichtig, und auch nicht leicht zu bekommen in einer Region wie Gütersloh. Aber Engineers, egal ob Data, ML, Cloud oder Software generell, sind der viel wesentlichere Baustein für uns. Für die Umsetzung von Ideen braucht es nun mal viel Engineering. Es ist mittlerweile hinlänglich bekannt, dass Data Science einen zwar sehr wichtigen, aber auch kleineren Teil des daten-getriebenen Produkts ausmacht. Mal abgesehen davon habe ich den Eindruck, dass immer mehr „Data Science“- Studiengänge aufgesetzt werden, die uns einerseits die Suche nach Personal erleichtern und andererseits ermöglichen Fachkräfte einzustellen die nicht, wie früher einen PhD haben (müssen).

Data Science Blog: Sie haben bereits einige Analysen erfolgreich in Ihre Produkte integriert. Welche Herausforderungen mussten dabei überwunden werden? Und welche haben Sie heute noch vor sich?

Wir sind, wie viele Data-Science-Abteilungen, noch ein relativ junger Bereich. Bei den meisten unserer smarten Produkte und Services stecken wir momentan in der MVP-Entwicklung, deshalb gibt es einige Herausforderungen, die wir aktuell hautnah erfahren. Dies fängt, wie oben erwähnt, bei der Berücksichtigung von bereits vorhandenen Gerätevoraussetzungen an, geht über mitunter heterogene, inkonsistente Datengrundlagen, bis hin zur Etablierung von Data-Science- Infrastruktur und Deploymentprozessen. Aus meiner Sicht stehen zudem viele Unternehmen vor der Herausforderung die Weiterentwicklung und den Betrieb von AI bzw. Data- Science- Produkten sicherzustellen. Verglichen mit einem „fire-and-forget“ Mindset nach Start der Serienproduktion früherer Zeiten muss ein Umdenken stattfinden. Daten-getriebene Produkte und Services „leben“ und müssen dementsprechend anders behandelt und umsorgt werden – mit mehr Aufwand aber auch mit der Chance „immer besser“ zu werden. Deshalb werden wir Buzzwords wie „MLOps“ vermehrt in den üblichen Beraterlektüren finden, wenn es um die nachhaltige Generierung von Mehrwert von AI und Data Science für Unternehmen geht. Und das zu Recht.

Data Science Blog: Data Driven Thinking wird heute sowohl von Mitarbeitern in den Fachbereichen als auch vom Management verlangt. Gerade für ein Traditionsunternehmen wie Miele sicherlich eine Herausforderung. Wie könnten Sie diese Denkweise im Unternehmen fördern?

Data Driven Thinking kann nur etabliert werden, wenn überhaupt der Zugriff auf Daten und darauf aufbauende Analysen gegeben ist. Deshalb ist Daten-Demokratisierung der wichtigste erste Schritt. Aus meiner Perspektive geht es darum initial die Potenziale aufzuzeigen, um dann mithilfe von Daten Unsicherheiten zu reduzieren. Wir haben die Erfahrung gemacht, dass viele Fachbereiche echtes Interesse an einer daten-getriebenen Analyse ihrer Hypothesen haben und dankbar für eine daten-getriebene Unterstützung sind. Miele war und ist ein sehr innovatives Unternehmen, dass „immer besser“ werden will. Deshalb erfahren wir momentan große Unterstützung von ganz oben und sind sehr positiv gestimmt. Wir denken, dass ein Schritt in die richtige Richtung bereits getan ist und mit zunehmender Zahl an Multiplikatoren ein „Data Driven Thinking“ sich im gesamten Unternehmen etablieren kann.

CAPTCHAs lösen via Maschine Learning

March 9, 2020/in Artificial Intelligence, Data Science, Deep Learning, Insights, Machine Learning, Main Category/by Pavel Shipilov

Wie weit ist das maschinelle Lernen auf dem Gebiet der CAPTCHA-Lösung fortgeschritten?

Maschinelles Lernen ist mehr als ein Buzzword, denn unter der Haube stecken viele Algorithemen, die eine ganze Reihe von Problemen lösen können. Die Lösung von CAPTCHA ist dabei nur eine von vielen Aufgaben, die Machine Learning bewältigen kann. Durch die Arbeit an ein paar Problemen im Zusammenhang mit dem konvolutionellen neuronalen Netz haben wir festgestellt, dass es in diesem Bereich noch viel Verbesserungspotenzial gibt. Die Genauigkeit der Erkennung ist oftmals noch nicht gut genug. Schauen wir uns im Einzelnen an, welche Dienste wir haben, um dieses Problem anzugehen, und welche sich dabei als die besten erweisen.

Was ist CAPTCHA?

CAPTCHA ist kein fremder Begriff mehr für Web-Benutzer. Es handelt sich um die ärgerliche menschliche Validierungsprüfung, die auf vielen Websites hinzugefügt wird. Es ist ein Akronym für Completely Automated Public Turing test for tell Computer and Humans Apart. CAPTCHA kann als ein Computerprogramm bezeichnet werden, das dazu entwickelt wurde, Mensch und Maschine zu unterscheiden, um jede Art von illegaler Aktivität auf Websites zu verhindern. Der Sinn von CAPTCHA ist, dass nur ein Mensch diesen Test bestehen können sollte und Bots bzw. irgend eine Form automatisierter Skripte daran versagen. So entsteht ein Wettlauf zwischen CAPTCHA-Anbietern und Hacker-Lösungen, die auf den Einsatz von selbstlernenden Systemen setzen.

Warum müssen wir CAPTCHA lösen?

Heutzutage verwenden die Benutzer automatisierte CAPTCHA-Lösungen für verschiedene Anwendungsfälle. Und hier ein entscheidender Hinweis: Ähnlich wie Penetrationstesting ist der Einsatz gegen Dritte ohne vorherige Genehmigung illegal. Gegen eigene Anwendungen oder gegen Genehmigung (z. B. im Rahmen eines IT-Security-Tests) ist die Anwendung erlaubt. Hacker und Spammer verwenden die CAPTCHA-Bewältigung, um die E-Mail-Adressen der Benutzer zu erhalten, damit sie so viele Spams wie möglich erzeugen können oder um Bruteforce-Attacken durchführen zu können. Die legitimen Beispiele sind Fälle, in denen ein neuer Kunde oder Geschäftspartner zu Ihnen gekommen ist und Zugang zu Ihrer Programmierschnittstelle (API) benötigt, die noch nicht fertig ist oder nicht mit Ihnen geteilt werden kann, wegen eines Sicherheitsproblems oder Missbrauchs, den es verursachen könnte.

Für diese Anwendungsfälle sollen automatisierte Skripte CAPTCHA lösen. Es gibt verschiedene Arten von CAPTCHA: Textbasierte und bildbasierte CAPTCHA, reCAPTCHA und mathematisches CAPTCHA.

Es gibt einen Wettlauf zwischen CAPTCHA-Anbieter und automatisierten Lösungsversuchen. Die in CAPTCHA und reCAPTCHA verwendete Technologie werden deswegen immer intelligenter wird und Aktualisierungen der Zugangsmethoden häufiger. Das Aufrüsten hat begonnen.

Populäre Methoden für die CAPTCHA-Lösung

Die folgenden CAPTCHA-Lösungsmethoden stehen den Benutzern zur Lösung von CAPTCHA und reCAPTCHA zur Verfügung:

OCR (optische Zeichenerkennung) via aktivierte Bots – Dieser spezielle Ansatz löst CAPTCHAs automatisch mit Hilfe der OCR-Technik (Optical Character Recognition). Werkzeuge wie Ocrad, tesseract lösen CAPTCHAs, aber mit sehr geringer Genauigkeit.
Maschinenlernen — Unter Verwendung von Computer Vision, konvolutionalem neuronalem Netzwerk und Python-Frameworks und Bibliotheken wie Keras mit Tensorflow. Wir können tiefe neuronale Konvolutionsnetzmodelle trainieren, um die Buchstaben und Ziffern im CAPTCHA-Bild zu finden.
Online-CAPTCHA-Lösungsdienstleistungen — Diese Dienste verfügen teilweise über menschliche Mitarbeiter, die ständig online verfügbar sind, um CAPTCHAs zu lösen. Wenn Sie Ihre CAPTCHA-Lösungsanfrage senden, übermittelt der Dienst sie an die Lösungsanbieter, die sie lösen und die Lösungen zurückschicken.

Leistungsanalyse der OCR-basierten Lösung

OCR Die OCR ist zwar eine kostengünstige Lösung, wenn es darum geht, eine große Anzahl von trivialen CAPTCHAs zu lösen, aber dennoch liefert sie nicht die erforderliche Genauigkeit. OCR-basierte Lösungen sind nach der Veröffentlichung von ReCaptcha V3 durch Google selten geworden. OCR-fähige Bots sind daher nicht dazu geeignet, CAPTCHA zu umgehen, die von Titanen wie Google, Facebook oder Twitter eingesetzt werden. Hierfür müsste ein besser ausgestattetes CAPTCHA-Lösungssystem eingesetzt werden.

OCR-basierte Lösungen lösen 1 aus 3 trivialen CAPTCHAs korrekt.

Leistungsanalyse der ML-basierten Methode

Schauen wir uns an, wie Lösungen auf dem Prinzip des Maschinenlernens funktionieren:

Die ML-basierte Verfahren verwenden OpenCV, um Konturen in einem Bild zu finden, das die durchgehenden Gebiete feststellt. Die Bilder werden mit der Technik der Schwellenwertbildung vorverarbeitet. Alle Bilder werden in Schwarzweiß konvertiert. Wir teilen das CAPTCHA-Bild mit der OpenCV-Funktion findContour() in verschiedene Buchstaben auf. Die verarbeiteten Bilder sind jetzt nur noch einzelne Buchstaben und Ziffern. Diese werden dann dem CNN-Modell zugeführt, um es zu trainieren. Und das trainierte CNN-Modell ist bereit, die richtige Captchas zu lösen.

Die Präzision einer solchen Lösung ist für alle textbasierten CAPTCHAs weitaus besser als die OCR-Lösung. Es gibt auch viele Nachteile dieser Lösung, denn sie löst nur eine bestimmte Art von CAPTCHAs und Google aktualisiert ständig seinen reCAPTCHA-Generierungsalgorithmus. Die letzte Aktualisierung schien die beste ReCaptcha-Aktualisierung zu sein, die disen Dienst bisher beeinflusst hat: Die regelmäßigen Nutzer hatten dabei kaum eine Veränderung der Schwierigkeit gespürt, während automatisierte Lösungen entweder gar nicht oder nur sehr langsam bzw. inakkurat funktionierten.

Das Modell wurde mit 1⁰⁴ Iterationen mit korrekten und zufälligen Stichproben und 1⁰⁵ Testbildern trainiert, und so wurde eine mittlere Genauigkeit von ~60% erreicht.

Bild-Quelle: “CAPTCHA Recognition with Active Deep Learning” @ TU München https://www.researchgate.net/publication/301620459_CAPTCHA_Recognition_with_Active_Deep_Learning

Wenn Ihr Anwendungsfall also darin besteht, eine Art von CAPTCHA mit ziemlich einfacher Komplexität zu lösen, können Sie ein solches trainiertes ML-Modell hervorragend nutzen. Eine bessere Captcha-Lösungslösung als OCR, muss aber noch eine ganze Menge Bereiche umfassen, um die Genauigkeit der Lösung zu gewährleisten.

Online-Captcha-Lösungsdienst

Online-CAPTCHA-Lösungsdienste sind bisher die bestmögliche Lösung für dieses Problem. Sie verfolgen alle Aktualisierungen von reCAPTCHA durch Google und bieten eine tadellose Genauigkeit von 99%.

Warum sind Online-Anti-Captcha-Dienste leistungsfähiger als andere Methoden?

Die OCR-basierten und ML-Lösungen weisen nach den bisherigen Forschungsarbeiten und Weiterentwicklungen viele Nachteile auf. Sie können nur triviale CAPTCHAs ohne wesentliche Genauigkeit lösen. Hier sind einige Punkte, die in diesem Zusammenhang zu berücksichtigen sind:

– Ein höherer Prozentsatz an korrekten Lösungen (OCR gibt bei wirklich komplizierten CAPTCHAs ein extrem hohes Maß an falschen Antworten; ganz zu schweigen davon, dass einige Arten von CAPTCHA überhaupt nicht mit OCR gelöst werden können, zumindest vorerst).

– Kontinuierlich fehlerfreie Arbeit ohne Unterbrechungen mit schneller Anpassung an die neu hinzugekommene Komplexität.

– Kostengünstig mit begrenzten Ressourcen und geringen Wartungskosten, da es keine Software- oder Hardwareprobleme gibt; alles, was Sie benötigen, ist eine Internetverbindung, um einfache Aufträge über die API des Anti-Captcha-Dienstes zu senden.

Die großen Anbieter von Online-Lösungsdiensten

Jetzt, nachdem wir die bessere Technik zur Lösung Ihrer CAPTCHAs geklärt haben, wollen wir unter allen Anti-Captcha-Diensten den besten auswählen. Einige Dienste bieten eine hohe Genauigkeit der Lösungen, API-Unterstützung für die Automatisierung und schnelle Antworten auf unsere Anfragen. Dazu gehören Dienste wie 2captcha, Imagetyperz, CaptchaSniper, etc.

2CAPTCHA ist einer der Dienste, die auf die Kombination von Machine Learning und echten Menschen setzen, um CAPTCHA zuverlässig zu lösen. Dabei versprechen Dienste wie 2captcha:

Schnelle Lösung mit 17 Sekunden für grafische und textuelle Captchas und ~23 Sekunden für ReCaptcha
Unterstützt alle populären Programmiersprachen mit einer umfassenden Dokumentation der fertigen Bibliotheken.
Hohe Genauigkeit (bis zu 99% je nach dem CAPTCHA-Typ).
Das Geld wird bei falschen Antworten zurückerstattet.
Fähigkeit, eine große Anzahl von Captchas zu lösen (mehr als 10.000 pro Minute)

Schlussfolgerung

Convolutional Neural Networks (CNN) wissen, wie die einfachsten Arten von Captcha zu bewältigen sind und werden auch mit der weiteren Enwicklung schritthalten können. Wir haben es mit einem Wettlauf um verkomplizierte CAPTCHAs und immer fähigeren Lösungen der automatisierten Erkennung zutun. Zur Zeit werden Online-Anti-Captcha-Dienste, die auf einen Mix aus maschinellem Lernen und menschlicher Intelligenz setzen, diesen Lösungen vorerst voraus sein.

Wie funktioniert Natural Language Processing in der Praxis? Ein Überblick

January 24, 2020/in Business Analytics, Data Mining, Data Science, Data Science News, Tutorial/by Aleksandra Klofat

Natural Language Processing (NLP,auf Deutsch auch als Computerlinguistik bezeichnet) gilt als ein Teilbereich des Machine Learning und der Sprachwissenschaften.

Beim NLP geht es vom Prinzip um das Extrahieren und Verarbeiten von Informationen, die in den natürlichen Sprachen enthalten sind. Im Rahmen von NLP wird die natürliche Sprache durch den Rechner in Zahlenabfolgen umgewandelt. Diese Zahlenabfolgen kann wiederum der Rechner benutzen, um Rückschlüsse auf unsere Welt zu ziehen. Kurz gesagt erlaubt NLP dem Computer unsere Sprache in ihren verschiedenen Formen zu verarbeiten.

Eine ausführlichere Definition von NLP wurde auf dem Data Science Blog von Christopher Kipp vorgenommen.

In diesem Beitrag werde ich dagegen einen Überblick über die spezifischen Schritte im NLP als Prozess darstellen, denn NLP erfolgt in mehreren Phasen, die aufeinander Folgen und zum Teil als Kreislauf verstanden werden können. In ihren Grundlagen ähneln sich diese Phasen bei jeder NLP-Anwendung, sei es Chatbot Erstellung oder Sentiment Analyse.

1. Datenreinigung / Normalisierung

In dieser Phase werden die rohen Sprachdaten aus ihrem ursprünglichen Format entnommen, sodass am Ende nur reine Textdaten ohne Format erhalten bleiben.

Beispielsweise können die Textdaten für unsere Analyse aus Webseiten stammen und nach ihrer Erhebung in HTML Code eingebettet sein.

Das Bild zeigt eine Beispielseite. Der Text hier ist noch in einen HTML Kontext eingebettet. Der erste Schritt muss daher sein, den Text von den diversen HTML-Tags zu bereinigen.

2. Tokenisierung und Normalisierung (Tokenizing and Normalizing)

Nach dem ersten Schritt steht als Ergebnis idealerweise reiner Text da, der aber auch Sprachelemente wie Punkte, Kommata sowie Groß- und Kleinschreibung beinhaltet.

Hier kommt der nächste Schritt ins Spiel – die Entfernung der Interpunktion vom Text. Der Text wird auf diese Weise auf seine Wort-Bestandteile (sog. Tokens) reduziert.

Zusätzlich zu diesem Schritt kann auch Groß- und Kleinschreibung entfernt werden (Normalisierung). Dies spart vor allem die Rechenkapazität.

So wird aus folgendem Abschnitt:

Auf diese Weise können wir die Daten aggregieren und in Subsets analysieren. Wir müssen nicht immer das ganze Machine Learning in Hadoop und Spark auf dem gesamten Datensatz starten.

folgender Text

auf diese weise können wir die daten aggregieren und in subsets analysieren wir müssen nicht immer das ganze machine learning in hadoop und spark auf dem gesamten datensatz starten

3. Füllwörterentfernung / Stop words removal

Im nächsten Schritt entfernen wir die sogenannten Füllwörter wie „und“, „sowie“, „etc.“. In den entsprechenden Python Bibliotheken sind die gängigen Füllwörter bereits gespeichert und können leicht entfernt werden. Trotzdem ist hier Vorsicht geboten. Die Bedeutung der Füllwörter in einer Sprache verändert sich je nach Kontext. Aus diesem Grund ist dieser Schritt optional und die zu entfernenden Füllwörter müssen kontextabhängig ausgewählt werden.

Nach diesem Schritt bleibt dann in unserem Beispiel folgender Text erhalten:

können daten aggregieren subsets analysieren müssen nicht immer machine learning hadoop spark datensatz starten

4. Pats of speech (POS)
Als weiterer Schritt können die Wörter mit ihrer korrekten Wortart markiert werden. Der Rechner markiert sie entsprechend als Verben, Nomen, Adjektive etc. Dieser Schritt könnte für manche Fälle der Grundformreduktion/Lemmatization notwendig sein (dazu sogleich unten).

5. Stemming und Lemmatization/Grundformreduktion

In weiteren Schritten kann weiter das sogenannte Stemming und Lemmatization folgen. Vom Prinzip werden hier die einzelnen Wörter in ihre Grundform bzw. Wörterbuchform gebracht.

Im Fall von Stemming werden die Wörter am Ende einfach abgeschnitten und auf den Wortstamm reduziert. So wäre zum Beispiel das Verb „gehen“, „geht“ auf die Form „geh“ reduziert.

Im Fall der Lemmatization bzw. Grundformreduktion werden die Wörter in ihre ursprüngliche Wörterbuchform gebracht: das Verb „geht“ wäre dann ins „gehen“ transformiert.

Parts of Speech, Stemming als auch Lemmatising sind vorteilhaft für die Komplexitätsreduktion. Sie führen deswegen zu mehr Effizienz und schnellerer Anwendbarkeit. Dies geschieht allerdings auf Kosten der Präzision. Die auf diese Weise erstellten Listen können dann im Fall einer Suchmaschine weniger relevante Ergebnisse liefern.

Nachfolgende Schritte beim NLP transformieren den Text in mathematische Zahlenfolgen, die der Rechner verstehen kann. Wie wir in diesem Schritt vorgehen, hängt stark davon ab, was das eigentliche Ziel des Projektes sei. Es gibt ein breites Angebot an Python Paketen, die die Zahlenbildung je nach Projektziel unterschiedlich gestalten

6a. Bag of Words Methoden in Python (https://en.wikipedia.org/wiki/Bag-of-words_model)

Zu den Bag of Words Methoden in Python gehört das sogenannte TF-IDF Vectorizer. Die Transformationsmethode mit dem TF-IDF eignet sich beispielsweise zum Bau eines Spamdetektors, da der TF-IDF Vectorizer die Wörter im Kontext des Gesamtdokumentes betrachtet.

6b. Word Embeddings Methoden in Python: Word2Vec, GloVe (https://en.wikipedia.org/wiki/Word_embedding)

Wie der Name bereits sagt transformiert Word2Vec die einzelnen Wörter zu Vektoren (Zahlenfolgen). Dabei werden ähnliche Wörter zu ähnlichen Vektoren transformiert. Die Methoden aus der Word Embeddings Kiste eignen sich zum Beispiel besser, um einen Chatbot zu erstellen.

Im letzten Schritt des NLP können wir die so prozessierte Sprache in die gängigen Machine Learning Modelle einspeisen. Das Beste an den oben erwähnten NLP Techniken ist die Transformation der Sprache in Zahlensequenzen, die durch jeden ML Algorithmus analysiert werden können. Die weitere Vorgehensweise hängt hier nur noch vom Ziel des Projektes ab.

Dies ist ein Überblick über die notwendigen (und optionalen) Schritte in einem NLP Verfahren. Natürlich hängt die Anwendung vom jeweiligen Use Case ab. Die hier beschriebenen NLP Phasen nehmen viele Ungenauigkeiten in Kauf, wie zum Beispiel die Reduzierung der Wörter auf Wortstämmen bzw. den Verzicht auf Großschreibung. Bei der Umsetzung in der Praxis müssen immer Kosten und Nutzen abgewogen werden und das Verfahren dem besonderen Fall angepasst werden.

Quellen:

Mandy Gu: „Spam or Ham: Introduction to Natural Language Processing Part 2“ https://towardsdatascience.com/spam-or-ham-introduction-to-natural-language-processing-part-2-a0093185aebd
Christopher D. Manning, Prabhakar Raghavan & Hinrich Schütze: „Introduction to Information Retrieval”, Cambridge University Press, https://nlp.stanford.edu/IR-book/
Hobson Lane, Cole Howard, Hannes Max Hapke: „Natural Language Processing in Action. Understanding, analyzing, and generating text with Python.” Manning Shelter Island

Wie passt Machine Learning in eine moderne Data- & Analytics Architektur?

August 22, 2019/in Cloud, Data Engineering, Data Migration, Data Science, Data Science Hack, Insights, Java, Machine Learning, Python, SQL, Tutorial/by Harald Erb

Einleitung

Aufgrund vielfältiger potenzieller Geschäftschancen, die Machine Learning bietet, arbeiten mittlerweile viele Unternehmen an Initiativen für datengetriebene Innovationen. Dabei gründen sie Analytics-Teams, schreiben neue Stellen für Data Scientists aus, bauen intern Know-how auf und fordern von der IT-Organisation eine Infrastruktur für “heavy” Data Engineering & Processing samt Bereitstellung einer Analytics-Toolbox ein. Für IT-Architekten warten hier spannende Herausforderungen, u.a. bei der Zusammenarbeit mit interdisziplinären Teams, deren Mitglieder unterschiedlich ausgeprägte Kenntnisse im Bereich Machine Learning (ML) und Bedarfe bei der Tool-Unterstützung haben. Einige Überlegungen sind dabei: Sollen Data Scientists mit ML-Toolkits arbeiten und eigene maßgeschneiderte Algorithmen nur im Ausnahmefall entwickeln, damit später Herausforderungen durch (unkonventionelle) Integrationen vermieden werden? Machen ML-Funktionen im seit Jahren bewährten ETL-Tool oder in der Datenbank Sinn? Sollen ambitionierte Fachanwender künftig selbst Rohdaten aufbereiten und verknüpfen, um auf das präparierte Dataset einen populären Algorithmus anzuwenden und die Ergebnisse selbst interpretieren? Für die genannten Fragestellungen warten junge & etablierte Software-Hersteller sowie die Open Source Community mit “All-in-one”-Lösungen oder Machine Learning-Erweiterungen auf. Vor dem Hintergrund des Data Science Prozesses, der den Weg eines ML-Modells von der experimentellen Phase bis zur Operationalisierung beschreibt, vergleicht dieser Artikel ausgewählte Ansätze (Notebooks für die Datenanalyse, Machine Learning-Komponenten in ETL- und Datenvisualisierungswerkzeugen vs. Speziallösungen für Machine Learning) und betrachtet mögliche Einsatzbereiche und Integrationsaspekte.

Data Science Prozess und Teams

Im Zuge des Big Data-Hypes kamen neben Design-Patterns für Big Data- und Analytics-Architekturen auch Begriffsdefinitionen auf, die Disziplinen wie Datenintegration von Data Engineering und Data Science voneinander abgrenzen [1]. Prozessmodelle, wie das ab 1996 im Rahmen eines EU-Förderprojekts entwickelte CRISP-DM (CRoss-Industry Standard Process for Data Mining) [2], und Best Practices zur Organisation erfolgreich arbeitender Data Science Teams [3] weisen dabei die Richtung, wie Unternehmen das Beste aus den eigenen Datenschätzen herausholen können. Die Disziplin Data Science beschreibt den, an ein wissenschaftliches Vorgehen angelehnten, Prozess der Nutzung von internen und externen Datenquellen zur Optimierung von Produkten, Dienstleistungen und Prozessen durch die Anwendung statistischer und mathematischer Modelle. Bild 1 stellt in einem Schwimmbahnen-Diagramm einzelne Phasen des Data Science Prozesses den beteiligten Funktionen gegenüber und fasst Erfahrungen aus der Praxis zusammen [5]. Dabei ist die Intensität bei der Zusammenarbeit zwischen Data Scientists und System Engineers insbesondere bei Vorbereitung und Bereitstellung der benötigten Datenquellen und später bei der Produktivsetzung des Ergebnisses hoch. Eine intensive Beanspruchung der Server-Infrastruktur ist in allen Phasen gegeben, bei denen Hands-on (und oft auch massiv parallel) mit dem Datenpool gearbeitet wird, z.B. bei Datenaufbereitung, Training von ML Modellen etc.

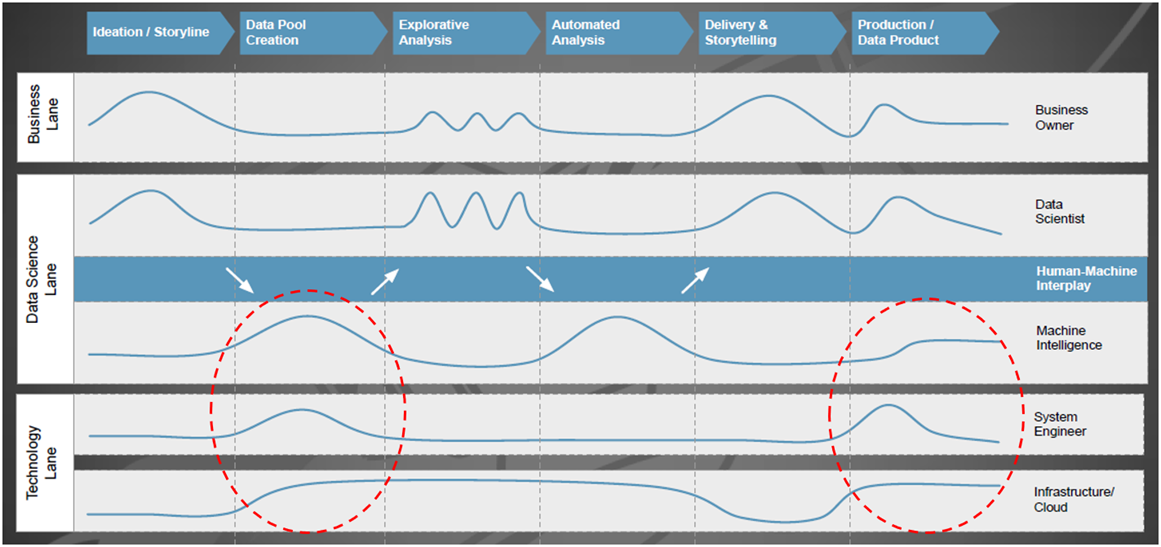
Abbildung 1: Beteiligung und Interaktion von Fachbereichs-/IT-Funktionen mit dem Data Science Team

Mitarbeiter vom Technologie-Giganten Google haben sich reale Machine Learning-Systeme näher angesehen und festgestellt, dass der Umsetzungsaufwand für den eigentlichen Kern (= der ML-Code, siehe den kleinen schwarzen Kasten in der Mitte von Bild 2) gering ist, wenn man dies mit der Bereitstellung der umfangreichen und komplexen Infrastruktur inklusive Managementfunktionen vergleicht [4].

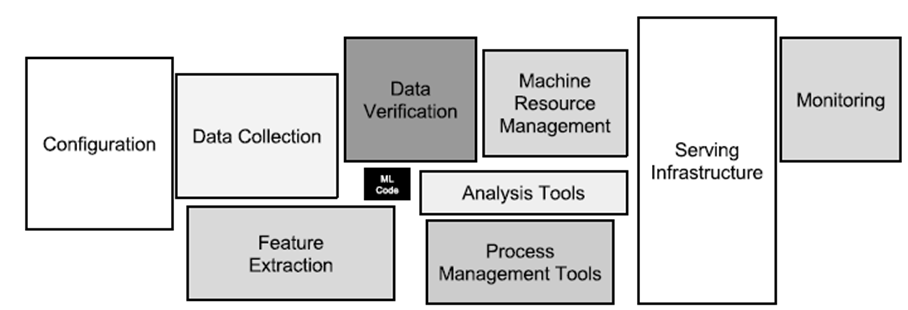
Abbildung 2: Versteckte technische Anforderungen in maschinellen Lernsystemen

Konzeptionelle Architektur für Machine Learning und Analytics

Die Nutzung aller verfügbaren Daten für Analyse, Durchführung von Data Science-Projekten, mit den daraus resultierenden Maßnahmen zur Prozessoptimierung und -automatisierung, bedeutet für Unternehmen sich neuen Herausforderungen zu stellen: Einführung neuer Technologien, Anwendung komplexer mathematischer Methoden sowie neue Arbeitsweisen, die in dieser Form bisher noch nicht dagewesen sind. Für IT-Architekten gibt es also reichlich Arbeit, entweder um eine Data Management-Plattform neu aufzubauen oder um das bestehende Informationsmanagement weiterzuentwickeln. Bild 3 zeigt hierzu eine vierstufige Architektur nach Gartner [6], ausgerichtet auf Analytics und Machine Learning.

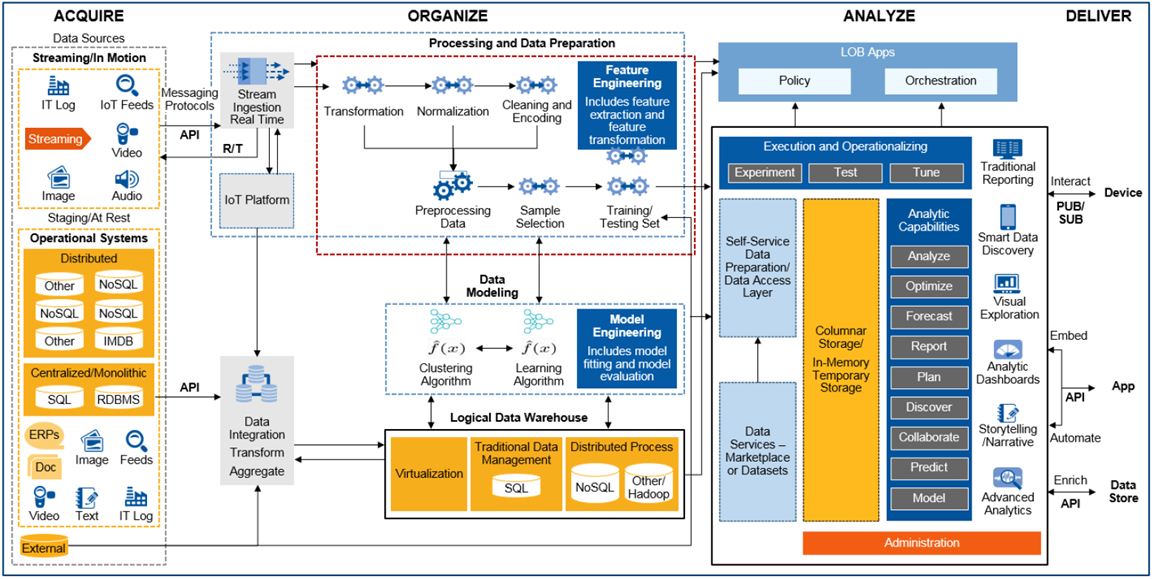
Abbildung 3: Konzeptionelle End-to-End Architektur für Machine Learning und Analytics

Was hat sich im Vergleich zu den traditionellen Data Warehouse- und Business Intelligence-Architekturen aus den 1990er Jahren geändert? Denkt man z.B. an die Präzisionsfertigung eines komplexen Produkts mit dem Ziel, den Ausschuss weiter zu senken und in der Produktionslinie eine höhere Produktivitätssteigerung (Kennzahl: OEE, Operational Equipment Efficiency) erzielen zu können: Die an der Produktherstellung beteiligten Fertigungsmodule (Spezialmaschinen) messen bzw. detektieren über zahlreiche Sensoren Prozesszustände, speicherprogrammierbare Steuerungen (SPS) regeln dazu die Abläufe und lassen zu Kontrollzwecken vom Endprodukt ein oder mehrere hochauflösende Fotos aufnehmen. Bei diesem Szenario entsteht eine Menge interessanter Messdaten, die im operativen Betrieb häufig schon genutzt werden. Z.B. für eine Echtzeitalarmierung bei Über- oder Unterschreitung von Schwellwerten in einem vorher definierten Prozessfenster. Während früher vielleicht aus Kostengründen nur Statusdaten und Störungsinformationen den Weg in relationale Datenbanken fanden, hebt man heute auch Rohdaten, z.B. Zeitreihen (Kraftwirkung, Vorschub, Spannung, Frequenzen,…) für die spätere Analyse auf.

Bezogen auf den Bereich Acquire bewältigt die IT-Architektur in Bild 3 nun Aufgaben, wie die Übernahme und Speicherung von Maschinen- und Sensordaten, die im Millisekundentakt Datenpunkte erzeugen. Während IoT-Plattformen das Registrieren, Anbinden und Management von Hunderten oder Tausenden solcher datenproduzierender Geräte („Things“) erleichtern, beschreibt das zugehörige IT-Konzept den Umgang mit Protokollen wie MQTT, OPC-UA, den Aufbau und Einsatz einer Messaging-Plattform für Publish-/Subscribe-Modelle (Pub/Sub) zur performanten Weiterverarbeitung von Massendaten im JSON-Dateiformat. Im Bereich Organize etablieren sich neben relationalen Datenbanken vermehrt verteilte NoSQL-Datenbanken zum Persistieren eingehender Datenströme, wie sie z.B. im oben beschriebenen Produktionsszenario entstehen. Für hochauflösende Bilder, Audio-, Videoaufnahmen oder andere unstrukturierte Daten kommt zusätzlich noch Object Storage als alternative Speicherform in Frage. Neben der kostengünstigen und langlebigen Datenaufbewahrung ist die Möglichkeit, einzelne Objekte mit Metadaten flexibel zu beschreiben, um damit später die Auffindbarkeit zu ermöglichen und den notwendigen Kontext für die Analysen zu geben, hier ein weiterer Vorteil. Mit dem richtigen Technologie-Mix und der konsequenten Umsetzung eines Data Lake– oder Virtual Data Warehouse-Konzepts gelingt es IT-Architekten, vielfältige Analytics Anwendungsfälle zu unterstützen.

Im Rahmen des Data Science Prozesses spielt, neben der sicheren und massenhaften Datenspeicherung sowie der Fähigkeit zur gleichzeitigen, parallelen Verarbeitung großer Datenmengen, das sog. Feature-Engineering eine wichtige Rolle. Dazu wieder ein Beispiel aus der maschinellen Fertigung: Mit Hilfe von Machine Learning soll nach unbekannten Gründen für den zu hohen Ausschuss gefunden werden. Was sind die bestimmenden Faktoren dafür? Beeinflusst etwas die Maschinenkonfiguration oder deuten Frequenzveränderungen bei einem Verschleißteil über die Zeit gesehen auf ein Problem hin? Maschine und Sensoren liefern viele Parameter als Zeitreihendaten, aber nur einige davon sind – womöglich nur in einer bestimmten Kombination – für die Aufgabenstellung wirklich relevant. Daher versuchen Data Scientists bei der Feature-Entwicklung die Vorhersage- oder Klassifikationsleistung der Lernalgorithmen durch Erstellen von Merkmalen aus Rohdaten zu verbessern und mit diesen den Lernprozess zu vereinfachen. Die anschließende Feature-Auswahl wählt bei dem Versuch, die Anzahl von Dimensionen des Trainingsproblems zu verringern, die wichtigste Teilmenge der ursprünglichen Daten-Features aus. Aufgrund dieser und anderer Arbeitsschritte, wie z.B. Auswahl und Training geeigneter Algorithmen, ist der Aufbau eines Machine Learning Modells ein iterativer Prozess, bei dem Data Scientists dutzende oder hunderte von Modellen bauen, bis die Akzeptanzkriterien für die Modellgüte erfüllt sind. Aus technischer Sicht sollte die IT-Architektur auch bei der Verwaltung von Machine Learning Modellen bestmöglich unterstützen, z.B. bei Modell-Versionierung, -Deployment und -Tracking in der Produktionsumgebung oder bei der Automatisierung des Re-Trainings.

Die Bereiche Analyze und Deliver zeigen in Bild 3 einige bekannte Analysefähigkeiten, wie z.B. die Bereitstellung eines Standardreportings, Self-service Funktionen zur Geschäftsplanung sowie Ad-hoc Analyse und Exploration neuer Datasets. Data Science-Aktivitäten können etablierte Business Intelligence-Plattformen inhaltlich ergänzen, in dem sie durch neuartige Kennzahlen, das bisherige Reporting „smarter“ machen und ggf. durch Vorhersagen einen Blick in die nahe Zukunft beisteuern. Machine Learning-as-a-Service oder Machine Learning-Produkte sind alternative Darreichungsformen, um Geschäftsprozesse mit Hilfe von Analytik zu optimieren: Z.B. integriert in einer Call Center-Applikation, die mittels Churn-Indikatoren zu dem gerade anrufenden erbosten Kunden einen Score zu dessen Abwanderungswilligkeit zusammen mit Handlungsempfehlungen (Gutschein, Rabatt) anzeigt. Den Kunden-Score oder andere Risikoeinschätzungen liefert dabei eine Service Schnittstelle, die von verschiedenen unternehmensinternen oder auch externen Anwendungen (z.B. Smartphone-App) eingebunden und in Echtzeit angefragt werden kann. Arbeitsfelder für die IT-Architektur wären in diesem Zusammenhang u.a. Bereitstellung und Betrieb (skalierbarer) ML-Modelle via REST API’s in der Produktionsumgebung inklusive Absicherung gegen unerwünschten Zugriff.

Ein klassischer Ansatz: Datenanalyse und Machine Learning mit Jupyter Notebook & Python

Jupyter ist ein Kommandozeileninterpreter zum interaktiven Arbeiten mit der Programmiersprache Python. Es handelt sich dabei nicht nur um eine bloße Erweiterung der in Python eingebauten Shell, sondern um eine Softwaresuite zum Entwickeln und Ausführen von Python-Programmen. Funktionen wie Introspektion, Befehlszeilenergänzung, Rich-Media-Einbettung und verschiedene Editoren (Terminal, Qt-basiert oder browserbasiert) ermöglichen es, Python-Anwendungen als auch Machine Learning-Projekte komfortabel zu entwickeln und gleichzeitig zu dokumentieren. Datenanalysten sind bei der Arbeit mit Juypter nicht auf Python als Programmiersprache begrenzt, sondern können ebenso auch sog. Kernels für Julia, R und vielen anderen Sprachen einbinden. Ein Jupyter Notebook besteht aus einer Reihe von “Zellen”, die in einer Sequenz angeordnet sind. Jede Zelle kann entweder Text oder (Live-)Code enthalten und ist beliebig verschiebbar. Texte lassen sich in den Zellen mit einer einfachen Markup-Sprache formatieren, komplexe Formeln wie mit einer Ausgabe in LaTeX darstellen. Code-Zellen enthalten Code in der Programmiersprache, die dem aktiven Notebook über den entsprechenden Kernel (Python 2 Python 3, R, etc.) zugeordnet wurde. Bild 4 zeigt auszugsweise eine Analyse historischer Hauspreise in Abhängigkeit ihrer Lage in Kalifornien, USA (Daten und Notebook sind öffentlich erhältlich [7]). Notebooks erlauben es, ganze Machine Learning-Projekte von der Datenbeschaffung bis zur Evaluierung der ML-Modelle reproduzierbar abzubilden und lassen sich gut versionieren. Komplexe ML-Modelle können in Python mit Hilfe des Pickle Moduls, das einen Algorithmus zur Serialisierung und De-Serialisierung implementiert, ebenfalls transportabel gemacht werden.

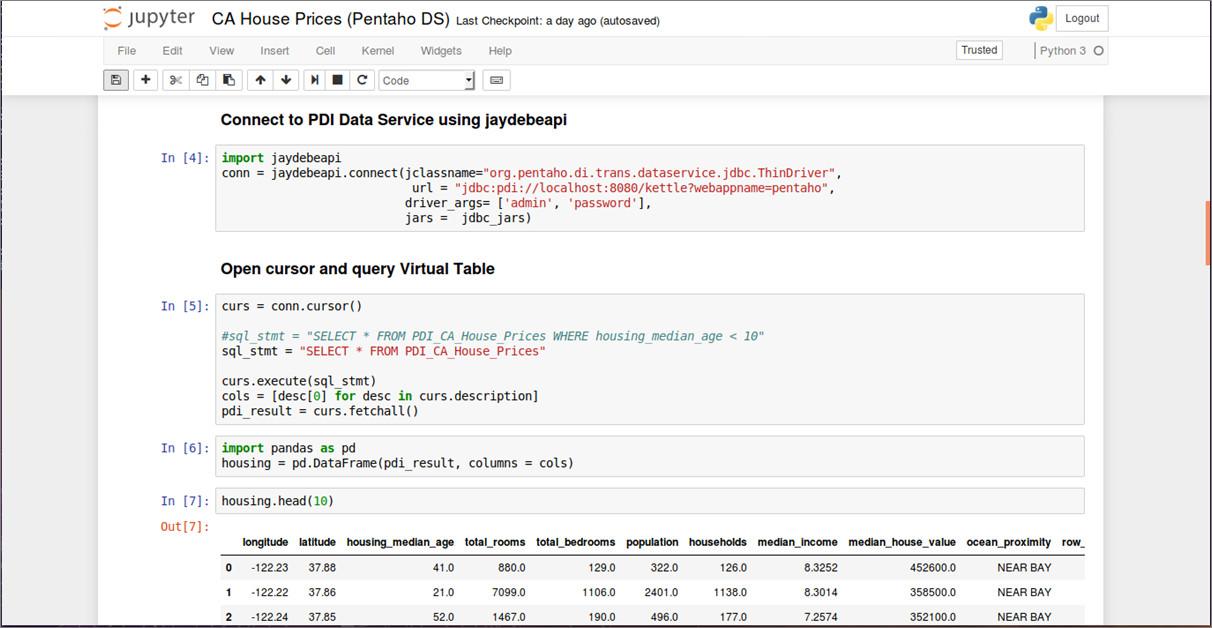
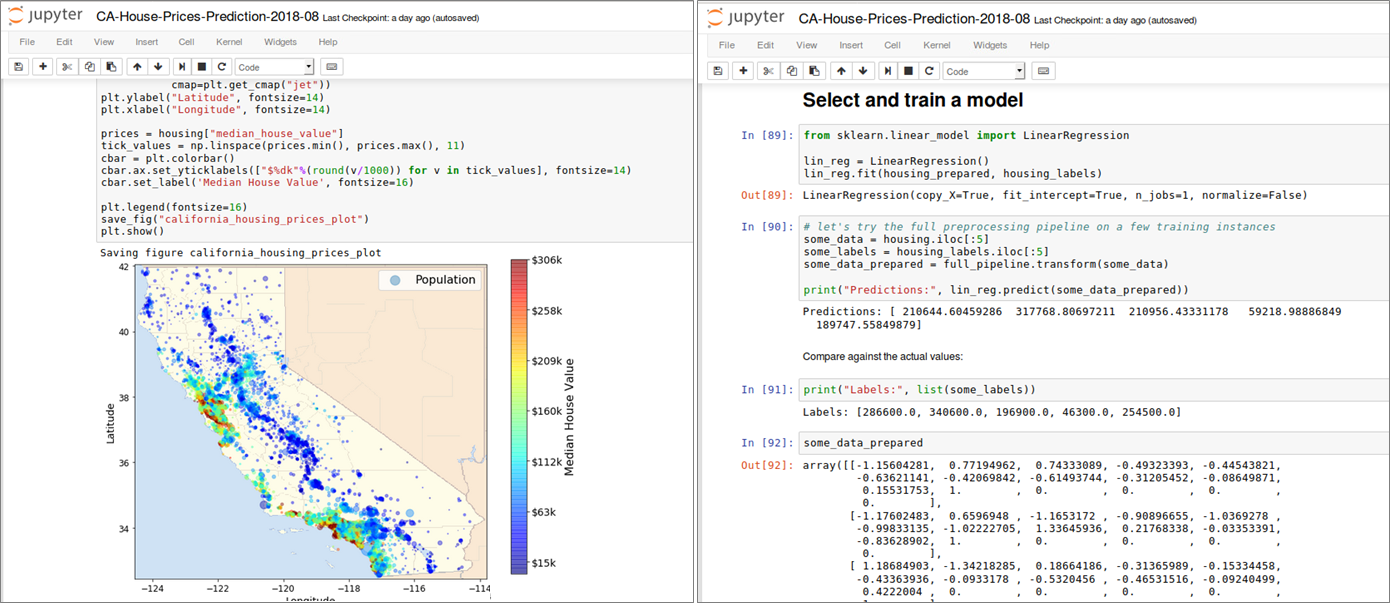
Abbildung 4: Datenbeschaffung, Inspektion, Visualisierung und ML Modell-Training in einem Jupyter Notebook (Pro-grammiersprache: Python)

Ein Problem, auf das man bei der praktischen Arbeit mit lokalen Jupyter-Installationen schnell stößt, lässt sich mit dem “works on my machine”-Syndrom bezeichnen. Kleine Data Sets funktionieren problemlos auf einem lokalen Rechner, wenn sie aber auf die Größe des Produktionsdatenbestandes migriert werden, skaliert das Einlesen und Verarbeiten aller Daten mit einem einzelnen Rechner nicht. Aufgrund dieser Begrenzung liegt der Aufbau einer server-basierten ML-Umgebung mit ausreichend Rechen- und Speicherkapazität auf der Hand. Dabei ist aber die Einrichtung einer solchen ML-Umgebung, insbesondere bei einer on-premise Infrastruktur, eine Herausforderung: Das Infrastruktur-Team muss physische Server und/oder virtuelle Maschinen (VM’s) auf Anforderung bereitstellen und integrieren. Dieser Ansatz ist aufgrund vieler manueller Arbeitsschritte zeitaufwändig und fehleranfällig. Mit dem Einsatz Cloud-basierter Technologien vereinfacht sich dieser Prozess deutlich. Die Möglichkeit, Infrastructure on Demand zu verwenden und z.B. mit einem skalierbaren Cloud-Data Warehouse zu kombinieren, bietet sofortigen Zugriff auf Rechen- und Speicher-Ressourcen, wann immer sie benötigt werden und reduziert den administrativen Aufwand bei Einrichtung und Verwaltung der zum Einsatz kommenden ML-Software. Bild 5 zeigt den Code-Ausschnitt aus einem Jupyter Notebook, das im Rahmen des Cloud Services Amazon SageMaker bereitgestellt wird und via PySpark Kernel auf einen Multi-Node Apache Spark Cluster (in einer Amazon EMR-Umgebung) zugreift. In diesem Szenario wird aus einem Snowflake Cloud Data Warehouse ein größeres Data Set mit 220 Millionen Datensätzen via Spark-Connector komplett in ein Spark Dataframe geladen und im Spark Cluster weiterverarbeitet. Den vollständigen Prozess inkl. Einrichtung und Konfiguration aller Komponenten, beschreibt eine vierteilige Blog-Serie [8]). Mit Spark Cluster sowie Snowflake stehen für sich genommen zwei leistungsfähige Umgebungen für rechenintensive Aufgaben zur Verfügung. Mit dem aktuellen Snowflake Connector für Spark ist eine intelligente Arbeitsteilung mittels Query Pushdown erreichbar. Dabei entscheidet Spark’s optimizer (Catalyst), welche Aufgaben (Queries) aufgrund der effizienteren Verarbeitung an Snowflake delegiert werden [9].

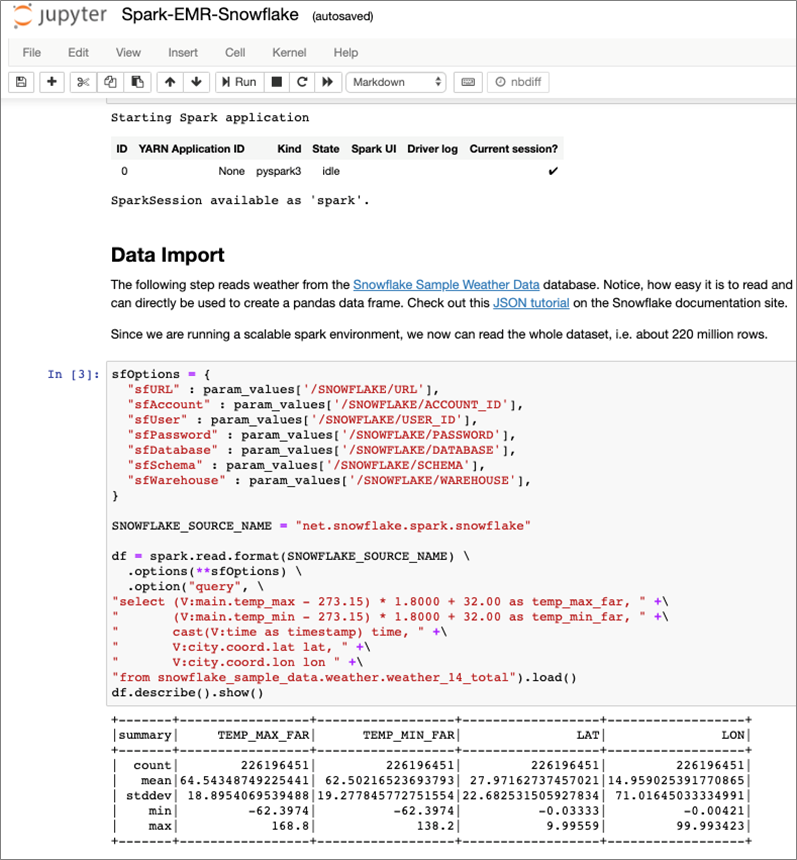
Abbildung 5: Jupyter Notebook in der Cloud – integriert mit Multi-Node Spark Cluster und Snowflake Cloud Data Warehouse

Welches Machine Learning Framework für welche Aufgabenstellung?

Bevor die nächsten Abschnitte weitere Werkzeuge und Technologien betrachten, macht es nicht nur für Data Scientists sondern auch für IT-Architekten Sinn, zunächst einen Überblick auf die derzeit verfügbaren Machine Learning Frameworks zu bekommen. Aus Architekturperspektive ist es wichtig zu verstehen, welche Aufgabenstellungen die jeweiligen ML-Frameworks adressieren, welche technischen Anforderungen und ggf. auch Abhängigkeiten zu den verfügbaren Datenquellen bestehen. Ein gemeinsamer Nenner vieler gescheiterter Machine Learning-Projekte ist häufig die Auswahl des falschen Frameworks. Ein Beispiel: TensorFlow ist aktuell eines der wichtigsten Frameworks zur Programmierung von neuronalen Netzen, Deep Learning Modellen sowie anderer Machine Learning Algorithmen. Während Deep Learning perfekt zur Untersuchung komplexer Daten wie Bild- und Audiodaten passt, wird es zunehmend auch für Use Cases benutzt, für die andere Frameworks besser geeignet sind. Bild 6 zeigt eine kompakte Entscheidungsmatrix [10] für die derzeit verbreitetsten ML-Frameworks und adressiert häufige Praxisprobleme: Entweder werden Algorithmen benutzt, die für den Use Case nicht oder kaum geeignet sind oder das gewählte Framework kann die aufkommenden Datenmengen nicht bewältigen. Die Unterteilung der Frameworks in Small Data, Big Data und Complex Data ist etwas plakativ, soll aber bei der Auswahl der Frameworks nach Art und Volumen der Daten helfen. Die Grenze zwischen Big Data zu Small Data ist dabei dort zu ziehen, wo die Datenmengen so groß sind, dass sie nicht mehr auf einem einzelnen Computer, sondern in einem verteilten Cluster ausgewertet werden müssen. Complex Data steht in dieser Matrix für unstrukturierte Daten wie Bild- und Audiodateien, für die sich Deep Learning Frameworks sehr gut eignen.

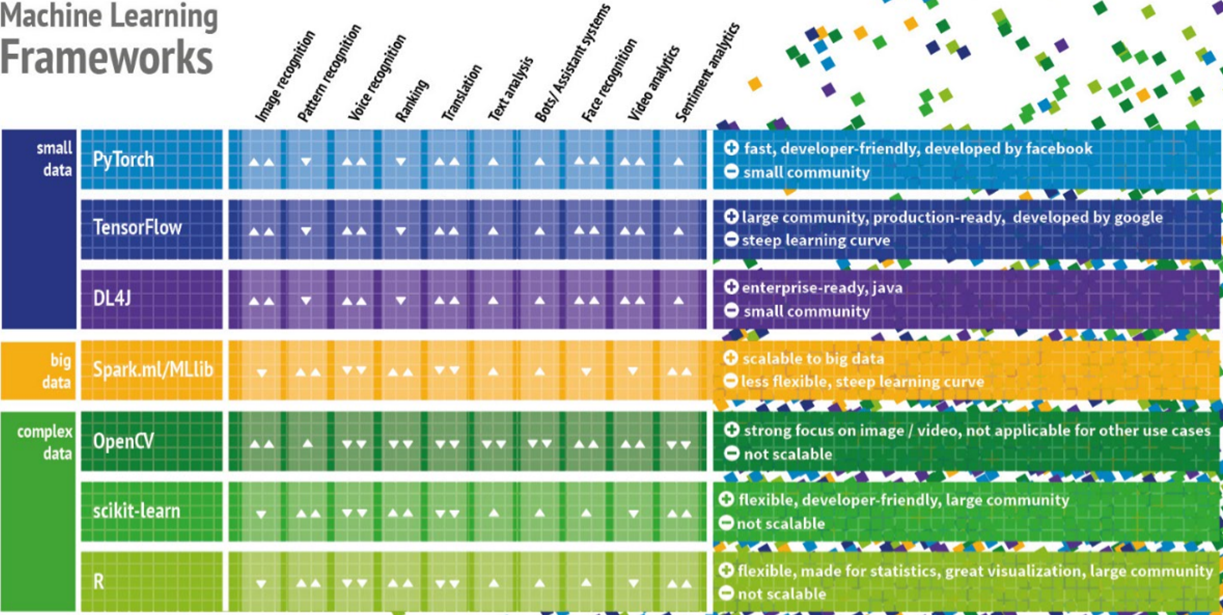
Abbildung 6: Entscheidungsmatrix zu aktuell verbreiteten Machine Learning Frameworks

Self-Service Machine Learning in Business Intelligence-Tools

Mit einfach zu bedienenden Business Intelligence-Werkzeugen zur Datenvisualisierung ist es für Analytiker und für weniger technisch versierte Anwender recht einfach, komplexe Daten aussagekräftig in interaktiven Dashboards zu präsentieren. Hersteller wie Tableau, Qlik und Oracle spielen ihre Stärken insbesondere im Bereich Visual Analytics aus. Statt statische Berichte oder Excel-Dateien vor dem nächsten Meeting zu verschicken, erlauben moderne Besprechungs- und Kreativräume interaktive Datenanalysen am Smartboard inklusive Änderung der Abfragefilter, Perspektivwechsel und Drill-downs. Im Rahmen von Data Science-Projekten können diese Werkzeuge sowohl zur Exploration von Daten als auch zur Visualisierung der Ergebnisse komplexer Machine Learning-Modelle sinnvoll eingesetzt werden. Prognosen, Scores und weiterer ML-Modell-Output lässt sich so schneller verstehen und unterstützt die Entscheidungsfindung bzw. Ableitung der nächsten Maßnahmen für den Geschäftsprozess. Im Rahmen einer IT-Gesamtarchitektur sind Analyse-Notebooks und Datenvisualisierungswerkzeuge für die Standard-Analytics-Toolbox Unternehmens gesetzt. Mit Hinblick auf effiziente Team-Zusammenarbeit, unternehmensinternen Austausch und Kommunikation von Ergebnissen sollte aber nicht nur auf reine Desktop-Werkzeuge gesetzt, sondern Server-Lösungen betrachtet und zusammen mit einem Nutzerkonzept eingeführt werden, um zehnfache Report-Dubletten, konkurrierende Statistiken („MS Excel Hell“) einzudämmen.

Abbildung 7: Datenexploration in Tableau – leicht gemacht für Fachanwender und Data Scientists

Zusätzliche Statistikfunktionen bis hin zur Möglichkeit R- und Python-Code bei der Analyse auszuführen, öffnet auch Fachanwender die Tür zur Welt des Maschinellen Lernens. Bild 7 zeigt das Werkzeug Tableau Desktop mit der Analyse kalifornischer Hauspreise (demselben Datensatz wie oben im Jupyter Notebook-Abschnitt wie in Bild 4) und einer Heatmap-Visualisierung zur Hervorhebung der teuersten Wohnlagen. Mit wenigen Klicks ist auch der Einsatz deskriptiver Statistik möglich, mit der sich neben Lagemaßen (Median, Quartilswerte) auch Streuungsmaße (Spannweite, Interquartilsabstand) sowie die Form der Verteilung direkt aus dem Box-Plot in Bild 7 ablesen und sogar über das Vorhandensein von Ausreißern im Datensatz eine Feststellung treffen lassen. Vorteil dieser Visualisierungen sind ihre hohe Informationsdichte, die allerdings vom Anwender auch richtig interpretiert werden muss. Bei der Beurteilung der Attribute, mit ihren Wertausprägungen und Abhängigkeiten innerhalb des Data Sets, benötigen Citizen Data Scientists (eine Wortschöpfung von Gartner) allerdings dann doch die mathematischen bzw. statistischen Grundlagen, um Falschinterpretationen zu vermeiden. Fraglich ist auch der Nutzen des Data Flow Editors [11] in Oracle Data Visualization, mit dem eins oder mehrere der im Werkzeug integrierten Machine Learning-Modelle trainiert und evaluiert werden können: technisch lassen sich Ergebnisse erzielen und anhand einiger Performance-Metriken die Modellgüte auch bewerten bzw. mit anderen Modellen vergleichen – aber wer kann die erzielten Ergebnisse (wissenschaftlich) verteidigen? Gleiches gilt für die Integration vorhandener R- und Python Skripte, die am Ende dann doch eine Einweisung der Anwender bzgl. Parametrisierung der ML-Modelle und Interpretationshilfen bei den erzielten Ergebnissen erfordern.

Machine Learning in und mit Datenbanken

Die Nutzung eingebetteter 1-click Analytics-Funktionen der oben vorgestellten Data Visualization-Tools ist zweifellos komfortabel und zum schnellen Experimentieren geeignet. Der gegenteilige und eher puristische Ansatz wäre dagegen die Implementierung eigener Machine Learning Modelle in der Datenbank. Für die Umsetzung des gewählten Algorithmus reichen schon vorhandene Bordmittel in der Datenbank aus: SQL inklusive mathematischer und statistische SQL-Funktionen, Tabellen zum Speichern der Ergebnisse bzw. für das ML-Modell-Management und Stored Procedures zur Abbildung komplexer Geschäftslogik und auch zur Ablaufsteuerung. Solange die Algorithmen ausreichend skalierbar sind, gibt es viele gute Gründe, Ihre Data Warehouse Engine für ML einzusetzen:

Einfachheit – es besteht keine Notwendigkeit, eine andere Compute-Plattform zu managen, zwischen Systemen zu integrieren und Daten zu extrahieren, transferieren, laden, analysieren usw.
Sicherheit – Die Daten bleiben dort, wo sie gut geschützt sind. Es ist nicht notwendig, Datenbank-Anmeldeinformationen in externen Systemen zu konfigurieren oder sich Gedanken darüber zu machen, wo Datenkopien verteilt sein könnten.
Performance – Eine gute Data Warehouse Engine verwaltet zur Optimierung von SQL Abfragen viele Metadaten, die auch während des ML-Prozesses wiederverwendet werden könnten – ein Vorteil gegenüber General-purpose Compute Plattformen.

Die Implementierung eines minimalen, aber legitimen ML-Algorithmus wird in [12] am Beispiel eines Entscheidungsbaums (Decision Tree) im Snowflake Data Warehouse gezeigt. Decision Trees kommen für den Aufbau von Regressions- oder Klassifikationsmodellen zum Einsatz, dabei teilt man einen Datensatz in immer kleinere Teilmengen auf, die ihrerseits in einem Baum organisiert sind. Bild 8 zeigt die Snowflake Benutzeroberfläche und ein Ausschnitt von der Stored Procedure, die dynamisch alle SQL-Anweisungen zur Berechnung des Decision Trees nach dem ID3 Algorithmus [13] generiert.

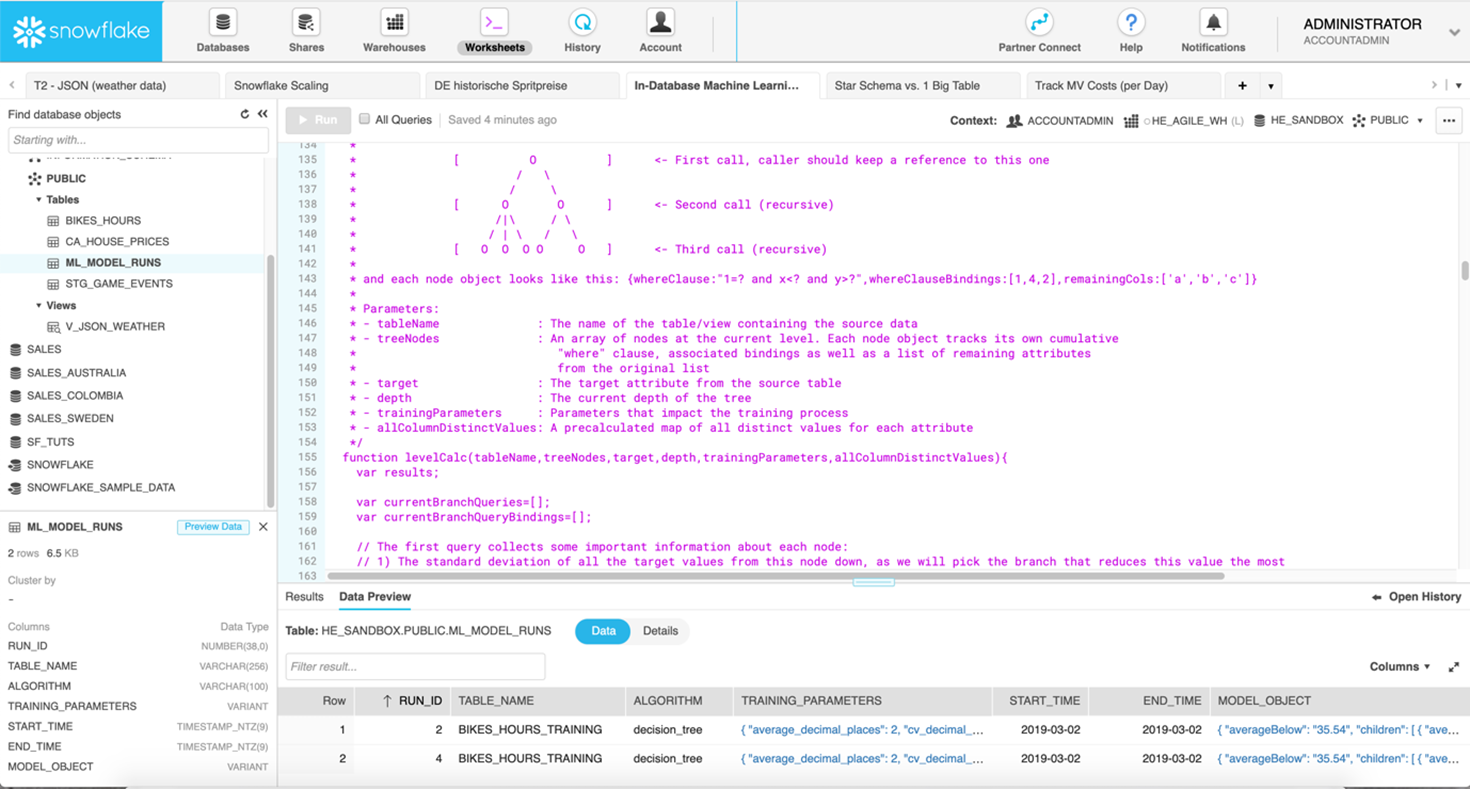
Abbildung 8: Snowflake SQL-Editor mit Stored Procedure zur Berechnung eines Decission Trees

Allerdings ist der Entwicklungs- und Implementierungsprozess für ein Machine Learning Modell umfassender: Es sind relevante Daten zu identifizieren und für das ML-Modell vorzubereiten. Einfach Rohdaten bzw. nicht aggregierten Informationen aus Datenbanktabellen zu extrahieren reicht nicht aus, stattdessen benötigt ein ML-Modell als Input eine flache, meist sehr breite Tabelle mit vielen Aggregaten, die als Features bezeichnet werden. Erst dann kann der Prozess fortgesetzt und der für die Aufgabenstellung ausgewählte Algorithmus trainiert und die Modellgüte bewertet werden. Ist das Ergebnis zufriedenstellend, steht die Implementierung des ML-Modells in der Zielumgebung an und muss sich künftig beim Scoring „frischer Datensätze“ bewähren. Viele zeitaufwändige Teilaufgaben also, bei der zumindest eine Teilautomatisierung wünschenswert wäre. Allein die Datenaufbereitung kann schon bis zu 70…80% der gesamten Projektzeit beanspruchen. Und auch die Implementierung eines ML-Modells wird häufig unterschätzt, da in Produktionsumgebungen der unterstützte Technologie-Stack definiert und ggf. für Machine Learning-Aufgaben erweitert werden muss. Daher ist es reizvoll, wenn das Datenbankmanagement-System auch hier einsetzbar ist – sofern die geforderten Algorithmen dort abbildbar sind. Wie ein ML-Modell für die Kundenabwanderungsprognose (Churn Prediction) werkzeuggestützt mit Xpanse AI entwickelt und beschleunigt im Snowflake Cloud Data Warehouse bereitgestellt werden kann, beschreibt [14] sehr anschaulich: Die benötigten Datenextrakte sind schnell aus Snowflake entladen und stellen den Input für ein neues Xpanse AI-Projekt dar. Sobald notwendige Tabellenverknüpfungen und andere fachliche Informationen hinterlegt sind, analysiert das Tool Datenstrukturen und transformiert alle Eingangstabellen in eine flache Zwischentabelle (u.U. mit Hunderten von Spalten), auf deren Basis im Anschluss ML-Modelle trainiert werden. Nach dem ML-Modell-Training erfolgt die Begutachtung der Ergebnisse: das erstellte Dataset, Güte des ML-Modells und der generierte SQL(!) ETL-Code zur Erstellung der Zwischentabelle sowie die SQL-Repräsentation des ML-Modells, das basierend auf den Input-Daten Wahrscheinlichkeitswerte berechnet und in einer Scoring-Tabelle ablegt. Die Vorteile dieses Ansatzes sind liegen auf der Hand: kürzere Projektzeiten, der Einsatz im Rahmen des Snowflake Cloud Data Warehouse, macht das Experimentieren mit der Zuweisung dedizierter Compute-Ressourcen für die performante Verarbeitung äußerst einfach. Grenzen liegen wiederum bei der zur Verfügung stehenden Algorithmen.

Spezialisierte Software Suites für Machine Learning

Während sich im Markt etablierte Business Intelligence- und Datenintegrationswerkzeuge mit Erweiterungen zur Ausführung von Python- und R-Code als notwendigen Bestandteil der Analyse-Toolbox für den Data Science Prozess positionieren, gibt es daneben auch Machine-Learning-Plattformen, die auf die Arbeit mit künstlicher Intelligenz (KI) zugeschnittenen sind. Für den Einstieg in Data Science bieten sich die oft vorhandenen quelloffenen Distributionen an, die auch über Enterprise-Versionen mit erweiterten Möglichkeiten für beschleunigtes maschinelles Lernen durch Einsatz von Grafikprozessoren (GPUs), bessere Skalierung sowie Funktionen für das ML-Modell Management (z.B. durch Versionsmanagement und Automatisierung) verfügen.

Eine beliebte Machine Learning-Suite ist das Open Source Projekt H2O. Die Lösung des gleichnamigen kalifornischen Unternehmens verfügt über eine R-Schnittstelle und ermöglicht Anwendern dieser statistischen Programmiersprache Vorteile in puncto Performance. Die in H2O verfügbaren Funktionen und Algorithmen sind optimiert und damit eine gute Alternative für das bereits standardmäßig in den R-Paketen verfügbare Funktionsset. H2O implementiert Algorithmen aus dem Bereich Statistik, Data-Mining und Machine Learning (generalisierte Lineare Modelle, K-Means, Random Forest, Gradient Boosting und Deep Learning) und bietet mit einer In-Memory-Architektur und durch standardmäßige Parallelisierung über alle vorhandenen Prozessorkerne eine gute Basis, um komplexe Machine-Learning-Modelle schneller trainieren zu können. Bild 9 zeigt wieder anhand des Datensatzes zur Analyse der kalifornischen Hauspreise die webbasierte Benutzeroberfläche H20 Flow, die den oben beschriebenen Juypter Notebook-Ansatz mit zusätzlich integrierter Benutzerführung für die wichtigsten Prozessschritte eines Machine-Learning-Projektes kombiniert. Mit einigen Klicks kann das California Housing Dataset importiert, in einen H2O-spezifischen Dataframe umgewandelt und anschließend in Trainings- und Testdatensets aufgeteilt werden. Auswahl, Konfiguration und Training der Machine Learning-Modelle erfolgt entweder durch den Anwender im Einsteiger-, Fortgeschrittenen- oder Expertenmodus bzw. im Auto-ML-Modus. Daran anschließend erlaubt H20 Flow die Vorhersage für die Zielvariable (im Beispiel: Hauspreis) für noch unbekannte Datensätze und die Aufbereitung der Ergebnismenge. Welche Unterstützung H2O zur Produktivsetzung von ML-Modellen anbietet, wird an einem Beispiel in den folgenden Abschnitten betrachtet.

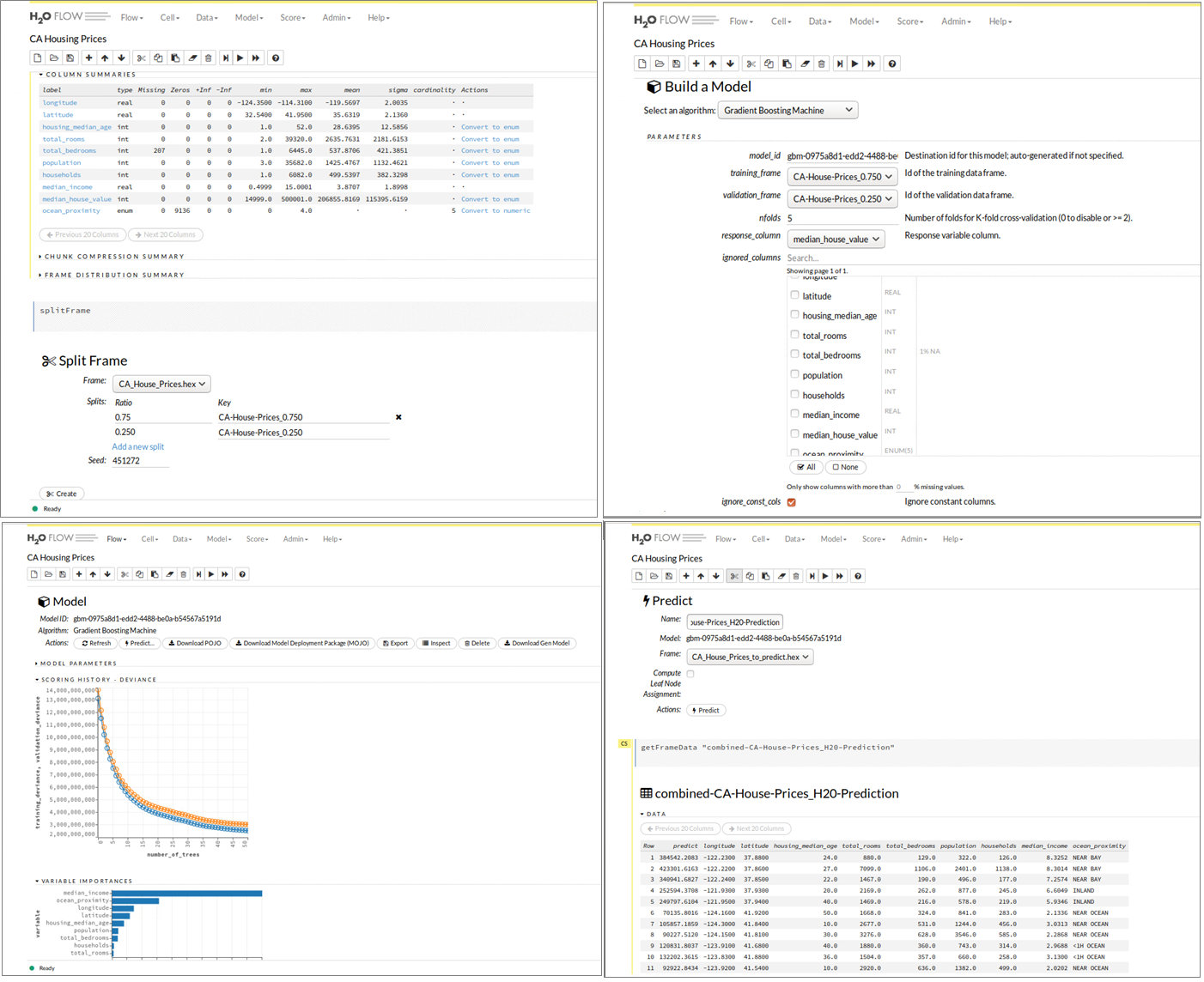
Abbildung 9: H2O Flow Benutzeroberfläche – Datenaufbereitung, ML-Modell-Training und Evaluierung.

Vom Prototyp zur produktiven Machine Learning-Lösung

Warum ist es für viele Unternehmen noch schwer, einen Nutzen aus ihren ersten Data Science-Aktivitäten, Data Labs etc. zu ziehen? In der Praxis zeigt sich, erst durch Operationalisierung von Machine Learning-Resultaten in der Produktionsumgebung entsteht echter Geschäftswert und nur im Tagesgeschäft helfen robuste ML-Modelle mit hoher Güte bei der Erreichung der gesteckten Unternehmensziele. Doch leider erweist sich der Weg vom Prototypen bis hin zum Produktiveinsatz bei vielen Initativen noch als schwierig. Bild 10 veranschaulicht ein typisches Szenario: Data Science-Teams fällt es in ihrer Data Lab-Umgebung technisch noch leicht, Prototypen leistungsstarker ML-Modelle mit Hilfe aktueller ML-Frameworks wie TensorFlow-, Keras- und Word2Vec auf ihren Laptops oder in einer Sandbox-Umgebung zu erstellen. Doch je nach verfügbarer Infrastruktur kann, wegen Begrenzungen bei Rechenleistung oder Hauptspeicher, nur ein Subset der Produktionsdaten zum Trainieren von ML-Modellen herangezogen werden. Ergebnispräsentationen an die Stakeholder der Data Science-Projekte erfolgen dann eher durch Storytelling in MS Powerpoint bzw. anhand eines Demonstrators – selten aber technisch schon so umgesetzt, dass anderere Applikationen z.B. über eine REST-API von dem neuen Risiko Scoring-, dem Bildanalyse-Modul etc. (testweise) Gebrauch machen können. Ausgestattet mit einer Genehmigung vom Management, übergibt das Data Science-Team ein (trainiertes) ML-Modell an das Software Engineering-Team. Nach der Übergabe muss sich allerdings das Engineering-Team darum kümmern, dass das ML-Modell in eine für den Produktionsbetrieb akzeptierte Programmiersprache, z.B. in Java, neu implementiert werden muss, um dem IT-Unternehmensstandard (siehe Line of Governance in Bild 10) bzw. Anforderungen an Skalierbarkeit und Laufzeitverhalten zu genügen. Manchmal sind bei einem solchen Extraschritt Abweichungen beim ML-Modell-Output und in jedem Fall signifikante Zeitverluste beim Deployment zu befürchten.

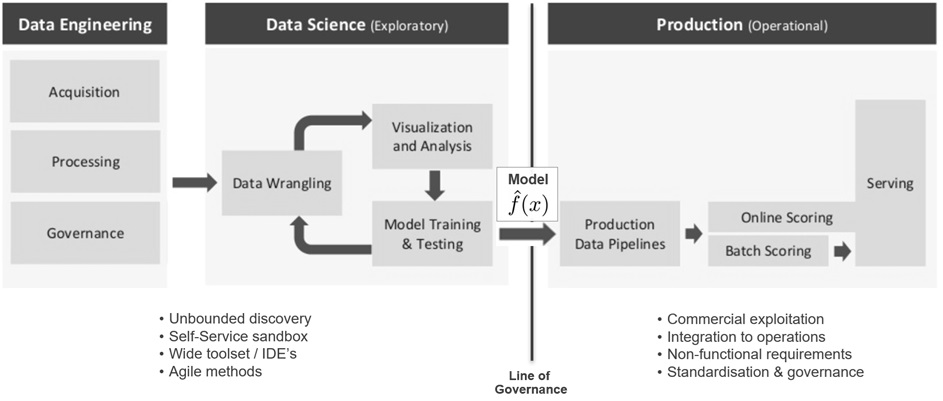
Abbildung 10: Übergabe von Machine Learning-Resultaten zur Produktivsetzung im Echtbetrieb

Unterstützt das Data Science-Team aktiv bei dem Deployment, dann wäre die Einbettung des neu entwickelten ML-Modells in eine Web-Applikation eine beliebte Variante, bei der typischerweise Flask, Tornado (beides Micro-Frameworks für Python) und Shiny (ein auf R basierendes HTML5/CSS/JavaScript Framework) als Technologiekomponenten zum Zuge kommen. Bei diesem Vorgehen müssen ML-Modell, Daten und verwendete ML-Pakete/Abhängigkeiten in einem Format verpackt werden, das sowohl in der Data Science Sandbox als auch auf Produktionsservern lauffähig ist. Für große Unternehmen kann dies einen langwierigen, komplexen Softwareauslieferungsprozess bedeuten, der ggf. erst noch zu etablieren ist. In dem Zusammenhang stellt sich die Frage, wie weit die Erfahrung des Data Science-Teams bei der Entwicklung von Webanwendungen reicht und Aspekte wie Loadbalancing und Netzwerkverkehr ausreichend berücksichtigt? Container-Virtualisierung, z.B. mit Docker, zur Isolierung einzelner Anwendungen und elastische Cloud-Lösungen, die on-Demand benötigte Rechenleistung bereitstellen, können hier Abhilfe schaffen und Teil der Lösungsarchitektur sein. Je nach analytischer Aufgabenstellung ist das passende technische Design [15] zu wählen: Soll das ML-Modell im Batch- oder Near Realtime-Modus arbeiten? Ist ein Caching für wiederkehrende Modell-Anfragen vorzusehen? Wie wird das Modell-Deployment umgesetzt, In-Memory, Code-unabhängig durch Austauschformate wie PMML, serialisiert via R- oder Python-Objekte (Pickle) oder durch generierten Code? Zusätzlich muss für den Produktiveinsatz von ML-Modellen auch an unterstützenden Konzepten zur Bereitstellung, Routing, Versionsmanagement und Betrieb im industriellen Maßstab gearbeitet werden, damit zuverlässige Machine Learning-Produkte bzw. -Services zur internen und externen Nutzung entstehen können (siehe dazu Bild 11)

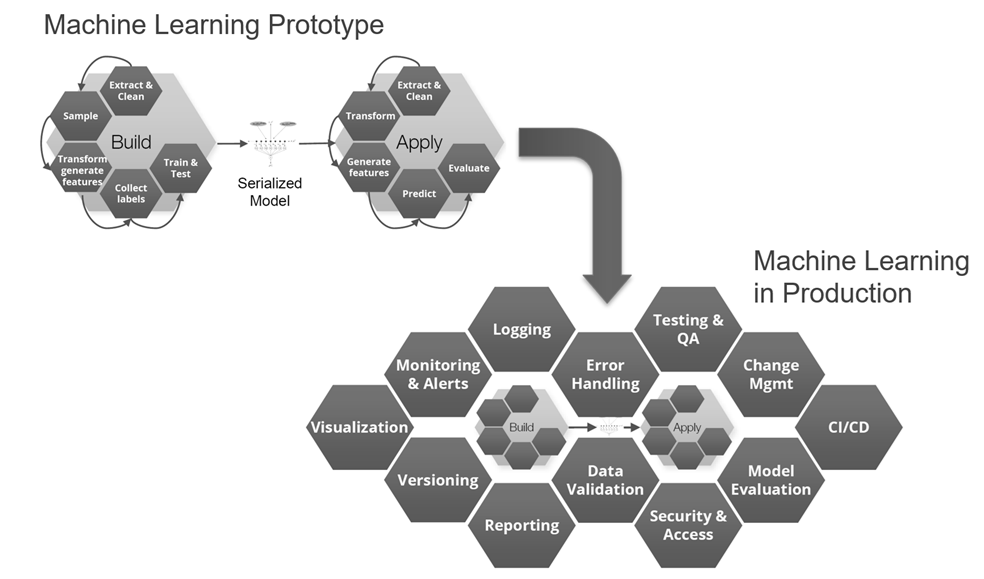
Abbildung 11: Unterstützende Funktionen für produktive Machine Learning-Lösungen

Die Deployment-Variante „Machine Learning Code-Generierung“ lässt sich gut an dem bereits mit H2O Flow besprochenen Beispiel veranschaulichen. Während Bild 9 hierzu die Schritte für Modellaufbau, -training und -test illustriert, zeigt Bild 12 den Download-Vorgang für den zuvor generierten Java-Code zum Aufbau eines ML-Modells zur Vorhersage kalifornischer Hauspreise. In dem generierten Java-Code sind die in H2O Flow vorgenommene Datenaufbereitung sowie alle Konfigurationen für den Gradient Boosting Machine (GBM)-Algorithmus gut nachvollziehbar, Bild 13 gibt mit den ersten Programmzeilen einen ersten Eindruck dazu und erinnert gleichzeitig an den ähnlichen Ansatz der oben mit dem Snowflake Cloud Data Warehouse und dem Tool Xpanse AI bereits beschrieben wurde.

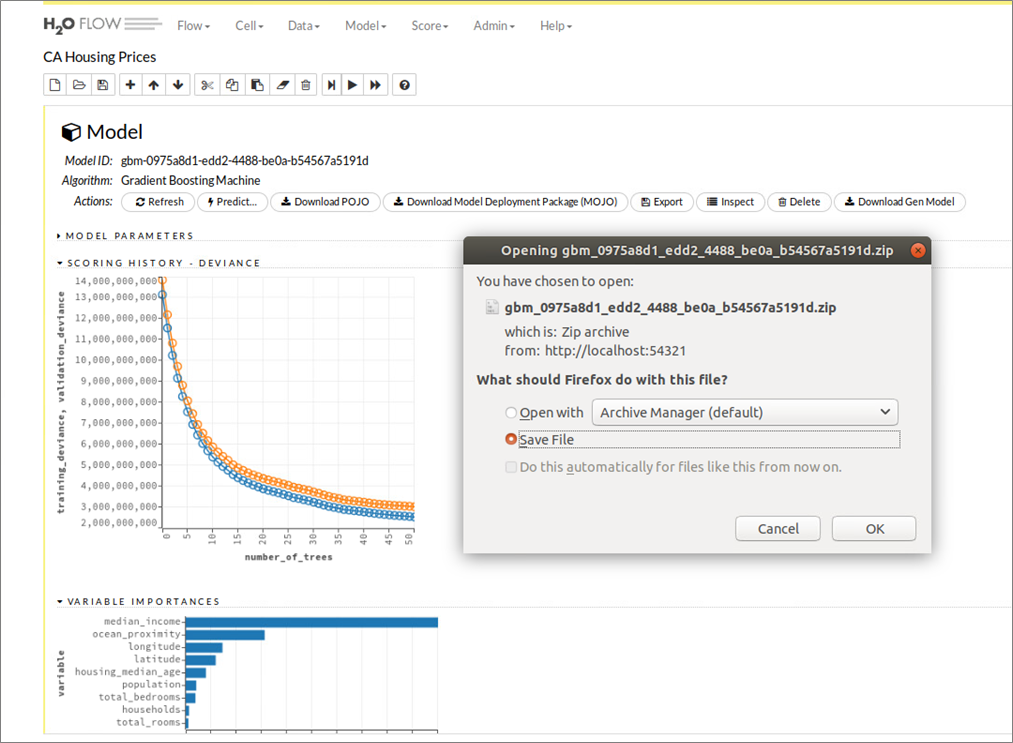
Abbildung 12: H2O Flow Benutzeroberfläche – Java-Code Generierung und Download eines trainierten Models

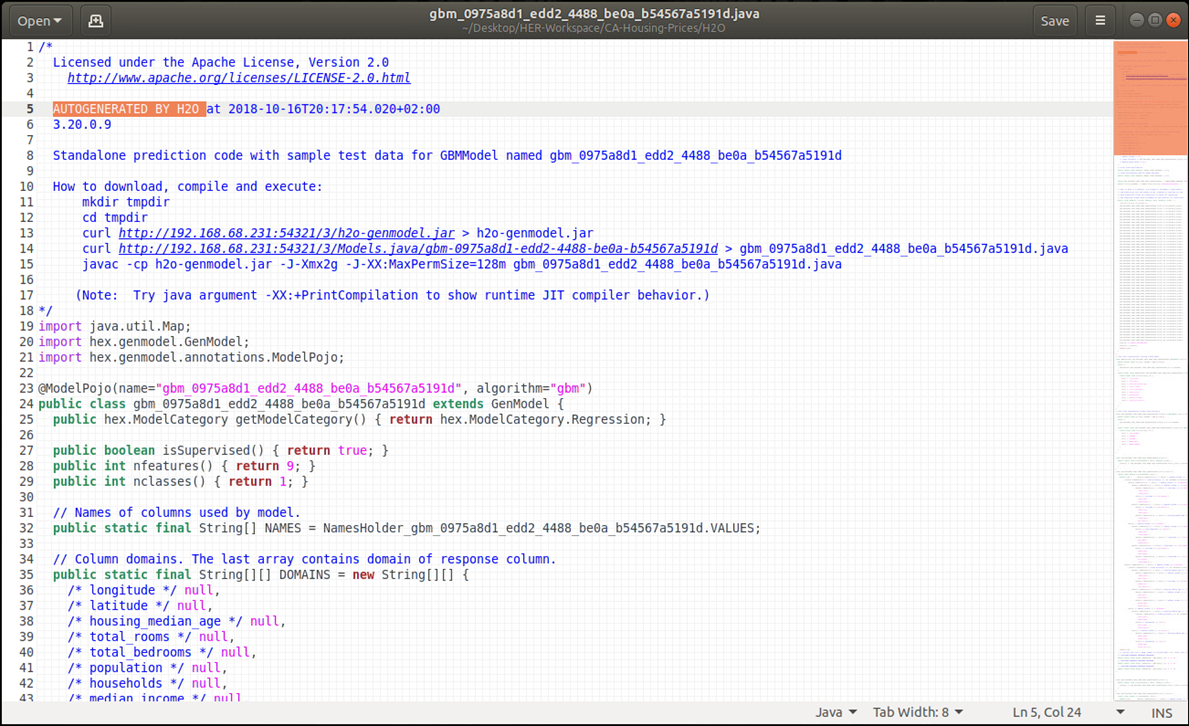
Abbildung 13: Generierter Java-Code eines Gradient Boosted Machine – Modells zur Vorhersage kaliforn. Hauspreise

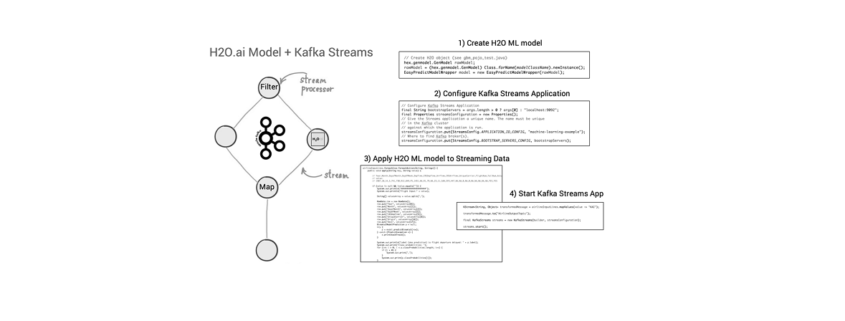
Nach Abschluss der Machine Learning-Entwicklung kann der Java-Code des neuen ML-Modells, z.B. unter Verwendung der Apache Kafka Streams API, zu einer Streaming-Applikation hinzugefügt und publiziert werden [16]. Vorteil dabei: Die Kafka Streams-Applikation ist selbst eine Java-Applikation, in die der generierte Code des ML-Modells eingebettet werden kann (siehe Bild 14). Alle zukünftigen Events, die neue Immobilien-Datensätze zu Häusern aus Kalifornien mit (denselben) Features wie Geoposition, Alter des Gebäudes, Anzahl Zimmer etc. enthalten und als ML-Modell-Input über Kafka Streams hereinkommen, werden mit einer Vorhersage des voraussichtlichen Gebäudepreises von dem auf historischen Daten trainierten ML-Algorithmus beantwortet. Ein Vorteil dabei: Weil die Kafka Streams-Applikation unter der Haube alle Funktionen von Apache Kafka nutzt, ist diese neue Anwendung bereits für den skalierbaren und geschäftskritischen Einsatz ausgelegt.

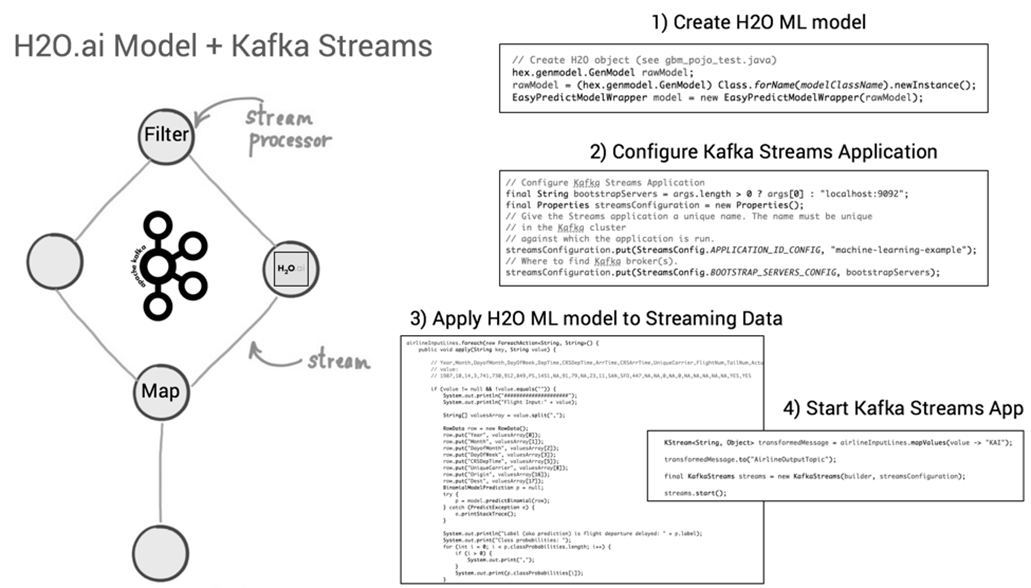
Abbildung 14: Deployment des generierten Java-Codes eines H2O ML-Models in einer Kafka Streams-Applikation

Machine Learning as a Service – “API-first” Ansatz

In den vorherigen Abschnitten kam bereits die Herausforderung zur Sprache, wenn es um die Überführung der Ergebnisse eines Datenexperiments in eine Produktivumgebung geht. Während die Mehrheit der Mitglieder eines Data Science Teams bevorzugt R, Python (und vermehrt Julia) als Programmiersprache einsetzen, gibt es auf der Abnehmerseite das Team der Softwareingenieure, die für technische Implementierungen in der Produktionsumgebung zuständig sind, womöglich einen völlig anderen Technologie-Stack verwenden (müssen). Im Extremfall droht das Neuimplementieren eines Machine Learning-Modells, im besseren Fall kann Code oder die ML-Modellspezifikation transferiert und mit wenig Aufwand eingebettet (vgl. das Beispiel H2O und Apache Kafka Streams Applikation) bzw. direkt in einer neuen Laufzeitumgebung ausführbar gemacht werden. Alternativ wählt man einen „API-first“-Ansatz und entkoppelt das Zusammenwirken von unterschiedlich implementierten Applikationen bzw. -Applikationsteilen via Web-API’s. Data Science-Teams machen hierzu z.B. die URL Endpunkte ihrer testbereiten Algorithmen bekannt, die von anderen Softwareentwicklern für eigene „smarte“ Applikationen konsumiert werden. Durch den Aufbau von REST-API‘s kann das Data Science-Team den Code ihrer ML-Modelle getrennt von den anderen Teams weiterentwickeln und damit eine Arbeitsteilung mit klaren Verantwortlichkeiten herbeiführen, ohne Teamkollegen, die nicht am Machine Learning-Aspekt des eines Projekts beteiligt sind, bei ihrer Arbeit zu blockieren.

Bild 15 zeigt ein einfaches Szenario, bei dem die Gegenstandserkennung von beliebigen Bildern mit einem Deep Learning-Verfahren umgesetzt ist. Einzelne Fotos können dabei via Kommandozeileneditor als Input für die Bildanalyse an ein vortrainiertes Machine Learning-Modell übermittelt werden. Die Information zu den erkannten Gegenständen inkl. Wahrscheinlichkeitswerten kommt dafür im Gegenzug als JSON-Ausgabe zurück. Für die Umsetzung dieses Beispiels wurde in Python auf Basis der Open Source Deep-Learning-Bibliothek Keras, ein vortrainiertes ML-Modell mit Hilfe des Micro Webframeworks Flask über eine REST-API aufrufbar gemacht. Die in [17] beschriebene Applikation kümmert sich außerdem darum, dass beliebige Bilder via cURL geladen, vorverarbeitet (ggf. Wandlung in RGB, Standardisierung der Bildgröße auf 224 x 224 Pixel) und dann zur Klassifizierung der darauf abgebildeten Gegenstände an das ML-Modell übergeben wird. Das ML-Modell selbst verwendet eine sog. ResNet50-Architektur (die Abkürzung steht für 50 Layer Residual Network) und wurde auf Grundlage der öffentlichen ImageNet Bilddatenbank [18] vortrainiert. Zu dem ML-Modell-Input (in Bild 15: Fußballspieler in Aktion) meldet das System für den Tester nachvollziehbare Gegenstände wie Fußball, Volleyball und Trikot zurück, fragliche Klassifikationen sind dagegen Taschenlampe (Torch) und Schubkarre (Barrow).

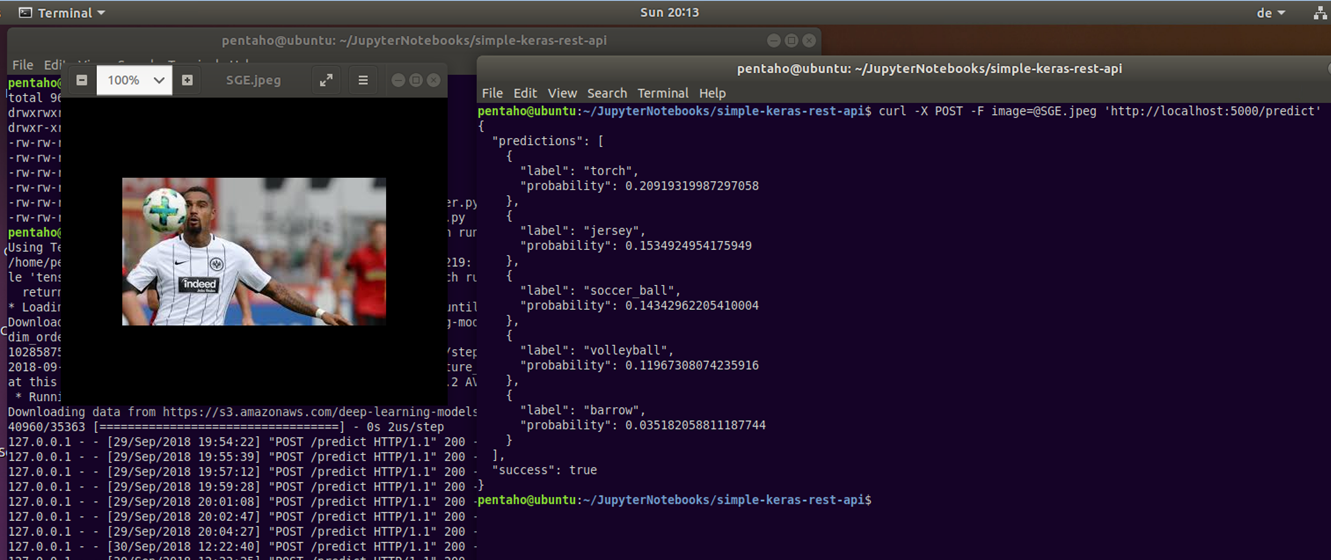
Abbildung 15: Gegenstandserkennung mit Machine Learning und vorgegebenen Bildern via REST-Service

Bei Aufbau und Bereitstellung von Machine Learning-Funktionen mittels REST-API’s bedenken IT-Architekten und beteiligte Teams, ob der Einsatzzweck eher Rapid Prototyping ist oder eine weitreichende Nutzung unterstützt werden muss. Während das oben beschriebene Szenario mit Python, Keras und Flask auf einem Laptop realisierbar ist, benötigen skalierbare Deep Learning Lösungen mehr Aufmerksamkeit hinsichtlich der Deployment-Architektur [19], in dem zusätzlich ein Message Broker mit In-Memory Datastore eingehende bzw. zu analysierende Bilder puffert und dann erst zur Batch-Verarbeitung weiterleitet usw. Der Einsatz eines vorgeschalteten Webservers, Load Balancers, Verwendung von Grafikprozessoren (GPUs) sind weitere denkbare Komponenten für eine produktive ML-Architektur.

Als abschließendes Beispiel für einen leistungsstarken (und kostenpflichtigen) Machine Learning Service soll die Bildanalyse von Google Cloud Vision [20] dienen. Stellt man dasselbe Bild mit der Fußballspielszene von Bild 15 und Bild 16 bereit, so erkennt der Google ML-Service neben den Gegenständen weit mehr Informationen: Kontext (Teamsport, Bundesliga), anhand der Gesichtserkennung den Spieler selbst und aktuelle bzw. vorherige Mannschaftszugehörigkeiten usw. Damit zeigt sich am Beispiel des Tech-Giganten auch ganz klar: Es kommt vorallem auf die verfügbaren Trainingsdaten an, inwieweit dann mit Algorithmen und einer dazu passenden Automatisierung (neue) Erkenntnisse ohne langwierigen und teuren manuellen Aufwand gewinnen kann. Einige Unternehmen werden feststellen, dass ihr eigener – vielleicht einzigartige – Datenschatz einen echten monetären Wert hat?

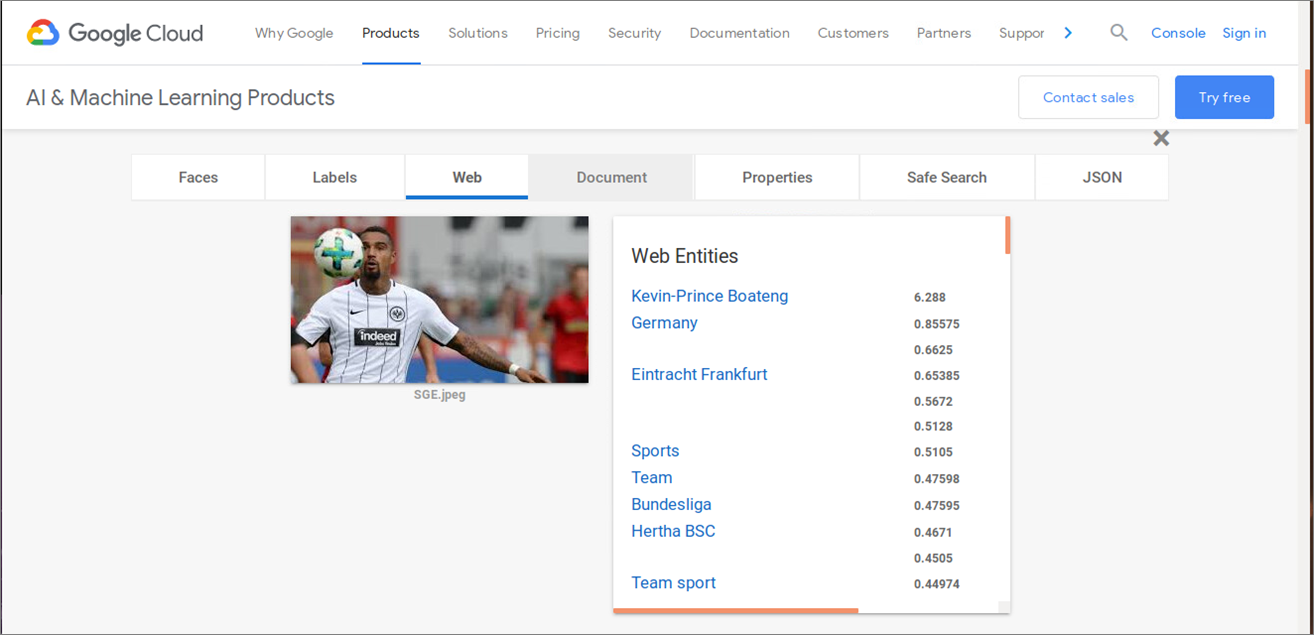
Abbildung 16: Machine Learning Bezahlprodukt (Google Vision)

Fazit

Machine Learning ist eine interessante “Challenge” für Architekten. Folgende Punkte sollte man bei künftigen Initativen berücksichtigen:

Finden Sie das richtige Geschäftsproblem bzw geeignete Use Cases
Identifizieren und definieren Sie die Einschränkungen (Sind z.B. genug Daten vorhanden?) für die zu lösende Aufgabenstellung
Nehmen Sie sich Zeit für das Design von Komponenten und Schnittstellen
Berücksichtigen Sie frühzeitig mögliche organisatorische Gegebenheiten und Einschränkungen
Denken Sie nicht erst zum Schluss an die Produktivsetzung Ihrer analytischen Modelle oder Machine Learning-Produkte
Der Prozess ist insgesamt eine Menge Arbeit, aber es ist keine Raketenwissenschaft.

Quellenverzeichnis

[1]	Bill Schmarzo: “What’s the Difference Between Data Integration and Data Engineering?”, LinkedIn Pulse -> Link, 2018
[2]	William Vorhies: “CRISP-DM – a Standard Methodology to Ensure a Good Outcome”, Data Science Central -> Link, 2016
[3]	Bill Schmarzo: “A Winning Game Plan For Building Your Data Science Team”, LinkedIn Pulse -> Link, 2018
[4]	D. Sculley, G. Holt, D. Golovin, E. Davydov, T. Phillips, D. Ebner, V. Chaudhary, M. Young, J.-F. Crespo, D. Dennison: “Hidden technical debt in Machine learning systems”. In NIPS’15 Proceedings of the 28th International Conference on Neural Information Processing Systems – Volume 2, 2015
[5]	K. Bollhöfer: „Data Science – the what, the why and the how!“, Präsentation von The unbelievable Machine Company, 2015
[6]	Carlton E. Sapp: “Preparing and Architecting for Machine Learning”, Gartner, 2017
[7]	A. Geron: “California Housing” Dataset, Jupyter Notebook. GitHub.com -> Link, 2018
[8]	R. Fehrmann: “Connecting a Jupyter Notebook to Snowflake via Spark” -> Link, 2018
[9]	E. Ma, T. Grabs: „Snowflake and Spark: Pushing Spark Query Processing to Snowflake“ -> Link, 2017
[10]	Dr. D. James: „Entscheidungsmatrix „Machine Learning“, it-novum.com -> Link, 2018
[11]	Oracle Analytics@YouTube: “Oracle DV – ML Model Comparison Example”, Video -> Link
[12]	J. Weakley: Machine Learning in Snowflake, Towards Data Science Blog -> Link, 2019
[13]	Dr. S. Sayad: An Introduction to Data Science, Website -> Link, 2019
[14]	U. Bethke: Build a Predictive Model on Snowflake in 1 day with Xpanse AI, Blog à Link, 2019
[15]	Sergei Izrailev: Design Patterns for Machine Learning in Production, Präsentation H2O World, 2017
[16]	K. Wähner: How to Build and Deploy Scalable Machine Learning in Production with Apache Kafka, Confluent Blog -> Link, 2017
[17]	A. Rosebrock: “Building a simple Keras + deep learning REST API”, The Keras Blog -> Link, 2018
[18]	Stanford Vision Lab, Stanford University, Princeton University: Image database, Website -> Link
[19]	A. Rosebrock: “A scalable Keras + deep learning REST API”, Blog -> Link, 2018
[20]	Google Cloud Vision API (Beta Version) -> Link, abgerufen 2018

Fehler-Rückführung mit der Backpropagation

January 29, 2019/in Artificial Intelligence, Deep Learning, Machine Learning, Main Category, Mathematics, Predictive Analytics/by Benjamin Aunkofer

Dies ist Artikel 4 von 6 der Artikelserie –Einstieg in Deep Learning.

Das Gradienten(abstiegs)verfahren ist der Schlüssel zum Training einzelner Neuronen bzw. deren Gewichtungen zu den Neuronen der vorherigen Schicht. Wer dieses Prinzip verstanden hat, hat bereits die halbe Miete zum Verständnis des Trainings von künstlichen neuronalen Netzen.

Der Gradientenabstieg wird häufig fälschlicherweise mit der Backpropagation gleichgesetzt, jedoch ist das nicht ganz richtig, denn die Backpropagation ist mehr als die Anwendung des Gradientenabstiegs.

Bevor wir die Backpropagation erläutern, nochmal kurz zurück zur Forward-Propagation, die die eigentliche Prädiktion über ein künstliches neuronales Netz darstellt:

Forward-Propagation

Abbildung 1: Ein simples kleines künstliches neuronales Netz mit zwei Schichten (+ Eingabeschicht) und zwei Neuronen pro Schicht.

In einem kleinen künstlichen neuronalen Netz, wie es in der Abbildung 1 dargestellt ist, und das alle Neuronen über die Sigmoid-Funktion aktiviert, wird jedes Neuron eine Nettoeingabe $z$ berechnen…

$z = w^{T} \cdot x$

… und diese Nettoeingabe in die Sigmoid-Funktion einspeisen…

$\phi(z) = sigmoid(z) = \frac{1}{1 + e^{-z}}$

… die dann das einzelne Neuron aktiviert. Die Aktivierung erfolgt also in der mittleren Schicht (N-Schicht) wie folgt:

$N_{j} = \frac{1}{1 + e^{- \sum (w_{ij} \cdot x_{i}) }}$

Die beiden Aktivierungsausgaben $N$ werden dann als Berechnungsgrundlage für die Ausgaben der Ausgabeschicht $o$ verwendet. Auch die Ausgabe-Neuronen berechnen ihre jeweilige Nettoeingabe $z$ und aktivieren über Sigmoid( $z$ ).

Ausgabe eines Ausgabeknotens als Funktion der Eingänge und der Verknüpfungsgewichte für ein dreischichtiges neuronales Netz, mit nur zwei Knoten je Schicht, kann also wie folgt zusammen gefasst werden:

$O_{k} = \frac{1}{1 + e^{- \sum (w_{jk} \cdot \frac{1}{1 + e^{- \sum (w_{ij} \cdot x_{i}) }}) }}$

Abbildung 2: Forward-Propagation. Aktivierung via Sigmoid-Funktion.

Sollte dies die erste Forward-Propagation gewesen sein, wird der Output noch nicht auf den Input abgestimmt sein. Diese Abstimmung erfolgt in Form der Gewichtsanpassung im Training des neuronalen Netzes, über die zuvor erwähnte Gradientenmethode. Die Gradientenmethode ist jedoch von einem Fehler abhängig. Diesen Fehler zu bestimmen und durch das Netz zurück zu führen, das ist die Backpropagation.

Back-Propagation

Um die Gewichte entgegen des Fehlers anpassen zu können, benötigen wir einen möglichst exakten Fehler als Eingabe. Der Fehler berechnet sich an der Ausgabeschicht über eine Fehlerfunktion (Loss Function), beispielsweise über den MSE (Mean Squared Error) oder über die sogenannte Kreuzentropie (Cross Entropy). Lassen wir es in diesem Beispiel einfach bei einem simplen Vergleich zwischen dem realen Wert (Sollwert $o_{real}$ ) und der Prädiktion (Ausgabe $o$ ) bleiben:

$e_{o} = o_{real} - o$

Der Fehler $e$ ist also einfach der Unterschied zwischen dem Ziel-Wert und der Prädiktion. Jedes Training ist eine Wiederholung von Prädiktion (Forward) und Gewichtsanpassung (Back). Im ersten Schritt werden üblicherweise die Gewichtungen zufällig gesetzt, jede Gewichtung unterschiedlich nach Zufallszahl. So ist die Wahrscheinlichkeit, gleich zu Beginn die “richtigen” Gewichtungen gefunden zu haben auch bei kleinen neuronalen Netzen verschwindend gering. Der Fehler wird also groß sein und kann über den Gradientenabstieg durch Gewichtsanpassung verkleinert werden.

In diesem Beispiel berechnen wir die Fehler $e_{1}$ und $e_{2}$ und passen danach die Gewichte $w_{j,k}$ ( $w_{1,1}$ & $w_{2,1}$ und $w_{1,2}$ & $w_{2,2}$ ) der Schicht zwischen dem Hidden-Layer $N$ und dem Output-Layer $o$ an.

Abbildung 3: Anpassung der Gewichtungen basierend auf dem Fehler in der Ausgabe-Schicht.

Die Frage ist nun, wie die Gewichte zwischen dem Input-Layer $X$ und dem Hidden-Layer $N$ anzupassen sind. Es stellt sich die Frage, welchen Einfluss diese auf die Fehler in der Ausgabe-Schicht haben?

Um diese Gewichtungen anpassen zu können, benötigen wir den Fehler-Anteil der beiden Neuronen $N_{1}$ und $N_{2}$ . Dieser Anteil am Fehler der jeweiligen Neuronen ergibt sich direkt aus den Gewichtungen $w_{j,k}$ zum Output-Layer:

$e_{N_{1}} = e_{o1} \cdot \frac{w_{1,1}}{w_{1,1} + w_{1,2}} + e_{o2} \cdot \frac{w_{1,2}}{w_{1,1} + w_{1,2}}$

$e_{N_{2}} = e_{o1} \cdot \frac{w_{2,1}}{w_{2,1} + w_{2,2}} + e_{o2} \cdot \frac{w_{2,2}}{w_{2,1} + w_{2,2}}$

Wenn man das nun generalisiert:

$e_{N} = \left(\begin{array}{rr} \frac{w_{1,1}}{w_{1,1} + w_{1,2}} & \frac{w_{1,2}}{w_{1,1} + w_{1,2}} \\ \frac{w_{2,1}}{w_{2,1} + w_{2,2}} & \frac{w_{2,2}}{w_{2,1} + w_{2,2}} \end{array}\right) \cdot \left(\begin{array}{c} e_{1} \\ e_{2} \end{array}\right) \qquad$

Dabei ist es recht aufwändig, die Gewichtungen stets ins Verhältnis zu setzen. Diese Berechnung können wir verkürzen, indem ganz einfach direkt nur die Gewichtungen ohne Relativierung zur Kalkulation des Fehleranteils benutzt werden. Die Relationen bleiben dabei erhalten!

$e_{N} = \left(\begin{array}{rr} w_{1,1} & w_{1,2} \\ w_{2,1} & w_{2,2} \end{array}\right) \cdot \left(\begin{array}{c} e_{1} \\ e_{2} \end{array}\right) \qquad$

Oder folglich in Kurzform: $e_{N} = w^{T} \cdot e_{o}$

Abbildung 4: Vollständige Gewichtsanpassung auf Basis der Fehler in der Ausgabeschicht und der Fehleranteile in der verborgenden Schicht.

Und nun können, basierend auf den Fehleranteilen der verborgenden Schicht $N$ , die Gewichtungen $w_{i,j}$ zwischen der Eingabe-Schicht $I$ und der verborgenden Schicht $N$ angepasst werden, entgegen dieser Fehler $e_{N}$ .

Die Backpropagation besteht demnach aus zwei Schritten:

Fehler-Berechnung durch Abgleich der Soll-Werte mit den Prädiktionen in der Ausgabeschicht und durch Fehler-Rückführung zu den Neuronen der verborgenden Schichten (Hidden-Layer)
Anpassung der Gewichte entgegen des Gradientenanstiegs der Fehlerfunktion (Loss Function)

Buchempfehlungen

Die folgenden zwei Bücher haben mir sehr beim Verständnis und beim Verständlichmachen der Backpropagation in künstlichen neuronalen Netzen geholfen.


Neuronale Netze selbst programmieren: Ein verständlicher Einstieg mit Python	Deep Learning. Das umfassende Handbuch: Grundlagen, aktuelle Verfahren und Algorithmen, neue Forschungsansätze (mitp Professional)

Training eines Neurons mit dem Gradientenverfahren

January 13, 2019/in Artificial Intelligence, Data Science, Data Science Hack, Deep Learning, Machine Learning, Main Category, Mathematics, optimization, Predictive Analytics, Python/by Benjamin Aunkofer

Dies ist Artikel 3 von 6 der Artikelserie –Einstieg in Deep Learning.

Das Training von neuronalen Netzen erfolgt nach der Forward-Propagation über zwei Schritte:

Fehler-Rückführung über aller aktiver Neuronen aller Netz-Schichten, so dass jedes Neuron “seinen” Einfluss auf den Ausgabefehler kennt.
Anpassung der Gewichte entgegen den Gradienten der Fehlerfunktion

Beide Schritte werden in der Regel zusammen als Backpropagation bezeichnet. Machen wir erstmal einen Schritt vor und betrachten wir, wie ein Neuron seine Gewichtsverbindungen zu seinen Vorgängern anpasst.

Gradientenabstiegsverfahren

Der Gradientenabstieg ist ein generalisierbarer Algorithmus zur Optimierung, der in vielen Verfahren des maschinellen Lernens zur Anwendung kommt, jedoch ganz besonders als sogenannte Backpropagation im Deep Learning den Erfolg der künstlichen neuronalen Netze erst möglich machen konnte.

Der Gradientenabstieg lässt sich vom Prinzip her leicht erklären: Angenommen, man stünde im Gebirge im dichten Nebel. Das Tal, und somit der Weg nach Hause, ist vom Nebel verdeckt. Wohin laufen wir? Wir können das Ziel zwar nicht sehen, tasten uns jedoch so heran, dass unser Gehirn den Gradienten (den Unterschied der Höhen beider Füße) berechnet, somit die Steigung des Bodens kennt und sich entgegen dieser Steigung unser Weg fortsetzt.

Konkret funktioniert der Gradientenabstieg so: Wir starten bei einem zufälligen Theta $\theta$ (Random Initialization). Wir berechnen die Ausgabe (Forwardpropogation) und vergleichen sie über eine Verlustfunktion (z. B. über die Funktion Mean Squared Error) mit dem tatsächlich korrekten Wert. Auf Grund der zufälligen Initialisierung haben wir eine nahe zu garantierte Falschheit der Ergebnisse und somit einen Verlust. Für die Verlustfunktion berechnen wir den Gradienten für gegebene Eingabewerte. Voraussetzung dafür ist, dass die Funktion ableitbar ist. Wir bewegen uns entgegen des Gradienten in Richtung Minimum der Verlustfunktion. Ist dieses Minimum (fast) gefunden, spricht man auch davon, dass der Lernalgorithmus konvergiert.

Das Gradientenabstiegsverfahren ist eine Möglichkeit der Gradientenverfahren, denn wollten wir maximieren, würden wir uns entlang des Gradienten bewegen, was in anderen Anwendungen sinnvoll ist.

Ob als “Cost Function” oder als “Loss Function” bezeichnet, in jedem Fall ist es eine “Error Function”, aber auf die Benennung kommen wir später zu sprechen. Jedenfalls versuchen wir die Fehlerrate zu senken! Leider sind diese Funktionen in der Praxis selten so einfach konvex (zwei Berge mit einem Tal dazwischen).

Aber Achtung: Denn befinden wir uns nur zwischen zwei Bergen, finden wir das Tal mit Sicherheit über den Gradienten. Befinden wir uns jedoch in einem richtigen Gebirge mit vielen Bergen und Tälern, gilt es, das richtige Tal zu finden. Bei der Optimierung der Gewichtungen von künstlichen neuronalen Netzen wollen wir die besten Gewichtungen finden, die uns zu den geringsten Ausgaben der Verlustfunktion führen. Wir suchen also das globale Minimum unter den vielen (lokalen) Minima.

Programmier-Beispiel in Python

Nachfolgend ein Beispiel des Gradientenverfahrens zur Berechnung einer Regression. Wir importieren numpy und matplotlib.pyplot und erzeugen uns künstliche Datenpunkte:

import numpy as np
import matplotlib.pyplot as plt


X = 2 * np.random.rand(1000, 1)
y = 5 + 2 * X + np.random.randn(1000, 1)

plt.figure(figsize = (15, 15))
plt.plot(X, y, "b.")
plt.axis([0, 2, 0, 15])
plt.show()

Nun wollen wir einen Lernalgorithmus über das Gradientenverfahren erstellen. Im Grunde haben wir hier es bereits mit einem linear aktivierten Neuron zutun:

Bei der linearen Regression, die wir durchführen wollen, nehmen wir zwei-dimensionale Daten (wobei wir die Regression prinzipiell auch mit x-Dimensionen durchführen können, dann hätte unser Neuron weitere Eingänge). Wir empfangen einen Bias ( $w_0$ ) der stets mit einer Eingangskonstante multipliziert und somit als Wert erhalten bleibt. Der Bias ist das Alpha $\alpha$ in einer Schulmathe-tauglichen Formel wie $y = \beta \cdot x + \alpha$ .

Beta $\beta$ ist die Steigung, der Gradient, der Funktion.

Sowohl $\alpha$ als auch $\beta$ sind uns unbekannt, versuchen wir jedoch über die Betrachtung unserer Prädiktion durch Berechnung der Formel $\^y = \beta \cdot x + \alpha$ und den darauffolgenden Abgleich mit dem tatsächlichen $y$ herauszufinden. Anfangs behaupten wir beispielsweise einfach, sowohl $\beta$ als auch $\alpha$ seien $0.00$ . Folglich wird $\^y = \beta \cdot x + \alpha$ ebenfalls gleich 0.00 sein und die Fehlerfunktion (Loss Function) wird maximal sein. Dies war der erste Durchlauf des Trainings, die sogenannte erste Epoche!

Die Epochen (Durchläufe) und dazugehörige Fehlergrößen. Wenn die Fehler sinken und mit weiteren Epochen nicht mehr wesentlich besser werden, heißt es, das der Lernalogorithmus konvergiert.

Als Fehlerfunktion verwenden wir bei der Regression die MSE-Funktion (Mean Squared Error):

$MSE = \sum(\^y_i - y_i)^2$

Um diese Funktion wird sich nun alles drehen, denn diese beschreibt den Fehler und gibt uns auch die Auskunft darüber, ob wie stark und in welche Richtung sie ansteigt, so dass wir uns entgegen der Steigung bewegen können. Wer die Regeln der Ableitung im Kopf hat, weiß, dass die Ableitung der Formel leichter wird, wenn wir sie vorher auf halbe Werte runterskalieren. Da die Proportionen dabei erhalten bleiben und uns quadrierte Fehlerwerte unserem menschlichen Verstand sowieso nicht so viel sagen (unser Gehirn denkt nunmal nicht exponential), stört das nicht:

$MSE = \frac{\frac{1}{2} \cdot \sum(\^y_i - y_i)^2}{n}$

$MSE = \frac{\frac{1}{2} \cdot \sum(w^T \cdot x_i - y_i)^2}{n}$

Wenn die Mathematik der partiellen Ableitung (Ableitung einer Funktion nach jedem Gradienten) abhanden gekommen ist, bitte nochmal folgende Regeln nachschlagen, um die nachfolgende Ableitung verstehen zu können:

Allgemeine partielle Ableitung
Kettenregel

Ableitung der MSD-Funktion nach dem einen Gewicht $w$ bzw. partiell nach jedem vorhandenen $w_j$ :

$\frac{\partial}{\partial w_j}MSE = \frac{\partial}{\partial w} \frac{1}{2} \cdot \sum(\^y - y_i)^2$

$\frac{\partial}{\partial w_j}MSE = \frac{\partial}{\partial w} \frac{1}{2} \cdot \sum(w^T \cdot x_i - y_i)^2$

$\frac{\partial}{\partial w_j}MSE = \frac{2}{n} \cdot \sum(w^T \cdot x_i - y_i) \cdot x_{ij}$

Woher wir das $x_{ij}$ am Ende her haben? Das ergibt sie aus der Kettenregel: Die äußere Funktion wurde abgeleitet, so wurde aus $\frac{1}{2} \cdot \sum(w^T \cdot x_i - y_i)^2$ dann $\frac{2}{n} \cdot \sum(w^T \cdot x_i - y_i)$ . Jedoch muss im Sinne eben dieser Kettenregel auch die innere Funktion abgeleitet werden. Da wir nach $w_j$ ableiten, bleibt nur $x_ij$ erhalten.

Damit können wir arbeiten! So kompliziert ist die Formel nun auch wieder nicht: $\frac{2}{n} \cdot \sum(w^T \cdot x_i - y_i) \cdot x_{ij}$

Mit dieser Formel können wir unsere Gewichte an den Fehler anpassen: ( $f\nabla$ ist der Gradient der Funktion!)

$w_j = w_j - \nabla MSE(w_j)$

Initialisieren der Gewichtungen

Die Gewichtungen $\alpha$ und $\beta$ müssen anfänglich mit Werten initialisiert werden. In der Regression bietet es sich an, die Gewichte anfänglich mit $0.00$ zu initialisieren.

Bei vielen neuronalen Netzen, mit nicht-linearen Aktivierungsfunktionen, ist das jedoch eher ungünstig und zufällige Werte sind initial besser. Gut erprobt sind normal-verteilte Zufallswerte.

Lernrate

Nur eine Kleinigkeit haben wir bisher vergessen: Wir brauchen einen Faktor, mit dem wir anpassen. Hier wäre der Faktor 1. Das ist in der Regel viel zu groß. Dieser Faktor wird geläufig als Lernrate (Learning Rate) $\eta$ (eta) bezeichnet:

$w_j = w_j - \eta \cdot \nabla MSE(w_j)$

Die Lernrate $\eta$ ist ein Knackpunkt und der erste Parameter des Lernalgorithmus, den es anzupassen gilt, wenn das Training nicht konvergiert.

Die Lernrate $\eta$ darf nicht zu groß klein gewählt werden, da das Training sonst zu viele Epochen benötigt. Ungeduldige erhöhen die Lernrate möglicherweise aber so sehr, dass der Lernalgorithmus im Minimum der Fehlerfunktion vorbeiläuft und diesen stets überspringt. Hier würde der Algorithmus also sozusagen konvergieren, weil nicht mehr besser werden, aber das resultierende Modell wäre weit vom Optimum entfernt.

Beginnen wir mit der Implementierung als Python-Klasse:

class LinearRegressionGD(object):
    
    def __init__(self, eta = 0.0001, n_iter = 50):
        
        self.eta = eta                  # Lernrate
        self.n_iter = n_iter            # Epochen
        
    def fit(self, X, y):
        
        self.w_ = np.zeros(1 + X.shape[1]) # <- 1 für den Bias + alle weiteren Columns für die Steigungen
                                           # In diesem Beispiel self.w_ = [0.0, 0.] = [Alpha, Beta]
                                           # Dabei initialisieren wir Alpha und Beta mit 0.00-Werten
        
        self.cost_ = []                    # Cost Function (der Verlauf der Loss Function MSE)
        
        for i in range(self.n_iter):       # Für jede Epoche...
            
            output = self.predict(X)       # Die Funktion x * Beta + Alpha ausrechnen  
                                           # Batch-Verfahren, denn wir trainieren jede Epoche mit allen X-Werten

            errors = y.flatten() - output  # y_predicted - y_real

            mse = ((errors ** 2).sum() / 2.0) / len(X)  # Loss Function MSE
            
            self.cost_.append(mse)                      # Loss Function wird Teil der Cost Function
            
            self.w_[1:] += self.eta * X.T.dot(errors)   # Anpassen des Gewichts Beta (und falls es sie gäbe: aller weiteren Gewichte)
            self.w_[0] += self.eta * errors.sum()      # Anpassen des Gewichts Alpha
            
            
            #print(output)
            #print(errors)
            #print("Beta  -> ", self.w_[1:])
            #print("Alpha -> ", self.w_[0])                   
            
        return self
        
    def predict(self, X):
        return np.dot(X, self.w_[1:]) + self.w_[0]      # y = x * Beta + Alpha

Die Klasse sollte so funktionieren, bevor wir sie verwenden, sollten wir die Input-Werte standardisieren:

x_std = (X - X.mean()) / X.std()
y_std = (y - y.mean()) / y.std()

Bei diesem Beispiel mit künstlich erzeugten Werten ist das Standardisieren bzw. das Fehlen des Standardisierens zwar nicht kritisch, aber man sollte es sich zur Gewohnheit machen. Testweise es einfach mal weglassen 🙂

Kommen wir nun zum Einsatz der Klasse, die die Regression via Gradientenabstieg absolvieren soll:

lrGD = LinearRegressionGD()  # Instanziieren
lrGD.fit(x_std, y_std)       # Trainieren (das ".fit()" entspricht dem Wording von scikit-learn, ".train()" wäre mir sonst lieber :-)

Was tut diese Instanz der Klasse LinearRegressionGD nun eigentlich?

Bildlich gesprochen, legt sie eine Gerade auf den Boden des Koordinatensystems, denn die Gewichtungen werden mit 0.00 initialisiert, $y$ ist also gleich 0.00, egal welche Werte in $x$ enthalten sind. Der Fehler ist dann aber sehr groß (sollte maximal sein, im Vergleich zu zukünftigen Epochen). Die Gewichte werden also angepasst, die Gerade somit besser in die Punktwolke platziert. Mit jeder Epoche wird die Gerade erneut in die Punktwolke gelegt, der Gesamtfehler (über alle $x$ , da wir es hier mit dem Batch-Verfahren zutun haben) berechnet, die Werte angepasst… bis die vorgegebene Zahl an Epochen abgelaufen ist.

Schauen wir uns das Ergebnis des Trainings an:

plt.figure(figsize = (15, 15))
plt.plot(x_std, y_std, "b.")                                # Scatter, wie zuvor!
plt.plot(x_std, lrGD.predict(x_std), "r-", linewidth = 5)   # Regressionsgerade als Linie
plt.show()

Die Linie sieht passend aus, oder? Da wir hier nicht zu sehr in die Theorie der Regressionsanalyse abdriften möchten, lassen wir das testen und prüfen der Akkuratesse mal aus, hier möchte ich auf meinen Artikel Regressionsanalyse in Python mit Scikit-Learn verweisen.

Prüfen sollten wir hingegen mal, wie schnell der Lernalgorithmus mit der vorgegebenen Lernrate $eta$ konvergiert:

plt.figure(figsize = (15, 15))
plt.plot(range(1, lrGD.n_iter + 1), lrGD.cost_)
plt.xlabel('Epochen')
plt.ylabel('Summe quadrierter Abweichungen')
plt.show()

Hier die Verlaufskurve der Cost Function:

Die Kurve zeigt uns, dass spätestens nach 40 Epochen kaum noch Verbesserung (im Sinne der Gesamtfehler-Minimierung) erreicht wird.

Wichtige Hinweise

Natürlich war das nun nur ein erster kleiner Einstieg und wer es verstanden hat, hat viel gewonnen. Denn erst dann kann man sich vorstellen, wie ein einzelnen Neuron eines künstlichen neuronalen Netzes grundsätzlich trainiert werden kann.

Folgendes sollte noch beachtet werden:

Lernrate $\eta$ :
Die Lernrate ist ein wichtiger Parameter. Wer das Programmier-Beispiel bei sich zum Laufen gebracht hat, einfach mal die Lernrate auf Werte zwischen 10.00 und 0.00000001 setzen, schauen was passiert 🙂
Globale Minima vs lokale Minima:
Diese lineare zwei-dimensionale Regression ist ziemlich einfach. Neuronale Netze sind hingegen komplexer und haben nicht einfach nur eine simple konvexe Fehlerfunktion. Hier gibt es mehrere Hügel und Täler in der Fehlerfunktion und die Gefahr ist groß, in einem lokalen, nicht aber in einem globalen Minimum zu landen.
Stochastisches Gradientenverfahren:
Wir haben hier das sogenannte Batch-Verfahren verwendet. Dieses ist grundsätzlich besser als die stochastische Methode. Denn beim Batch verwenden wir den gesamten Stapel an $x$ -Werten für die Fehlerbestimmung. Allerdings ist dies bei großen Daten zu rechen- und speicherintensiv. Dann werden kleinere Unter-Stapel (Sub-Batches) zufällig aus den $x$ -Werten ausgewählt, der Fehler daraus bestimmt (was nicht ganz so akkurat ist, wie als würden wir den Fehler über alle $x$ berechnen) und der Gradient bestimmt. Dies ist schon Rechen- und Speicherkapazität, erfordert aber meistens mehr Epochen.

Buchempfehlung

Die folgenden zwei Bücher haben mir bei der Erstellung dieses Beispiels geholfen und kann ich als hilfreiche und deutlich weiterführende Lektüre empfehlen:


Machine Learning mit Python und Scikit-Learn und TensorFlow: Das umfassende Praxis-Handbuch für Data Science, Predictive Analytics und Deep Learning (mitp Professional)	Hands-On Machine Learning with Scikit-Learn and TensorFlow: Concepts, Tools, and Techniques for Building Intelligent Systems

Künstliche Intelligenz und Vorurteil

December 27, 2018/in Artificial Intelligence, Main Category/by David Schönleber

Kaum ein anderes technologisches Thema heutzutage wird hinsichtlich gesellschaftlicher Auswirkungen so kontrovers diskutiert wie das der Künstlichen Intelligenz (KI). Während das Wörtchen „KI“ bei den einen Zukunftsvisionen hervorruft, in welchen technologischer Fortschritt menschliche Probleme wie Hunger, Krankheit und Klimawandel reduziert hat, zeichnen andere düstere Bilder von Orwell‘schen Überwachungsstaaten und technologischen Apokalypsen.

Starke, schwache KI

Es ist die Unschärfe des Begriffes „KI“, welcher eine derart große Bandbreite an Zukunftsszenarien ermöglicht. Für diejenigen, welche sich an solch spekulativen Debatten beteiligen, beutet KI „starke KI“ – eine künstliche Intelligenz, deren intellektuellen Fähigkeiten die eines Menschen erreichen oder gar übertreffen. Und so spannend die Diskussion über starke KI auch ist – sie ist reine Spekulation. Heute existierende KI ist weit, sehr weit von starker KI entfernt. Worüber wir heutzutage verfügen ist die sogenannte „schwache KI“ – Algorithmen, die spezifische Anwendungsprobleme (z.B. Bilderkennung, Spracherkennung, Übersetzung, Go spielen) lösen können. Und das mitunter sehr viel besser als Menschen.

Wo heutzutage „KI“ draufsteht, sind innen überwiegend Algorithmen aus dem Bereich des maschinellen Lernens (allen voran Deep Learning) am Werk. Diese Algorithmen können selbständig die Vorgehensweise erlernen, die zum Beispiel nötig ist, um einen gegebenen Input (z.B. ein Bild) auf einen gegebenen Output (z.B. eine Kategorie, welche den Bildinhalt beschreibt) abzubilden. Aber selbst diese „schwache KI“ birgt beträchtliches Potential – denken wir an mögliche Verbesserungen z.B. im Bereich der Medizin, Logistik, Verkehrssicherheit oder Energie- und Ressourcennutzung! Angesichts der Chancen, heutige Prozesse und Anwendungen zu verbessern, haben wir allen Grund, dem Einsatz von KI aufgeschlossen gegenüber zu stehen. Vorausgesetzt natürlich, dass KI verantwortungsvoll, „ethisch“ und sicher eingesetzt wird.

KI auf Abwegen

Ethische Herausforderungen von KI ergeben sich dabei zum einen durch die Zielsetzung. Wie ein Hammer für den Nagel an der Wand oder für den Hinterkopf eines Gegners verwendet werden kann, kann auch KI für böse Ziele missbraucht werden. Nur, dass KI im Zweifel deutlich größeren Schaden anrichten kann als ein einfacher Hammer. Und so sollten wir angesichts der Risiken dringend international diskutieren, wie wir uns hinsichtlich militärischer Anwendungen von KI verhalten wollen.

Zum anderen dringen besonders aus den USA, in denen KI Algorithmen schon heute in deutlich größerem Ausmaß eingesetzt werden als in Deutschland, immer wieder beunruhigende Nachrichten über voreingenommene KI Algorithmen. Zum ersten fand eine Studie kürzlich heraus, dass kommerziell erhältliche Gesichtserkennungsalgorithmen für Frauen bzw. dunkelhäutige Menschen schlechter funktionieren als für Männer bzw. hellhäutige Menschen. Mit der unschönen Konsequenz, dass es z.B. bei einem Abgleich mit Verbrecherfotos bei Menschen mit dunkler Hautfarbe deutlich häufiger zu falschen Übereinstimmungen kommen kann als bei Menschen heller Hautfarbe. Zum zweiten wurde vor kurzem bekannt, dass eine experimentell von einem großen Technologiekonzern zur Bewertung von Bewerbungen verwendete KI von Frauen stammende Bewerbungen systematisch schlechter bewertete als von Männern stammende Bewerbungen.

Wie KI zu Vorurteilen kommt

Um die Ursachen für vorurteilsbehaftete KI besser zu verstehen, lohnt es sich, einen Blick hinter die Kulissen zu werfen. Denn wie jede Technologie existiert auch KI nicht im luftleeren Raum. Dies lässt sich leicht anhand der Faktoren verdeutlichen, welche zum Erfolg heutiger KI beigetragen haben: bessere Hardware, cleverere Algorithmen und größere Datenmengen. Und gerade diese Daten sind es, durch welche Vorurteile in KI Einzug halten können.

Die Vorstellung von „neutralen Daten“ ist nämlich eine Wunschvorstellung. Im besten Fall spiegeln Daten die Welt wider, in der wir leben. Eine Welt zum Beispiel, in der in Technologiekonzernen typischerweise deutlich mehr Männer beschäftigt sind als Frauen – was eine auf dem Personalbestand eines Technologiekonzerns trainierte KI dazu veranlassen kann, zu „schlussfolgern“, dass männliche Bewerber im Auswahlverfahren zu bevorzugen sind. Oder eine Welt, in der Länder bzw. gesellschaftliche Schichten innerhalb eines Landes unterschiedlichen Zugang zu modernen Technologien oder auch Bildung haben. Eine Ungleichheit, die sich als Dominanz westlicher Industrienationen in der geografischen Zusammensetzung von zum Training von KI-Algorithmen verwendeter Datensätze auswirken kann. Eine Dominanz, die wiederum zur Folge haben kann, dass derart trainierte KI-Algorithmen besonders gut für Menschen aus westlichen Industrienationen funktionieren. Ganz zu schweigen von der Voreingenommenheit der menschlichen Wahrnehmung, welche die Zusammensetzung von Daten beeinflusst – denken wir an das begrenzte Spektrum der Bilder, welche uns zuerst zu dem Begriff „Genie“ in den Sinn kommen.

Aber nicht nur die verwendeten Trainingsdaten, sondern auch bei der Entwicklung von KI getroffenen Design-Entscheidungen können negative Auswirkungen haben. Wenn bei einem nicht perfekt funktionierenden Bilderkennungsalgorithmus potentiell abwertende Kategorien zur Klassifikation zur Verfügung stehen, kann dies dazu führen, dass – wie in der Vergangenheit geschehen – dunkelhäutige Menschen als Gorillas klassifiziert werden. Wenn bei der Evaluation eines z.B. für die Gesichtserkennung eingesetzten KI-Algorithmus nur die Genauigkeit über alle Bevölkerungsgruppen hinweg berücksichtigt wird, können Ungleichheiten in der Genauigkeit nicht entdeckt werden, was zu Problemen bei der Anwendung führen kann. Denn Nutzer von KI-Algorithmen vermuten zumeist, dass die Algorithmen für alle denkbaren Anwendungszwecke geeignet sind.

Werte statt Wegsehen

Entgegen der verbreiteten Auffassung sind KI Algorithmen also nicht notwendigerweise vorurteilsfrei – sie können menschliche Voreingenommenheit bzw. gesellschaftliche Ungleichheit widerspiegeln. Da Algorithmen anders und in anderem Maß als Menschen eingesetzt werden, kann das bei blauäugiger Verwendung dazu führen, dass bestehende Ungleichheiten nicht nur bestärkt, sondern sogar vergrößert werden. Richtig angewendet können Algorithmen jedoch helfen, implizite und explizite Vorurteile menschlicher Entscheider zu mindern. Denn wie wir durch viele Studien wissen, ist die Liste der kognitiven Verzerrungen, die wir Menschen aufweisen, lang.

Es ist für den verantwortlichen Einsatz von KI in einem sensiblen Kontext somit essenziell, zu wissen, welche „ethischen“ Kriterien KI für den konkreten Anwendungsfall erfüllen muss. So kann sichergestellt werden, dass die KI den Anforderungen entspricht, bevor sie angewendet wird – oder aber, dass sie solange nicht angewendet wird, wie sie den Anforderungen nicht entspricht. Und mittels Transparenz, Überwachung und Feedback-Möglichkeiten lässt sich vermeiden, dass ein selbst-verbessernder KI-Algorithmus im Laufe der Zeit das ihm gesteckte Ziel verfehlt.

Für viele Anwendungsfälle sind derartige ethische Fragen jedoch vernachlässigbar, denken wir zum Beispiel an die Vorhersage von Maschinenausfällen oder die Extraktion strukturierter Daten aus unstrukturierten Dokumenten. Aber es ist nichtsdestotrotz gut und wichtig, Ethik und KI zusammen zu denken. Denn dies ermöglicht es uns, sicherzustellen, dass wir KI auf die bestmögliche Weise einsetzen. Denn das enorme Potential von KI gibt uns die Chance, den Status quo nachhaltig positiv zu verändern – technologisch wie ethisch.

Cloudera beschleunigt die KI-Industrialisierung mit Cloud nativer Machine-Learning-Plattform

December 6, 2018/in Sponsoring Partner Posts, Tool Introduction/by cloudera

Neues Cloudera-Angebot vereinfacht Machine-Learning-Workflows mit einer einheitlichen Erfahrung für Data Engineering und Data Science auf Kubernetes.

München, Palo Alto (Kalifornien), 5. Dezember 2018 – Cloudera, Inc. (NYSE: CLDR) hat eine Vorschau auf eine neue, Cloud-basierte Machine-Learning-Plattform der nächsten Generation auf Basis von Kubernetes veröffentlicht. Das kommende Cloudera Machine Learning erweitert das Angebot von Cloudera für Self-Service Data Science im Unternehmen. Es bietet eine schnelle Bereitstellung und automatische Skalierung sowie eine containerisierte, verteilte Verarbeitung auf heterogenen Rechnern. Cloudera Machine Learning gewährleistet auch einen sicheren Datenzugriff mit einem einheitlichen Erlebnis in lokalen, Public-Cloud- und hybriden Umgebungen.

Im Gegensatz zu Data-Science-Tools, die nur Teile des Machine-Learning-Workflows adressieren oder nur für die Public Cloud verfügbar sind, kombiniert Cloudera Machine Learning Data Engineering und Data Science, auf beliebigen Daten und überall. Darüber hinaus werden Datensilos aufgelöst, um den kompletten Machine-Learning-Workflow zu vereinfachen und zu beschleunigen. Unternehmen können ab sofort hier Zugang zu einer Vorabversion von Cloudera Machine Learning anfragen.

Container und das Kubernetes-Ökosystem ermöglichen die Agilität der Cloud in verschiedenen Umgebungen mit einer konsistenten Erfahrung und ermöglichen die Bereitstellung skalierbarer Services für die IT in hybriden und Multi-Cloud-Implementierungen. Gleichzeitig sind Unternehmen bestrebt, komplette Machine-Learning-Workflows zu operationalisieren und zu skalieren. Mit Cloudera Machine Learning können Unternehmen Machine Learning von der Forschung bis zur Produktion beschleunigen. Benutzer sind in der Lage, Umgebungen einfach bereitzustellen und Ressourcen zu skalieren und müssen so weniger Zeit für die Infrastruktur und können mehr Zeit für Innovationen aufwenden.

Zu den Fähigkeiten gehören:

Nahtlose Portierbarkeit über Private Cloud, Public Cloud und Hybrid Cloud auf Basis von Kubernetes.
Schnelle Cloud-Bereitstellung und automatische Skalierung.
Skalierbares Data Engineering und Machine Learning mit nahtloser Abhängigkeitsverwaltung durch containerisiertes Python, R und Spark-on-Kubernetes.
Hochgeschwindigkeits-Deep-Learning mit verteiltem GPU-Scheduling und Training.
Sicherer Datenzugriff über HDFS, Cloud Object Stores und externe Datenbanken hinweg.

„Teams produktiver zu machen, ist entscheidend für die Skalierung von Machine Learning im Unternehmen. Modelle konsistent über eine hochskalierbare, transparente Infrastruktur zu erstellen und einzusetzen und dabei überall auf Daten zuzugreifen, erfordert aber eine neuartige Plattform”, sagt Hilary Mason, General Manager, Machine Learning bei Cloudera. „Cloudera Machine Learning vereint die kritischen Funktionen von Data Engineering, kollaborativer Exploration, Modelltraining und -bereitstellung in einer Cloud-basierten Plattform, die dort läuft, wo Sie sie benötigen – mit den integrierten Sicherheits-, Governance- und Managementfunktionen, die unsere Kunden nachfragen.”

„Bei Akamai haben wir ausgereifte Web-Sicherheitssysteme auf der Grundlage einer umfassenden Datenanalyse und -verarbeitung aufgebaut. Dabei ist uns bewusst geworden, dass Geschwindigkeit und Skalierbarkeit entscheidend für die Erkennung von Anomalien im Internet sind”, sagt Oren Marmor, DevOps Manager, Web Security bei Akamai. „Die Agilität, die Docker und Kubernetes Apache Spark verleihen, ist für uns ein wichtiger Baustein, sowohl für Data Science als auch für Data Engineering. Wir freuen uns sehr über die Einführung der kommenden Cloudera Machine Learning Plattform. Die Möglichkeit, mit der Plattform das Abhängigkeitsmanagement von Betriebssystemen und Bibliotheken zu vereinfachen, ist eine vielversprechende Entwicklung.”

Matt Brandwein, Senior Director of Products bei Cloudera, erläutert im Video, wie die neue Cloudera Plattform Teams in die Lage versetzt, Machine Learning im Unternehmen zu entwickeln und einzusetzen.

Mit Cloudera Machine Learning sowie der Forschung und fachkundigen Beratung durch die Cloudera Fast Forward Labs bietet Cloudera einen umfassenden Ansatz zur Beschleunigung der Industrialisierung von KI.

Um Kunden dabei zu unterstützen, KI überall zu nutzen, hat das Applied Research Team von Cloudera kürzlich Federated Learning eingeführt, um Machine-Learning-Modelle von der Cloud bis zum Edge einzusetzen, gleichzeitig den Datenschutz zu gewährleisten und den Aufwand für die Netzwerkkommunikation zu reduzieren. Der Bericht bietet eine detaillierte, technische Erläuterung des Ansatzes sowie praktische technische Empfehlungen, die sich mit Anwendungsfällen in den Bereichen Mobilfunk, Gesundheitswesen und Fertigung befassen, einschließlich IoT-gesteuerter Predictive Maintenance.

„Federated Learning beseitigt Hindernisse für die Anwendung von Machine Learning in stark regulierten und wettbewerbsorientierten Branchen. Wir freuen uns sehr, unseren Kunden helfen zu können, damit Starthilfe für die Industrialisierung der KI zu erhalten”, so Mike Lee Williams, Forschungsingenieur bei Cloudera Fast Forward Labs.

Mike Lee Williams, Research Engineer bei den Cloudera Fast Forward Labs, erklärt im Video, wie Machine-Learning-Systeme mit Hilfe von Federated Learning ohne direkten Zugriff auf Trainingsdaten aufgebaut werden können.

Über Cloudera

Bei Cloudera glauben wir, dass Daten morgen Dinge ermöglichen werden, die heute noch unmöglich sind. Wir versetzen Menschen in die Lage, komplexe Daten in klare, umsetzbare Erkenntnisse zu transformieren. Wir sind die moderne Plattform für Machine Learning und Analysen, optimiert für die Cloud. Die größten Unternehmen der Welt vertrauen Cloudera bei der Lösung ihrer herausforderndsten, geschäftlichen Probleme. Weitere Informationen finden Sie unter de.cloudera.com/.