Aika: Ein semantisches neuronales Netzwerk
Wenn es darum geht Informationen aus natürlichsprachigen Texten zu extrahieren, stehen einem verschiedene Möglichkeiten zur Verfügung. Eine der ältesten und wohl auch am häufigsten genutzten Möglichkeiten ist die der regulären Ausdrücke. Hier werden exakte Muster definiert und in einem Textstring gematcht. Probleme bereiten diese allerdings, wenn kompliziertere semantische Muster gefunden werden sollen oder wenn verschiedene Muster aufeinander aufbauen oder miteinander interagieren sollen. Gerade das ist aber der Normalfall bei der Verarbeitung von natürlichem Text. Muster hängen voneinander ab, verstärken oder unterdrücken sich gegenseitig.
Prädestiniert um solche Beziehungen abzubilden wären eigentlich künstliche neuronale Netze. Diese haben nur das große Manko, dass sie keine strukturierten Informationen verarbeiten können. Neuronale Netze bringen von sich aus keine Möglichkeit mit, die relationalen Beziehungen zwischen Worten oder Phrasen zu verarbeiten. Ein weiteres Problem neuronaler Netze ist die Verarbeitung von Feedback-Schleifen, bei denen einzelne Neuronen von sich selbst abhängig sind. Genau diese Probleme versucht der Aika Algorithmus (www.aika-software.org) zu lösen.
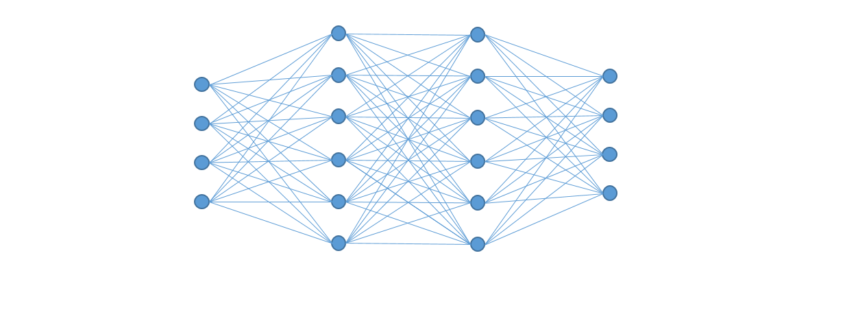
Der Aika Algorithmus ist als Open Source Java-Bibliothek implementiert und dient dazu semantische Informationen in Texten zu erkennen und zu verarbeiten. Da semantische Informationen sehr häufig mehrdeutig sind, erzeugt die Bibliothek für jede dieser Bedeutungen eine eigene Interpretation und wählt zum Schluss die am höchsten gewichtete aus. Aika kombiniert dazu aktuelle Ideen und Konzepte aus den Bereichen des maschinellen Lernens und der künstlichen Intelligenz, wie etwa künstliche neuronale Netze, Frequent Pattern Mining und die auf formaler Logik basierenden Expertensysteme. Aika basiert auf der heute gängigen Architektur eines künstlichen neuronalen Netzwerks (KNN) und nutzt diese, um sprachliche Regeln und semantische Beziehungen abzubilden.
Die Knackpunkte: relationale Struktur und zyklische Abhängigkeiten
Das erste Problem: Texte haben eine von Grund auf relationale Struktur. Die einzelnen Worte stehen über ihre Reihenfolge in einer ganz bestimmten Beziehung zueinander. Gängige Methoden, um Texte für die Eingabe in ein KNN auszuflachen, sind beispielsweise Bag-of-Words oder Sliding-Window. Mittlerweile haben sich auch rekurrente neuronale Netze etabliert, die das gesamte Netz in einer Schleife für jedes Wort des Textes mehrfach hintereinander schalten. Aika geht hier allerdings einen anderen Weg. Aika propagiert die relationalen Informationen, also den Textbereich und die Wortposition, gemeinsam mit den Aktivierungen durch das Netzwerk. Die gesamte relationale Struktur des Textes bleibt also erhalten und lässt sich jederzeit zur weiteren Verarbeitung nutzen.
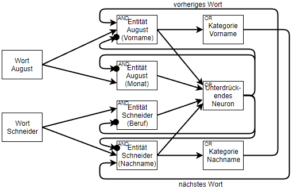
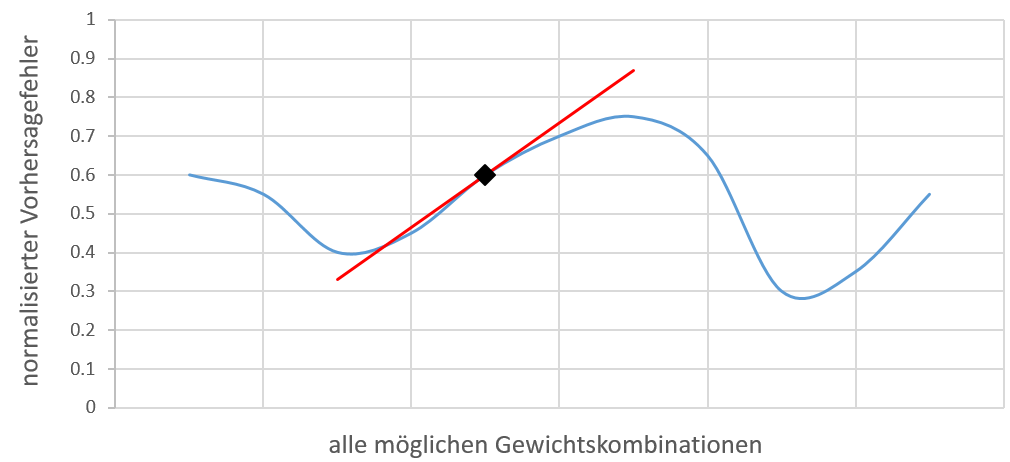
Das zweite Problem ist, dass bei der Verarbeitung von Text häufig nicht klar ist, in welcher Reihenfolge einzelne Informationen verarbeitet werden müssen. Wenn wir beispielsweise den Namen „August Schneider“ betrachten, können sowohl der Vor- als auch der Nachname in einem anderen Zusammenhang eine völlig andere Bedeutung annehmen. August könnte sich auch auf den Monat beziehen. Und genauso könnte Schneider eben auch den Beruf des Schneiders meinen. Einfache Regeln, um hier dennoch den Vor- und den Nachnamen zu erkennen, wären: „Wenn das nachfolgende Wort ein Nachname ist, handelt es sich bei August um einen Vornamen“ und „Wenn das vorherige Wort ein Vorname ist, dann handelt es sich bei Schneider um einen Nachnamen“. Das Problem dabei ist nur, dass unsere Regeln nun eine zyklische Abhängigkeit beinhalten. Aber ist das wirklich so schlimm? Aika erlaubt es, genau solche Feedback-Schleifen abzubilden. Wobei die Schleifen sowohl positive, als auch negative Gewichte haben können. Negative rekurrente Synapsen führen dazu, dass zwei sich gegenseitig ausschließende Interpretationen entstehen. Der Trick ist nun zunächst nur Annahmen zu treffen, also etwa dass es sich bei dem Wort „Schneider“ um den Beruf handelt und zu schauen wie das Netzwerk auf diese Annahme reagiert. Es bedarf also einer Evaluationsfunktion und einer Suche, die die Annahmen immer weiter variiert, bis schließlich eine optimale Interpretation des Textes gefunden ist. Genau wie schon der Textbereich und die Wortposition werden nun auch die Annahmen gemeinsam mit den Aktivierungen durch das Netzwerk propagiert.
Die zwei Ebenen des Aika Algorithmus
Aber wie lassen sich diese Informationen mit den Aktivierungen durch das Netzwerk propagieren, wo doch der Aktivierungswert eines Neurons für gewöhnlich nur eine Fließkommazahl ist? Genau hier liegt der Grund, weshalb Aika unter der neuronalen Ebene mit ihren Neuronen und kontinuierlich gewichteten Synapsen noch eine diskrete Ebene besitzt, in der es eine Darstellung aller Neuronen in boolscher Logik gibt. Aika verwendet als Aktivierungsfunktion die obere Hälfte der Tanh-Funktion. Alle negativen Werte werden auf 0 gesetzt und führen zu keiner Aktivierung des Neurons. Es gibt also einen klaren Schwellenwert, der zwischen aktiven und inaktiven Neuronen unterscheidet. Anhand dieses Schwellenwertes lassen sich die Gewichte der einzelnen Synapsen in boolsche Logik übersetzen und entlang der Gatter dieser Logik kann nun ein Aktivierungsobjekt mit den Informationen durch das Netzwerk propagiert werden. So verbindet Aika seine diskrete bzw. symbolische Ebene mit seiner subsymbolischen Ebene aus kontinuierlichen Synapsen-Gewichten.
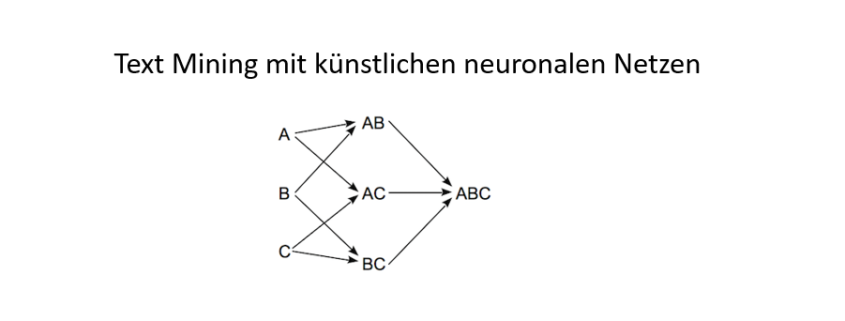
Die Logik Ebene in Aika erlaubt außerdem einen enormen Effizienzgewinn im Vergleich zu einem herkömmlichen KNN, da die gewichtete Summe von Neuronen nur noch für solche Neuronen berechnet werden muss, die vorher durch die Logikebene aktiviert wurden. Im Falle eines UND-verknüpfenden Neurons bedeutet das, dass das Aktivierungsobjekt zunächst mehrere Ebenen einer Lattice-Datenstruktur aus UND-Knoten durchlaufen muss, bevor das eigentliche Neuron berechnet und aktiviert werden kann. Diese Lattice-Datenstruktur stammt aus dem Bereich des Frequent Pattern Mining und enthält in einem gerichteten azyklischen Graphen alle Teilmuster eines beliebigen größeren Musters. Ein solches Frequent Pattern Lattice kann in zwei Richtungen betrieben werden. Zum Einen können damit bereits bekannte Muster gematcht werden, und zum Anderen können auch völlig neue Muster damit erzeugt werden.
Da es schwierig ist Netze mit Millionen von Neuronen im Speicher zu halten, nutzt Aika das Provider Architekturpattern um selten verwendete Neuronen oder Logikknoten in einen externen Datenspeicher (z.B. eine Mongo DB) auszulagern, und bei Bedarf nachzuladen.
Ein Beispielneuron
Hier soll nun noch beispielhaft gezeigt werden wie ein Neuron innerhalb des semantischen Netzes angelegt werden kann. Zu beachten ist, dass Neuronen sowohl UND- als auch ODER-Verknüpfungen abbilden können. Das Verhalten hängt dabei alleine vom gewählten Bias ab. Liegt der Bias bei 0.0 oder einem nur schwach negativen Wert reicht schon die Aktivierung eines positiven Inputs aus um auch das aktuelle Neuron zu aktivieren. Es handelt sich dann um eine ODER-Verknüpfung. Liegt der Bias hingegen tiefer im negativen Bereich dann müssen mitunter mehrere positive Inputs gleichzeitig aktiviert werden damit das aktuelle Neuron dann auch aktiv wird. Jetzt handelt es sich dann um eine UND-Verknüpfung. Der Bias Wert kann der initNeuron einfach als Parameter übergeben werden. Um jedoch die Berechnung des Bias zu erleichtern bietet Aika bei den Inputs noch den Parameter BiasDelta an. Der Parameter BiasDelta nimmt einen Wert zwischen 0.0 und 1.0 entgegen. Bei 0.0 wirkt sich der Parameter gar nicht aus. Bei einem höheren Wert hingegen wird er mit dem Betrag des Synapsengewichts multipliziert und von dem Bias abgezogen. Der Gesamtbias lautet in diesem Beispiel also -55.0. Die beiden positiven Eingabesynapsen müssen also aktiviert werden und die negative Eingabesynapse darf nicht aktiviert werden, damit dieses Neuron selber aktiv werden kann. Das Zusammenspiel von Bias und Synpasengewichten ist aber nicht nur für die Aktivierung eines Neurons wichtig, sondern auch für die spätere Auswahl der finalen Interpretation. Je stärker die Aktivierungen innerhalb einer Interpretation aktiv sind, desto höher wird diese Interpretation gewichtet.
Um eine beliebige Graphstruktur abbilden zu können, trennt Aika das Anlegen der Neuronen von der Verknüpfung mit anderen Neuronen. Mit createNeuron(“E-Schneider (Nachname)”) wird also zunächst einmal ein unverknüpftes Neuron erzeugt, das dann über die initNeuron Funktion mit den Eingabeneuronen wortSchneiderNeuron, kategorieVornameNeuron und unterdrueckendesNeuron verknüpft wird. Über den Parameter RelativeRid wird hier angegeben auf welche relative Wortposition sich die Eingabesynapse bezieht. Die Eingabesynpase zu der Kategorie Vorname bezieht sich also mit -1 auf die vorherige Wortposition. Der Parameter Recurrent gibt an ob es sich bei dieser Synpase um eine Feedback-Schleife handelt. Über den Parameter RangeMatch wird angegeben wie sich der Textbereich, also die Start- und die Endposition zwischen der Eingabe- und der Ausgabeaktivierung verhält. Bei EQUALS sollen die Bereiche also genau übereinstimmen, bei CONTAINED_IN reicht es hingegen wenn der Bereich der Eingabeaktivierung innerhalb des Bereichs der Ausgabeaktivierung liegt. Dann kann noch über den Parameter RangeOutput angegeben werden, dass der Bereich der Eingabeaktivierung an die Ausgabeaktivierung weiterpropagiert werden soll.
Neuron entitaetSchneiderNachnameNeuron = m.initNeuron(
m.createNeuron("E-Schneider (Nachname)"),
5.0,
new Input()
.setNeuron(wortSchneiderNeuron)
.setWeight(10.0f)
.setBiasDelta(1.0)
.setRelativeRid(0)
.setRecurrent(false)
.setRangeMatch(EQUALS)
.setRangeOutput(true),
new Input()
.setNeuron(kategorieVornameNeuron)
.setWeight(10.0f)
.setBiasDelta(1.0)
.setRelativeRid(-1)
.setRecurrent(true)
.setRangeMatch(NONE),
new Input()
.setNeuron(unterdrueckendesNeuron)
.setWeight(-40.0f)
.setBiasDelta(1.0)
.setRecurrent(true)
.setRangeMatch(CONTAINED_IN)
);
Fazit
Mit Aika können sehr flexibel umfangreiche semantische Modelle erzeugt und verarbeitet werden. Aus Begriffslisten verschiedener Kategorien, wie etwa: Vor- und Nachnamen, Orten, Berufen, Strassen, grammatikalischen Worttypen usw. können automatisch Neuronen generiert werden. Diese können dann dazu genutzt werden, Worte und Phrasen zu erkennen, einzelnen Begriffen eine Bedeutung zuzuordnen oder die Kategorie eines Begriffs zu bestimmen. Falls in dem zu verarbeitenden Text mehrdeutige Begriffe oder Phrasen auftauchen, kann Aika für diese jeweils eigene Interpretationen erzeugen und gewichten. Die sinnvollste Interpretation wird dann als Ergebnis zurück geliefert.
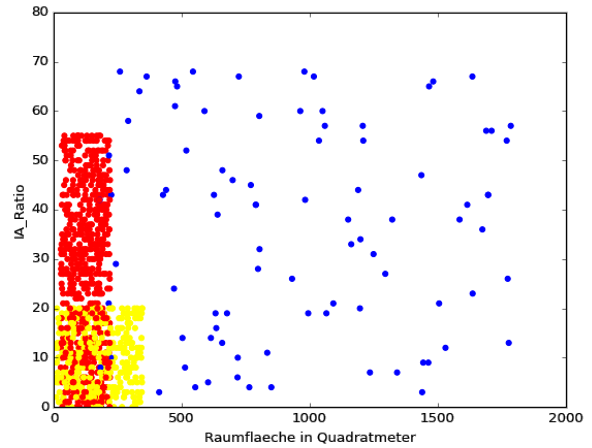
![3D Scatter Plot in Python [Matplotlib]](https://data-science-blog.com/de/wp-content/uploads/sites/5/2016/04/3d-scatter-plot-immobilien-klassifikation-gap.jpg)
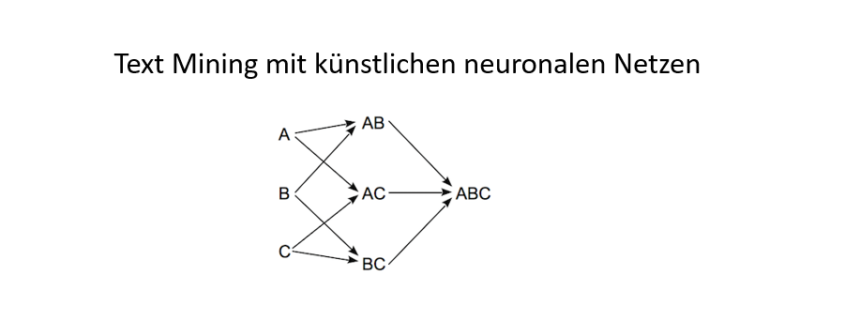
ndgedanke dabei ist es, dass Neuronen entsprechend höher gewichtet werden sollten, wenn sie mit anderen hoch gewichteten Neuronen in Beziehung stehen. Wenn also beispielsweise eine Silbe in vielen hoch gewichteten Worten auftaucht, wird sie selbst entsprechend höher gewichtet.
(Theta) multipliziert und die Ergebnisse aufsummiert. Das Zwischenergebnis ist die Aktivierungsstärke z:
