Training eines Neurons mit dem Gradientenverfahren
Dies ist Artikel 3 von 6 der Artikelserie –Einstieg in Deep Learning.
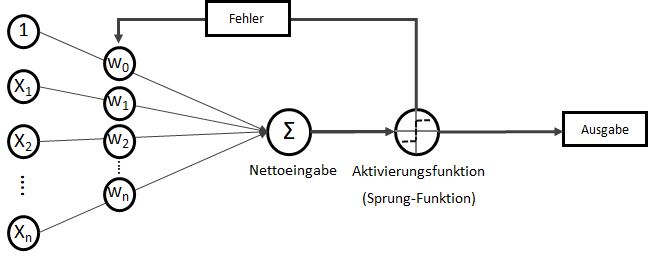
Das Training von neuronalen Netzen erfolgt nach der Forward-Propagation über zwei Schritte:
- Fehler-Rückführung über aller aktiver Neuronen aller Netz-Schichten, so dass jedes Neuron “seinen” Einfluss auf den Ausgabefehler kennt.
- Anpassung der Gewichte entgegen den Gradienten der Fehlerfunktion
Beide Schritte werden in der Regel zusammen als Backpropagation bezeichnet. Machen wir erstmal einen Schritt vor und betrachten wir, wie ein Neuron seine Gewichtsverbindungen zu seinen Vorgängern anpasst.
Gradientenabstiegsverfahren
Der Gradientenabstieg ist ein generalisierbarer Algorithmus zur Optimierung, der in vielen Verfahren des maschinellen Lernens zur Anwendung kommt, jedoch ganz besonders als sogenannte Backpropagation im Deep Learning den Erfolg der künstlichen neuronalen Netze erst möglich machen konnte.
Der Gradientenabstieg lässt sich vom Prinzip her leicht erklären: Angenommen, man stünde im Gebirge im dichten Nebel. Das Tal, und somit der Weg nach Hause, ist vom Nebel verdeckt. Wohin laufen wir? Wir können das Ziel zwar nicht sehen, tasten uns jedoch so heran, dass unser Gehirn den Gradienten (den Unterschied der Höhen beider Füße) berechnet, somit die Steigung des Bodens kennt und sich entgegen dieser Steigung unser Weg fortsetzt.
Konkret funktioniert der Gradientenabstieg so: Wir starten bei einem zufälligen Theta ![]() (Random Initialization). Wir berechnen die Ausgabe (Forwardpropogation) und vergleichen sie über eine Verlustfunktion (z. B. über die Funktion Mean Squared Error) mit dem tatsächlich korrekten Wert. Auf Grund der zufälligen Initialisierung haben wir eine nahe zu garantierte Falschheit der Ergebnisse und somit einen Verlust. Für die Verlustfunktion berechnen wir den Gradienten für gegebene Eingabewerte. Voraussetzung dafür ist, dass die Funktion ableitbar ist. Wir bewegen uns entgegen des Gradienten in Richtung Minimum der Verlustfunktion. Ist dieses Minimum (fast) gefunden, spricht man auch davon, dass der Lernalgorithmus konvergiert.
(Random Initialization). Wir berechnen die Ausgabe (Forwardpropogation) und vergleichen sie über eine Verlustfunktion (z. B. über die Funktion Mean Squared Error) mit dem tatsächlich korrekten Wert. Auf Grund der zufälligen Initialisierung haben wir eine nahe zu garantierte Falschheit der Ergebnisse und somit einen Verlust. Für die Verlustfunktion berechnen wir den Gradienten für gegebene Eingabewerte. Voraussetzung dafür ist, dass die Funktion ableitbar ist. Wir bewegen uns entgegen des Gradienten in Richtung Minimum der Verlustfunktion. Ist dieses Minimum (fast) gefunden, spricht man auch davon, dass der Lernalgorithmus konvergiert.
Das Gradientenabstiegsverfahren ist eine Möglichkeit der Gradientenverfahren, denn wollten wir maximieren, würden wir uns entlang des Gradienten bewegen, was in anderen Anwendungen sinnvoll ist.
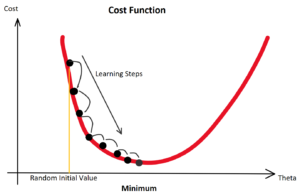
Ob als “Cost Function” oder als “Loss Function” bezeichnet, in jedem Fall ist es eine “Error Function”, aber auf die Benennung kommen wir später zu sprechen. Jedenfalls versuchen wir die Fehlerrate zu senken! Leider sind diese Funktionen in der Praxis selten so einfach konvex (zwei Berge mit einem Tal dazwischen).
Aber Achtung: Denn befinden wir uns nur zwischen zwei Bergen, finden wir das Tal mit Sicherheit über den Gradienten. Befinden wir uns jedoch in einem richtigen Gebirge mit vielen Bergen und Tälern, gilt es, das richtige Tal zu finden. Bei der Optimierung der Gewichtungen von künstlichen neuronalen Netzen wollen wir die besten Gewichtungen finden, die uns zu den geringsten Ausgaben der Verlustfunktion führen. Wir suchen also das globale Minimum unter den vielen (lokalen) Minima.
Programmier-Beispiel in Python
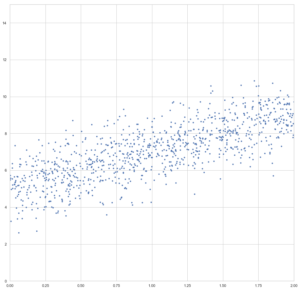
Nachfolgend ein Beispiel des Gradientenverfahrens zur Berechnung einer Regression. Wir importieren numpy und matplotlib.pyplot und erzeugen uns künstliche Datenpunkte:
import numpy as np import matplotlib.pyplot as plt X = 2 * np.random.rand(1000, 1) y = 5 + 2 * X + np.random.randn(1000, 1) plt.figure(figsize = (15, 15)) plt.plot(X, y, "b.") plt.axis([0, 2, 0, 15]) plt.show()
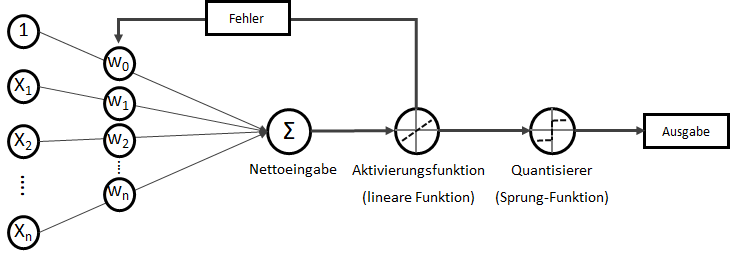
Nun wollen wir einen Lernalgorithmus über das Gradientenverfahren erstellen. Im Grunde haben wir hier es bereits mit einem linear aktivierten Neuron zutun:
Bei der linearen Regression, die wir durchführen wollen, nehmen wir zwei-dimensionale Daten (wobei wir die Regression prinzipiell auch mit x-Dimensionen durchführen können, dann hätte unser Neuron weitere Eingänge). Wir empfangen einen Bias (![]() ) der stets mit einer Eingangskonstante multipliziert und somit als Wert erhalten bleibt. Der Bias ist das Alpha
) der stets mit einer Eingangskonstante multipliziert und somit als Wert erhalten bleibt. Der Bias ist das Alpha ![]() in einer Schulmathe-tauglichen Formel wie
in einer Schulmathe-tauglichen Formel wie ![]() .
.
Beta ![]() ist die Steigung, der Gradient, der Funktion.
ist die Steigung, der Gradient, der Funktion.
Sowohl ![]() als auch
als auch ![]() sind uns unbekannt, versuchen wir jedoch über die Betrachtung unserer Prädiktion durch Berechnung der Formel
sind uns unbekannt, versuchen wir jedoch über die Betrachtung unserer Prädiktion durch Berechnung der Formel ![]() und den darauffolgenden Abgleich mit dem tatsächlichen
und den darauffolgenden Abgleich mit dem tatsächlichen ![]() herauszufinden. Anfangs behaupten wir beispielsweise einfach, sowohl
herauszufinden. Anfangs behaupten wir beispielsweise einfach, sowohl ![]() als auch
als auch ![]() seien
seien ![]() . Folglich wird
. Folglich wird ![]() ebenfalls gleich 0.00 sein und die Fehlerfunktion (Loss Function) wird maximal sein. Dies war der erste Durchlauf des Trainings, die sogenannte erste Epoche!
ebenfalls gleich 0.00 sein und die Fehlerfunktion (Loss Function) wird maximal sein. Dies war der erste Durchlauf des Trainings, die sogenannte erste Epoche!
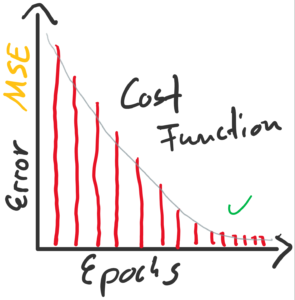
Die Epochen (Durchläufe) und dazugehörige Fehlergrößen. Wenn die Fehler sinken und mit weiteren Epochen nicht mehr wesentlich besser werden, heißt es, das der Lernalogorithmus konvergiert.
Als Fehlerfunktion verwenden wir bei der Regression die MSE-Funktion (Mean Squared Error):
![]()
Um diese Funktion wird sich nun alles drehen, denn diese beschreibt den Fehler und gibt uns auch die Auskunft darüber, ob wie stark und in welche Richtung sie ansteigt, so dass wir uns entgegen der Steigung bewegen können. Wer die Regeln der Ableitung im Kopf hat, weiß, dass die Ableitung der Formel leichter wird, wenn wir sie vorher auf halbe Werte runterskalieren. Da die Proportionen dabei erhalten bleiben und uns quadrierte Fehlerwerte unserem menschlichen Verstand sowieso nicht so viel sagen (unser Gehirn denkt nunmal nicht exponential), stört das nicht:
![]()
![]()
Wenn die Mathematik der partiellen Ableitung (Ableitung einer Funktion nach jedem Gradienten) abhanden gekommen ist, bitte nochmal folgende Regeln nachschlagen, um die nachfolgende Ableitung verstehen zu können:
- Allgemeine partielle Ableitung
- Kettenregel
Ableitung der MSD-Funktion nach dem einen Gewicht ![]() bzw. partiell nach jedem vorhandenen
bzw. partiell nach jedem vorhandenen ![]() :
:
![]()
![]()
![]()
Woher wir das ![]() am Ende her haben? Das ergibt sie aus der Kettenregel: Die äußere Funktion wurde abgeleitet, so wurde aus
am Ende her haben? Das ergibt sie aus der Kettenregel: Die äußere Funktion wurde abgeleitet, so wurde aus ![]() dann
dann ![]() . Jedoch muss im Sinne eben dieser Kettenregel auch die innere Funktion abgeleitet werden. Da wir nach
. Jedoch muss im Sinne eben dieser Kettenregel auch die innere Funktion abgeleitet werden. Da wir nach ![]() ableiten, bleibt nur
ableiten, bleibt nur ![]() erhalten.
erhalten.
Damit können wir arbeiten! So kompliziert ist die Formel nun auch wieder nicht: ![]()
Mit dieser Formel können wir unsere Gewichte an den Fehler anpassen: (![]() ist der Gradient der Funktion!)
ist der Gradient der Funktion!)
![]()
Initialisieren der Gewichtungen
Die Gewichtungen ![]() und
und ![]() müssen anfänglich mit Werten initialisiert werden. In der Regression bietet es sich an, die Gewichte anfänglich mit
müssen anfänglich mit Werten initialisiert werden. In der Regression bietet es sich an, die Gewichte anfänglich mit ![]() zu initialisieren.
zu initialisieren.
Bei vielen neuronalen Netzen, mit nicht-linearen Aktivierungsfunktionen, ist das jedoch eher ungünstig und zufällige Werte sind initial besser. Gut erprobt sind normal-verteilte Zufallswerte.
Lernrate
Nur eine Kleinigkeit haben wir bisher vergessen: Wir brauchen einen Faktor, mit dem wir anpassen. Hier wäre der Faktor 1. Das ist in der Regel viel zu groß. Dieser Faktor wird geläufig als Lernrate (Learning Rate) ![]() (eta) bezeichnet:
(eta) bezeichnet:
![]()
Die Lernrate ![]() ist ein Knackpunkt und der erste Parameter des Lernalgorithmus, den es anzupassen gilt, wenn das Training nicht konvergiert.
ist ein Knackpunkt und der erste Parameter des Lernalgorithmus, den es anzupassen gilt, wenn das Training nicht konvergiert.
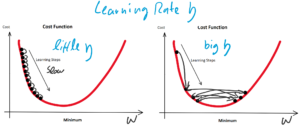
Die Lernrate ![]() darf nicht zu groß klein gewählt werden, da das Training sonst zu viele Epochen benötigt. Ungeduldige erhöhen die Lernrate möglicherweise aber so sehr, dass der Lernalgorithmus im Minimum der Fehlerfunktion vorbeiläuft und diesen stets überspringt. Hier würde der Algorithmus also sozusagen konvergieren, weil nicht mehr besser werden, aber das resultierende Modell wäre weit vom Optimum entfernt.
darf nicht zu groß klein gewählt werden, da das Training sonst zu viele Epochen benötigt. Ungeduldige erhöhen die Lernrate möglicherweise aber so sehr, dass der Lernalgorithmus im Minimum der Fehlerfunktion vorbeiläuft und diesen stets überspringt. Hier würde der Algorithmus also sozusagen konvergieren, weil nicht mehr besser werden, aber das resultierende Modell wäre weit vom Optimum entfernt.
Beginnen wir mit der Implementierung als Python-Klasse:
class LinearRegressionGD(object):
def __init__(self, eta = 0.0001, n_iter = 50):
self.eta = eta # Lernrate
self.n_iter = n_iter # Epochen
def fit(self, X, y):
self.w_ = np.zeros(1 + X.shape[1]) # <- 1 für den Bias + alle weiteren Columns für die Steigungen
# In diesem Beispiel self.w_ = [0.0, 0.] = [Alpha, Beta]
# Dabei initialisieren wir Alpha und Beta mit 0.00-Werten
self.cost_ = [] # Cost Function (der Verlauf der Loss Function MSE)
for i in range(self.n_iter): # Für jede Epoche...
output = self.predict(X) # Die Funktion x * Beta + Alpha ausrechnen
# Batch-Verfahren, denn wir trainieren jede Epoche mit allen X-Werten
errors = y.flatten() - output # y_predicted - y_real
mse = ((errors ** 2).sum() / 2.0) / len(X) # Loss Function MSE
self.cost_.append(mse) # Loss Function wird Teil der Cost Function
self.w_[1:] += self.eta * X.T.dot(errors) # Anpassen des Gewichts Beta (und falls es sie gäbe: aller weiteren Gewichte)
self.w_[0] += self.eta * errors.sum() # Anpassen des Gewichts Alpha
#print(output)
#print(errors)
#print("Beta -> ", self.w_[1:])
#print("Alpha -> ", self.w_[0])
return self
def predict(self, X):
return np.dot(X, self.w_[1:]) + self.w_[0] # y = x * Beta + Alpha
Die Klasse sollte so funktionieren, bevor wir sie verwenden, sollten wir die Input-Werte standardisieren:
x_std = (X - X.mean()) / X.std() y_std = (y - y.mean()) / y.std()
Bei diesem Beispiel mit künstlich erzeugten Werten ist das Standardisieren bzw. das Fehlen des Standardisierens zwar nicht kritisch, aber man sollte es sich zur Gewohnheit machen. Testweise es einfach mal weglassen 🙂
Kommen wir nun zum Einsatz der Klasse, die die Regression via Gradientenabstieg absolvieren soll:
lrGD = LinearRegressionGD() # Instanziieren lrGD.fit(x_std, y_std) # Trainieren (das ".fit()" entspricht dem Wording von scikit-learn, ".train()" wäre mir sonst lieber :-)
Was tut diese Instanz der Klasse LinearRegressionGD nun eigentlich?
Bildlich gesprochen, legt sie eine Gerade auf den Boden des Koordinatensystems, denn die Gewichtungen werden mit 0.00 initialisiert, ![]() ist also gleich 0.00, egal welche Werte in
ist also gleich 0.00, egal welche Werte in ![]() enthalten sind. Der Fehler ist dann aber sehr groß (sollte maximal sein, im Vergleich zu zukünftigen Epochen). Die Gewichte werden also angepasst, die Gerade somit besser in die Punktwolke platziert. Mit jeder Epoche wird die Gerade erneut in die Punktwolke gelegt, der Gesamtfehler (über alle
enthalten sind. Der Fehler ist dann aber sehr groß (sollte maximal sein, im Vergleich zu zukünftigen Epochen). Die Gewichte werden also angepasst, die Gerade somit besser in die Punktwolke platziert. Mit jeder Epoche wird die Gerade erneut in die Punktwolke gelegt, der Gesamtfehler (über alle ![]() , da wir es hier mit dem Batch-Verfahren zutun haben) berechnet, die Werte angepasst… bis die vorgegebene Zahl an Epochen abgelaufen ist.
, da wir es hier mit dem Batch-Verfahren zutun haben) berechnet, die Werte angepasst… bis die vorgegebene Zahl an Epochen abgelaufen ist.
Schauen wir uns das Ergebnis des Trainings an:
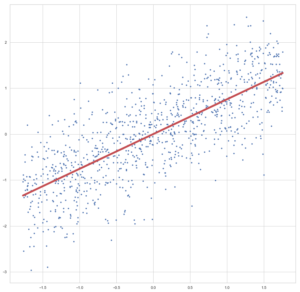
plt.figure(figsize = (15, 15)) plt.plot(x_std, y_std, "b.") # Scatter, wie zuvor! plt.plot(x_std, lrGD.predict(x_std), "r-", linewidth = 5) # Regressionsgerade als Linie plt.show()
Die Linie sieht passend aus, oder? Da wir hier nicht zu sehr in die Theorie der Regressionsanalyse abdriften möchten, lassen wir das testen und prüfen der Akkuratesse mal aus, hier möchte ich auf meinen Artikel Regressionsanalyse in Python mit Scikit-Learn verweisen.
Prüfen sollten wir hingegen mal, wie schnell der Lernalgorithmus mit der vorgegebenen Lernrate ![]() konvergiert:
konvergiert:
plt.figure(figsize = (15, 15))
plt.plot(range(1, lrGD.n_iter + 1), lrGD.cost_)
plt.xlabel('Epochen')
plt.ylabel('Summe quadrierter Abweichungen')
plt.show()
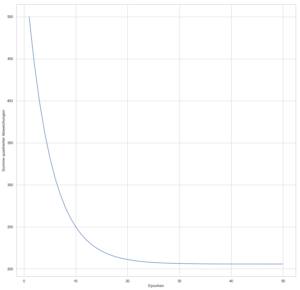
Hier die Verlaufskurve der Cost Function:
Die Kurve zeigt uns, dass spätestens nach 40 Epochen kaum noch Verbesserung (im Sinne der Gesamtfehler-Minimierung) erreicht wird.
Wichtige Hinweise
Natürlich war das nun nur ein erster kleiner Einstieg und wer es verstanden hat, hat viel gewonnen. Denn erst dann kann man sich vorstellen, wie ein einzelnen Neuron eines künstlichen neuronalen Netzes grundsätzlich trainiert werden kann.
Folgendes sollte noch beachtet werden:
- Lernrate
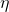 :
:
Die Lernrate ist ein wichtiger Parameter. Wer das Programmier-Beispiel bei sich zum Laufen gebracht hat, einfach mal die Lernrate auf Werte zwischen 10.00 und 0.00000001 setzen, schauen was passiert 🙂 - Globale Minima vs lokale Minima:
Diese lineare zwei-dimensionale Regression ist ziemlich einfach. Neuronale Netze sind hingegen komplexer und haben nicht einfach nur eine simple konvexe Fehlerfunktion. Hier gibt es mehrere Hügel und Täler in der Fehlerfunktion und die Gefahr ist groß, in einem lokalen, nicht aber in einem globalen Minimum zu landen. - Stochastisches Gradientenverfahren:
Wir haben hier das sogenannte Batch-Verfahren verwendet. Dieses ist grundsätzlich besser als die stochastische Methode. Denn beim Batch verwenden wir den gesamten Stapel an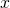 -Werten für die Fehlerbestimmung. Allerdings ist dies bei großen Daten zu rechen- und speicherintensiv. Dann werden kleinere Unter-Stapel (Sub-Batches) zufällig aus den
-Werten für die Fehlerbestimmung. Allerdings ist dies bei großen Daten zu rechen- und speicherintensiv. Dann werden kleinere Unter-Stapel (Sub-Batches) zufällig aus den 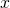 -Werten ausgewählt, der Fehler daraus bestimmt (was nicht ganz so akkurat ist, wie als würden wir den Fehler über alle
-Werten ausgewählt, der Fehler daraus bestimmt (was nicht ganz so akkurat ist, wie als würden wir den Fehler über alle 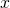 berechnen) und der Gradient bestimmt. Dies ist schon Rechen- und Speicherkapazität, erfordert aber meistens mehr Epochen.
berechnen) und der Gradient bestimmt. Dies ist schon Rechen- und Speicherkapazität, erfordert aber meistens mehr Epochen.
Buchempfehlung
Die folgenden zwei Bücher haben mir bei der Erstellung dieses Beispiels geholfen und kann ich als hilfreiche und deutlich weiterführende Lektüre empfehlen:






 Prof. Dr. Klaus Jung studierte Physik an der TU Berlin, wo er im Bereich der Mathematischen Physik promovierte. Bis 2008 arbeitete er als Leiter F&E bei der Firma LuraTech im Bereich der Dokumentenverarbeitung und Langzeitarchivierung. In der JPEG-Gruppe leitete er die deutsche Delegation bei der Standardisierung von JPEG2000. Seit 2008 ist er Professor für Medieninformatik an der HTW Berlin mit dem Schwerpunkt „Visual Computing“.
Prof. Dr. Klaus Jung studierte Physik an der TU Berlin, wo er im Bereich der Mathematischen Physik promovierte. Bis 2008 arbeitete er als Leiter F&E bei der Firma LuraTech im Bereich der Dokumentenverarbeitung und Langzeitarchivierung. In der JPEG-Gruppe leitete er die deutsche Delegation bei der Standardisierung von JPEG2000. Seit 2008 ist er Professor für Medieninformatik an der HTW Berlin mit dem Schwerpunkt „Visual Computing“.


![Rendered by QuickLaTeX.com \[ x = \begin{bmatrix} x_0\\ x_1\\ x_2\\ x_3\\ \vdots\\ x_n \end{bmatrix} \]](https://data-science-blog.com/de/wp-content/ql-cache/quicklatex.com-3a7aa03dea498a7231e3e497e3e5673d_l3.png)
![Rendered by QuickLaTeX.com \[ w = \begin{bmatrix} w_0\\ w_1\\ w_2\\ w_3\\ \vdots\\ w_n \end{bmatrix} \]](https://data-science-blog.com/de/wp-content/ql-cache/quicklatex.com-c70ad1733451ddc4512b23f2c739f80e_l3.png)
![Rendered by QuickLaTeX.com \[ x = \begin{bmatrix} 5\\ 12\\ 30\\ 2 \end{bmatrix} \]](https://data-science-blog.com/de/wp-content/ql-cache/quicklatex.com-97145f06e658d2f10086bd8c80293749_l3.png)
![Rendered by QuickLaTeX.com \[ w = \begin{bmatrix} 1\\ 2\\ 5\\ 12 \end{bmatrix} \]](https://data-science-blog.com/de/wp-content/ql-cache/quicklatex.com-6cd08615346cc16d7e8c23bac32c19b9_l3.png)
![Rendered by QuickLaTeX.com \[ z = w^T \cdot x = \big[1\text{ }2\text{ }5\text{ }12\big] \cdot \begin{bmatrix} 5\\ 12\\ 30\\ 2 \end{bmatrix} = 1 \cdot 5 + 2 \cdot 12 + 5 \cdot 30 + 12 \cdot 2 = 203 \]](https://data-science-blog.com/de/wp-content/ql-cache/quicklatex.com-70a3e9e9243199e97c549d1d9b0f44c0_l3.png)



 Alice Albrecht ist Research Engineer bei
Alice Albrecht ist Research Engineer bei