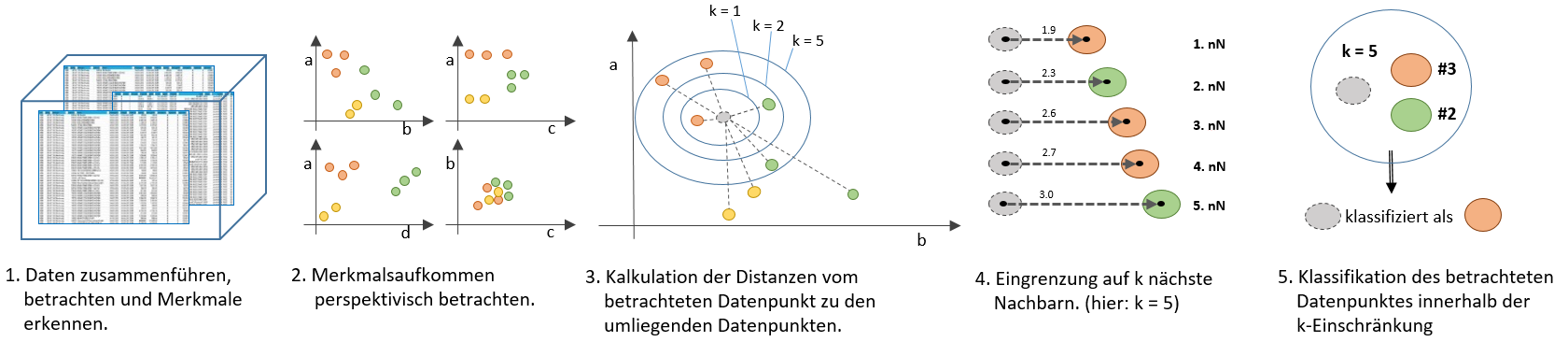
Der Blick für das Wesentliche: Die Merkmalsselektion
In vielen Wissensbasen werden Datensätze durch sehr große Merkmalsräume beschrieben. Während der Generierung einer Wissensbasis wird versucht jedes mögliche Merkmal zu erfassen, um einen Datensatz möglichst genau zu beschreiben. Dabei muss aber nicht jedes Merkmal einen nachhaltigen Wert für das Predictive Modelling darstellen. Ein Klassifikator arbeitet mit reduziertem Merkmalsraum nicht nur schneller, sondern in der Regel auch weitaus effizienter. Oftmals erweist sich ein automatischer Ansatz der Merkmalsselektion besser, als ein manueller, da durchaus Zusammenhänge existieren können, die wir selbst so nicht identifizieren können.
Die Theorie: Merkmalsselektion
Automatische Merkmalsselektionsverfahren unterscheiden 3 verschiedene Arten: Filter, Wrapper und Embedded Methods. Einen guten Überblick über Filter- und Wrapper-Verfahren bieten Kumari et al. in ihrer Arbeit “Filter versus wrapper feature subset selection in large dimensionality micro array: A review” (Download als PDF).
Der Filter-Ansatz bewertet die Merkmale unabhängig des Klassifikators. Dabei werden univariate und multivariate Methoden unterschieden. Univariate Methoden bewerten die Merkmale separat, während der multivariate Ansatz mehrere Merkmale kombiniert. Für jedes Merkmal bzw. jedes Merkmalspaar wird ein statistischer Wert berechnet, der die Eignung der Merkmale für die Klassifikation angibt. Mithilfe eines Schwellwertes werden dann geeignete Merkmale herausgefiltert. Der Filter-Ansatz bietet eine schnelle und, aufgrund der geringen Komplexität, leicht skalierbare Lösung für die Merkmalsselektion. Der Nachteil von Filter-Selektoren besteht in der Missachtung der Abhängigkeiten zwischen den Merkmalen. So werden redundante Merkmale ähnlich bewertet und verzerren später die Erfolgsrate des Klassifikators. Bekannte Beispiele für Filter-Selektoren sind unter anderem die Euklidische Distanz und der Chi-2-Test.
Der Wrapper-Ansatz verbindet die Merkmalsbewertung mit einem Klassifikator. Innerhalb des Merkmalsraumes werden verschiedene Teilmengen von Merkmalen generiert und mithilfe eines trainierten Klassifikators getestet. Um alle möglichen Teilmengen des Merkmalsraumes zu identifizieren, wird der Klassifikator mit einem Suchalgorithmus kombiniert. Da der Merkmalsraum mit Zunahme der Anzahl der Merkmale exponentiell steigt, werden heuristische Suchmethoden für die Suche nach optimalen Teilmengen genutzt. Im Gegensatz zu den Filtern können hier redundante Merkmale abgefangen werden. Die Nutzung eines Klassifikators zur Bewertung der Teilmengen ist zugleich Vor- und Nachteil. Da die generierte Teilmenge auf einen speziellen Klassifikator zugeschnitten wird, ist nicht gewährleistet, dass die Menge auch für andere Klassifikatoren optimal ist. Somit ist dieser Ansatz zumeist abhängig vom gewählten Klassifikator. Zudem benötigt der Wrapper-Ansatz eine viel höhere Rechenzeit. Wrapper-Selektoren werden beispielsweise durch Genetische Algorithmen und Sequentielle Forward/Backward-Selektoren vertreten.
Embedded-Ansätze stellen eine Sonderform der Wrapper-Methode da. Allerdings werden Merkmalssuche und Klassifikatoren-Training nicht getrennt. Die Suche der optimalen Teilmenge ist hier im Modelltraining eingebettet. Dadurch liefern Embedded-Ansätze die gleichen Vorteile wie die Wrapper-Methoden, während die Rechenzeit dabei erheblich gesenkt werden kann. Der reduzierte Merkmalsraum ist aber auch hier vom jeweiligen Klassifikator abhängig. Klassifikatoren, die den Embedded-Ansatz ermöglichen sind beispielsweise der Random-Forest oder die Support-Vector-Maschine.
Entwicklungsgrundlage
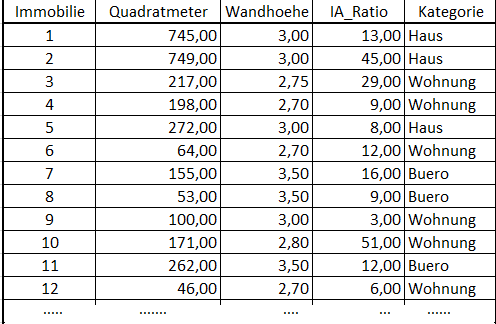
Analog zum letzten Tutorial wird hier Python(x,y) und die Datenbasis „Human Activity Recognition Using Smartphones“ genutzt. Die Datenbasis beruht auf erfassten Sensordaten eines Smartphones während speziellen menschlichen Aktivitäten: Laufen, Treppen hinaufsteigen, Treppen herabsteigen, Sitzen, Stehen und Liegen. Auf den Aufzeichnungen von Gyroskop und Accelerometer wurden mehrere Merkmale erhoben. Die Datenmenge, alle zugehörigen Daten und die Beschreibung der Daten sind frei verfügbar.
(https://archive.ics.uci.edu/ml/datasets/Human+Activity+Recognition+Using+Smartphones)
Alle Daten liegen im Textformat vor. Für ein effizienteres Arbeiten mit der Datenbasis wurden diese im Vorfeld in das csv-Dateiformat überführt.
Python-Bibliotheken
Alle für das Data Mining relevanten Bibliotheken sind in Python(x,y) bereits enthalten. Für die Umsetzung werden folgende Bibliotheken genutzt:
import numpy as np import pandas as pd from sklearn.cross_validation import StratifiedKFold from sklearn.ensemble import RandomForestClassifier from sklearn.feature_selection import f_classif, RFECV, SelectKBest from sklearn.svm import SVC
Die Bibliotheken NumPy und Pandas unterstützen die Arbeit mit verschiedenen Datenstrukturen und scikit-learn umfasst alle Funktionen des maschinellen Lernens.
Daten vorbereiten
Vor der Anwendung der einzelnen Verfahren werden die Daten vorbereitet. Das Data Frame wird eingelesen, die Klassen in numerische Labels überführt und das Datenfeld in Merkmale (X) und Klassenspalte (y) separiert. Weiterhin wird die informationslose Spalte subject entfernt.
index = 0
selected_features = []
# reading database
data = pd.read_csv("data/measures.csv", sep = ';', decimal = ',')
# converting textual class labels to numeric classes like description
data = data.replace({'WALKING': 1, 'WALKING_UPSTAIRS': 2, 'WALKING_DOWNSTAIRS': 3,
'SITTING': 4, 'STANDING': 5, 'LAYING': 6})
# drop subject column
data = data.drop('subject', 1)
# remove class column from data set
print "removing class column from training set.."
X = data.drop('activity', 1)
y = data['activity']
columns = X.columns.values.tolist()
1. Verfahren: RFECV
Der RFECV (Recursive Feature Elimination with Cross Validation) ist ein Vertreter des Wrapper-Ansatzes. In diesem Beispiel wird die Merkmalsselektion mit einem Support Vector Klassifikator kombiniert. Der RFECV berechnet ein Ranking über die einzelnen Merkmale. Dabei bestimmt der Selektor selbst die optimale Menge der Merkmale. Alle Merkmale mit Platz 1 im Ranking bilden den optimalen Merkmalsraum.
''' ########## METHOD 1: RFE with cross validation and SVC ########## '''
print "create classifier for feature selection.."
svc = SVC(kernel = 'linear')
# fit the feature selector
print "create the feature selector.."
rfecv = RFECV(estimator = svc, step = 1, cv = StratifiedKFold(y, 3), scoring = 'accuracy')
print "fit the selector for data set.."
rfecv.fit(X, y)
print "The estimated number of optimal features is: " + str(rfecv.n_features_)
# get the most importent features
feat_importence = zip(rfecv.ranking_, columns)
# prepare list of selected features for new DataFrame
for i in range(len(feat_importence)):
if(feat_importence[i][0] == 1):#>= np.nanmean(rfecv.ranking_)):
selected_features.append(feat_importence[i][1])
print "added feature: " + str(feat_importence[i][1]) + ".."
2. Verfahren: Random Forest-Klassifikator
Der Random-Forest-Klassifikator gehört zu den Modellen, die einen Embedded-Ansatz ermöglichen. Während des Klassifikatoren-Trainings wird jedem Merkmal ein Wert zugeordnet. Je höher der Wert, desto bedeutsamer das Merkmal. Allerdings ist hier eine manuelle Filterung notwendig, da anders als beim RFECV kein internes Optimum ermittelt wird. Mithilfe eines geeigneten Schwellwertes können die zu wählenden Merkmale bestimmt werden. In diesem Beispiel werden alle Merkmale selektiert, die eine Wichtung größer dem Mittelwert erhalten.
''' ########## METHOD 2: Random Forrest Classifier Feat Importance ########## '''
print "create classifier for feature selection.."
rfc = RandomForestClassifier(n_estimators = 500, criterion = 'entropy', max_depth = 4)
rfc = rfc.fit(X, y)
# get the most importent features
feat_importence = zip(rfc.feature_importances_, columns)
# prepare list of selected features for new DataFrame
for i in range(len(feat_importence)):
if(feat_importence[i][0] >= np.mean(rfc.feature_importances_)):
selected_features.append(feat_importence[i][1])
print "added feature: " + str(feat_importence[i][1]) + ".."
3. Verfahren: Select K Best
Das Select K Best-Verfahren gehört den Filter-Ansätzen an. Daher kommt hier anders als bei den anderen beiden Verfahren kein Klassifikator zum Einsatz. Auch in diesem Verfahren wird für jedes Merkmal ein Wert berechnet, der die Wichtigkeit des Merkmals beziffert. Für die Berechnung der Werte können verschiedene Methoden verwendet werden. In diesem Beispiel wird eine Varianzanalyse genutzt (Parameter f_classif). Auch hier wird mithilfe eines manuellen Schwellwertes der reduzierte Merkmalsraum bestimmt.
''' ########## METHOD 3: Select K Best Features ########## '''
print "create classifier for feature selection.."
skb = SelectKBest(f_classif)
skb = skb.fit(X, y)
# get the most importent features
feat_importence = zip(skb.scores_, columns)
# prepare list of selected features for new DataFrame
for i in range(len(feat_importence)):
if(feat_importence[i][0] >= np.nanmean(skb.scores_)):
selected_features.append(feat_importence[i][1])
print "added feature: " + str(feat_importence[i][1]) + ".."
Ergebnisse
Für die Bewertung der einzelnen Selektionsverfahren werden die einzelnen Verfahren in den Data-Mining-Prozess (siehe vorheriges Tutorial: Einstieg in das maschinelle Lernen mit Python(x,y)) integriert. Die nachfolgende Tabelle veranschaulicht die Ergebnisse der Klassifikation der einzelnen Verfahren.
|
Selektionsverfahren |
Anzahl der Merkmale |
Erfolgsrate Klassifikation |
| Ohne |
561 |
93,96% |
| RFECV |
314 |
94,03% |
| Random Forest |
118 |
90,43% |
| Select K Best |
186 |
92,30% |
Durch den RFECV konnte das Ergebnis der Klassifikation leicht verbessert werden. Die anderen Selektionsverfahren, die auch deutlich weniger Merkmale nutzen, verschlechtern das Ergebnis sogar. Dies liegt vor allem an der manuellen Regulierung des Schwellwertes.
Herr Dr. Florian Neukart ist Principal Data Scientist der 
eine Konstante ist.
verdoppeln:
![3D Scatter Plot in Python [Matplotlib]](https://data-science-blog.com/de/wp-content/uploads/sites/5/2016/04/3d-scatter-plot-immobilien-klassifikation-gap.jpg)
Unternehmen, u.a. bei Immobilien.net (heute ImmobilienScout24), PARSHIP und Zanox, tätig und gilt daher als ein etablierter IT-Manager, der seine Kenntnisse als Mentor des Axel Springer Plug and Play Accelerators weitergibt.
automatisierte Kategorisierung von Finanztransaktionen bei uns im Fokus. Damit bieten wir den Nutzern leicht verständliche und genaue Auswertungen ihrer finanziellen Situation sowie eine Übersicht ihrer Einnahmen und Ausgaben. Interessanterweise gibt es unseres Wissens nach noch keine Bank, die Transaktionen direkt für den Kundennutzen kategorisiert.
