Maschinelles Lernen: Parametrisierte und nicht-parametrisierte Verfahren
Das ist Artikel 3 von 4 aus der Artikelserie – Was ist eigentlich Machine Learning?
Maschinelle Lernverfahren können voneinander unterschiedlich abgegrenzt werden, die den meisten Einsteigern bekannte Abgrenzung ist die zwischen überwachten und unüberwachten Verfahren. Eine weitere Abgrenzung zwischen den Lernverfahren, die weit weniger bekannt und verständlich ist, und um die es in diesem Artikel der Reihe gehen soll, ist die Unterscheidung in parametrisierte und nicht parametrisierte Lernverfahren. Gleich vorweg: Parametrisiert und nicht-parametrisierte bezieht sich auf das Modell (Trainingsergebnis), nicht auf die Algorithmen selbst (also nicht Parameter wie k-Werte, Iterations-, Gewichtungs- oder Regularisierungs-Parameter).
Parametrisierte Lernverfahren (parametric learning)
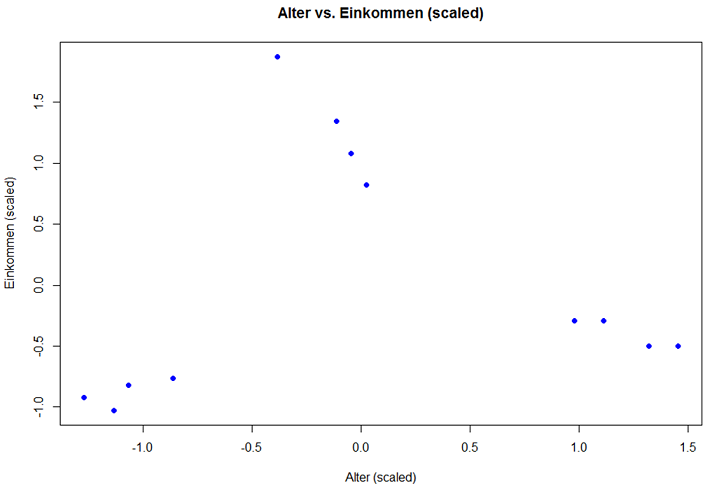
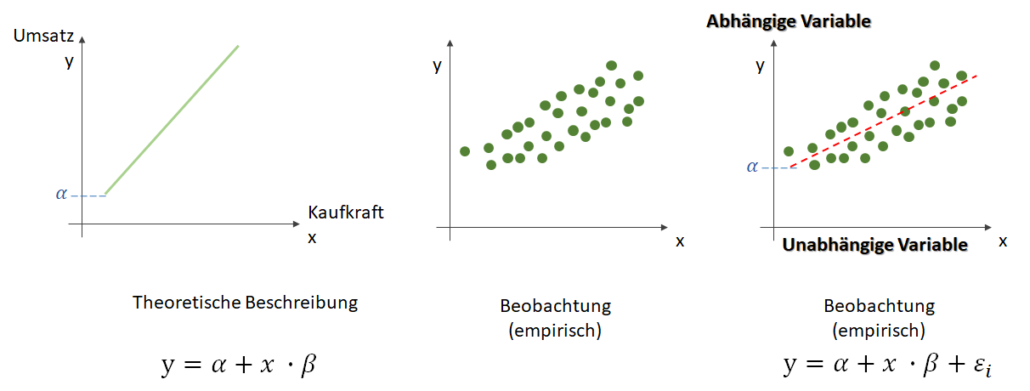
Parametrisierte Lernverfahren sind solche, die über ein Training mit sogenannten Trainingsdaten eine Funktion mit festen Parametern entwickeln, beispielsweise y = f(x) = x³ * a + x² * b + x *c + d. Diese Funktion hat dank einer festgesetzten Anzahl an Parametern eine feste Struktur, und genau dieser Fakt der Parameter-Struktur-Bestimmung a-priori macht das Lernverfahren zu einem parametrischen Lernverfahren. Nach dem Training stehen die Sturkur und die Parameter-Werte fest, beispielsweise y = x³ * 32 + x² * -4 + x * 2 + 102. Diese Funktion beschreibt den Zusammenhang zwischen dem Input x und dem Output y. Am einfachsten kann man sich das Prinzip des parametrischen Lernens demnach mit der Regression vorstellen: Eine Gerade oder eine Kurve wird über ein Trainingslauf durch eine Punktwolke gezogen und daraus die Funktion abgeleitet. Bei der Prädiktion wird diese Funktion dann dazu verwendet, mit den neuen Input-Werten den Output zu berechnen.
Mit dem Festsetzen der Struktur der Funktion bereits vor dem Training sind einige Vor- und Nachteile verbunden:
Parametrische Lernverfahren sind manchmal etwas einfacher zu verstehen, da sich das Modell durchweg als “feste” Formel betrachten lässt. Dieser Vorteil ist jedoch gleichermaßen eine Einschränkung, denn parametrische Verfahren sind eher dazu geeignet, einfachere Zusammenhänge (mit nicht all zu vielen Dimensionen) zu berechnen. Dafür läuft das Training und vor allem die Prädiktion bei parametrischen Verfahren sehr viel schneller ab, als es bei nicht-parametrischen Verfahren der Fall ist, immerhin müssen die Eingabewerte bei der Prädiktion nur in die Funktion mit bekannter Struktur eingefügt und ausgerechnet werden. Man kann sich also merken: Beim parametrischen Lernen stehen die Parameter vorher fest, beim Training werden nur die “richtigen” Werte für die Parameter gefunden.
Schlussendlich kann generell gesagt werden, dass parametrische Funktionen weniger Datenpunkte als nicht-parametrische Lernverfahren benötigen und bei weniger Daten bessere Ergebnisse liefern. Bei sehr großen Datenmengen werden parametrische Funktionen eher schlechter gegenüber nicht-parametrischen Verfahren und neigen etwas zur Unteranpassung.
Zu den parametrischen Lernverfahren gehören:
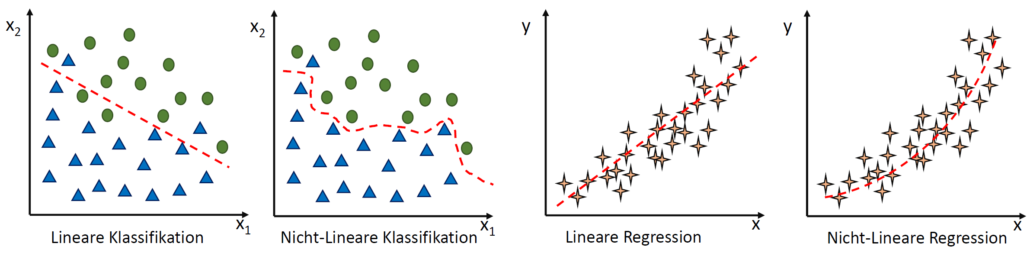
- Lineare und nicht-lineare Regression
- Lineare Diskriminazanalyse
- Logistische Regression
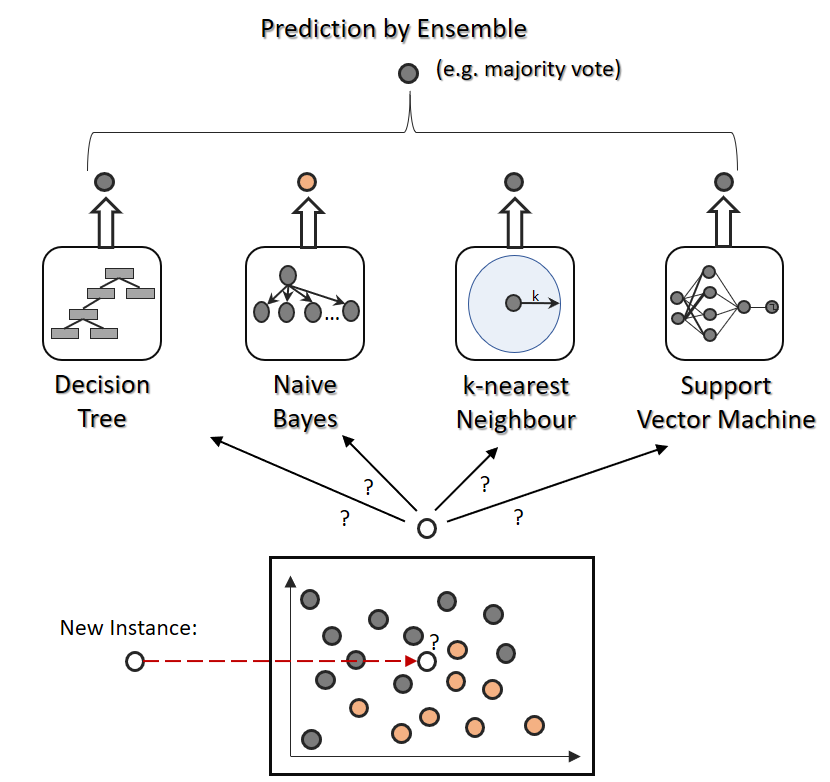
- Naive Bayes Klassifikation
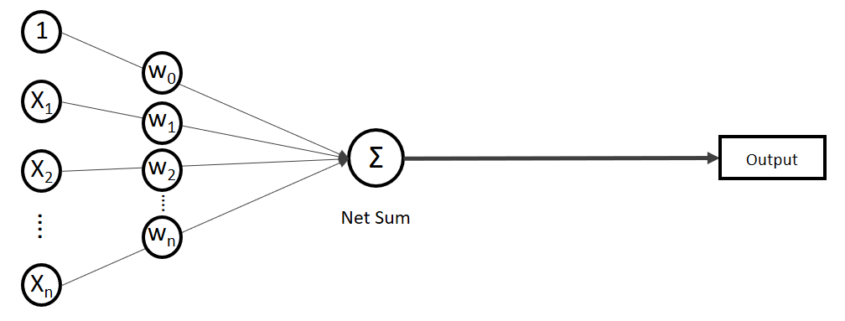
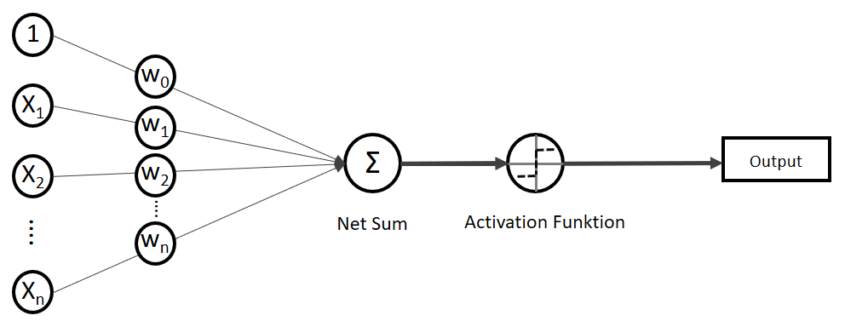
- einfache künstliche neuronale Netze (z. B. MLP)
- lineare Support Vector Machines (SVM)
Nicht-parametrisierte Lernverfahren (nonparametric learning)
Spricht man vom nicht-parametrisierten Lernen, ist die Verwirrung eigentlich vorprogrammiert, denn es bedeutet keinesfalls, dass es keine Parameter gibt, ganz im Gegenteil! Nicht-parametrische Verfahren arbeiten in aller Regel mit sehr viel mehr Parametern als die parametrischen Verfahren. Und nicht-parametrische Verfahren sind häufig dann im Einsatz, wenn die Anzahl an Daten und Dimensionen sehr groß ist und wenn nicht klar ist, welche Dimensionen voneinander unabhängig sind, aber in Abhängigkeit mit dem Klassifikations-/Regressionsergebnis stehen.
Auch nicht-parametrische Lernverfahren entwickeln eine Funktion, die den Zusammenhang zwischen dem Input und dem Output beschreibt. Jedoch wird die Struktur der Funktion vor dem Training nicht konkret über eine bestimmte Anzahl an Parametern festgelegt. Die Anzahl an Parametern wird erst zur Laufzeit des Trainings bestimmt und hier könnte jede neue Zeile in der Tabelle der Trainingsdaten einen neuen Parameter bedeuten (also beispielsweise dazu führen, dass ein neuer Ast eines Entscheidungsbaumes entsteht – oder auch nicht!).
Die Modellstruktur wird nicht über eine Funktion mit festen Parametern festgelegt, sondern bei jeder Prädiktion aus den Daten ermittelt. Tendenziell neigen nicht-parametrisierte Verfahren etwas mehr zur Überanpassung als parametrisierte Verfahren.
Zu den nicht-parametrisierten Lernverfahren gehören:
- k-nächste Nachbarn Klassifikation/Regression
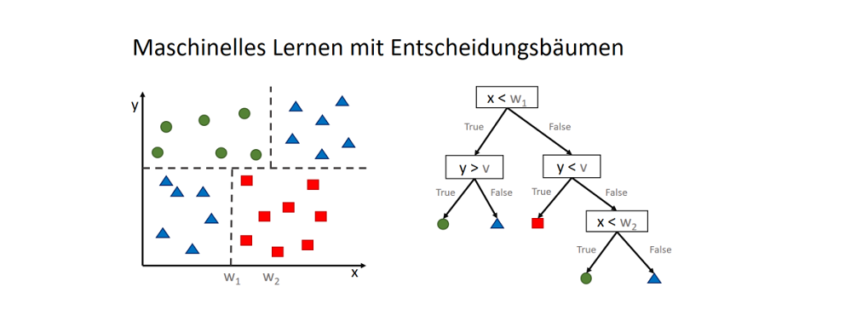
- Entscheidungsbaum Klassifikation/Regression
- Nicht-lineare Support Vector Machines (RBF Kernel SVM)
Kleiner Abgleich des Verständnisses
Der Unterschied zwischen parametrisierten und nicht-parametrisierten Verfahren wird so häufig falsch verstanden, dass es sich lohnt, etwas Zeit in eine kleine Wiederholung zu investieren, jedoch aus der FAQ-Perspektive:
Warum ist die Regressionsanalyse ein parametrisiertes Lernverfahren?
Bei der klassischen Regressionsrechnung müssen wir noch vor dem Training festlegen, über welche Funktion wir trainieren wollen. Eine lineare Funktion wie y = x * a + b? Oder doch lieber eine nicht-lineare Funktion wie y = x² * a + x * b + c? Die Struktur der Funktion, mit der wir die Punktwolke beschreiben möchten und mit der wir dann im Nachgang Prädiktionen auf Basis von neuer x-Werte berechnen möchten, muss vor dem Training bestimmt werden.
Warum ist die k-nächste-Nachbarn-Bestimmung ein nicht-parametrisiertes Lernverfahren?
Hierbei handelt es sich um ein Lernen durch Ähnlichkeitsanalyse. Es werden gelabelte Datenpunkte gesammelt und erst bei der Prädiktion wird die multidimensionale Ähnlichkeit des neuen Datenpunktes mit den bekannten Datenpunkten bestimmt (Matrizen-Bildung über Distanzen zwischen den Datenpunkten im multidimensionalen Vektorraum). Das Modell lässt sich vorher nicht mal adäquat bestimmen.
Das Modell liegt sozusagen in den Daten. Der k-nächste-Nachbarn-Algorithmus (k-nN) zählt deshalb übrigens nicht nur zum nicht-parametrisierten Lernen, sondern ist darüber hinaus auch noch ein instanzbasiertes Lernen (Lazy Learning).
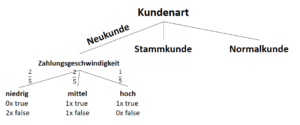
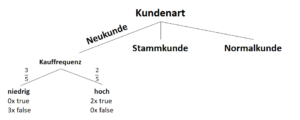
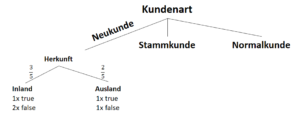
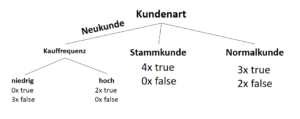
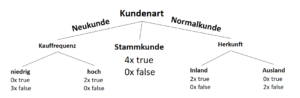
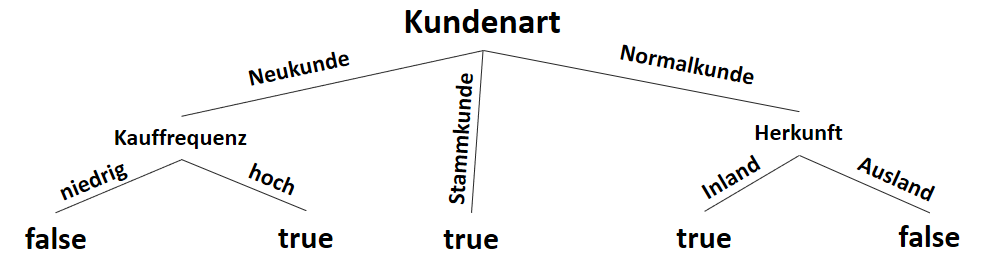
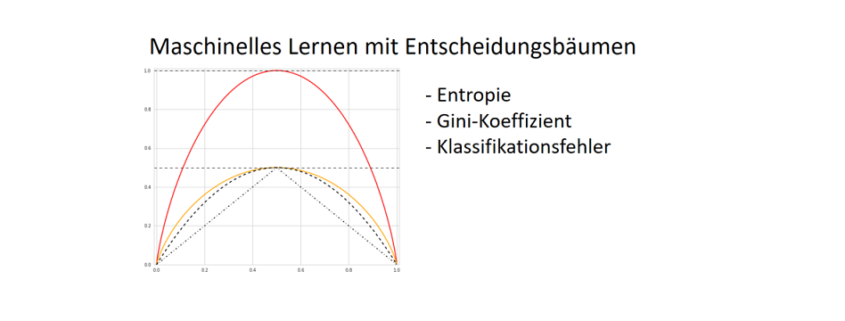
Warum sind Entscheidungsbäume nicht-parametrisierte Lernverfahren?
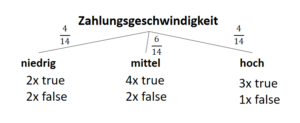
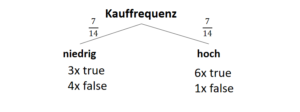
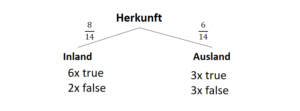
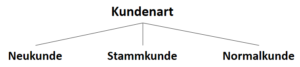
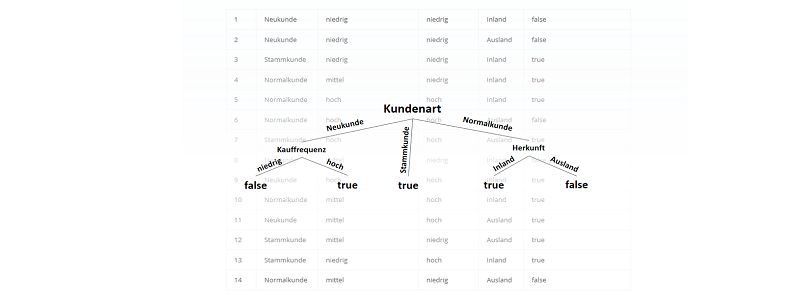
Entscheidungsbäume entwerfen Funktionen, die eine auf das Ergebnis bezogene Datenverteilung beschreiben. Jedoch wird vor der Entstehung dieses Modells (also vor dem Training) nicht die Anzahl der Parameter vorgegeben. Zwar ist es üblich, eine maximale Tiefe des Baumes vorzugeben (auch um Überanpassung zu vermeiden), das Modell (die Struktur des Baumes) hängt jedoch von den Daten ab.
Warum ist Naive Bayes Klassifikation ein parametrisiertes Lernverfahren?
Naive Bayes Klassifikation gilt grundsätzlich als ein parametrisches Lernverfahren. Der Klassifikator errechnet eine Wahrscheinlichkeit, einer bestimmten Klasse zugehörig zu sein, über ein Produkt aus Wahrscheinlichkeiten des Auftretens voneinander (naive) unabhängiger Eingaben (x1, x2,… xn), in der Regel als multinominales Vokabular. Jede Eingabe (eindeutiges Element aus dem Vokabular) ist im Grunde eine Dimension und stellt einen Parameter dar, der im Vorfeld bekannt sein muss.
Es gibt allerdings auch Abwandlungen des Naive Bayes Klassifikators, bei denen mit Dichteschätzungen (1D Kernel Dichteschätzung) gerechnet wird, dann haben wir es wiederum mit Parametern zutun, die erst während der Trainingsphase entstehen.
Warum können Support Vector Machines sowohl parametrisierte als auch nicht-parametrisierte Lernverfahren darstellen?
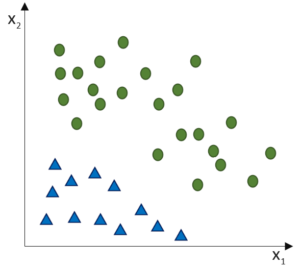
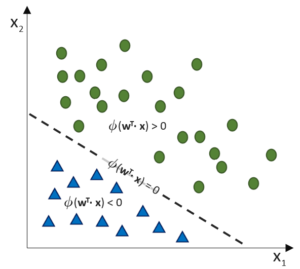
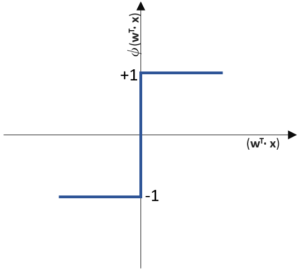
Bei der linearen SVM werden die Werte der Parameter einer linearen Funktion (= feste Anzahl an Parametern) berechnet, die zwei Klassen linear trennt. Bei der nicht-linearen Klassentrennung funktioniert das leider nicht so einfach und es müssen kompliziertere Verfahren verwendet werden. Die bekannteste ist die Radial Basis Function Kernel-basierte SVM. Bei dieser RBF Kernel SVM wird eine Matrix über berechnete Distanzen zwischen den Datenpunkten erstellt und als Parameter verwendet. Da diese Parameter-Anzahl von den Daten abhängt, haben wir es mit einer nicht-parametrisierten Methode zutun (ähnlich wie beim k-nN).


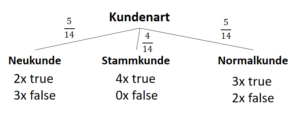
![Rendered by QuickLaTeX.com \[ IG(S, A_{Kundenart}) = - \sum_{i=1}^n \frac{\bigl|S_i\bigl|}{\bigl|S\bigl|} \cdot H(S_i) \]](https://data-science-blog.com/de/wp-content/ql-cache/quicklatex.com-6380891cc61bb855d4208480091fdef0_l3.png)