ID3-Algorithmus: Ein Rechenbeispiel

Dieser Artikel ist Teil 3 von 4 der Artikelserie Maschinelles Lernen mit Entscheidungsbaumverfahren und nun wollen wir einen Entscheidungsbaum aus Daten herleiten, jedoch ohne Programmierung, sondern direkt auf Papier (bzw. HTML :-).

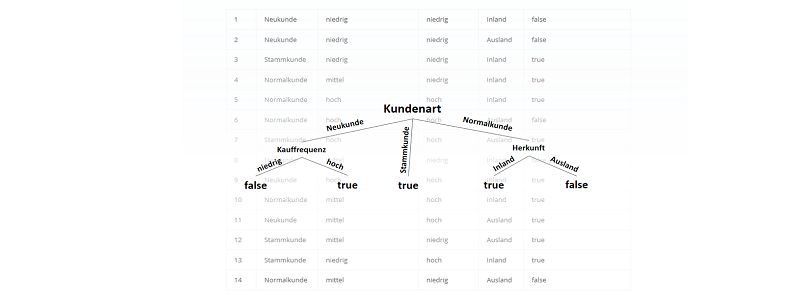
Folgender Datensatz sei gegeben:

Zeile	Kundenart	Zahlungsgeschwindigkeit	Kauffrequenz	Herkunft	Zahlungsmittel: Rechnung?
1	Neukunde	niedrig	niedrig	Inland	false
2	Neukunde	niedrig	niedrig	Ausland	false
3	Stammkunde	niedrig	niedrig	Inland	true
4	Normalkunde	mittel	niedrig	Inland	true
5	Normalkunde	hoch	hoch	Inland	true
6	Normalkunde	hoch	hoch	Ausland	false
7	Stammkunde	hoch	hoch	Ausland	true
8	Neukunde	mittel	niedrig	Inland	false
9	Neukunde	hoch	hoch	Inland	true
10	Normalkunde	mittel	hoch	Inland	true
11	Neukunde	mittel	hoch	Ausland	true
12	Stammkunde	mittel	niedrig	Ausland	true
13	Stammkunde	niedrig	hoch	Inland	true
14	Normalkunde	mittel	niedrig	Ausland	false

Gleich vorweg ein Disclaimer: Der Datensatz ist natürlich überaus klein, ja gerade zu winzig. Dafür würden wir in der Praxis niemals einen Machine Learning Algorithmus einsetzen. Dennoch bleiben wir besser übersichtlich und nachvollziehbar mit diesen 14 Zeilen. Das Lernziel dieser Übung ist es, ein Gefühl für die Erstellung von Entscheidungsbäumen zu erhalten.
Zu beachten ist ferner, dass dieser Datensatz bereits aggregiert ist, denn eigentlich nummerisch abbildbare Daten wurden in Klassen zusammengefasst.

Das Ziel:

Der Datensatz spielt wieder, welchem Kunden (ID) bisher die Zahlung per Rechnung erlaubt und nicht widerrufen wurde. Das Ziel soll sein, eine Vorhersage darüber zu machen zu können, wann ein Kunde per Rechnung zahlen darf und wann nicht (dann per Vorkasse).

Der Algorithmus:

Wir verwenden den ID3-Algorithmus in seiner Reinform. Der ID3-Algorithmus ist der gängigste Algorithmus zum Aufbau datengetriebener Entscheidungsbäume und es gibt mehrere Abwandlungen. Die Vorgehensweise des Algorithmus wird in dem Teil 2 der Artikelserie Entscheidungsbaum-Algorithmus ID3 erläutert.

1. Schritt: Auswählen des Attributes mit dem höchsten Informationsgewinn

Der Informationsgewinn eines Attributes ( $A$ ) im Sinne des ID3-Algorithmus ist die Differenz aus der Entropie ( $E(S)$ ) (siehe Teil 1 der Artikelserie Entropie, ein Maß für die Unreinheit in Daten) des gesamten Datensatzes ( $S$ ) und der Summe aus den gewichteten Entropien des Attributes für jeden einzelnen Wert (Value $i$ ), der im Attribut vorkommt:
$IG(S, A) = H(S) - \sum_{i=1}^n \frac{\bigl|S_i\bigl|}{\bigl|S\bigl|} \cdot H(S_i)$

1.1 Gesamt-Entropie des Datensatzes berechnen

Erstmal schauen wir uns die Entropie des gesamten Datensatzes an. Die Entropie bezieht sich dabei auf das gewünschte Klassifikationsergebnis, also ist die Zahlung via Rechnung erlaubt oder nicht? Diese Frage wird entweder mit true oder false beantwortet.

$H(S) = - \frac{9}{14} \cdot \log_2(\frac{9}{14}) - \frac{5}{14} \cdot \log_2(\frac{5}{14}) = 0.94$

1.2 Berechnung der Informationsgewinne aller Attribute

Berechnen wir nun also die Informationsgewinne über alle Spalten.

Attribut	Subset	Count(true)	Count(false)
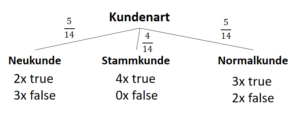
Kundenart	“Neukunde”	2	3
	“Stammkunde”	4	0
	“Normalkunde”	3	2

Wir zerlegen den gesamten Datensatz gedanklich in drei Kategorien der Kundenart und berechnen die Entropie bezogen auf das Klassifikationsziel:

$H(S_{Neukunde}) = - \frac{2}{5} \cdot \log_2(\frac{2}{5}) - \frac{3}{5} \cdot \log_2(\frac{3}{5}) = 0.97$

$H(S_{Stammkunde}) = - \frac{4}{4} \cdot \log_2(\frac{4}{4}) - \frac{0}{4} \cdot \log_2(\frac{0}{4}) = 0.00$

$H(S_{Normalkunde}) = - \frac{3}{5} \cdot \log_2(\frac{3}{5}) - \frac{2}{5} \cdot \log_2(\frac{2}{5}) = 0.97$

Zur Erinnerung, der Informationsgewinn (Information Gain) wird wie folgt berechnet:

$IG(S, A_{Kundenart}) = - \sum_{i=1}^n \frac{\bigl|S_i\bigl|}{\bigl|S\bigl|} \cdot H(S_i)$

Angewendet auf das Attribut “Kundenart”…

$IG(S, A_{Kundenart}) = H(S) - \frac{\bigl|S_{Neukunde}\bigl|}{\bigl|S\bigl|} \cdot H(S_{Neukunde}) - \frac{\bigl|S_{Stammkunde}\bigl|}{\bigl|S\bigl|} \cdot H(S_{Stammkunde}) - \frac{\bigl|S_{Normalkunde}\bigl|}{\bigl|S\bigl|} \cdot H(S_{Normalkunde})$

… erhalten wir der Formal nach folgenden Informationsgewinn:

$IG(S, A_{Kundenart}) = 0.94 - \frac{5}{14} \cdot 0.97 - \frac{4}{14} \cdot 0.00 - \frac{5}{14} \cdot 0.97 = 0.247$

Nun für die weiteren Spalten:

Attribut	Subset	Count(true)	Count(false)
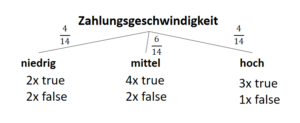
Zahlungsgeschwindigkeit	“niedrig”	2	2
	“mittel”	4	2
	“schnell”	3	1

Entropien für die “Zahlungsgeschwindigkeit”:

$H(S_{niedrig}) = - \frac{2}{4} \cdot \log_2(\frac{2}{4}) - \frac{2}{4} \cdot \log_2(\frac{2}{4}) = 1.00$

$H(S_{mittel}) = - \frac{4}{6} \cdot \log_2(\frac{4}{6}) - \frac{2}{6} \cdot \log_2(\frac{2}{6}) = 0.92$

$H(S_{schnell}) = - \frac{3}{4} \cdot \log_2(\frac{3}{4}) - \frac{1}{4} \cdot \log_2(\frac{1}{4}) = 0.81$

So berechnen wir wieder den Informationsgewinn:

$IG(S, A_{Zahlungsgeschwindigkeit}) = H(S) - \frac{\bigl|S_{niedrig}\bigl|}{\bigl|S\bigl|} \cdot H(S_{niedrig}) - \frac{\bigl|S_{mittel}\bigl|}{\bigl|S\bigl|} \cdot H(S_{mittel}) - \frac{\bigl|S_{schnell}\bigl|}{\bigl|S\bigl|} \cdot H(S_{schnell})$

Einsatzen und ausrechnen:

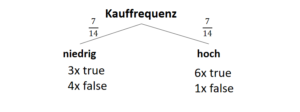
$IG(S, A_{Zahlungsgeschwindigkeit}) = 0.94 - \frac{4}{14} \cdot 1.00 - \frac{6}{14} \cdot 0.92 - \frac{4}{14} \cdot 0.81 = 0.029$

Und nun für die Spalte “Kauffrequenz”:

Attribut	Subset	Count(true)	Count(false)
Kauffrequenz	“niedrig”	3	4
Kauffrequenz	“hoch”	6	1

Entropien:

$H(S_{niedrig}) = - \frac{3}{7} \cdot \log_2(\frac{3}{7}) - \frac{4}{7} \cdot \log_2(\frac{4}{7}) = 0.99$

$H(S_{hoch}) = - \frac{6}{7} \cdot \log_2(\frac{6}{7}) - \frac{1}{7} \cdot \log_2(\frac{1}{7}) = 0.59$

Informationsgewinn:

$IG(S, A_{Kauffrequenz}) = H(S) - \frac{\bigl|S_{niedrig}\bigl|}{\bigl|S\bigl|} \cdot H(S_{niedrig}) - \frac{\bigl|S_{hoch}\bigl|}{\bigl|S\bigl|} \cdot H(S_{hoch})$

Einsetzen und Ausrechnen:

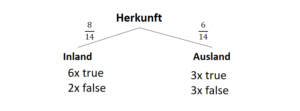
$IG(S, A_{Kauffrequenz}) = 0.94 - \frac{7}{14} \cdot 1.00 - \frac{7}{14} \cdot 0.59 = 0.150$

Und last but not least die Spalte “Herkunft”:

Attribut	Subset	Count(true)	Count(false)
Herkunft	“Inland”	6	2
Herkunft	“Ausland”	3	3

Entropien:

$H(S_{Inland}) = - \frac{6}{8} \cdot \log_2(\frac{6}{8}) - \frac{2}{8} \cdot \log_2(\frac{2}{8}) = 0.81$

$H(S_{Ausland}) = - \frac{3}{6} \cdot \log_2(\frac{3}{6}) - \frac{3}{6} \cdot \log_2(\frac{3}{6}) = 1.00$

Informationsgewinn:

$IG(S, A_{Herkunft}) = H(S) - \frac{\bigl|S_{Inland}\bigl|}{\bigl|S\bigl|} \cdot H(S_{Inland}) - \frac{\bigl|S_{Ausland}\bigl|}{\bigl|S\bigl|} \cdot H(S_{Ausland})$

Einsetzen und Ausrechnen:

$IG(S, A_{Herkunft}) = 0.94 - \frac{8}{14} \cdot 0.81 - \frac{6}{14} \cdot 1.00 = 0.05$

2. Schritt: Anlegen des Wurzel-Knotens

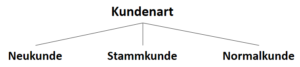
Der Informationsgewinn ist für das Attribut “Kundenart” am größten, daher entscheiden wir uns im Sinne des ID3-Algorithmus für dieses Attribut als Wurzel-Knoten.

3. Schritt: Rekursive Wiederholung (!!!)

Nun stellt sich natürlich die Frage: Wie geht es weiter?

Der Algorithmus kann eigentlich nur eines: Einen Wurzelknoten finden. Diesen Vorgang müssen wir nun nur noch rekursiv wiederholen, und das tun wir wie folgt.

Der Datensatz wurde bereits aufgeteilt in die drei Kundenarten. Für jede Kundenart ergibt sich jeweils ein Subset mit den verbleibenden Attributen. Für alle drei Subsets erstellen wir dann wieder einen Wurzelknoten, so dass ein neuer Ast entsteht.

3.1 Erster Rekursionsschritt

Machen wir also weiter und bestimmen wir das nächste Attribut nach der Kundenart, für die Fälle Kundenart = “Neukunde”:

Zeile	Kundenart	Zahlungsgeschwindigkeit	Kauffrequenz	Herkunft	Zahlungsmittel: Rechnung?
1	Neukunde	niedrig	niedrig	Inland	false
2	Neukunde	niedrig	niedrig	Ausland	false
8	Neukunde	mittel	niedrig	Inland	false
9	Neukunde	hoch	hoch	Inland	true
11	Neukunde	mittel	hoch	Ausland	true

Die Entropie des Gesamtdatensatzes (ja, es ist für diesen Schritt betrachtet der gesamte Datensatz!) ist wie folgt:

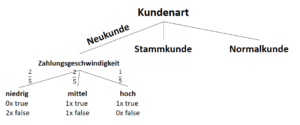
$H(S_{Neukunde}) = - \frac{2}{5} \cdot \log_2(\frac{2}{5}) - \frac{3}{5} \cdot \log_2(\frac{3}{5}) = 0.97$

Die Entropie ist weit weg von einer bestimmten Wahrscheinlichkeit (nahe der Gleichverteilung). Daher müssen wir hier nochmal ansetzen und losrechnen:

Entropien für “Zahlungsgeschwindigkeit” bei Neukunden:

$H(S_{niedrig}) = 0.00$

$H(S_{mittel}) = 1.00$

$H(S_{hoch}) = 0.00$

Informationsgewinn des Attributes “Zahlungsgeschwindigkeit” bei Neukunden:

$IG(S_{Neukunde},A_{Zahlungsgeschwindigkeit}) = 0.97 - \frac{3}{5} \cdot 0.00 - \frac{2}{5} \cdot 1.00 - \frac{1}{5} \cdot 0.00 = 0.57$

Betrachtung der Spalte “Kauffrequenz” bei Neukunden:

Entropien für “Kauffrequenz” bei Neukunden:

$H(S_{niedrig}) = 0.00$

$H(S_{hoch}) = 0.00$

Informationsgewinn des Attributes “Kauffrequenz” bei Neukunden:

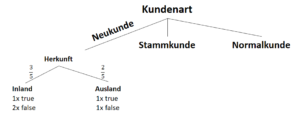
$IG(S_{Neukunde},A_{Kauffrequenz}) = 0.97 - \frac{3}{5} \cdot 0.00 - \frac{2}{5} \cdot 0.00 = 0.97$

Betrachtung der Spalte “Herkunft” bei Neukunden:

Entropien für “Herkunft” bei Neukunden:

$H(S_{Inland}) = 0.92$

$H(S_{hoch}) = 1.00$

Informationsgewinn des Attributes “Herkunft” bei Neukunden:

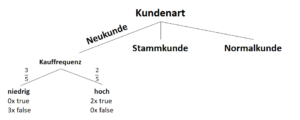
$IG(S_{Neukunde},A_{Herkunft}) = 0.97 - \frac{3}{5} \cdot 0.92 - \frac{2}{5} \cdot 1.00 = 0.018$

Wir entscheiden uns also für das Attribut “Kauffrequenz” als Ast nach der Entscheidung “Neukunde”, denn dieses Attribut bring uns den größten Informationsgewinn und trennt uns die Unterscheidung für oder gegen das Zahlungsmittel “Rechnung” eindeutig auf.

3.1 Zweiter Rekursionsschritt

Was passiert mit der Kundenart “Stammkunde”?

Zeile	Kundenart	Zahlungsgeschwindigkeit	Kauffrequenz	Herkunft	Zahlungsmittel: Rechnung?
3	Stammkunde	niedrig	niedrig	Inland	true
7	Stammkunde	hoch	hoch	Ausland	true
12	Stammkunde	mittel	niedrig	Ausland	true
13	Stammkunde	niedrig	hoch	Inland	true

Die Antwort ist einfach: Nichts!
Wer ein Stammkunde ist, dem wurde stets die Zahlung per Rechnung erlaubt.

$H(S_{Stammkunde}) = 0.0$

3.1 Dritter Rekursionsschritt

Fehlt nun nur noch die Frage nach der Unterscheidung von Normalkunden.

Zeile	Kundenart	Zahlungsgeschwindigkeit	Kauffrequenz	Herkunft	Zahlungsmittel: Rechnung?
4	Normalkunde	mittel	niedrig	Inland	true
5	Normalkunde	hoch	hoch	Inland	true
6	Normalkunde	hoch	hoch	Ausland	false
14	Normalkunde	mittel	niedrig	Ausland	false

Zwar ist die Entropie des Subsets der Normalkunden…

$H(S_{Normalkunde}) = 1.0$

… denkbar schlecht, da maximal. Aber wir können genauso vorgehen, wie wir es bei dem Subset der Neukunden getan haben. Ich nehme es nun aber vorweg: Wenn wir uns den Datensatz näher ansehen, erkennen wir, dass wir diese Gesamtentropie von 1.0 für das Subset “Normalkunde” nicht mit den Attributen “Kauffrequenz” oder “Zahlungsgeschwindigkeit” reduzieren können, da dieses auch für sich betrachtet in Entropien der Größe 1.0 erhalten werden. Das Attribut “Herkunft” hingegen teilt den Datensatz sauber in true und false auf:

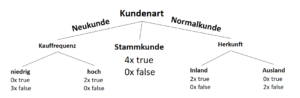Somit ist der Informationsgewinn für das Attribut “Herkunft” am größten und wir haben unseren Baum komplett und – glücklicherweise – eindeutig bestimmen können!

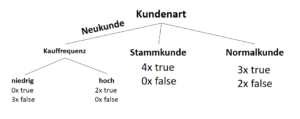
Ergebnis: Der Entscheidungsbaum

Somit haben wir den Entscheidungsbaum über den ID3-Algorithmus erstellt, der eine Auskunft darüber macht, ob einem Kunden die Zahlung über Rechnung (statt Vorkasse) erlaubt wird:

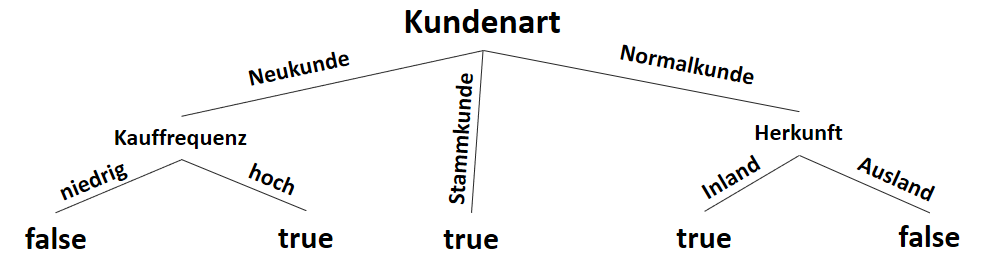true = Rechnung als Zahlungsmittel erlaubt
false = Rechnung als Zahlungsmittel nicht erlaubt

About Author

Benjamin Aunkofer

Benjamin Aunkofer ist Gründer von DATANOMIQ und Hochschul-Dozent für Data Science und Data Strategy. Darüber hinaus arbeitet er als Interim Head of Business Intelligence und gibt Seminare/Workshops zu den Themen BI, Data Science und Machine Learning für Unternehmen.

See author's posts

ID3-Algorithmus: Ein Rechenbeispiel