Interview mit Prof. Dr. Kai Uwe Barthel über Data Science mit Deep Learning
Interview mit Prof. Dr. Barthel, Chief Visionary Officer der Pixolution GmbH in Berlin, über Funktion, Einsatz und Einstieg in künstliche neuronale Netze.
Prof. Kai Barthel ist Gründer und CVO der Pixolution GmbH, ein Unternehmen, das Deep Learning dazu einsetzt, Bilder über ihre Pixelinhalte automatisiert verstehen zu können. Darüber hinaus ist Prof. Barthel in der Forschung und Lehre für Medieninformatik und Visual Computing an der Hochschule für Technik und Wirtschaft in Berlin tätig.
Data Science Blog: Welcher Weg hat Sie zu einem führenden Experten für Deep Learning und zur Gründung der Pixolution GmbH geführt?
Im Prinzip bin ich über mein Interesse an elektronischen Musikinstrumenten auf den Weg zur Analyse von Bits und Bytes gekommen. Als Schüler war ich von den neuen Möglichkeiten der Klangerzeugung fasziniert. 1980, zwei Jahre vor meinem Abitur, baute ich einen eigenen Synthesizer, ohne wirklich zu verstehen, was ich dort eigentlich tat.
Daraufhin studierte ich Elektrotechnik mit Fokus auf Signalverarbeitung, blieb nach dem Diplom diesem Themenbereich treu und arbeitete als wissenschaftlicher Mitarbeiter an der TU Berlin, wo ich zum Thema Bildkompression promovierte.
In diesem Kontext bin ich auf MPEG-7 gestoßen und fand das Konzept sehr spannend. MPEG-7 war im Gegensatz zu MPEG-1, 2 und 4 kein Kompressionsstandard für Video- oder Audiodaten, sondern die Idee bestand darin, Metadaten von Mediendateien zu erzeugen. Ich befasste mich mit der automatisierten Beschreibung von Bildern, ohne manuelle Verschlagwortung, allein auf Basis der Pixelwerte. Spätestens das war für mich der erste Schritt in Richtung maschinelles Lernen.
Unser erster Erfolg war das Programm ImageSorter, das wir im Jahr 2006 als Freeware veröffentlichten. Hiermit konnte man hunderte von Bildern visuell sortiert darstellen und somit gesuchte Bilder schneller finden. Wir bekamen rasch unerwartete Anfragen aus der Industrie, wie etwa von CEWE mit der Aufgabe, Bilder für Fotobücher automatisch zu sortieren. Aus diesem Bedarf heraus haben wir dann die Pixolution GmbH gegründet. Auch Mauritius Images, eine der ältesten Bildagenturen Deutschlands, hatte unseren Algorithmus eingesetzt, mit dem die Ergebnisse einer Bildsuche inhaltsbasiert sortiert präsentiert wurden und somit die Nutzer in die Lage versetzten, mehrere hundert Bilder gleichzeitig zu erfassen.
Data Science Blog: Im Gegensatz zu anderen Anbietern künstlicher Intelligenz, befassen Sie sich nicht nur mit der einfachen Klassifikation von Bildern, sondern Sie verwenden Deep Learning, um dem Computer ein generelles Verständnis von Bildern zu verleihen.
Deep Learning ist ein Mittel zum Zweck, womit sich viele Aufgaben lösen lassen. Heute analysieren wir Bilder automatisiert über künstliche neuronale Netze, da diese in den letzten Jahren enorm an Reife hinzugewonnen haben. Hiermit lassen sich neben der Klassifikation „was ist der Inhalt eines Bildes?“ eine Reihe weiterer Aufgaben lösen. Hierzu gehört neben der automatischen Verschlagwortung unbekannter Bilder, das Finden ähnlicher Bilder, die Detektion von Duplikaten im Datenbestand, aber auch die Beantwortung sehr spezifischer Fragestellungen, wie etwa nach der Qualität, der Stimmung oder dem Stil eines Bildes. Einige Beispiele sind auf unserer Webseite http://www.visual-computing.com zu finden. Natürlich lässt sich Deep-Learning auch auf andere Datentypen anwenden. Das kennen wir alle von Sprachassistenten wie Siri oder Email-Spamfiltern etc.
Unser Hauptprodukt bei Pixolution ist ein Plugin für Solr, womit wir ein klassisches Dokumentensuchsystem in die Lage versetzen, auch Bilder (z.B. von Agentur- oder Produktdatenbanken) gleichzeitig nach konventionellen Metadaten und visuellen/inhaltlichen Kriterien durchsuchbar zu machen. Dafür müssen die Bilder von der Maschine „verstanden“ werden.
Data Science Blog: Was bedeutet Deep Learning denn eigentlich im Kontrast zu Machine Learning? Wo beginnt Deep Learning und – als obligatorische Frage – ist Deep Learning ein überzogenes Buzzword?
Machine Learning ist im Prinzip der Oberbegriff aller Verfahren, bei denen Computer zu einer bestimmten Fragestellung selber den Algorithmus zur Lösung generieren können. Heute wird der Begriff „Machine Learning“ sicherlich etwas verschwenderisch verwendet. Zum Teil werden oft schon einfachere Verfahren wie beispielsweise Decision Trees oder K-means-Clustering als Machine Learning „verkauft“. Das eigentliche Machine Learning verwendet unterschiedliche Arten künstlicher neuronaler Netze. Einfache Aufgaben lassen sich mit kleinen neuronalen Netzen mit zwei bis vier Schichten lösen, dies reicht beispielsweise für die Erkennung von handschriftlichen Ziffern.
Deep Learning verwendet neuronale Netze mit deutlich mehr Schichten (bis hin zu Hunderten). Erst mit diesen vielen Schichten, die insgesamt Tausende bis Millionen von Netzwerkgewichten (zu lernende Parameter) haben, werden Lösungen für wirklich komplexe Aufgaben möglich.
Deep Learning ist ein Unterbereich von Machine Learning. Für mich ist Deep Learning kein Buzzword, denn die Lösungsmöglichkeiten von komplexen Aufgaben sind tiefgreifend. Es hat sich in den letzten Jahren einiges getan, so dass wirklich hochkomplizierte Aufgaben lösbar geworden sind.
Data Science Blog: Deep Learning gilt allerdings auch als Blackbox. Für den Menschen nachvollziehbare Entscheidungen von der Maschine sind somit nicht mehr möglich. Wie nachteilig wirkt sich das auf den Einsatz aus?
Die einzelnen Bestandteile eines künstlichen neuronalen Netzes sind recht simpel. Aus diesen elementaren Teilen werden neue Lösungsmodelle zusammengesetzt. Die Summe dieser Bestandteile und deren Interaktion wird jedoch schnell sehr hoch, so dass die Netze tatsächlich nicht mehr detailliert nachvollziehbar sind. Es stimmt also, dass künstliche neuronale Netze ab einer gewissen Größe zur Blackbox werden. Und es gibt auch Beispiele, mit denen solche Netze in die Irre geführt werden können. Nichtsdestotrotz liefern diese Netze die besten Ergebnisse, so dass dieser Nachteil in Kauf genommen wird – denn was wären die Alternativen? Gerade im Bereich der Analyse und der Visualisierung der Funktionsweise von neuronalen Netzen gibt es viele Forschungsansätze, die das Verständnis mittelfristig deutlich verbessern werden. In vielen Bereichen sind die Klassifikationsergebnisse, die mit ausreichend vielen Beispielen trainiert wurden, besser als menschliche Experten. Hinzu kommt, dass menschliche Experten oft auch nicht genau begründen können, warum Sie zu einer bestimmten Eischätzung kommen, letztlich gleichen sie eine konkrete Fragestellung mit ihren umfangreichen Erfahrungen ab, was eine recht ähnliche Herangehensweise ist.
Data Science Blog: Welche Anwendungsszenarien für künstliche neuronale Netze gibt es?
Eine häufig verwendete Definition dessen, was Deep Learning an Aufgaben bewältigen kann, lautet: Es sind die Aufgaben, die ein Mensch in einer Sekunde lösen kann, ohne darüber nachdenken zu müssen. Wir können ein Netz darauf trainieren und es auf eine Aufgabe sozusagen „abrichten“. Im Unternehmen können künstliche neuronale Netze z. B. auffällige Verhaltensweisen von Maschinen identifizieren. Für mich geht es im Wesentlichen darum, der Maschine beizubringen, Bilder zu verstehen.
Das Verständnis von akustischen Signalen und Bildern ist schon lange ein Ziel der Informatik, es wird jedoch erst seit kurzem in zufriedenstellendem Ausmaß erreicht. Mit künstlichen neuronalen Netzen können Bilder vom Computer analysiert und Aussagen über ihre Inhalte gemacht werden. In den ersten Terminator-Filmen mit Arnold Schwarzenegger war es noch Science Fiction, dass die Welt aus Kamerabildern heraus analysiert und verstanden wurde. Inzwischen ist dies möglich. Was sicherlich noch eine Weile dauern wird, sind die Lösungen von Aufgaben, die eine zeitliche Planung oder ein strategisches Vorgehen benötigen.
Data Science Blog: Für welche Anwendungen in der Industrie ist Deep Learning schon gegenwärtig nutzbar?
Als Beispiel sei hier die industrielle Bildverarbeitung genannt. Bis vor kurzem war dies eine Sequenz von fein abgestimmten Schritten, wobei mit genau vordefinierten Bedingungen, wie etwa dem Bildhintergrund und einer bestimmten Beleuchtung, gearbeitet wurde. Dann wurde von einem Bildverarbeitungsexperten eine Kaskade von speziellen Bildverarbeitungsalgorithmen aufgesetzt, die das spezifische Problem lösten. Dies Prinzip hat meist sehr gut funktioniert, aber diese Ansätze ließen sich nicht gut generalisieren und mussten für jedes neue Problem wieder neu angepasst werden.
Beim Deep Learning ist die Situation eine ganz andere. Hier geht es darum, genügend Beispiele an Bildern und den dazugehörigen Ergebnissen zu haben. Das System lernt dann alleine, wie aus den Bildern bzw. Pixeln mit welchen Operationen die gewünschten Ergebnisse vorhergesagt werden können.
Für jeden, dem das noch zu abstrakt ist: Auch sehr spezifische Aufgaben aus der Industrie können mit neuronalen Netzen bewältigt werden. In der Fertigung und Montage können z.B. Nachfüllbehälter für Schrauben mit Kameras ausgestattet werden. Die Algorithmen erkennen dann über die Kamerabilder nicht nur zuverlässig, ob sich noch genügend viele Schrauben im Behälter befinden, sondern z. B. auch, um welche Schrauben es sich genau handelt.
Letztendlich spielt Deep Learning gerade in vielen Industrieanwendungen eine Rolle, so auch in der Spracherkennung oder dem Konzept des autonomen Fahrens. Das Hauptproblem beim Deep Learning ist nicht so sehr die Frage nach dem optimalen Netzwerk, sondern es besteht eher darin, genügend gute Beispiele zu haben, anhand derer die Netzwerke dann trainiert werden können.
Data Science Blog: Welche Entwicklungen der vergangenen Jahre ermöglichten die enormen Erfolge in Sachen Deep Learning?
Deep Learning wird in der Regel nicht mit CPUs, der zentralen Recheneinheit eines Computers, durchgeführt, sondern über GPUs, also speziell für Grafikberechnung ausgelegte Prozessoren – übrigens auch dann, wenn keine Bilder sondern andere Daten analysiert werden sollen. GPUs sind spezialisiert auf die Berechnung von Fließkommazahlen und können Matrizenmultiplikationen parallelisieren und somit etliche Male schneller als die CPU durchführen. Die heutige Hardware ermöglicht die notwendige Rechenleistung für künstliche neuronale Netze bereitzustellen.
Zum anderen benötigen Deep Learning Algorithmen sehr große Mengen an Trainingsdaten. Um ein neuronales Netz auf Bilder zu trainieren, um beispielsweise Katzen von Hunden zu unterscheiden, braucht es tausende Bilder mit Katzen und Hunden aus unterschiedlichen Perspektiven, Farben und Formen. Wir profitieren davon, dass sich diverse Menschen die Mühe gemacht haben, Millionen von Beispielbildern exakt zu beschriften und der Wissenschaft für das Training zur Verfügung zu stellen.
Data Science Blog: Was hat sich denn seitens der Algorithmen getan? Es heißt, dass die Backpropagation als Lernmethodik der große Clou bei neuronalen Netzen sei?
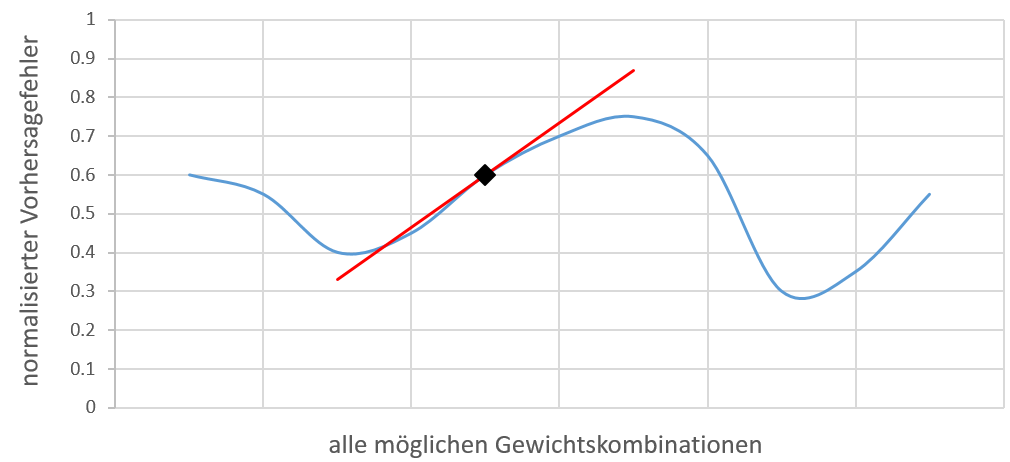
Backpropagation ist ein Lernverfahren für neuronale Netze, mit dem sich Aufgaben lösen lassen, bei denen die, zu den Eingangsdaten gehörigen/gewünschten Ergebnisse bekannt sind (supervised learning). Nach jedem Durchlauf der Daten durch das Netzwerk (Forward-Pass) gibt es einen Fehler im Endergebnis. Das Backpropagation-Verfahren arbeitet auf Basis der Gradientenabstiegsmethode und passt sukzessive die Netzwerkgewichte so an, dass der Fehler kleiner wird.
Eigentlich ist das Backpropagation-Verfahren ist schon recht lange bekannt. Neben der Beschleunigung der Computer und der Verfügbarkeit geeigneter Trainingsdaten, gab es jedoch erst in den letzten Jahren die notwendigen algorithmischen Fortschritte, mit denen es möglich wurde, auch extrem großen Netzwerke erfolgreich zu trainieren. Hier sind die Convolutional Netzwerke zu nennen, die insbesondere das Verstehen von Bildern (aber auch andere hochkomplexe Problemstellungen) erst möglich machten. Convolutional Netzwerke verwenden nicht für jeden Pixel ein individuelles Gewicht. Vielmehr wird ein Satz von zu erlernenden Filtern mit verhältnismäßig wenig Parametern/Gewichten verwendet. Jede Filterung erzeugt ein neues Bild, Pooling-Verfahren reduzieren die Auflösung dieser neu erzeugten Bilder, indem nur besonders aktive Neuronen beibehalten werden. Durch diese beiden Maßnahmen lässt sich die Zahl der Netzwerkgewichte gegenüber vollvernetzten Netzwerken deutlich reduzieren und ein erfolgreiches Netzwerktraining auch mit begrenzten Mengen an Beispieldaten erzielen.
Data Science Blog: Wie kann man sich denn vorstellen, wie so ein künstliches neuronales Netz funktioniert?
Die Grundidee ist an die biologischen Arbeitsweise im Gehirn angelehnt. Schichten von Neuronen erkennen bestimmte Muster. Auf den ersten Schichten sind dies zunächst einfache Strukturen wie Ecken, Kanten oder Farbübergänge. Die Neuronen führen also eine Funktion/Filterung aus, die jeden Eingabewert mit einer bestimmten Gewichtung multipliziert und diese Teilergebnisse aufsummiert. Eine nicht-lineare Funktion erzeugt hieraus einen Aktivierungswert, den Output, der angibt, ob ein entsprechendes Muster vorliegt. Dieser Output ist dann wiederum der Input für die nächste Netzwerkschicht ist. In den nächsten Schichten werden die einfachen Strukturen dann zu komplizierteren Mustern zusammengesetzt. Viele Linien aus unterschiedlichen Teilmustern ergeben beispielsweise Gitter, zwei senkrechte Linien ein Kreuz, usw. Letztlich lernen die Netzwerke aus allen möglichen Konstellationen der Eingangsdaten diejenigen Kombinationen, die in realen Daten/Bildern auftreten. Auf den letzten Schichten werden dann komplexere Muster erkannt, etwa mehrere Kreise und Konturlinien, die in einer bestimmten Anordnung beispielsweise ein menschliches Gesicht darstellen. Soll das künstliche neuronale Netz dieses Muster erkennen können, rechnen wir über die Backpropagation die Gewichtungen aus, die anhand der Beispielbilder – manche zeigen ein menschliches Gesicht, andere nicht – den kleinstmöglichen Klassifizierungsfehler erzeugen. Es wird beim Trainieren eines neuronalen Netzes also eine Funktion ermittelt, die den Input (die Bilddaten) auf den entsprechend Output (die korrekte Kategorie des Bildes) abbildet.
Data Science Blog: Was würden Sie Data Scientists raten, die in Deep Learning einsteigen möchten? Wie bewältigt man den Einstieg?
Ich würde nicht direkt ins Deep Learning einsteigen, sondern sicher erstmal versuchen, mich mit allgemeinen Methoden des maschinellen Lernens vertraut zu machen. Hierzu gehören Techniken wie das Clustering oder lineare/logistische Regression. Ich denke, dass jeder, der in diesen Bereich einsteigen will, wirklich einmal selber ein einfachstes Netzwerk (z.B. XOR und darüber hinaus) per Hand programmiert haben sollte. Hierfür können Tools wie MATLAB oder Octave verwendet werden. Erst im Anschluss, wenn man grundlegenden Kenntnisse erlangt hat, können Frameworks wie z.B. TensorFlow verwendet werden, was den Vorteil hat, dass einem die Bestimmung der mathematischen Ableitungen der Netzwerkstrukturen abgenommen wird. Dann lassen sich auch bestehende Lösungen besser nachvollziehen bzw. anpassen, um das Rad für den produktiven Lauf nicht noch einmal neuerfinden zu müssen, sondern die gewünschten Implementierungen ohne Umwege direkt angehen zu können.
Herr Dr. Florian Neukart ist Principal Data Scientist der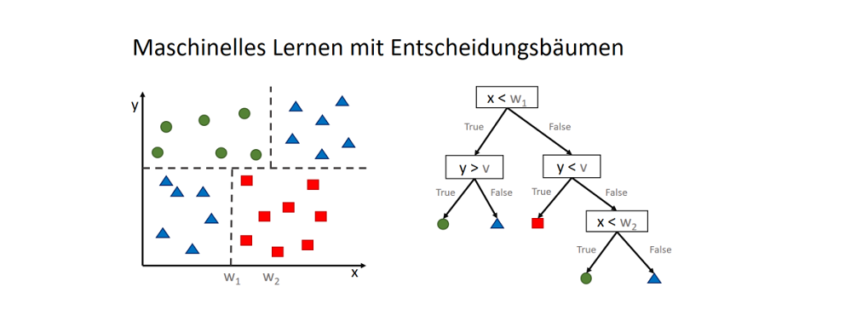 
![3D Scatter Plot in Python [Matplotlib]](https://data-science-blog.com/de/wp-content/uploads/sites/5/2016/04/3d-scatter-plot-immobilien-klassifikation-gap.jpg)
