Entropie – Und andere Maße für Unreinheit in Daten

Dieser Artikel ist Teil 1 von 4 der Artikelserie Maschinelles Lernen mit Entscheidungsbaumverfahren.

Hierarchische Klassifikationsmodelle, zu denen das Entscheidungsbaumverfahren (Decision Tree) zählt, zerlegen eine Datenmenge iterativ oder rekursiv mit dem Ziel, die Zielwerte (Klassen) im Rahmen des Lernens (Trainingsphase des überwachten Lernens) möglichst gut zu bereiningen, also eindeutige Klassenzuordnungen für bestimmte Eigenschaften in den Features zu erhalten. Die Zerlegung der Daten erfolgt über einen Informationsgewinn, der für die Klassifikation mit einem Maß der Unreinheit berechnet wird (im nächsten Artikel der Serie werden wir die Entropie berechnen!)

Die Entropie als Maß für Unreinheit in Daten

Die Entropie gilt als das am häufigsten eingesetzte Maß für Unreinheit (Impurity) in der Informatik. Es wird in ähnlicher Bedeutung auch in der Thermodynamik und Fluiddynamik eingesetzt, bezieht sich dort nicht auf Daten, sondern auf die Verteilung von Temperatur-/Gas-/Flüssigkeitsgemischen. Stellt man sich beispielsweise ein KiBa-Getränk (Kirsch-Banane-Mischung) vor, ist die Reinheit hoch, wenn man ein zweifarbiges Getränkt vor sich sieht (z. B. unten gelb, oben rot). Die Unreinheit ist hoch, ist das Getränkt gut vermischt, so dass keine zwei Farben mehr zu unterscheiden sind.

In der maschinellen Klassifikation bevorzugen wir Reinheit, denn je unterscheidbarer zwei (bzw. mehrere) Klassen, desto sicherer wird die Klassifikation. Somit müssen wir auch die Daten hinsichtlich ihrer Un-Reinheit bewerten können, was wir mit der Entropie im Sinne der Informatik tun:

Bei zwei zu separierenden Klassen demnach:

In Python umgesetzt könnte der Algorithmus beispielsweise so umgesetzt werden:

import math as math

def entropy(p):

    return - p * math.log2(p) - (1-p) * math.log2(1 - p)   

Die Entropie ist maximal (bei zwei Klassen: 1.00), wenn die Klassen innerhalb einer Obermenge gleich häufig sind. Gewinnt eine Klasse eine quantitative Dominanz, steigt die Wahrscheinlichkeit für diese Klasse gleichermaßen an, die Entropie sinkt. Entropie, als Maß für die Unreinheit, funktioniert mathematisch nur mit Wahrscheinlichkeiten größer 0 und kleiner 1, was wir abfangen sollten:

def entropy(p):

    if p > 1.0 or p <= 0.0:
        
        return 0
    
    else:
    
        return - p * math.log2(p) - (1-p) * math.log2(1 - p)   

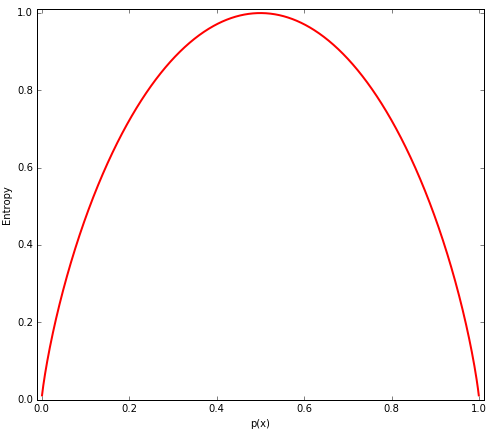
Schauen wir uns die Entropie nun einmal visuell an:

import numpy as np import matplotlib.pyplot as plt x = np.arange(0.0, 1.0, 0.001) ent = [entropy(p) for p in x] fig = plt.figure(figsize=(8,7)) ax = plt.subplot(111) ax.plot(x, ent, color = 'red', lw = 2) plt.ylim([0, 1.01]) plt.xlim([-0.01, 1.01]) plt.xlabel('p(x)') plt.ylabel('Entropy') plt.show()

Der Gini-Koeffizient als Maß für Unreinheit

Der Gini-Koeffizient funktioniert ähnlich wie die Entropie und nimmt sein Maximum bei exakt gleichhäufigen Klassen an, das bei 0.5 liegt. Der Gini-Koeffizient hat also gegenüber der Entropie ein flacheres degressives Wachstum, reagiert demnach etwas unempfindlicher auf Änderungen in Klassenhäufigkeiten.

In Python:

def gini(p):
    q = 1 - p
    return p * q+ (1 - p) * (1 - ( 1 - p))

Der Klassifikationsfehler als Maß für die Unreinheit

Noch unempfindlicher auf Änderungen in den Klassenhäufigkeiten (= Klassenwahrscheinlichkeiten) ist der Klassifikationsfehler:

In Python:

def error(p):
    return 1 - np.max([p, 1 - p])

Der Klassifikationsfehler sollte, insbesondere bei Mehrfachklassifikation, nicht zur Konstruktion für Entscheidungsbäume verwendet werden, ist aber das empfohlene Maß für das nachträgliche Stutzen (Pruning) der Baumzweige (Entscheidungsbäume neigen zur großen komplexen Modellen und zum Overfitting, was durch Pruning korrigiert werden kann).

Impurity – Bringing it all together

Bringen wir nun Entropie, Gini-Koeffizient und Klassifikationsfehler in eine gemeinsame Darstellung:

 
x = np.arange(0.0, 1.0, 0.001)

ent = [entropy(p) for p in x]

ent_scaled = [e * 0.5 for e in ent]

err = [error(i) for i in x]

fig = plt.figure(figsize=(8,7))
ax = plt.subplot(111)


for i, lab, ls, c, in zip ([ent, ent_scaled, gini(x), err], 
                            ['Entropie', 'Entropie (skaliert)', 'Gini-Koeffizient', 'Klassifizierungsfehler'], 
                            ['-', '-', '--', '-.'], 
                            ['red', 'orange', 'black', 'black']):
    line = ax.plot(x, i, label = lab, linestyle = ls, lw = 2, color = c)

ax.legend(loc='upper center', bbox_to_anchor=(0.5, 1.30), ncol = 3)
ax.axhline(y = 0.5, linewidth = 1, color = 'k', linestyle = '--')
ax.axhline(y = 1.0, linewidth = 1, color = 'k', linestyle = '--')
plt.ylim([0, 1.01])
plt.xlim([-0.01, 1.01])
plt.xlabel('p(x)')
plt.ylabel('Entropy')
plt.show()

Neben der “normalen” Entropie haben wir auch die skalierte Entropie (= Entropie / 2) eingefügt, um aufzuzeigen, dass die Steigung der Entropie gegenüber dem Gini-Koeffizienten deutlich stärker ist.

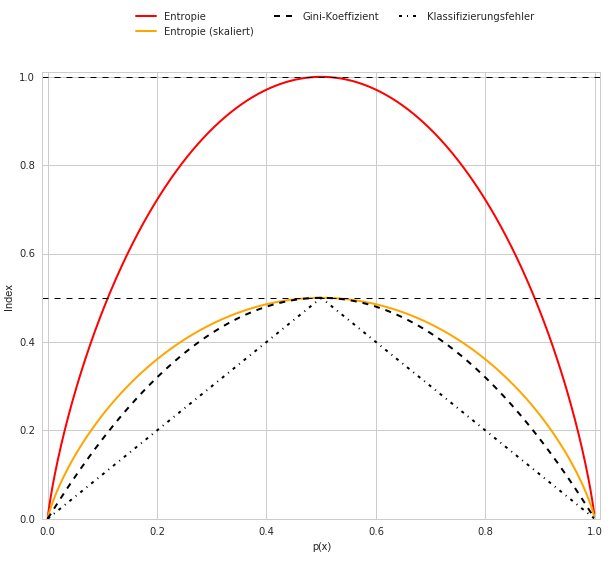
Auffällig ist auch, dass der Klassifikationsfehler (in der Darstellung als Dreieck sichtbar) gegenüber der Entropie und auch dem Gini-Koeffizienten deutlich unempfindlicher, in einem zwei-Klassen-System nämlich linear, auf Änderungen in den Klassenhäufigkeiten reagiert.

Literatur-Hinweise

Folgende Bücher bieten gute Grundlagen des Machine Learning und erläutern auch das Entscheidungsbaumverfahren:

Einführung in Data Science: Grundprinzipien der Datenanalyse mit Python	Data Science for Business: What you need to know about data mining and data-analytic thinking
R for Data Science	Machine Learning mit Python: Das Praxis-Handbuch für Data Science, Predictive Analytics und Deep Learning (mitp Professional)

About Author

Benjamin Aunkofer

Benjamin Aunkofer ist Gründer von DATANOMIQ und Hochschul-Dozent für Data Science und Data Strategy. Darüber hinaus arbeitet er als Interim Head of Business Intelligence und gibt Seminare/Workshops zu den Themen BI, Data Science und Machine Learning für Unternehmen.

See author's posts