Die Rastrigin-Funktion
Jeder Data Scientist kommt hin und wieder mal in die Situation, einen Algorithmus trainieren bzw. optimieren zu wollen oder zu müssen, ohne jedoch, dass passende Trainingsdaten unmittelbar verfügbar wären. Zum einen kann man in solchen Fällen auf Beispieldaten zugreifen, die mit vielen Analysetools mitgeliefert werden, oder aber man generiert sich seine Daten via mathematischer Modelle selbst, die für bestimmte Eigenschaften bekannt sind, die gute Bedingungen für das Optimierungstraining liefern.
Ein solches Modell, das man als Machine Learning Entwickler kennen sollte, ist die Rastrigin-Funktion, die laut Wikipedia von Leonard A. Rastrigin erstmalig beschrieben wurde. Dabei handelt es sich um eine Häufigkeites-/Wahrscheinlichkeitsverteilung, deren Dichte mehrere lokale Modi (Gipfel) aufweist. Ein Modus (oder Modalwert) ist in einer Häufigkeitsverteilung der häufigste Wert (“Bergspitze”) bzw. der Wert mit der höchsten Wahrscheinlichkeit.
Anmerkung des Autors: Dieser Artikel stellt zum einen die Rastrigin-Funktion und ihre Bedeutung für die Optimierungsrechnung vor, ist zum anderen aber auch eine Einführung in den Umgang mit NumPy-Matrizen (die eine Menge For-Schleifen ersparen können).
Die Rastrigin-Funktion
Mathematisch beschrieben wird die Rastrigin-Funktion wie folgt:
![]()
![]()
Wobei für das globale Minimum gilt: ![]()
Außerdem ist zu beachten, dass ![]() eine Konstante ist.
eine Konstante ist.
Die Rastrigin-Funktion im Standard-Python umsetzen und visualisieren
Die Formel lässt sich in Python (wie natürlich in jeder anderen Programmiersprache auch) einfach umsetzen:
value = 10 + x**2 - 10 * math.cos(2 * math.pi * x)
Nun können wir über den klassischen Weg der Programmierung einfach eine For-Schleife verwenden, um die Rastrigin-Funktionswerte in eine Liste zu packen und mit einem Plot zu visualsieren, dabei bin ich leider doch nicht ganz um die Verwendung des NumPy-Pakets nicht herumgekommen:
import matplotlib.pyplot as pyplot import numpy as np # NumPy hat die Matrizen-Datenstruktur, die wir benötigen import math as math # Grundlegende mathematische Funktionen (hier benötigt: Kreiszahl Pi und Cosinus-Funktion) rastriginValues = [] i = 0 for x in np.arange(-5.12, 5.12, 0.01): # Die Python-eigene range()-Funktion kann leider keine Floats, sondern nur Integer erzeugen :-/ value = 10 + x**2 - 10 * math.cos(2 * math.pi * x) i += 1 print(i, x, value) rastriginValues.append(value) pyplot.plot(rastriginValues) pyplot.ylim(0,50) pyplot.xlim(0,1024) pyplot.show()

Die grafische Darstellung zeigt, dass es sich tatsächlich um eine symmetrische multimodalen Verteilung handelt.
Die Rastrigin-Funktion mehrdimensional umsetzen, mit NumPy-Matrizen-Funktionen
Die obige Umsetzung der Rastrigin-Funktion ist eindimensional (eine Variable), braucht für die Darstellung allerdings zwei Dimensionen (f(x) und die Durchlaufanzahl bzw. Zeitachse). Nun könnten wir die Zahl der Variablen von 1 (x) auf 2 (x und y) erhöhen und eine dreidimensionale Darstellung erzeugen. Eine ähnliche dreidimensionale Darstellung gab es bereits in meiner Vorstellung des k-nearest-Neighbour-Algorithmus nachzuvollziehen. Dabei müssten wir die Konstante ![]() auf
auf ![]() verdoppeln:
verdoppeln:
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as pyplot
import numpy as np
figure = pyplot.figure()
axe = figure.add_subplot(111, projection='3d')
x = np.linspace(-5.12, 5.12, 100) # unterteilt den Bereich in 100 Schnitte, ähnlich: np.arange(-5.12, 5.12, 0.1)
y = np.linspace(-5.12, 5.12, 100)
x, y = np.meshgrid(x, y) # erzeugt ein Koordinatensystem
# Nun ohne Schleifen: Wir wenden die NumPy-Funktionen (np.cos statt math.cos und np.pi statt math.pi)
# auf die NumPy-Arrays an (x und y) und erhalten ein NumPy-Array z zurück
z = 20 + x**2 - 10 * np.cos(2 * np.pi * x) + y**2 - 10 * np.cos(2* np.pi * y)
# Plotte die drei Variablen (x, y, z) im dreidimensionalen Raum
axe.plot_surface(x, y, z, rstride=1, cstride=1, cmap="jet", linewidth=0, antialiased=False)
pyplot.title('Rastrigin-Map')
pyplot.grid(True)
axes = pyplot.gca()
axes.set_xlim([-5.12,5.12])
axes.set_ylim([-5.12,5.12])
pyplot.show()
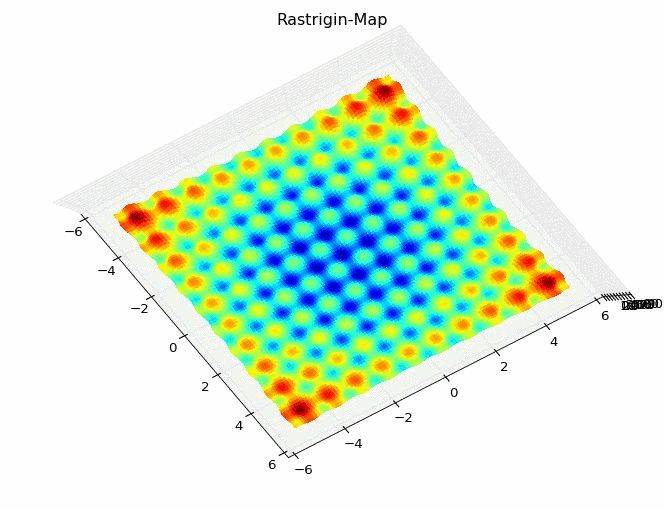
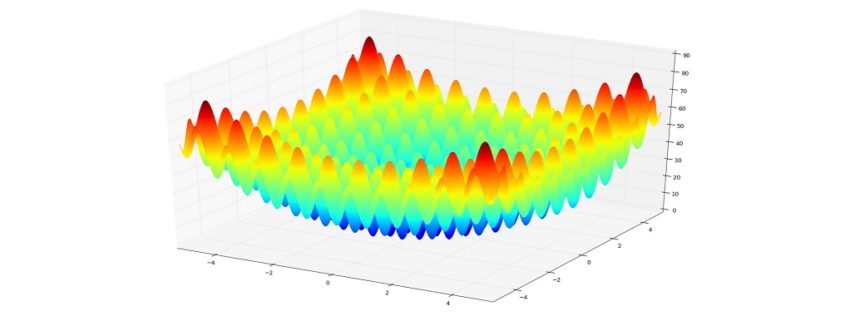
Die Rastrigin-Funktion wird gerne für Optimierungsalgorithmen eingesetzt, wofür sie wegen des großen Suchraums und der hohen Anzahl lokaler Modi ein herausforderndes Umfeld bietet. Beispielsweise wird – meines Erachtens nach – das wohl beliebteste Optimierungsverfahren im maschinellen Lernen, das Gradientenverfahren, hier keine guten Ergebnisse liefern, denn es gibt einfach zu viele lokale Minima.





Leave a Reply
Want to join the discussion?Feel free to contribute!