Mathematik Archives

Tag Archive for: Mathematik

Die Rastrigin-Funktion

September 15, 2016/in Mathematik, Optimierungsverfahren, Python, Tutorial, Visualization/by Benjamin Aunkofer

Jeder Data Scientist kommt hin und wieder mal in die Situation, einen Algorithmus trainieren bzw. optimieren zu wollen oder zu müssen, ohne jedoch, dass passende Trainingsdaten unmittelbar verfügbar wären. Zum einen kann man in solchen Fällen auf Beispieldaten zugreifen, die mit vielen Analysetools mitgeliefert werden, oder aber man generiert sich seine Daten via mathematischer Modelle selbst, die für bestimmte Eigenschaften bekannt sind, die gute Bedingungen für das Optimierungstraining liefern.

Ein solches Modell, das man als Machine Learning Entwickler kennen sollte, ist die Rastrigin-Funktion, die laut Wikipedia von Leonard A. Rastrigin erstmalig beschrieben wurde. Dabei handelt es sich um eine Häufigkeites-/Wahrscheinlichkeitsverteilung, deren Dichte mehrere lokale Modi (Gipfel) aufweist. Ein Modus (oder Modalwert) ist in einer Häufigkeitsverteilung der häufigste Wert (“Bergspitze”) bzw. der Wert mit der höchsten Wahrscheinlichkeit.

Anmerkung des Autors: Dieser Artikel stellt zum einen die Rastrigin-Funktion und ihre Bedeutung für die Optimierungsrechnung vor, ist zum anderen aber auch eine Einführung in den Umgang mit NumPy-Matrizen (die eine Menge For-Schleifen ersparen können).

Die Rastrigin-Funktion

Mathematisch beschrieben wird die Rastrigin-Funktion wie folgt:

$f(x_1 cdots x_n) = An + sum_{i=1}^n (x_i^2 -10cos(2pi x_i))$

$-5.12 leq x_i leq 5.12$

Wobei für das globale Minimum gilt: $f(0) = 0$
Außerdem ist zu beachten, dass $A=10$ eine Konstante ist.

Die Rastrigin-Funktion im Standard-Python umsetzen und visualisieren

Die Formel lässt sich in Python (wie natürlich in jeder anderen Programmiersprache auch) einfach umsetzen:

value = 10 + x**2 - 10 * math.cos(2 * math.pi * x)

Nun können wir über den klassischen Weg der Programmierung einfach eine For-Schleife verwenden, um die Rastrigin-Funktionswerte in eine Liste zu packen und mit einem Plot zu visualsieren, dabei bin ich leider doch nicht ganz um die Verwendung des NumPy-Pakets nicht herumgekommen:

import matplotlib.pyplot as pyplot
import numpy as np # NumPy hat die Matrizen-Datenstruktur, die wir benötigen 
import math as math # Grundlegende mathematische Funktionen (hier benötigt: Kreiszahl Pi und Cosinus-Funktion)

rastriginValues = []
i = 0


for x in np.arange(-5.12, 5.12, 0.01): # Die Python-eigene range()-Funktion kann leider keine Floats, sondern nur Integer erzeugen :-/
    value = 10 + x**2 - 10 * math.cos(2 * math.pi * x)
    i += 1
    print(i, x, value)
    rastriginValues.append(value)
    
pyplot.plot(rastriginValues)
pyplot.ylim(0,50)
pyplot.xlim(0,1024)
pyplot.show()

Die grafische Darstellung zeigt, dass es sich tatsächlich um eine symmetrische multimodalen Verteilung handelt.

Die Rastrigin-Funktion mehrdimensional umsetzen, mit NumPy-Matrizen-Funktionen

Die obige Umsetzung der Rastrigin-Funktion ist eindimensional (eine Variable), braucht für die Darstellung allerdings zwei Dimensionen (f(x) und die Durchlaufanzahl bzw. Zeitachse). Nun könnten wir die Zahl der Variablen von 1 (x) auf 2 (x und y) erhöhen und eine dreidimensionale Darstellung erzeugen. Eine ähnliche dreidimensionale Darstellung gab es bereits in meiner Vorstellung des k-nearest-Neighbour-Algorithmus nachzuvollziehen. Dabei müssten wir die Konstante $A=10$ auf $A=20$ verdoppeln:

from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as pyplot
import numpy as np

figure = pyplot.figure()
axe = figure.add_subplot(111, projection='3d')

x = np.linspace(-5.12, 5.12, 100) # unterteilt den Bereich in 100 Schnitte, ähnlich: np.arange(-5.12, 5.12, 0.1)
y = np.linspace(-5.12, 5.12, 100)
x, y = np.meshgrid(x, y) # erzeugt ein Koordinatensystem

# Nun ohne Schleifen: Wir wenden die NumPy-Funktionen (np.cos statt math.cos und np.pi statt math.pi) 
# auf die NumPy-Arrays an (x und y) und erhalten ein NumPy-Array z zurück
z = 20 + x**2 - 10 * np.cos(2 * np.pi * x) + y**2 - 10 * np.cos(2* np.pi * y)

# Plotte die drei Variablen (x, y, z) im dreidimensionalen Raum
axe.plot_surface(x, y, z, rstride=1, cstride=1, cmap="jet", linewidth=0, antialiased=False)

pyplot.title('Rastrigin-Map')
pyplot.grid(True)
axes = pyplot.gca()
axes.set_xlim([-5.12,5.12])
axes.set_ylim([-5.12,5.12])
pyplot.show()

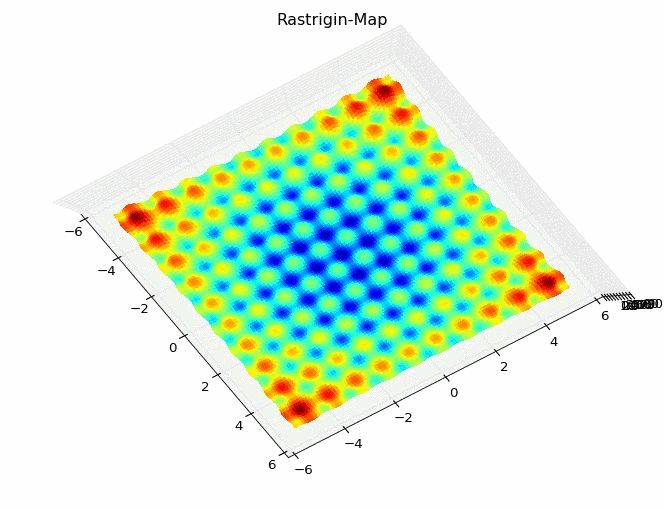
Die Rastrigin-Funktion wird gerne für Optimierungsalgorithmen eingesetzt, wofür sie wegen des großen Suchraums und der hohen Anzahl lokaler Modi ein herausforderndes Umfeld bietet. Beispielsweise wird – meines Erachtens nach – das wohl beliebteste Optimierungsverfahren im maschinellen Lernen, das Gradientenverfahren, hier keine guten Ergebnisse liefern, denn es gibt einfach zu viele lokale Minima.

Wahrscheinlichkeitesrechnung – Grundstein für Predictive Analytics

November 11, 2015/in Data Science, Mathematik, Predictive Analytics, Statistics/by Benjamin Aunkofer

Die Wahrscheinlichkeitsrechnung behandelt die Gesetzmäßigkeiten des (von außen betrachtet) zufälligen Vorkommens bestimmter Ereignisse aus einer vorgegebenen Ereignismenge. Die mathematische Statistik fasst diese Wahrscheinlichkeitsrechnung zur Stochastik zusammen, der Mathematik des Zufalls.

Mit diesem Artikel – zu der ich eine Serie plane – möchte ich den Einstieg in Predictive Analytics wagen, zugegebenermaßen ein Themengebiet, in dem man sich sehr schnell verlieren und den Wald vor lauter Bäumen nicht mehr findet. Also belassen wir es erstmal bei einem sanften Einstieg…

Klassische Definition der Wahrscheinlichkeit

Das klassische Verständnis der Wahrscheinlichkeit geht von endlich vielen Ausgängen (Ereignisse) aus, bei denen alle Ausgänge gleich wahrscheinlich sind. Die dafür erdachten Zufallsexperimente wurden von dem französischen Mathematiker Pierre Simon Lapplace (1749 – 1827) zum ersten Mal nachvollziehbar beschrieben. Diese Zufallsexperimente werden daher auch Laplace-Experimente genannt.

Bei einem Laplace Experiment gilt:

Ereignismenge $Omega = {omega_1,omega_2,omega_3,…omega_s}$
Wahrscheinlichkeit $p(w_j)=frac{1}{s}=frac{1}{|Omega|}$
$(j=1,2,3,…s)$

Die Ergebnismenge, das ist die Menge aller möglichen Ereignisse, wird in der Regel mit einem $Omega$ (Omega) gekennzeichnet, ein beliebiges Einzelereignis hingegen als $omega$ (kleines Omega).

Eine typische Laplace-Wahrscheinlichkeitsfrage ist ein bevorstehender Würfelwurf. Wie groß ist die Wahrscheinlichkeit, mit einem echten (unverfälschten) Würfel eine gerade Zahl zu würfeln?

Mit $Omega={1,2,3,4,5,6}$ und $A={2,4,6}$ folgt $P(A)=frac{|A|}{|Omega|}=frac{3}{6}=0,5$ .

Axiomatische Definition der Wahrscheinlichkeit

Jeder Wahrscheinlichkeitsbegriff muss auf denselben äußeren Bedingungen beruhenden Zufallsexperimenten beliebig oft wiederholbar sein. Die axiomatische Definition der Wahrscheinlichkeit P(A) eines Ereignisses A berücksichtigt Axiome. Axiome sind nicht beweisbare Grundpostulate, darunter fallen Gegebenheiten, die gewissermaßen unverstanden sind und deren Vorkommen und Bedeutung in der Regel empirisch belegt werden müssen.
Die Definition der axiomatischen Wahrscheinlichkeit stammt vom russischen Mathematiker Andrej Nikollajewitsch Kolmogorov (1903 – 1987).

In der Realität gibt es keine perfekte Zufälligkeit, denn jedes Ergebnis ist von ganz bestimmten Faktoren abhängig. Auf den Würfelwurf bezogen, hängt das gewürfelte Ergebnis von unüberschaubar vielen Faktoren ab. Wären diese alle bekannt, könnte das Ergebnis exakt berechnet und somit mit einer Sicherheit vorhergesagt werden. Da dafür jedoch in der Praxis unbestimmbar viele Faktoren eine Rolle spielen (beispielsweise die genaue Beschaffenheit des Würfels in Form, Gewicht, Materialwiderstand, der genaue Winkel, die Fallgeschwindigkeit, die Ausgangsposition der Hand und des Würfels) können wir das Ergebnis nur schätzen, indem die Beschreibung des Vorgangs vereinfacht wird. Nur diese Vereinfachung macht es uns möglich, Vorhersagen zu treffen, die dann jedoch nur eine Wahrscheinlichkeit darstellen und somit mit einer Unsicherheit verbunden sind.

In der abstrakten Welt des perfekten Zufalls gäbe es die gleiche Chance, eine “4” zu würfeln, wie jeweils alle anderen Ziffern.

Mit $Omega={1,2,3,4,5,6}$ und $A={4}$ folgt $P(A)=frac{|A|}{|Omega|}=frac{1}{6}=0,167$ .

Das Ergebnis eines Wurfes des Würfels ist in der Realität auch von der Beschaffenheit des Würfels abhängig. Angenommen, der Würfel hat auf Seite der Ziffer “4” bei allen vier Kanten eine Abrundung, die ein Umkippen auf eine andere Seite begünstigen, so bedeutet dies:

Die Ziffer “4” hat vier abgerundete Kanten, die Wahrscheinlichkeit eine “4” zu würfeln sinkt stark
Die Ziffern “1”, “3”, “5”, “6” haben jeweils eine abgerundete Kante (Berühungskante zur “4”) sinkt
Die Ziffer “2” liegt der “4” gegenüber, hat somit keine Berührungskante und keine Abrundung, so steigt ihre Chance gewürfelt zu werden

Nun könnte sich nach einer empirischen Untersuchung mit einer ausreichenden Stichprobe folgende Wahrscheinlichkeit ergeben:

$p(4) = 0,1$
$p(1) = p(3) = p(5) = p(6) = 0,15$
$p(2) = 0,3$
$P(Omega) = 1,0$

Durch die Analyse der bisherigen Wurf-Historie und der Betrachtung der Beschaffenheit der Kanten des Würfels können wir uns somit weit realistischere Wahrscheinlichkeiten über die Wurfergebnisse ermitteln. Wie hoch wäre nun die Wahrscheinlichkeit, nach einem Wurf eine gerade Zahl zu würfeln?

Mit $Omega={1,2,3,4,5,6}$ und $A={2,4,6}$ folgt $P(A)=p(2)+p(4)+p(6)=0,55$ .

Wie lernen Maschinen?

October 30, 2015/in Big Data, Data Mining, Machine Learning, Optimierungsverfahren/by Dr. Stefan Kühn

Im zweiten Teil wollen wir das mit Abstand am häufigsten verwendete Optimierungsverfahren – das Gradientenverfahren oder Verfahren des steilsten Abstiegs – anhand einiger Beispiele näher kennen lernen. Insbesondere werden wir sehen, dass die Suchrichtung, die bei der Benennung der Verfahren meist ausschlaggebend ist, gar nicht unbedingt die wichtigste Zutat ist.

Wie lernen Maschinen?

October 13, 2015/in Big Data, Data Science, Machine Learning, Optimierungsverfahren, Statistics/by Dr. Stefan Kühn

Machine Learning ist eines der am häufigsten verwendeten Buzzwords im Data-Science- und Big-Data-Bereich. Aber lernen Maschinen eigentlich und wenn ja, wie? In den meisten Fällen lautet die Antwort: Maschinen lernen nicht, sie optimieren. Fällt der Begriff Machine Learning oder Maschinelles Lernen, so denken viele sicherlich zuerst an bekannte “Lern”-Algorithmen wie Lineare Regression, Logistische Regression, Neuronale Netze oder Support Vector Machines. Die meisten dieser Algorithmen – wir beschränken uns hier vorerst auf den Bereich des Supervised Learning – sind aber nur Anwendungen einer anderen, grundlegenderen Theorie – der mathematischen Optimierung. Alle hier angesprochenen Algorithmen stellen dem Anwender eine bestimmte Ziel- oder Kostenfunktion zur Verfügung, aus der sich i.a. der Name der Methode ableitet und für die im Rahmen des Lernens ein Minimum oder Optimum gefunden werden soll. Ein großer Teil des Geheimnisses und die eigentliche Stärke der Machine-Learning-Algorithmen liegt nun darin, dass dieser Minimierungsprozess effizient durchgeführt werden kann. Wir wollen im Folgenden kurz erklären, wie dies in etwa funktioniert. In einem späteren Blogpost gehen wir dann genauer auf das Thema der Effizienz eingehen. Read more

Tag Archive for: Mathematik

Die Rastrigin-Funktion

Die Rastrigin-Funktion

Die Rastrigin-Funktion im Standard-Python umsetzen und visualisieren

Die Rastrigin-Funktion mehrdimensional umsetzen, mit NumPy-Matrizen-Funktionen

Wahrscheinlichkeitesrechnung – Grundstein für Predictive Analytics

Klassische Definition der Wahrscheinlichkeit

Axiomatische Definition der Wahrscheinlichkeit

Wie lernen Maschinen?

Wie lernen Maschinen?

Interesting links

Pages

Categories

Archive