Neuronale Netzwerke zur Spam-Erkennung
Die Funktionsweise der in immer mehr Anwendungen genutzten neuronalen Netzwerke stieß bei weniger technik-affinen Menschen bislang nur auf wenig Interesse. Geschuldet wird das sicher vor allem der eher trockenen Theorie, die hinter diesen Konstrukten steht und die sich für die meisten nicht auf Anhieb erschließt. Ein populäres Beispiel für die Fähigkeiten, die ein solches neuronales Netzwerk bereits heute hat, lieferte in jüngster Zeit Googles “Inception”, welches ohne den Anspruch auf einen praktischen Nutzen eigenständig eine spektakuläre Bilderwelt kreierte, die auch Menschen ohne großes Interesse an den dahinter steckenden Technologien ins Staunen versetzte. Ansonsten bieten sich die neuronalen Netze vor allem überall dort an, wo wenig systematisches Wissen zur Verfügung steht, wie etwa bei der Bilderkennung und der Text- bzw. Sprachanalyse.
Weniger effektheischend, als die Ergebnisse von “Inception”, dafür jedoch überaus hilfreich für den vernetzten Alltag, sind neuronale Netzwerke, die zum Aufspüren und zur Kategorisierung von Spam-Seiten entwickelt werden. In diesem Anwendungsbereich können diese ein wertvolles Werkzeug sein.
Wie bei allen selbstlernenden Netzwerken muss dafür zunächst ein Grundgerüst aufgebaut werden, welches später von Hand mit Informationen gefüttert wird, bis es schließlich in der Lage ist, sich selbstständig weiter zu entwickeln, hinzuzulernen und auf diese Weise immer genauere Ergebnisse liefert.
Die Auswahl der Kriterien
Unerwünschte Webseiten mit störenden und oft illegalen Inhalten findet man im Internet zu Hauf und meist locken sie mit dubiosen Angeboten für vermeintliche Wundermittel oder gaukeln leichtgläubigen Nutzern vor, man könne ohne großes Zutun viel Geld verdienen – meist ohne ein tatsächliches Produkt oder eine Dienstleistung dahinter. Ein entsprechend programmiertes neuronales Netzwerk spürt diese Seiten anhand von bestimmten Faktoren automatisch auf. Als Trainingsdaten werden dafür zunächst von Hand Kriterien wie die Registrierungs-IP, der Nutzername und die verwendete Sprachversion eingegeben. Da das Netzwerk nur mit den Zahlen 0 und 1 arbeiten kann, müssen diese Datensätze zuvor manuell aufbereitet werden. Indem alle gewünschten Registrierungs-IPs erst auf den jeweiligen Internetdienstanbieter abgebildet werden und der Grad ihrer jeweiligen Spammigkeit von Hand bestimmt wird, lässt sich der jeweilige Durchschnitt der “Spammigkeit” eines Internetdienstanbieters berechnen. Teilt man die Anzahl der Spammer durch die Gesamtnutzerzahl eines einzelnen Anbieters, erhält man bereits ein Ergebnis, das sich zur Eingabe in das neuronale Netzwerk eignet. Ähnlich kann z. B. bei der Kombination aus Geolocation und Sprachversion verfahren werden. Mit einer Vielzahl weiterer Faktoren kann die Effizienz des neuronalen Netzwerks verbessert werden. So lassen sich etwa große Unterschiede bei dem Herkunftsland feststellen, in dem die Spam-Seiten angesiedelt sind. Ein besonders großes Erkennungspotential bieten bestimmte Keywords und Keyword-Kombinationen, die mitunter eindeutige Rückschlüsse auf ein Spam-Angebot ziehen lassen. Befindet sich z. B. die Wortkombination “Geld verdienen” besonders häufig auf einer Seite, ist dies ein recht deutliches Kriterium für die Klassifizierung als Spam. Doch auch weniger offensichtliche Faktoren helfen dem neuronalen Netzwerk dabei, hellhörig zu werden: Ein ungewöhnliches Verhältnis zwischen Vokalen und Konsonanten oder auch Seitennamen, die vermehrt Zahlen und unübliche Zeichen beinhalten, können die Spam-Wahrscheinlichkeit steigern. Kommt die verwendete IP-Adresse aus einem anonymisierten Netzwerk oder VPN, schürt dies ebenfalls den Verdacht auf unseriöse Inhalte.
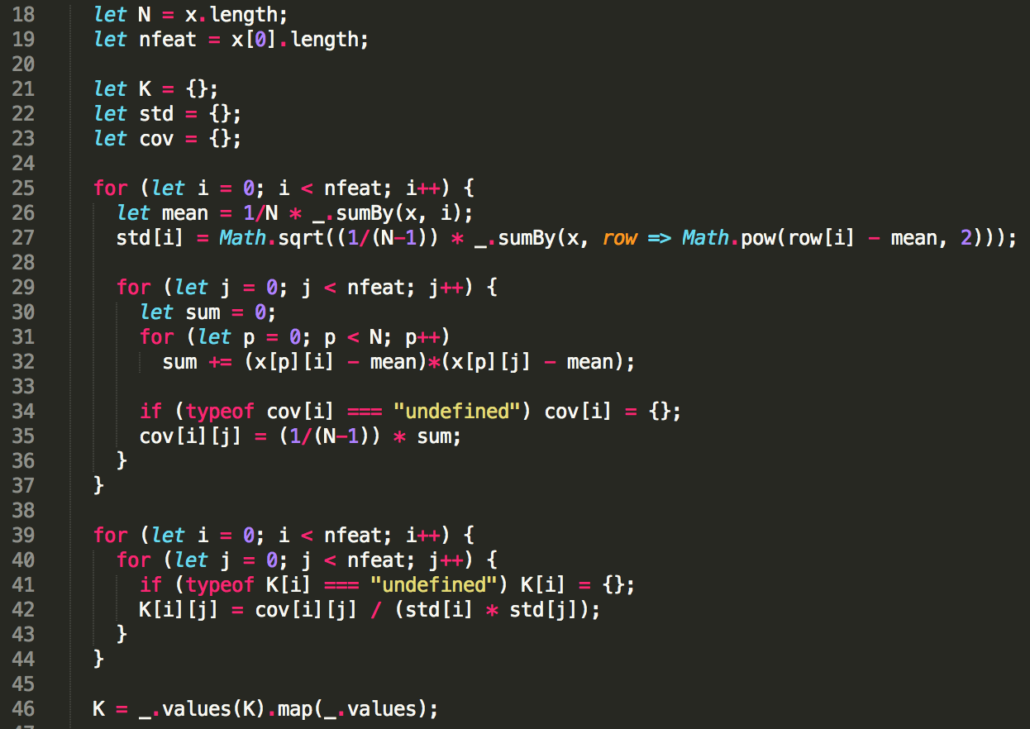
Erstellung einer Korrelationsmatrix
Da jedes der einbezogenen Kriterien zur Bestimmung der Spammigkeit einer Seite eine unterschiedlich hohe Relevanz hat, müssen die einzelnen Faktoren verschieden stark gewichtet werden. Damit das neuronale Netzwerk genau das tun kann, wird deshalb eine Korrelationsmatrix erstellt. In dieser Matrix werden alle gesammelten Kriterien in Verbindung zueinander gesetzt, um es dem Netzwerk zu ermöglichen, nicht jeden Punkt nur einzeln zu werten. So ist ein Keyword wie z. B. “100 mg” an sich vergleichsweise unverdächtig. Stammt die Seite, auf der das Wort vorkommt jedoch aus einer Gegend, in der erfahrungsgemäß viele unseriöse Arzneimittelanbieter angesiedelt sind, kann dies die Spam-Wahrscheinlichkeit erhöhen.
Libraries für die Implementierung
Ein wertvolles Tool, das sich für die Implementierung des jeweiligen neuronalen Netzwerks eignet, ist die Open Source Machine Learning Library “Tensor Flow” von Google. Diese Programmierschnittstelle der zweiten Generation verfügt über einige handfeste Vorteile gegenüber anderen Libraries und ermöglicht die Parallelisierung der Arbeit. Berechnet wird sie auf der schnellen GPU des Rechners, was in direkten Vergleichen die Rechenzeit um ein Vielfaches senken konnte. Bewährt hat sich “Tensor Flow” bereits in zahlreichen kommerziellen Diensten von Google, darunter Spracherkennungssoftware, Google Photos, und Gmail.
Für eine bessere Abstraktion des Netzwerks, können zusätzlich zu der hinteren mehrere weitere Schichten angelegt werden. Die hintere Schicht bleibt dabei oft die einzige, die von außerhalb sichtbar ist.
Die Optimierung des neuronalen Netzwerks
Es liegt in der Natur der Sache, dass ein eigenständig lernfähiges Netzwerk nicht von Anfang an durch höchste Zuverlässigkeit hinsichtlich seiner Trefferquote besticht. Zum Lernen gehört Erfahrung und die muss das Netz erst noch sammeln. Zwar gelingt es auch einem noch frisch programmierten Netzwerk bereits die Erfüllung seiner Aufgabe oft recht gut, die Fehlerquote kann jedoch im Laufe der Zeit immer weiter verbessert werden. Gerade am Anfang werden noch viele Spam-Seiten nicht erkannt und einige vermeintliche Spammer stellen sich bei der Überprüfung durch den Menschen als unbedenklich heraus. Darum ist es für die Steigerung der Effizienz praktisch unerlässlich, immer wieder von Hand einzugreifen, falsche Ergebnisse zu korrigieren und dem Netzwerk auf diese Weise zu helfen.



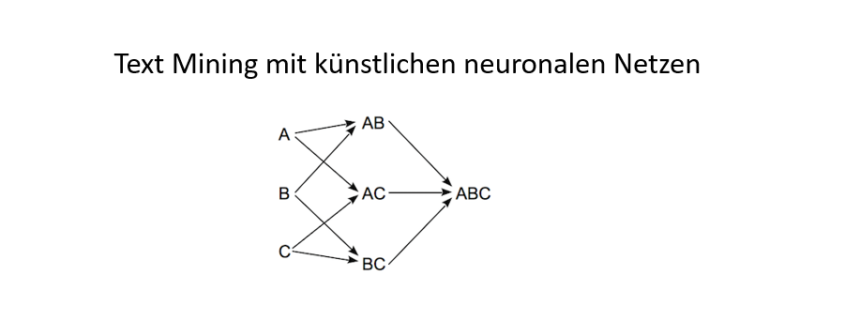
 ndgedanke dabei ist es, dass Neuronen entsprechend höher gewichtet werden sollten, wenn sie mit anderen hoch gewichteten Neuronen in Beziehung stehen. Wenn also beispielsweise eine Silbe in vielen hoch gewichteten Worten auftaucht, wird sie selbst entsprechend höher gewichtet.
ndgedanke dabei ist es, dass Neuronen entsprechend höher gewichtet werden sollten, wenn sie mit anderen hoch gewichteten Neuronen in Beziehung stehen. Wenn also beispielsweise eine Silbe in vielen hoch gewichteten Worten auftaucht, wird sie selbst entsprechend höher gewichtet.


