Maschinelles Lernen (Machine Learning) ist eine Gebiet der Künstlichen Intelligenz (KI, bzw. AI von Artificial Intelligence) und der größte Innovations- und Technologietreiber dieser Jahre. In allen Trendthemen – wie etwa Industrie 4.0 oder das vernetzte und selbstfahrende Auto – spielt die KI eine übergeordnete Rolle. Beispielsweise werden in Unternehmen viele Prozesse automatisiert und auch Entscheidungen auf operativer Ebene von einer KI getroffen, zum Beispiel in der Disposition (automatisierte Warenbestellungen) oder beim Festsetzen von Verkaufspreisen.
Aufsehen erregte Google mit seiner KI namens AlphaGo, einem Algortihmus, der den Weltmeister im Go-Spiel in vier von fünf Spielen besiegt hatte. Das Spiel Go entstand vor mehr als 2.500 Jahren in China und ist auch heute noch in China und anderen asiatischen Ländern ein alltägliches Gesellschaftsspiel. Es wird teilweise mit dem westlichen Schach verglichen, ist jedoch einfacher und komplexer zugleich (warum? das wird im Google Blog erläutert). Machine Learning kann mit einer Vielzahl von Methoden umgesetzt werden, werden diese Methoden sinnvoll miteinander kombiniert, können durchaus äußerst komplexe KIs erreicht werden. Der aktuell noch gängigste Anwendungsfall für Machine Learning ist im eCommerce zu finden und den meisten Menschen als die Produktvorschläge von Amazon.com bekannt: Empfehlungsdienste (Recommender System).
Klassifikation via K-Nearest Neighbour Algorithmus
Ein häufiger Zweck des maschinellen Lernens ist, technisch gesehen, die Klassifikation von Daten in Abhängigkeit von anderen Daten. Es gibt mehrere ML-Algorithmen, die eine Klassifikation ermöglichen, die wohl bekannteste Methode ist der k-Nearest-Neighbor-Algorithmus (Deutsch:„k-nächste-Nachbarn”), häufig mit “kNN” abgekürzt. Das von mir interviewte FinTech StartUp Number26 nutzt diese Methodik beispielsweise zur Klassifizierung von Finanztransaktionen.
Um den Algorithmus Schritt für Schritt aufbauen zu können, müssen wir uns
Natürlich gibt es in Python, R und anderen Programmiersprachen bereits fertige Bibliotheken, die kNN bereits anbieten, denen quasi nur Matrizen übergeben werden müssen. Am bekanntesten ist wohl die scikit-learn Bibliothek für Python, die mehrere Nächste-Nachbarn-Modelle umfasst. Mit diesem Minimalbeispiel wollen wir den grundlegenden Algorithmus von Grund auf erlernen. Wir wollen also nicht nur machen, sondern auch verstehen.
Vorab: Verwendete Bibliotheken
Um den nachstehenden Python-Code (Python 3.x, sollte allerdings auch mit Python 2.7 problemlos funktionieren) ausführen zu können, müssen folgende Bibliotheken eingebunden werden:
import numpy as numpy
import matplotlib.pyplot as pyplot
from mpl_toolkits.mplot3d import Axes3D #Erweiterung für die Matplotlib - siehe: http://matplotlib.org/mpl_toolkits/
Übrigens: Eine Auflistung der wohl wichtigsten Pyhton-Bibliotheken für Datenanalyse und Datenvisualisierung schrieb ich bereits hier.
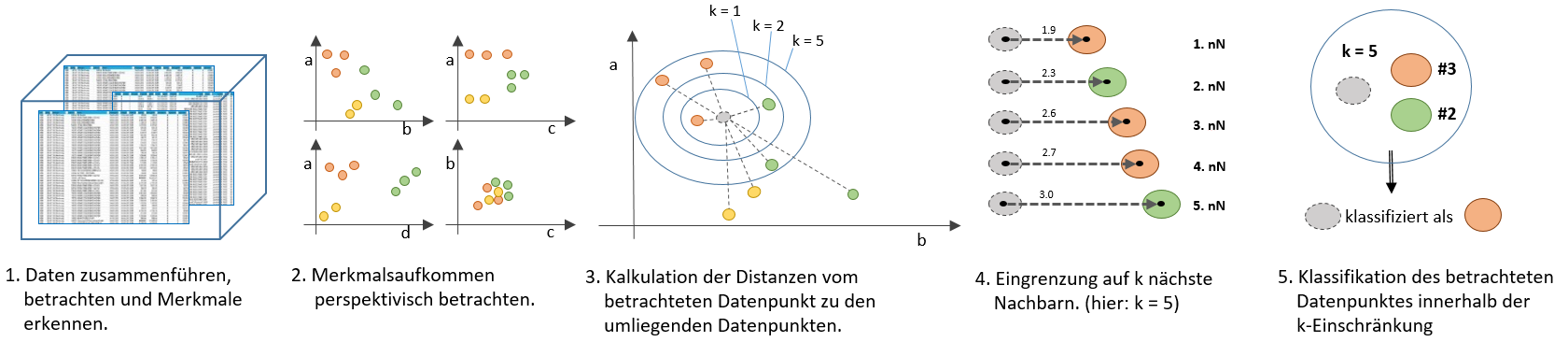
Schritt 1 – Daten betrachten und Merkmale erkennen
Der erste Schritt ist tatsächlich der aller wichtigste, denn erst wenn der Data Scientist verstanden hat, mit welchen Daten er es zu tun hat, kann er die richtigen Entscheidungen treffen, wie ein Algorithmus richtig abgestimmt werden kann und ob er für diese Daten überhaupt der richtige ist.
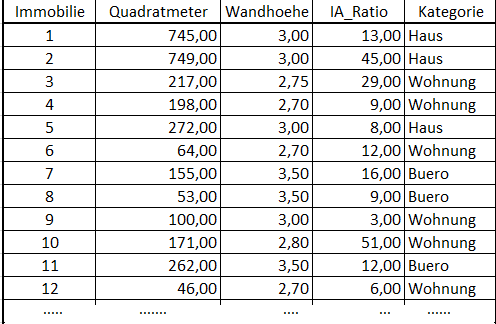
In der Realität haben wir es oft mit vielen verteilten Daten zu tun, in diesem Minimalbeispiel haben wir es deutlich einfacher: Der Beispiel-Datensatz enthält Informationen über Immobilien über vier Spalten.
- Quadratmeter: Größe der nutzbaren Fläche der Immobilie in der Einheit m²
- Wandhoehe: Höhe zwischen Fußboden und Decke innerhalb der Immobilie in der Einheit m
- IA_Ratio: Verhältnis zwischen Innen- und Außenflächen (z. B. Balkon, Garten)
- Kategorie: Enthält eine Klassifizierung der Immobilie als “Haus”, “Wohnung” und “Büro”
[box]Hinweis für Python-Einsteiger: Die Numpy-Matrix ist speziell für Matrizen-Kalkulationen entwickelt. Kopfzeilen oder das Speichern von String-Werten sind für diese Datenstruktur nicht vorgesehen![/box]
def readDataSet(filename):
fr = open(filename) # Datei-Stream vorbereiten
numberOfLines = len(fr.readlines()) # Anzahl der Zeilen ermitteln
returnMat = numpy.zeros((numberOfLines-1,3)) # Eine Numpy-Matrix in Höhe der Zeilenanzahl (minus Kopfzeile) und in Breite der drei Merkmal-Spalten
classLabelVector = [] # Hier werden die tatsächlichen Kategorien (Haus, Wohnung, Büro) vermerkt
classColorVector = [] # Hier werden die Kategorien über Farben vermerkt (zur späteren Unterscheidung im 3D-Plot!)
#print(returnMat) # Ggf. mal die noch die ausge-null-te Matrix anzeigen lassen (bei Python 2.7: die Klammern weglassen!)
fr = open(filename) # Datei-Stream öffnen
index = 0
for line in fr.readlines(): # Zeile für Zeile der Datei lesen
if index != 0: # Kopfzeile überspringen
line = line.strip()
listFromLine = line.split('\t') # Jede Zeile wird zur temporären Liste (Tabulator als Trennzeichen)
returnMat[index-1,:] = listFromLine[1:4] #Liste in die entsprechende Zeile der Matrix überführen
classLabel = listFromLine[4] # Kategorie (Haus, Wohnung, Büro) für diese Zeile merken
if classLabel == "Buero":
color = 'yellow'
elif classLabel == "Wohnung":
color = 'red'
else:
color = 'blue'
classLabelVector.append(classLabel) # Kategorie (Haus, Wohnung, Büro) als Text-Label speichern
classColorVector.append(color) # Kategorie als Farbe speichern (Büro = gelb, Wohnung = rot, Haus = Blau)
index += 1
return returnMat,classLabelVector, classColorVector
Aufgerufen wird diese Funktion dann so:
dataSet, classLabelVector, classColorVector = readDataSet("K-Nearst_Neighbour-DataSet.txt")
Die Matrix mit den drei Spalten (Quadratmeter, Wandhohe, IA_Ratio) landen in der Variable “dataSet”.
Schritt 2 – Merkmale im Verhältnis zueinander perspektivisch betrachten
Für diesen Anwendungsfall soll eine Klassifizierung (und gewissermaßen die Vorhersage) erfolgen, zu welcher Immobilien-Kategorie ein einzelner Datensatz gehört. Im Beispieldatensatz befinden sich vier Merkmale: drei Metriken und eine Kategorie (Wohnung, Büro oder Haus). Es stellt sich zunächst die Frage, wie diese Merkmale zueinander stehen. Gute Ideen der Datenvisualisierung helfen hier fast immer weiter. Die gängigsten 2D-Visualisierungen in Python wurden von mir bereits hier zusammengefasst.
[box]Hinweis: In der Praxis sind es selten nur drei Dimensionen, mit denen Machine Learning betrieben wird. Das Feature-Engineering, also die Suche nach den richtigen Features in verteilten Datenquellen, macht einen wesentlichen Teil der Arbeit eines Data Scientists aus – wie auch beispielsweise Chief Data Scientist Klaas Bollhoefer (siehe Interview) bestätigt.[/box]
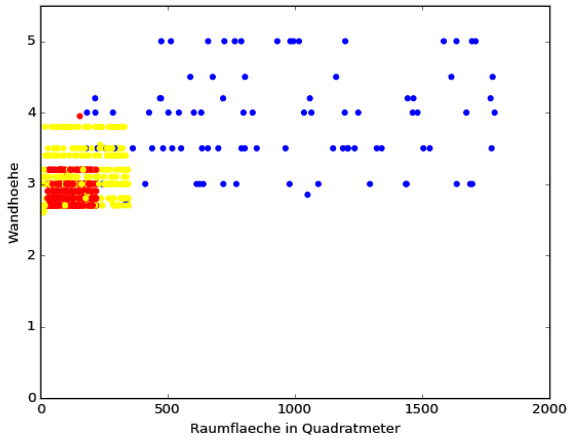 |
fig = pyplot.figure()
ax = fig.add_subplot(111)
ax.scatter(dataSet[:,0], dataSet[:,1], marker='o', color=classColorVector)
ax.set_xlabel("Raumflaeche in Quadratmeter")
ax.set_ylabel("Wandhohe")
ax.set_xlim(xmin=0)
ax.set_ylim(ymin=0)
pyplot.show()
|
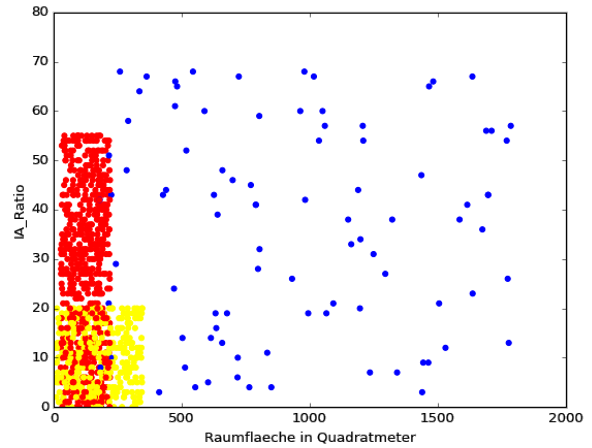 |
fig = pyplot.figure()
ax = fig.add_subplot(111)
ax.scatter(dataSet[:,0], dataSet[:,2], marker='o', color=classColorVector)
ax.set_xlabel("Raumflaeche in Quadratmeter")
ax.set_ylabel("IA_Ratio")
ax.set_xlim(xmin=0)
ax.set_ylim(ymin=0)
pyplot.show()
|
Die beiden Scatter-Plots zeigen, das Häuser (blau) in allen Dimensionen die größte Varianz haben. Büros (gelb) können größer und höher ausfallen, als Wohnungen (rot), haben dafür jedoch tendenziell ein kleineres IA_Ratio. Könnten die Kategorien (blau, gelb, rot) durch das Verhältnis innerhalb von einem der beiden Dimensionspaaren in dem zwei dimensionalen Raum exakt voneinander abgegrenzt werden, könnten wir hier stoppen und bräuchten auch keinen kNN-Algorithmus mehr. Da wir jedoch einen großen Überschneidungsbereich in beiden Dimensionspaaren haben (und auch Wandfläche zu IA_Ratio sieht nicht besser aus),
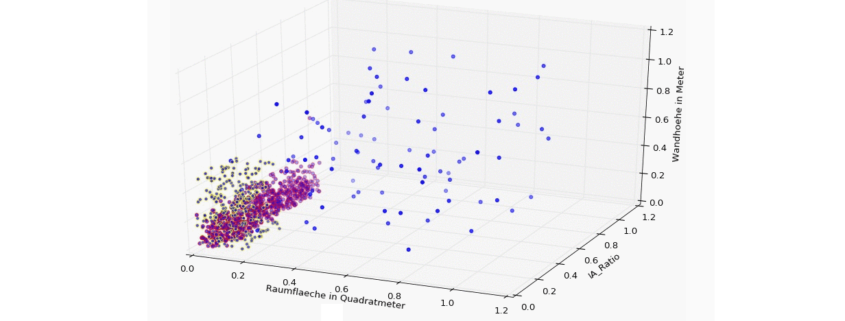
Eine 3D-Visualisierung eignet sich besonders gut, einen Überblick über die Verhältnisse zwischen den drei Metriken zu erhalten: (die Werte wurden hier bereits normalisiert, liegen also zwischen 0,00 und 1,00)
![3D Scatter Plot in Python [Matplotlib]](https://data-science-blog.com/de/wp-content/uploads/sites/5/2016/04/3d-scatter-plot-immobilien-klassifikation-gap.jpg) |
fig = pyplot.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(dataSet[:,0], dataSet[:,2], dataSet[:,1], marker='o', color=classColorVector)
ax.set_xlabel("Raumflaeche in Quadratmeter")
ax.set_ylabel("IA_Ratio")
ax.set_zlabel("Wandhoehe in Meter")
ax.set_xlim(xmin=0)
ax.set_ylim(ymin=0)
ax.set_zlim(zmin=0)
pyplot.show()
|
Es zeigt sich gerade in der 3D-Ansicht recht deutlich, dass sich Büros und Wohnungen zum nicht unwesentlichen Teil überschneiden und hier jeder Algorithmus mit der Klassifikation in Probleme geraten wird, wenn uns wirklich nur diese drei Dimensionen zur Verfügung stehen.
Schritt 3 – Kalkulation der Distanzen zwischen den einzelnen Punkten
Bei der Berechnung der Distanz in einem Raum hilft uns der Satz des Pythagoras weiter. Die zu überbrückende Distanz, um von A nach B zu gelangen, lässt sich einfach berechnen, wenn man entlang der Raumdimensionen Katheten aufspannt.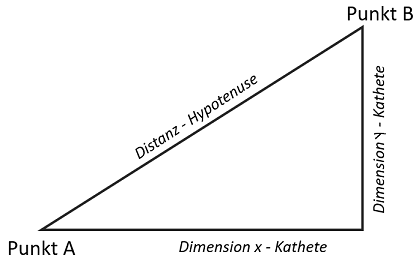
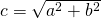
Die Hypotenuse im Raum stellt die Distanz dar und berechnet sich aus der Wurzel aus der Summe der beiden Katheten im Quadrat. Die beiden Katheten bilden sich aus der Differenz der Punktwerte (q, p) in ihrer jeweiligen Dimension.Bei mehreren Dimensionen gilt der Satz entsprechend:
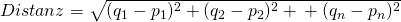
Um mit den unterschiedlichen Werte besser in ihrer Relation zu sehen, sollten sie einer Normalisierung unterzogen werden. Dabei werden alle Werte einer Dimension einem Bereich zwischen 0.00 und 1.00 zugeordnet, wobei 0.00 stets das Minimum und 1.00 das Maximum darstellt.
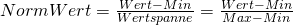
$
def normalizeDataSet(dataSet):
dataSet_n = numpy.zeros(numpy.shape(dataSet)) #[[ 0. 0. 0.]
# [ 0. 0. 0.]
# [ 0. 0. 0.]
# ...,
# [ 0. 0. 0.]
# [ 0. 0. 0.]
# [ 0. 0. 0.]]
minValues = dataSet.min(0) # [ 10. 2.6 0.]
ranges = dataSet.max(0) - dataSet.min(0) # [ 1775. 2.4 68.]
minValues = dataSet.min(0) # [ 10. 2.6 0.]
maxValues = dataSet.max(0) # [ 1785. 5. 68.]
ranges = maxValues - minValues # [ 1775. 2.4 68.]
rowCount = dataSet.shape[0] # 1039
# numpy.tile() wiederholt Sequenzen (hier: [[ 10. 2.6 0. ], ..., [ 10. 2.6 0. ]]
dataSet_n = dataSet - numpy.tile(minValues, (rowCount, 1)) #[[ 2.56000000e+02 9.00000000e-01 1.80000000e+01]
# [ 6.60000000e+01 2.00000000e-01 5.40000000e+01]
# [ 3.32000000e+02 1.50000000e-01 1.00000000e+01]
# ...,
# [ 1.58000000e+02 6.00000000e-01 0.00000000e+00]
# [ 5.70000000e+01 1.00000000e-01 5.20000000e+01]
# [ 1.68000000e+02 2.00000000e-01 0.00000000e+00]]
dataSet_n = dataSet_n / numpy.tile(ranges, (rowCount, 1)) #[[ 0.14422535 0.375 0.26470588]
# [ 0.0371831 0.08333333 0.79411765]
# [ 0.18704225 0.0625 0.14705882]
# ...,
# [ 0.08901408 0.25 0.]
# [ 0.03211268 0.04166667 0.76470588]
# [ 0.09464789 0.08333333 0.]]
#print(dataSet_n)
return dataSet_n, ranges, minValues
Die Funktion kann folgendermaßen aufgerufen werden:
dataSet_n, ranges, minValues = normalizeDataSet(dataSet)
Schritt 4 & 5 – Klassifikation durch Eingrenzung auf k-nächste Nachbarn
Die Klassifikation erfolgt durch die Kalkulation entsprechend der zuvor beschriebenen Formel für die Distanzen in einem mehrdimensionalen Raum, durch Eingrenzung über die Anzahl an k Nachbarn und Sortierung über die berechneten Distanzen.
def classify(inX, dataSet, labels, k):
rowCount = dataSet.shape[0] # Anzahl an Zeilen bestimmen
diffMat = numpy.tile(inX, (rowCount,1)) - dataSet # Berechnung der Katheten
# (über tile() wird der Eingangsdatensatz über die Zeilenanzahl des dataSet vervielfacht,
# der dataSet davon substrahiert)
sqDiffMat = diffMat**2 # Quadrat der Katheten
sqDistances = sqDiffMat.sum(axis=1) # Aufsummieren der Differenzpaare
distances = sqDistances**0.5 # Quadratwurzel über alle Werte
sortedDistIndicies = distances.argsort() # Aufsteigende Sortierung
classCount = {}
#print("inX = %s, k = %s" % (inX, k))
#print(sortedDistIndicies)
for i in range(k): # Eingrenzung auf k-Werte in der sortierten Liste
closest = labels[sortedDistIndicies[i]] # Label (Kategorie [Büro, Wohnung, Haus] entsprechend der Sortierung aufnehmen
classCount[closest] = classCount.get(closest, 0) + 1 # Aufbau eines Dictionary über die
sortedClassCount = sorted(classCount, key = classCount.get, reverse=True) # Absteigende Sortierung der gesammelten Labels in k-Reichweite
# wobei die Sortierung über den Count (Value) erfolgt
#print(classCount)
#print(sortedClassCount[0])
return sortedClassCount[0] # Liefere das erste Label zurück
# also das Label mit der höchsten Anzahl innerhalb der k-Reichweite
Über folgenden Code rufen wir die Klassifikations-Funktion auf und legen die k-Eingrenzung fest, nebenbei werden Fehler gezählt und ausgewertet. Hier werden der Reihe nach die ersten 30 Zeilen verarbeitet:
errorCount = 0
k = 5 # k-Eingrenzung (hier: auf 5 Nachbarn einschränken)
rowCount = dataSet_n.shape[0] # Anzahl der Zeilen im gesamten Datensatz
numTestVectors = 30 # Datensätze 0 - 29 werden zum testen von k verwendet,
# die Datensätze ab Zeile 30 werden zur Klassifikation verwendet
for i in range(0, numTestVectors): # Aufruf des Klassifikators von 0 bis 29
result = classify(dataSet_n[i,:], dataSet_n[numTestVectors:rowCount,:], classLabelVector[numTestVectors:rowCount], k)
print("%s - the classifier came back with: %s, the real answer is: %s" %(i, result, classLabelVector[i]))
if (result != classLabelVector[i]):
errorCount += 1.0
print("Error Count: %d" % errorCount)
Nur 30 Testdatensätze auszuwählen ist eigentlich viel zu knapp bemessen und hier nur der Übersichtlichkeit geschuldet. Besser ist für dieses Beispiel die Auswahl von 100 bis 300 Datensätzen. Die Ergebnisse sind aber bereits recht ordentlich, allerdings fällt dem Algorithmus – wie erwartet – noch die Unterscheidung zwischen Wohnungen und Büros recht schwer.
0 – klassifiziert wurde: Buero, richtige Antwort: Buero
1 – klassifiziert wurde: Wohnung, richtige Antwort: Wohnung
2 – klassifiziert wurde: Buero, richtige Antwort: Buero
3 – klassifiziert wurde: Buero, richtige Antwort: Buero
4 – klassifiziert wurde: Wohnung, richtige Antwort: Wohnung
5 – klassifiziert wurde: Wohnung, richtige Antwort: Wohnung
6 – klassifiziert wurde: Wohnung, richtige Antwort: Wohnung
7 – klassifiziert wurde: Wohnung, richtige Antwort: Buero
8 – klassifiziert wurde: Wohnung, richtige Antwort: Wohnung
9 – klassifiziert wurde: Wohnung, richtige Antwort: Wohnung
10 – klassifiziert wurde: Wohnung, richtige Antwort: Wohnung
11 – klassifiziert wurde: Wohnung, richtige Antwort: Wohnung
12 – klassifiziert wurde: Buero, richtige Antwort: Buero
13 – klassifiziert wurde: Wohnung, richtige Antwort: Buero
14 – klassifiziert wurde: Wohnung, richtige Antwort: Wohnung
15 – klassifiziert wurde: Wohnung, richtige Antwort: Wohnung
16 – klassifiziert wurde: Buero, richtige Antwort: Buero
17 – klassifiziert wurde: Wohnung, richtige Antwort: Wohnung
18 – klassifiziert wurde: Haus, richtige Antwort: Haus
19 – klassifiziert wurde: Wohnung, richtige Antwort: Wohnung
20 – klassifiziert wurde: Wohnung, richtige Antwort: Wohnung
21 – klassifiziert wurde: Buero, richtige Antwort: Buero
22 – klassifiziert wurde: Buero, richtige Antwort: Buero
23 – klassifiziert wurde: Buero, richtige Antwort: Buero
24 – klassifiziert wurde: Wohnung, richtige Antwort: Wohnung
25 – klassifiziert wurde: Wohnung, richtige Antwort: Wohnung
26 – klassifiziert wurde: Wohnung, richtige Antwort: Wohnung
27 – klassifiziert wurde: Wohnung, richtige Antwort: Wohnung
28 – klassifiziert wurde: Wohnung, richtige Antwort: Wohnung
29 – klassifiziert wurde: Buero, richtige Antwort: Buero
Error Count: 2
Über weitere Tests wird deutlich, dass k nicht zu niedrig und auch nicht zu hoch gesetzt werden darf.
| Datensätze |
k |
Fehler |
| 150 |
1 |
25 |
| 150 |
3 |
23 |
| 150 |
5 |
21 |
| 150 |
20 |
26 |
Ein nächster Schritt wäre die Entwicklung eines Trainingprogramms, dass die optimale Konfiguration (k-Eingrenzung, Gewichtung usw.) ermittelt.
Fehlerraten herabsenken
Die Fehlerquote ist im Grunde niemals ganz auf Null herabsenkbar, sonst haben wir kein maschinelles Lernen mehr, sondern könnten auch feste Regeln ausmachen, die wir nur noch einprogrammieren (hard-coding) müssten. Wer lernt, macht auch Fehler! Dennoch ist eine Fehlerquote von 10% einfach zu viel für die meisten Anwendungsfälle. Was kann man hier tun?
- Den Algorithmus verbessern (z. B. optimale k-Konfiguration und Gewichtung finden)
- mehr Merkmale finden (= mehr Dimensionen)
- mehr Daten hinzuziehen (gut möglich, dass alleine dadurch z. B. Wohnungen und Büros besser unterscheidbar werden)
- einen anderen Algorithmus probieren (kNN ist längst nicht für alle Anwendungen ideal!)
Das Problem mit den Dimensionen
Theoretisch kann kNN mit undenklich vielen Dimensionen arbeiten, allerdings steigt der Rechenaufwand damit auch ins unermessliche. Der k-nächste-Nachbar-Algorithmus ist auf viele Daten und Dimensionen angewendet recht rechenintensiv.
In der Praxis hat nicht jedes Merkmal die gleiche Tragweite in ihrer Bedeutung für die Klassifikation und mit jeder weiteren Dimension steigt auch die Fehleranfälligkeit, insbesondere durch Datenfehler (Rauschen). Dies kann man sich bei wenigen Dimensionen noch leicht bildlich vorstellen, denn beispielsweise könnten zwei Punkte in zwei Dimensionen nahe beieinander liegen, in der dritten Dimension jedoch weit auseinander, was im Ergebnis dann eine lange Distanz verursacht. Wenn wir beispielsweise 101 Dimensionen berücksichtigen, könnten auch hier zwei Punkte in 100 Dimensionen eng beieinander liegen, läge jedoch in der 101. Dimension (vielleicht auch auf Grund eines Datenfehlers) eine lange Distanz vor, wäre die Gesamtdistanz groß. Mit Gewichtungen könnten jedoch als wichtiger einzustufenden Dimensionen bevorzugt werden und als unsicher geltende Dimensionen entsprechend entschärft werden.
Je mehr Dimensionen berücksichtigt werden sollen, desto mehr Raum steht zur Verfügung, so dass um wenige Datenpunkte viel Leerraum existiert, der dem Algorithmus nicht weiterhilft. Je mehr Dimensionen berücksichtigt werden, desto mehr Daten müssen zu Verfügung gestellt werden, im exponentiellen Anstieg – Wo wir wieder beim Thema Rechenleistung sind, die ebenfalls exponentiell ansteigen muss.
Weiterführende Literatur


Machine Learning in Action

Introduction to Machine Learning with Python

Einführung in Data Science: Grundprinzipien der Datenanalyse mit Python







![3D Scatter Plot in Python [Matplotlib]](https://data-science-blog.com/de/wp-content/uploads/sites/5/2016/04/3d-scatter-plot-immobilien-klassifikation-gap.jpg)