Was der BREXIT für die Cloud-Strategie bedeutet
Datensouveränität wird nach dem Brexit eine der größten Herausforderungen für Unternehmen sein. Geschäftsführer sind sich der Bedeutung dessen bewusst und fürchten die Gefahr eines „Data cliff edge“, wenn die Trennung Großbritanniens von der EU endgültig beschlossene Sache sein wird.
Ohne ein klares Gespür dafür zu haben, welche Vorschriften und Compliance-Anforderungen bald gelten werden, versuchen britische Unternehmen herauszufinden, wie sie ihre Daten bestmöglich schützen, Geschäftsverzögerungen verhindern und kostspielige Fehler vermeiden können. Die Vieldeutigkeit rund um den Brexit wirft mehr Fragen als Antworten auf, darunter: Wo sollten britische Unternehmen ihre Daten speichern? Sollten sie alle ihre Rechenzentren nach Großbritannien verlegen? Wie wirkt sich der Besitz von Rechenzentren auf den Datenschutz aus? Welche Bedrohungen bestehen, wenn nach Abschluss des Brexit Daten innerhalb oder außerhalb des Vereinigten Königreichs gespeichert werden?
Für Führungskräfte sind der Mangel an Antworten und die Angst vor dem Unbekannten frustrierend. In dieser ungewissen Zeit können smarte Geschäftsführer aber den Brexit für ihre Zwecke lenken, indem sie ihn als Chance und nicht als Hindernis für sich nutzen.
Die unsicher regulierte Zukunft
Für Unternehmen mit Sitz in Großbritannien, die Datenspeicherung und private Cloud-Dienste anbieten, ist vor allem der Ort, an dem sich die Daten befinden, von Belang. Die Gewährleistung der Sicherheit und Kontrolle über eigene Daten ist von zentraler Bedeutung. Gleichzeitig ist jedoch auch die Einhaltung unbekannter zukünftiger Vorschriften und Gesetze zum Datenschutz und zum Datentransfer ein Muss.
Grundlage ist die Einhaltung der Datenschutzverordnung (DSGVO) vom 25. Mai 2018, da das Vereinigte Königreich zu diesem Zeitpunkt noch immer Teil der EU war. Nach Angaben des Information Commissioner’s Office (ICO) des Vereinigten Königreichs – einer unabhängigen Behörde, die sich für die Wahrung von Informations- und Datenschutzrechten von Einzelpersonen einsetzt – bestätigte die britische Regierung, dass ein Austritt aus der EU keine Auswirkungen auf die DSGVO haben wird. Was in diesem Jahr, wenn sich Großbritannien und die EU endgültig voneinander trennen, passieren wird, kann man nur vermuten. Die Ratschläge von ICO sind richtungsweisend: „Bereiten Sie sich darauf vor, die Bestimmungen der DSGVO zu erfüllen und voranzukommen.“
Bemerkenswerterweise schreibt die DSGVO nicht vor, wo Unternehmen ihre Daten aufbewahren müssen. Es ist lediglich erforderlich, dass die EU-Organisationen ihre Daten innerhalb der EU speichern und außerhalb der EU unzugänglich machen müssen. Ausnahme: die Daten betreffen eine DSGVO-konforme Organisation. Wie sich dieses Mandat auf das Vereinigte Königreich auswirkt, muss noch gesehen werden. Denn das Vereinigte Königreich war ja zum Zeitpunkt der Ausarbeitung der Verordnung Teil der EU. Es ist unklar, ob das Vereinigte Königreich am Ende mit der DSGVO konform sein wird.
Aus globaler Sicht muss Großbritannien herausfinden, wie der Datenaustausch und der grenzüberschreitende Datenfluss reguliert werden können. Der freie Datenfluss ist wichtig für Unternehmen und Innovation, was bedeutet, dass das Vereinigte Königreich Vereinbarungen, wie die EU sie mit den USA getroffen haben, benötigt. Ein Privacy Shield, das den Austausch personenbezogener Daten zu gewerblichen Zwecken ermöglicht. Ob das Vereinigte Königreich Vereinbarungen wie den Privacy Shield umsetzen kann, oder neue Vereinbarungen mit Ländern wie den USA treffen muss, ist etwas, was nur die Zeit zeigen wird.
Wo sind die Daten?
Rechenzentren können heute durch freien Datenfluss, sowohl im Vereinigten Königreich als auch in der EU betrieben werden. Das Vereinigte Königreich unterliegt gleichem Schutz und gleichen Vorschriften wie die EU. Viele Spekulationen beinhalten allerdings, dass in naher Zukunft britische Kunden von einem in Großbritannien ansässigen Rechenzentrum bedient werden müssen, ebenso wie europäische Kunden ein EU-Rechenzentrum benötigen. Es gibt keine Garantien. Unklar ist auch, ob diese Situation die Anbieter von Rechenzentren dazu veranlassen wird, den Umzug aus Großbritannien in Betracht zu ziehen, um sich stärker auf den Kontinent zu konzentrieren, oder ob sie sich an beiden Standorten gleichzeitig niederlassen werden. Das Wahrscheinlichste: Die Anbieter tendieren zu letzterem, wie auch Amazon Web Services (AWS). Selbst nach dem Brexit-Votum hielt Amazon an seinem Wort fest und eröffnete Ende letzten Jahres sein erstes AWS-Rechenzentrum in London. Dies unterstreicht sowohl sein Engagement für Großbritannien als auch das unternehmerische Engagement.
Aus dem Brexit eine Geschäftsmöglichkeit machen
Die Automatisierung des IT-Betriebs und die Einführung einer Cloud-Strategie könnten die ersten Schritte sein, um die unbeantworteten Fragen des Brexit zu lösen und daraus einen Vorteil zu machen. Es ist an der Zeit, die Vorteile dessen zu erkennen, teure Hardware und Software von Unternehmen vor Ort durch den Umstieg auf die öffentliche Cloud zu ersetzen. Dies ist nicht nur die kostengünstigere Option. Cloud-Anbieter wie AWS, Microsoft Azure und Google Cloud Platform (GCP) ersparen in diesem politischen Umfeld sogar Unternehmen die Verwaltung und Wartung von Rechenzentren. Einige Unternehmen sind möglicherweise besorgt über die steigenden Raten von Public-Cloud-Anbietern, ihre Preisanpassungen scheinen jedoch an den relativen Wertverlust des Sterlings gebunden zu sein. Selbst bei geringen Erhöhungen sind die Preise einiger Anbieter, wie AWS, noch immer deutlich niedriger als die Kosten, die mit dem Betrieb von Rechenzentren und privaten Clouds vor Ort verbunden sind, insbesondere wenn Wartungskosten einbezogen werden. Wenn man diesen Gedanken noch einen Schritt weiterführt, wie kann der Brexit als eine Chance für Unternehmen betrachtet werden?Organisationen sammeln alle Arten von Daten. Aber nur eine Handvoll von ihnen verwendet effektive Datenanalysen, die Geschäftsentscheidungen unterstützen. Nur wenige Unternehmen tun mehr, als ihre Daten zu speichern, da ihnen die Tools und Ressourcen fehlen, um nahtlos auf ihre Daten zuzugreifen, oder weil Abfragen teuer sind. Ohne ein für die Cloud konstruiertes Data Warehouse ist dieser Prozess bestenfalls eine Herausforderung, und der wahre Wert der Daten geht dabei verloren. Ironischerweise bietet der Brexit die Möglichkeit, dies zu ändern, da Unternehmen ihre IT-Abläufe neu bewerten und alternative, kostengünstigere Methoden zum Speichern von Daten suchen müssen. Durch den Wechsel zu einer öffentlichen Cloud und die Nutzung eines Data Warehouses für die Cloud können Unternehmen Beschränkungen und Einschränkungen ihrer Daten aufheben und diese für die Entscheidungsfindung zugänglich machen.
Der Brexit dient also als Katalysator einer datengesteuerten Organisation, die Daten verwendet, anstatt sie für schlechte Zeiten zu speichern. Am Ende scheint die Prognose der Verhandlungen in Brüssel doch eine ziemlich stürmische zu sein.





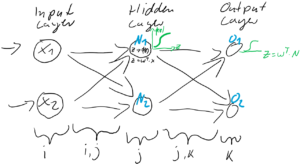
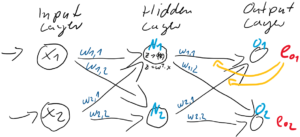
![Rendered by QuickLaTeX.com \[ e_{N} = \left(\begin{array}{rr} \frac{w_{1,1}}{w_{1,1} + w_{1,2}} & \frac{w_{1,2}}{w_{1,1} + w_{1,2}} \\ \frac{w_{2,1}}{w_{2,1} + w_{2,2}} & \frac{w_{2,2}}{w_{2,1} + w_{2,2}} \end{array}\right) \cdot \left(\begin{array}{c} e_{1} \\ e_{2} \end{array}\right) \qquad \]](https://data-science-blog.com/de/wp-content/ql-cache/quicklatex.com-6fadfe69caec8e8c351788824875138a_l3.png)





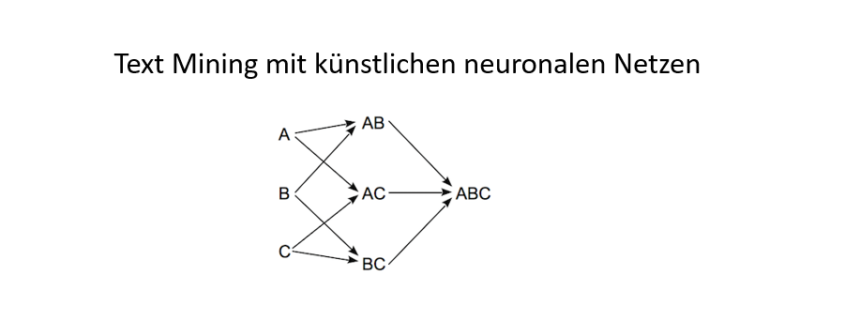
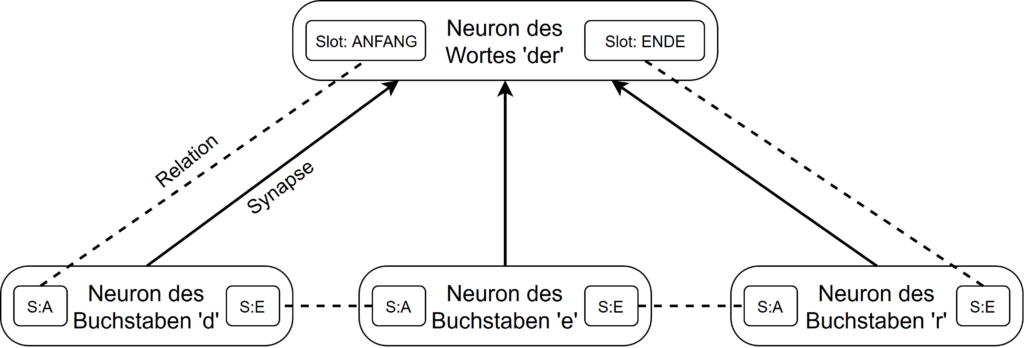
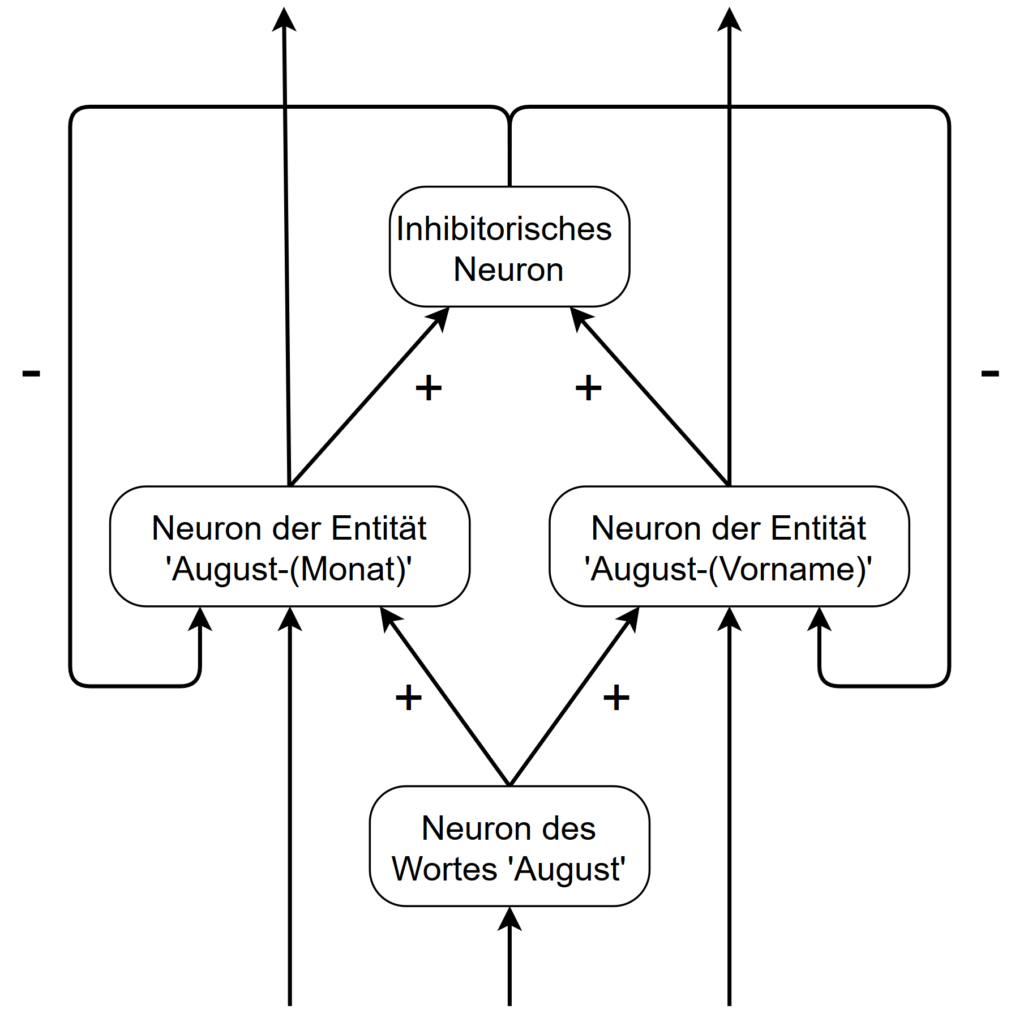



![Rendered by QuickLaTeX.com text)) # Jedes einzigartige Wort und dazugehörige Häufigkeiten. words <- rownames(words) # wfm zählt Häufigkeiten jedes Wortes und schreibt Wörter in rownames, wir brauchen jedoch das Wort selbst. </pre> Danach wird eine leere Liste erstellt, in der iterativ für jedes Element des Suchvektors ein Charactervektor erzeugt wird, der Wörter enthält, die einen Jaro-Winker Score von 0,9 oder höher besitzen. <pre class="theme:github lang:r decode:true ">for(i in 1:length(startliste)) { finalewortliste[[i]] <- words[which(jarowinkler(startliste[[i]], words) > 0.9)] } </pre> Jetzt wird ein leerer DataFrame erzeugt, der die Zeilenlänge des originalen DataFrames besitzt sowie die Anzahl der Marken als Spaltenlänge. <pre class="theme:github lang:r decode:true ">finaldf <- data.frame(matrix(nrow = nrow(df), ncol = length(startliste))) colnames(finaldf) <- startliste </pre> Im nächsten Schritt wird nun aus den ähnlichen Wörtern mit einer oder-Verknüpfung einen String erzeugt, der alle durch den Jaro-Winkler-Score identifizierten Wörter beinhaltet. Wenn ein Treffer gefunden wird, wird in der Suchspalte eine Eins eingetragen, ansonsten eine Null. <pre class="theme:github lang:r decode:true ">for(i in 1:ncol(finaldf)) { finaldf[i] <- ifelse(str_detect(df](https://data-science-blog.com/de/wp-content/ql-cache/quicklatex.com-4c818216532cfcfb704402489fc62a58_l3.png) text, paste(finalewortliste[[i]], collapse = "|")) == TRUE, 1, 0)
}
text, paste(finalewortliste[[i]], collapse = "|")) == TRUE, 1, 0)
}
 text, finaldf)
colnames(finaldf)[1] <- "text"
# Ergebnisse in eine .xlsx Datei schreiben.
wb <- createWorkbook()
addWorksheet(wb, "Ergebnisse")
writeData(wb, "Ergebnisse", anteil, startCol = 2, startRow = 1, rowNames = FALSE)
writeData(wb, "Ergebnisse", finaldf, startCol = 1, startRow = 4, rowNames = FALSE)
saveWorkbook(wb, paste0("C:/Users/User/Desktop/Results_", Sys.Date(), ".xlsx"), overwrite = TRUE)
text, finaldf)
colnames(finaldf)[1] <- "text"
# Ergebnisse in eine .xlsx Datei schreiben.
wb <- createWorkbook()
addWorksheet(wb, "Ergebnisse")
writeData(wb, "Ergebnisse", anteil, startCol = 2, startRow = 1, rowNames = FALSE)
writeData(wb, "Ergebnisse", finaldf, startCol = 1, startRow = 4, rowNames = FALSE)
saveWorkbook(wb, paste0("C:/Users/User/Desktop/Results_", Sys.Date(), ".xlsx"), overwrite = TRUE)
