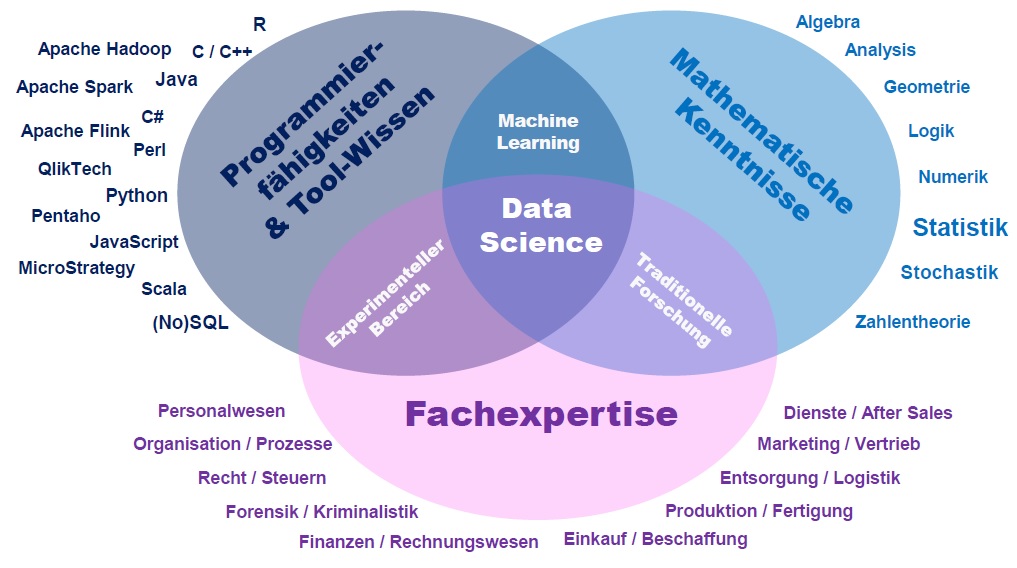
Die ABC-XYZ-Analyse ist eine aussagekräftige Analyse für die Strategiefindung in der Warenwirtschaft und Logistik bzw. im Supply Chain Management. Die Analyse basiert auf der Vorstellung einer Pareto-Verteilung, die darauf hindeutet, dass oftmals eine kleine Menge eines großen Ganzen einen unverhältnismäßig großen Einfluss auf eben dieses große Ganze hat.
Die ABC-XYZ-Analyse beinhaltet im ersten Schritt eine ABC- und im zweiten Schritt eine XYZ-Analyse. Im dritten Schritt werden die Ergebnisse in einer Matrix zusammengeführt. In diesem Artikel erläutere ich nicht, wofür eine ABC-XYZ-Analyse dient und wie die Ergebnisse zu interpretieren sind, hier kann ich jedoch auf einen älteren Artikel “ABC-XYZ-Analyse” – www.der-wirtschaftsingenieur.de vom 3. Mai 2011 von mir verweisen, der vorher lesenswert ist, wenn kein Vorwissen zur ABC-XYZ-Analyse vorhanden ist.
Die Vorarbeit
Für die ABC- und XYZ-Analyse benötigen wir folgende Python-Bibliotheken:
import pandas as pd
import numpy as np
import random as random
import matplotlib.pyplot as pyplot
Wir laden die EKPO-Tabelle in ein DataFrame (Datenstruktur der Pandas-Bibliothek):
EKPO = pd.read_csv("[PFAD]EKPO.csv", delimiter=';', thousands='.', decimal=',')
Die Datei stammt aus einem SAP-Testsystem und steht hier zum Download bereit:

SAP.EKPO
Wir benötigen daraus nur folgende Zeilen:
EKPO_X = EKPO[['MATNR', 'MATKL', 'MENGE', 'PEINH', 'NETPR', 'NETWR']].copy()
Jetzt kommt der erste Kniff: Das Feld “MENGE” im SAP beschreibt die Menge in der jeweiligen Mengeneinheit (z. B. Stück, Meter oder Liter). Da wir hier jedoch nicht den genauen Verbrauch vorliegen haben, sondern nur die Einkaufsmenge (indirekt gemessener Verbrauch), sollten wir die Menge pro Preiseinheit “PEINH” berücksichtigen, denn nach dieser Preiseinheitsmenge erfolgt der Einkauf.
EKPO_X['Preiseinheitsmenge'] = EKPO_X['MENGE'] / EKPO_X['PEINH']
Für die Preiseinheitsmenge ein Beispiel:
Sie kaufen sicherlich pro Einkauf keine 3 Rollen Toilettenpapier, sondern eine oder mehrere Packungen Toilettenpapier. Wenn Sie zwei Packung Toilettenpapier für jeweils 2 Euro kaufen, die jeweils 10 Rollen beinhalten, ist die Preiseinheit = 10 und die Preiseinheitsmenge => 20 gekaufte Toilettenrollen / 10 Rollen pro Packung = 2 Packungen Toilettenpapier.
Nun haben wir also unsere für den Einkauf relevante Mengeneinheit. Jetzt sortieren wir diese Materialeinkäufe primär nach dem Umsatzvolumen “NETWR” absteigend (und sekundär nach der Preiseinheitsmenge aufsteigend, allerdings spielt das keine große Rolle):
EKPO_X = EKPO_X.sort_values(by = ['NETWR', 'Preiseinheitsmenge'], ascending=[False, True]) # Sortierung nach Umsatzvolumen pro Bestellung absteigend
Einige Störfaktoren müssen noch bereinigt werden. Erstens sollen Einträge mit Preisen oder Umsätzen in Höhe von 0,00 Euro nicht mehr auftauchen:
EKPO_X = EKPO_X[(EKPO_X.NETPR != 0) & (EKPO_X.NETWR != 0)]
Zweitens gibt es Einkäufe, die ein Material ohne Materialnummer und/oder ohne Materialklasse haben. Bei einer Zusammenfassung (Aggregation) über die Materialnummer oder die Materialklasse würden sich diese “leeren” Einträge als NULL-Eintrag bündeln. Das wollen wir vermeiden, indem wir alle NULL-Einträge mit jeweils unterschiedlichen Zufallszahlen auffüllen.
EKPO_X.MATNR[EKPO_X.MATNR.isnull() == True] = EKPO_X.MATNR[EKPO_X.MATNR.isnull() == True].apply(lambda x: random.random()) # Manche MATNR fehlen (NULL), diese füllen wir mit zufälligen Werten auf. Dabei ist es natürlich wichtig, dass die Zufallszahl für jede Zeile neu generiert wird! EKPO_X.MATNR.fillna(random.random()) funktioniert nicht, denn hier würde ein gleicher Wert alle NaN-Werte ersetzen
ABC – Analyse:
Nun geht es an die eigentliche ABC-Analyse, dafür müssen wir die Gruppierung der Materialien vornehmen. Gleich vorweg: Dies sollte man eigentlich über die einzelnen Materialnummern machen, da dies jedoch in der Visualisierung (auf Grund der hohen Anzahl und Vielfältigkeit) etwas aufwändiger ist, machen wir es über die Materialklassen. Wir gehen dabei einfach davon aus, dass die Materialklassen relativ homogene Materialien zusammenfassen und somit auch das Verbrauchs-/Einkaufverhalten innerhalb einer Gruppe nicht sonderlich viel Abweichung aufweist.
Materialklasse
# Aggregation über die Materialklasse, Aufsummierung der Umsätze, Mengen und Volumen
MATKL_MENGEN = (EKPO_X.MENGE.groupby(EKPO_X.MATKL).sum()).to_frame()
MATKL_PREISEINHEIT_MENGE = (EKPO_X.Preiseinheitsmenge.groupby(EKPO_X.MATKL).sum()).to_frame()
MATKL_VOLUMEN = (EKPO_X.NETWR.groupby(EKPO_X.MATKL).sum()).to_frame()
# Aggregation über die Materialklasse, Berechnung des Durchschnittpreises (ist bei einer Materialklasse, allerdings wenig sinnvoll!)
MATKL_Preise = (EKPO_X.NETPR.groupby(EKPO_X.MATKL).mean()).to_frame()EKPO_G = MATKL_MENGEN.join(MATKL_PREISEINHEIT_MENGE, how='left')
# Zusammenfügen der Ergebnisse (Left-Join)
EKPO_G = EKPO_G.join(MATKL_Preise, how='left')
EKPO_G = EKPO_G.join(MATKL_VOLUMEN, how='left')
EKPO_G = EKPO_G.sort_values(['NETWR'], ascending=False)
# Berechnung der kumulierten Umsätze und Mengen (Beachte: Vorher muss nach Umsätzen absteigend sortiert worden sein! (siehe oben)
EKPO_G['Volumen_kumuliert'] = EKPO_G.NETWR.cumsum()
EKPO_G['Menge_kumuliert'] = EKPO_G.MENGE.cumsum()
Materialnummer
MATNR_MENGEN = EKPO_X.MENGE.groupby(EKPO_X.MATNR).sum()
MATNR_PREISEINHEIT_MENGE = EKPO_X.Preiseinheitsmenge.groupby(EKPO_X.MATNR).sum()
MATNR_VOLUMEN = EKPO_X.NETWR.groupby(EKPO_X.MATNR).sum()
MATNR_Preise = EKPO_X.NETPR.groupby(EKPO_X.MATNR).mean()MATNR_MENGEN = MATNR_MENGEN.to_frame()
MATNR_PREISEINHEIT_MENGE = MATNR_PREISEINHEIT_MENGE.to_frame()
MATNR_Preise = MATNR_Preise.to_frame()
MATNR_VOLUMEN = MATNR_VOLUMEN.to_frame()EKPO_G = MATNR_MENGEN.join(MATNR_PREISEINHEIT_MENGE, how='left')
EKPO_G = EKPO_G.join(MATNR_Preise, how='left')
EKPO_G = EKPO_G.join(MATNR_VOLUMEN, how='left')
EKPO_G = EKPO_G.sort_values(['NETWR'], ascending=False)
EKPO_G['Volumen_kumuliert'] = EKPO_G.NETWR.cumsum()
EKPO_G['Menge_kumuliert'] = EKPO_G.MENGE.cumsum()
Nun können wir uns ganz im Sinne der ABC-Analyse die typische Pareto-Verteilung der kumulierten Umsätze (Umsatzgrößen absteigend sortiert) ansehen:
EKPO_G[['Menge_kumuliert','Volumen_kumuliert']].plot([EKPO_G.Menge_kumuliert, EKPO_G.Volumen_kumuliert], color=['red','pink'], figsize=[20,10], fontsize=8, title='Kumulierte Werte - Sortierung nach Materialklassen-Volumen')

Die X-Achse zeigt die Materialklassen von links nach rechts in der Sortierung nach dem Umsatzvolumen (größester Umsatz links, kleinster Umsatz rechts). Die Y-Achse zeigt den Betrag der Umsatzhöhe (Euro) bzw. der Menge (Preiseinheitsmenge). Die Kurve der Menge ist mit Vorsicht zu bewerten, da primär nach dem Umsatz und nicht nach der Menge sortiert wurde.
Klassifikation:
Nun kommen wir zur Klassifikation. Hier machen wir es uns sehr einfach: Wir gehen einfach davon aus, dass 80% des Wertbeitrages aller Umsätze von etwa 20% der Materialien (hier: Materialklassen) umfassen und klassifizieren daher über feste relative Größen:
EKPO_G['ABC_Gruppe'] = "C" # Erstmal sind alle Materialien der C-Gruppe zugeordnet
EKPO_G['ABC_Gruppe'][EKPO_G.Volumen_kumuliert <= EKPO_G.NETWR.sum() / 100 * 95] = 'B' # Materialien, deren kumuliertes Volumen maximal 95% des Gesamtvolumens umfassen, sind Gruppe B
EKPO_G['ABC_Gruppe'][EKPO_G.Volumen_kumuliert <= EKPO_G.NETWR.sum() / 100 * 80] = 'A' # Materialien, deren kumuliertes Volumen maximal 80% des Gesamtvolumens umfassen, sind Gruppe A
Hinweis:
Intelligenter wird so eine Klassifikation, wenn wir den steilsten Anstieg innerhalb der kumulierten Volumen (die zuvor gezeigte Kurve) ermitteln und danach die Grenzen für die A-, B-, C-Klassen festlegen.
Optional: Farben für die Klassen festlegen (für die nachfolgende Visualisierung)
EKPO_G['Color'] = 'red'
EKPO_G['Color'][EKPO_G['ABC_Gruppe'] == 'B'] = 'orange'
EKPO_G['Color'][EKPO_G['ABC_Gruppe'] == 'C'] = 'green'
Jetzt Aggregieren wir über die ABC-Gruppe:
GruppenWerte = EKPO_G.groupby(['ABC_Gruppe'])
GruppenVolumen = (GruppenWerte.NETWR.sum()).to_frame()
GruppenMengen = (GruppenWerte.Preiseinheitsmenge.sum()).to_frame()
# Wieder zusammenfügen
GruppenVolumenMengen = GruppenVolumen.join(GruppenMengen)
Das Ergebnis:
GruppenVolumenMengen
Out:
NETWR Preiseinheitsmenge
ABC_Gruppe
A 6190725.01 175748.29
B 1231070.86 199599.24
C 408128.45 99745.63
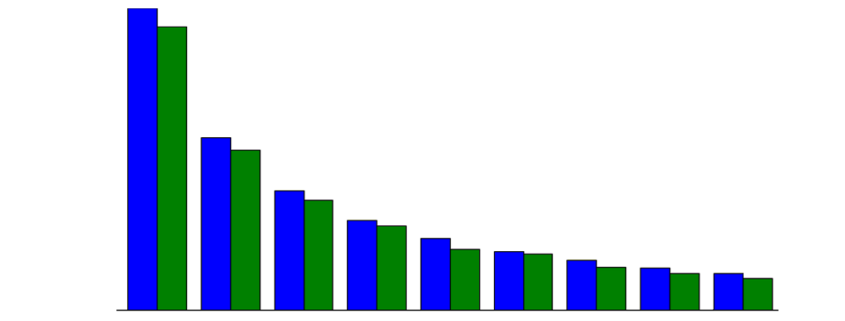
Schauen wir uns nun die Verteilung der Werte und Mengen zwischen den Klassen A, B und C an:
GruppenVolumenMengen.plot(kind='bar', width=0.90, xlim=[0,1000], figsize=[10,5], yticks=GruppenVolumenMengen.NETWR)

Es ist recht gut erkennbar, dass die Gruppe A deutlich mehr Umsatzvolumen (also Wertbeitrag) als die Gruppen B und C hat. Allerdings hat sie auch eine höhere Bestellmenge, wie jedoch nicht proportional von C über B zu A ansteigt wie das Umsatzvolumen.
Nachfolgend sehen wir die Klassifikation nochmal nicht kumuliert über die Umsatzvolumen der Materialien (Materialklassen):
EKPO_G[['NETWR']].plot(kind='bar', figsize=[20,10], legend = True, color=EKPO_G.Color, alpha=0.65, title='ABC - Analyse')

XYZ – Analyse
Für die XYZ-Analyse berechnen wir den arithmetischen Mittelwert, die Standardabweichung und die Summe aller Mengen pro Materialklasse [‘MATKL’] (oder alternativ, der einzelnen Materialnummern [‘MATNR’]) über eine Aggregation:
Material_Menge = EKPO_X.Preiseinheitsmenge.groupby(EKPO_X.MATKL).agg({'mean', 'std', 'sum'})
#Oder mit dem Material: Material_Menge = EKPO_X.Preiseinheitsmenge.groupby(EKPO_X.MATNR) .agg({'mean', 'std', 'sum'})
#Leider ergeben sich einige NaNs bei der Standardabweichung, da ein Material oder eine Materialklasse nur eine einzige Buchung haben kann, diese müssen wir bereinigen (hier: mit Nullen auffüllen):
Material_Menge = Material_Menge.fillna(0)
Die XYZ-Analyse soll aufzeigen, welche Materialien (hier: Materialklassen) in stabilen Mengen verbraucht (hier: eingekauft) werden und welche größere Schwankungen hinsichtlich der Verbrauchsmenge (hier: Einkaufsmenge) aufweisen. Dazu berechnen wir den Variationskoeffizienten:
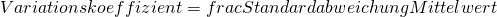
Wir berechnen diesen Variationskoeffizienten und sortieren das DataFrame nach diesem aufsteigend:
Material_Menge['Variationskoeffizient'] = Material_Menge['std'] / Material_Menge['mean']
Material_Menge = Material_Menge.sort_values(['Variationskoeffizient'], ascending = True)
Klassifikation:
Nun klassifizieren wir die Materialien (Materialklassen) über den Variationskoeffizienten in XYZ-Klassen. Dabei gehen wir davon aus, dass Materialien/Materialklassen, die einen Variationskoeffizienten von bis zu 70% des Maximalwertes aufweisen, in die Y-Klasse fallen. Solche, die nur maximal 20% des Maximalwertes aufweisen, fallen in die X-Klasse:
Material_Menge['XYZ_Gruppe'] = 'Z'
Material_Menge['XYZ_Gruppe'][Material_Menge.Variationskoeffizient <= Material_Menge.Variationskoeffizient.max() / 100 * 70] = 'Y'
Material_Menge['XYZ_Gruppe'][Material_Menge.Variationskoeffizient <= Material_Menge.Variationskoeffizient.max() / 100 * 20] = 'X'
Auch hier gilt analog zur ABC-Analyse: Intelligente Klassifikation erfolgt über die Analyse der Kurve der kumulierten Variationskoeffizienten. Die Grenzen der Klassen sollten idealerweise zwischen den steilsten Anstiegen (bzw. die größten Wertedifferenzen) zwischen den Werten der kumulierten Variationskoeffizienten-Liste gezogen werden.
Optional: Farben fürs Plotten setzen.
Material_Menge['Color'] = 'red'
Material_Menge['Color'][Material_Menge.XYZ_Gruppe == 'Y'] = 'orange'
Material_Menge['Color'][Material_Menge.XYZ_Gruppe == 'X'] = 'green'
Jetzt schauen wir uns mal die Verteilung der Materialien hinsichtlich des Variationskoeffizienten an:
Material_Menge.Variationskoeffizient.plot(kind='bar', width=0.90, xlim=[0,1000], figsize=[20,5], rot=90, color=Material_Menge.Color, title='XYZ - Analyse')

Die meisten Materialklassen haben einen recht niedrigen Variationskoeffizienten, sind im Einkauf (und daher vermutlich auch im Verbrauch) recht stabil. Die Materialklasse 0004 hingegen ist einigen Mengenschwankungen unterworfen. In der ABC-Analyse ist diese Materialklasse 0004 als B-Gruppe klassifiziert.
ABC-XYZ-Analyse
Nun möchten wir also die zuvor erstellte ABC-Klassifikation mit der XYZ-Klassifikation zusammen bringen.
Dafür fügen wir die beiden Pandas.DataFrame über den Index (hier die Materialklasse ‘MATKL’, im anderen Fall das Material ‘MATNR’) zusammen:
XYZ_ABC = pd.merge(EKPO_G, Material_Menge, left_index = True, right_index = True, how='left')
Die Zusammenfassung als Kreuztabelle:
pd.crosstab(XYZ_ABC.ABC_Gruppe, XYZ_ABC.XYZ_Gruppe, margins=True)
Out:
X Y Z All
A 17 1 0 18
B 19 1 1 21
C 69 2 0 71
All 105 4 1 110
Für die Interpretation dieser Ergebnisse verweise ich erneut auf den Artikel bei der-wirtschaftsingenieur.de.


 Frau Dr. Eva-Marie Müller-Stüler ist Associate Director in Decision Science der KPMG LLP in London. Sie absolvierte zur Diplom-Mathematikerin an der Technischen Universität München, mit einem einjährigen Auslandssemester in Tokyo, und promovierte an der Philipp Universität in Marburg.
Frau Dr. Eva-Marie Müller-Stüler ist Associate Director in Decision Science der KPMG LLP in London. Sie absolvierte zur Diplom-Mathematikerin an der Technischen Universität München, mit einem einjährigen Auslandssemester in Tokyo, und promovierte an der Philipp Universität in Marburg.