Dr. Dietrich Wettschereck

Toolkits & Services für Semantische Textanalysen

/in , , , , , , , , , /by

Named Entity Recognition ist ein Teilgebiet von Information Extraction. Ziel von Information Extraction ist die Gewinnung semantischer Informationen aus Texten (im Gegensatz zum verwandten Gebiet des Information Retrieval, bei dem es um das möglichst intelligente Finden von Informationen, die u.U. vorab mit Information Extraction gewonnen wurden, geht). Named Entity Recognition (kurz NER) bezeichnet die Erkennung von Entitäten wie z.B. Personen, Organisationen oder Orten in Texten.

[box]Beispiel:
“Albert Einstein war ein theoretischer Physiker, der am 14. März 1879 in Ulm geboren wurde. Er erhielt 1921 den Nobelpreis für Physik. Isaac Newton, Einstein und Stephen Hawking werden oft als die größten Physiker seit der Antike bezeichnet.”[/box]

Die Disambiguierung von Entitäten ist ein weiterer wichtiger Schritt auf dem Weg zu einem semantischen Verständnis von Texten. Wenn man so in obigem Text erkennen kann, dass “Albert Einstein“, “Er” und “Einstein” die gleiche Person bezeichnen, so kann ein Analyseverfahren z.B. daraus schließen, dass in diesem Text Einstein eine wichtigere Rolle spielt, als Newton, der nur einmal erwähnt wurde. Die Hyperlinks hinter den jeweiligen Entitäten zeigen eine Möglichkeit der semantischen Anreicherung von Texten an – in diesem Fall wurden die Entitäten mit entsprechenden Einträgen bei DBpedia automatisch verlinkt.

Named Entity Recognition dient vorrangig zwei Zwecken:

  • Anreicherung von Texten mit Metadaten
  • Abstraktion von Texten zur besseren Erkennung von Mustern

Punkt 1 dient direkt dem Information Retrieval. Anwender können so z.B. gezielt nach bestimmten Personen suchen, ohne alle möglichen Schreibweisen oder Berufsbezeichnungen auflisten zu müssen.

Punkt 2 dient der Vorverarbeitung von Texten als Input für Machine Learning Verfahren. So ist es (je nach Anwendung!) oft nicht von Bedeutung, welche Person, welcher Ort oder auch welche Uhrzeit in einem Text steht sondern nur die Tatsache, dass Personen, Orte oder Zeiten erwähnt wurden.

Sirrus Shakeri veranschaulicht die zentrale Bedeutung semantischer Analyse in seinem Beitrag From Big Data to Intelligent Applications:

intelligent-applications-cirrus-shakeri

Abbildung 1: Von Big Data zu Intelligent Applications von Cirrus Shakeri

Sein “Semantic Graph” setzt voraus, dass Entitäten mittels “Natural Language Processing” erkannt und zueinander in Beziehung gesetzt wurden.

Es ist interessant zu vermerken, dass Natural Language Processing und Data Mining / Machine Learning über viele Jahre als Alternativen zueinander und nicht als Ergänzungen voneinander gesehen wurden. In der Tat springen die meisten Vorgehensmodelle heutzutage von “Data Preparation” zu “Machine Reasoning”. Wir argumentieren, dass sich in vielen Anwendungen, die auf unstrukturierten Daten basieren, signifikante Qualitätsverbesserungen erzielen lassen, wenn man zumindest NER (inklusive Disambiguierung) in die Pipeline mit einbezieht.

Toolkits und Services für NER

Es existiert eine Vielzahl von Toolkits für Natural Language Processing, die Sie mehr oder weniger direkt in Ihre Programme einbinden können. Exemplarisch seien drei Toolkits für Java, Python und R erwähnt:

Diese Toolkits enthalten Modelle, die auf Korpora für die jeweils unterstützten Sprachen trainiert wurden. Sie haben den Vorteil, dass sie auch vollkommen neue Entitäten erkennen können (wie z.B. neue Politiker oder Fernsehstars, die zur Trainingszeit noch unbekannt waren). Je nach Einstellung haben diese Systeme aber auch eine relativ hohe Falsch-Positiv-Rate.

Wer NER nur ausprobieren möchte oder lediglich gelegentlich kleinere Texte zu annotieren hat, sei auf die folgenden Web Services verwiesen, die auch jeweils eine REST-Schnittstelle anbieten.

DBpedia

Das DBpedia Projekt nutzt die strukturierten Informationen der verschieden-sprachigen Wikipedia Sites für den Spotlight Service. Im Unterschied zu den reinen Toolkits nutzen die nun genannten Werkzeuge zusätzlich zu den trainierten Modellen eine Wissensbasis zur Verringerung der Falsch-Positiv-Rate. Die mehrsprachige Version unter http://dbpedia-spotlight.github.io/demo zeigt die Möglichkeiten des Systems auf. Wählen Sie unter “Language” “German“) und dann über “SELECT TYPES…” die zu annotierenden Entitätstypen. Ein Beispieltext wird automatisch eingefügt. Sie können ihn natürlich durch beliebige andere Texte ersetzen. Im folgenden Beispiel wurden “Organisation”, “Person”, und “Place“ ausgewählt:

DBprediaSpotlight

Abbildung 2: DBpedia Demo (de.dbpedia.org)

Die erkannten Entitäten werden direkt mit ihren DBpedia Datenbankeinträgen verlinkt. Im Beispiel wurden die Orte Berlin, Brandenburg und Preußen sowie die Organisationen Deutsches Reich, Deutsche Demokratische Republik, Deutscher Bundestag und Bundesrat erkannt. Personen wurden in dem Beispieltext nicht erkannt. Die Frage, ob man “Sitz des Bundespräsidenten” als Ort (Sitz), Organisation (das Amt des Bundespräsidenten) und / oder Person (der Bundespräsident) bezeichnen sollte, hängt durchaus vom Anwendungsszenario ab.

OpeNER

Das OpeNER Projekt ist das Ergebnis eines europäischen Forschungsprojekts und erweitert die Funktionalität von DBpedia Spotlight mit weiteren semantischen Analysen. Die Demo unter http://demo2-opener.rhcloud.com/welcome.action (Tab “Live Analysis Demo“, “Named Entity Recognition and Classification” und “Named Entity Linking” auswählen und “Analyse” drücken, dann auf der rechten Seite das Tab “NERC” anwählen) ergibt für den gleichen Beispieltext:

opeNER-projekt

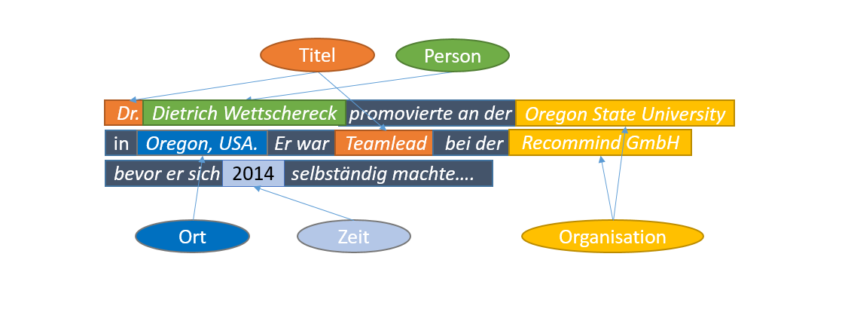
Abbildung 3: OpeNER Projekt (opener-project.eu)

Organisationen sind blau hinterlegt, während Orte orange markiert werden. Auch hier werden erkannte Entitäten mit ihren DBpedia Datenbankeinträgen verknüpft. Die Bedeutung dieser Verknüpfung erkennt man wenn man auf das Tab “Map” wechselt. Berlin wurde als Ort erkannt und über die Geo-Koordinaten (geo:long = 13.4083, geo.lat = 52.5186) im DBpedia Eintrag von Berlin konnte das Wort “Berlin” aus obigem Text automatisch auf der Weltkarte referenziert werden.

Es gibt eine Vielzahl weiterer Services für NLP wie z.B. OpenCalais. Einige dieser Services bieten bestimmte Funktionalitäten (wie z.B. Sentiment Analysis) oder andere Sprachen neben Englisch nur gegen eine Gebühr an.

Listen Tagger

Der Vollständigkeit halber sei noch erwähnt, dass in den meisten Anwendungsszenarien die oben genannten Werkzeuge durch sogenannte Listen-Tagger (englisch Dictionary Tagger) ergänzt werden. Diese Tagger verwenden Listen von Personen, Organisationen oder auch Marken, Bauteilen, Produktbezeichnern oder beliebigen anderen Gruppen von Entitäten. Listen-Tagger arbeiten entweder unabhängig von den oben genannten statistischen Taggern (wie z.B. dem Standford Tagger) oder nachgeschaltet. Im ersten Fall markieren diese Tagger alle Vorkommen bestimmter Worte im Text (z.B. „Zalando“ kann so direkt als Modemarke erkannt werden). Im zweiten Fall werden die Listen genutzt, um die statistisch erkannten Entitäten zu verifizieren. So könnte z.B. der Vorschlag des statistischen Taggers automatisch akzeptiert werden wenn die vorgeschlagene Person auch in der Liste gefunden wird. Ist die Person jedoch noch nicht in der Liste enthalten, dann könnte ein Mitarbeiter gebeten werden, diesen Vorschlag zu bestätigen oder zu verwerfen. Im Falle einer Bestätigung wird die neu erkannte Person dann in die Personenliste aufgenommen während sie im Falle einer Ablehnung in eine Negativliste übernommen werden könnte damit dieser Vorschlag in Zukunft automatisch unterdrückt wird.

Regular Expression Tagger

Manche Entitätstypen folgen klaren Mustern und können mit hoher Zuverlässigkeit durch reguläre Ausdrücke erkannt werden. Hierzu zählen z.B. Kreditkarten- oder Telefon- oder Versicherungsnummern aber auch in vielen Fällen Bauteilbezeichner oder andere firmeninterne Identifikatoren.

Fazit

Natural Language Processing und insbesondere Named Entity Recognition und Disambiguierung sollte Teil der Werkzeugkiste eines jeden Anwenders bei der Analyse von unstrukturierten Daten sein. Es existieren mehrere mächtige Toolkits und Services, die allerdings je nach Anwendungsgebiet kombiniert und verfeinert werden müssen. So erkennt DBpedia Spotlight nur Entitäten, die auch einen Wikipedia Eintrag haben, kann für diese aber reichhaltige Metadaten liefern. Der Stanford Tagger hingegen kann auch vollkommen unbekannte Personennamen aus dem textuellen Kontext erkennen, hat aber bei manchen Texten eine relativ hohe Falsch-Positiv-Rate. Eine Kombination der beiden Technologien und anwendungsspezifischen Listen von Entitäten kann daher zu qualitativ sehr hochwertigen Ergebnissen führen.

Benjamin Aunkofer

Interview – Data Science in der FinTech-Branche

/in , , , , , /by

Christian Rebernik ist CTO bei Number 26 und zuständig für die technische Entwicklung dieses FinTech-Unternehmens. Er studierte Informatik und Wirtschaftsinformatik und kann auf langjährige Erfahrung als Software-Entwickler zurückgreifen. Seit etwa 2010 war er als CTO und CIO bei diversen eCommerce-christian-rebernikUnternehmen, u.a. bei Immobilien.net (heute ImmobilienScout24), PARSHIP und Zanox, tätig und gilt daher als ein etablierter IT-Manager, der seine Kenntnisse als Mentor des Axel Springer Plug and Play Accelerators weitergibt.

Data Science Blog: Herr Rebernik, wie sind Sie als CTO zum FinTech Number26 gekommen?

Ich durfte die Gründer im Accelerator 2013 als Mentor begleiten. Damals war das Produkt ausgelegt auf Teenager als Zielgruppe. 2014 änderten die Gründer Valentin und Maximilian das Produkt auf Number26, ein mobile-first Gehaltskonto mit Mastercard und der Vision das weltbeste Bankerlebnis zu bieten. Damit hatten sie aus meiner Sicht den richtigen Nerv der Zeit getroffen. Mein Erfahrung mit Banken war nicht positiv bis dato. Number26 hat aus meiner Sicht das Potential Bankwesen zu verändern.

Data Science Blog: Die FinTech-Szene möchte vieles besser machen als traditionelle Banken. Welche Rolle spielt Data Science dabei?

Beim Online-Banking etablierter Banken erhält man meistens nur eine reine Ansicht des Bankkontos, quasi eine statische und nicht kundenorientierte Darstellung des Kontostandes und der Kontotransaktionen. Wir glauben, diese Auflistung ohne Intelligenz ist nicht ausreichend und wenig auf den Kundenutzen fokussiert, mit der heutigen Technik kann man deutlich mehr bieten.
Unser Ziel ist es, eine der besten Customer Experience zu schaffen. Dank moderner Technologien haben wir viele unterschiedliche Möglichkeiten, um das zu erreichen. Eine davon ist es Smart Banking anzubieten, hier kommt Data Science ins Spiel.

Data Science Blog: Wofür nutzt Number26 Data Science genau?

Wir starten in Sachen Data Science jetzt erst voll durch. Unser erster Data Scientist wurde letztes Jahr im Oktober eingestellt. Unser Team ist also noch im Aufbau. Aktuell steht die sichere und number26appautomatisierte Kategorisierung von Finanztransaktionen bei uns im Fokus. Damit bieten wir den Nutzern leicht verständliche und genaue Auswertungen ihrer finanziellen Situation sowie eine Übersicht ihrer Einnahmen und Ausgaben. Interessanterweise gibt es unseres Wissens nach noch keine Bank, die Transaktionen direkt für den Kundennutzen kategorisiert.
Abhängig von der Transaktionsart nutzen wir unterschiedliche Methoden des maschinellen Lernens, die wir für die Erkennung der übergeordneten Kategorie verwenden.

Data Science Blog: Welche Machine Learning Methoden kommen zum Einsatz? Und wo finden die Analysen statt?

Wir haben mehrere ML-Methoden ausprobiert und durch eine Prototyping-Phase hinsichtlich ihrer Treffgenauigkeit bewertet. Wir setzen auf Amazon Webservices (AWS) und nutzen das Amazon Machine Learning Framework, auf dem wir auch unsere Modelle testen und Algorithmen erstellen. Der Input ist beispielsweise eine Kontotransaktion.
Unsere Algorithmen versuchen dieses dann zu kategorisieren. Daraus gewinnen wir zusätzliche Informationen, die wir unseren Kunden als Mehrwert anbieten.
Handelt es sich um eine Peer-to-Peer-Transaktion, wenn beispielsweise ich einem Freund Geld überweise, parsen wir den Verwendungszweck und nutzen Textmustererkennung zur Kategorisierung der Überweisung. Dazu splitten wir den Überweisungstext in einzelne Wörter auf, deren Bedeutung über Wörterbücher erkannt werden. Dadurch entstehen Kategorien, die vom Nutzer auch manuell nachträglich geändert werden können. Dieses Nutzerfeedback fließt in den Algorithmus zurück und wird in zukünftige Kategorisierungen mit einbezogen. Wir arbeiten nach mehreren Experimenten nun vermehrt mit Vector Spacing Modellen, wie dem k-Nearest-Neighbour-Algorithmus, über zurzeit 12 Achsen (Vektordimensionen). Jeder Vektor stellt eine Eigenschaft einer Transaktion dar, beispielsweise Geldbetrag, Verwendungszweck, Empfänger oder Währung. Je näher die Eigenschaften, die im Vektorraum als Punkte dargestellt werden, an den Eigenschaften anderer Finanztransaktion im selben Vektorraum liegen, desto wahrscheinlicher ist die Gemeinsamkeit als Kategorie.
Natürlich gibt es immer wieder False-Positives, die die eigentliche Herausforderung in Data Science darstellen. Beispielsweise lassen sich seltene Transaktionen wie die Zahnarztrechnung nur schwer trainieren. Wir trainieren unsere Kategorisierung der Banktransaktionen unter Einbeziehung der MasterCard-Kreditkartentransaktionen. Alle Vertragspartner bei MasterCard müssen einige Angaben mahcen, z.B. welche Art von Händler sie sind, Das hilft natürlich bei der Kategorisierung.

Data Science Blog: Der Beruf des Data Scientist wurde schon öfter als„Sexiest Job des 21. Jahrhunderts“ zitiert, gilt das auch in der Finanzindustrie?

Wir als FinTech-Unternehmen sind technologiegetrieben und in unserer Branche macht es wirklich Spaß, Probleme des Finanzalltags zu lösen. Neue Lösungen anzubieten, auf die vorher noch niemand gekommen ist, ist zwar nicht jedermanns Sache, unser Schlag Menschen entwickelt aber genau dafür die größte Leidenschaft.

Data Science Blog: Was sind Ihrer Meinung nach die alltäglichen Aufgaben eines Data Scientists und welche Skills sollte ein Data Scientist dafür mitbringen?

Die Arbeit als Data Scientist ist meines Erachtens dreigeteilt: ein Drittel Datenaufbereitung, ein Drittel Software-Entwicklung und ein Drittel Analyse.
Zum ersten Drittel gehört die Sichtung der Daten und Identifikation der Datenqualität. Ein Data Scientist muss aber auch Software-Entwickler sein und ein Verständnis für Software-Architekturen mitbringen. Große Datenmengen lassen sich nur über skalierbare Anwendungen auswerten. Wichtige Hilfsmittel und Testumgebungen müssen dafür selbst entwickelt werden.
Für die Analyse ist ein gutes Verständnis von Mathematik unumgänglich. Hinzu kommt ein ausgezeichnetes Verständnis für das Kerngeschäft des Unternehmens, in unserem Fall das Finanzwesen, um dementsprechend relevante Analysen durchzuführen.

Dr. Stefan Kühn

Wie lernen Maschinen?

/in , , , , , , /by

Im dritten Teil meiner Reihe Wie lernen Maschinen? wollen wir die bisher kennengelernten Methoden anhand eines der bekanntesten Verfahren des Maschinellen Lernens – der Linearen Regression – einmal gegenüberstellen. Die Lineare Regression dient uns hier als Prototyp eines Verfahrens aus dem Gebiet der Regression, in weiteren Artikeln werden die Logistische Regression als Prototyp eines Verfahrens aus dem Gebiet der Klassifikation und eine Collaborative-Filtering- bzw. Matrix-Faktorisierungs-Methode als Prototyp eines Recommender-Systems behandelt.

Read more

Nico Hezel

KNN: Vorwärtspass

/in , , /by

Wenn die Gewichte eines künstlichen neuronalen Netzwerkes trainiert sind, kann es verwendet werden, um Vorhersagen über eine am Eingang angelegte Beobachtung zu treffen. Hierzu werden Schicht für Schicht, in einem sogenannten Vorwärtspass (Forward-Pass), die Aktivierungen der einzelnen Neuronen ermittelt, bis ein Ergebnis an der Ausgabeschicht anliegt. Der ganze Prozess hat zwar einen eigenen Namen (Vorwärtspass), ist aber im Endeffekt nur ein iteratives durchführen von mehreren logistischen Regressionen und entspricht dem Vorgehen aus dem Artikel „KNN: künstliche Neuronen“.

Anwendungsbeispiel

Im folgenden Beispiel verwenden wir die Wahrheitstabelle von einem X-OR Logikgatter (siehe Abbildungen unten links) als Ground Truth Data. Ziel ist es, den Ausgangwert Y, für einen beliebig anliegenden Eingangsvektor [X1, X2] vorherzusagen. Die Aufgabe ist recht komplex, so dass eine einfache lineare oder logistische Regression keine zufriedenstellende Lösung finden wird. Die zum Einsatz kommende  Netzwerkstruktur ist ein 2-schichtiges Feedforward Netzwerk mit zwei Eingangsneuronen, einer verborgenen Schicht und einem Ausgangsneuron.

XOR Wahrheitstabelle

X1 X2 Y = X1 ⊻ X2
0 0 0
0 1 1
1 0 1
1 1 0

 

Da das Netzwerk wie anfänglich erwähnt, bereits trainiert ist, gebe ich die Gewichte (Theta) vor. Werden die Werte als Matrix dargestellt, können mit Hilfe der linearen Algebra die Aktivierungswahrscheinlichkeiten aller Neuronen einer Schicht auf einmal ausgerechnet werden.

Theta 1

θ11 =  2,7 θ12 =   3,1
θ13 =  5,6 θ14 = -6
θ15 = -5,4 θ16 =  6,2
Theta 2

θ21 =  9,6
θ22 = -6,6
θ23 = -6,5

Programmcode

Für die eigentlichen Berechnungen verwenden wir die Programmiersprache Octave oder MATLAB. Octave ist eine kostenlose alternative zu MATLAB. Wobei es nicht notwendig ist irgendetwas zu installieren, da es auch eine Online Variante von MATLAB/Octave gibt:
http://www.tutorialspoint.com/execute_matlab_online.php

 %--------------------- Daten -----------------------
 X = [0 0;       		% Eingangsdaten
      0 1;
      1 0;
      1 1] 
     
 Y = [0;1;1;0] 			% erwartete XOR Ausgangsdaten


 theta1 = [2.7, 3.1; 	% antrainierte Gewichte der ersten Schicht
           5.6,  -6;
          -5.4, 6.2]
         
 theta2 = [9.6;			% antrainierte Gewichte der zweiten Schicht
          -6.6;
          -6.5]

 m = length(X)			% Anzahl der Eingangsdaten


 %--------------------- Vorwärtspass -----------------------
 V = X					% anlegen der Eingangsdaten an die Eingangsschicht

 % 1. berechne die Aktivierungen der verborgenen Schicht
 V = [ones(m,1) V]		% hinzufügen der Bias Units  (sind immer 1)
 Zv = V * theta1			% Summe aus den Eingangswerten multipliziert mit deren Gewichten
 H = 1 ./ (1 .+ e.^-Zv)	% anwenden der Sigmoid Funktion auf die Aktivierungsstärke Zv

 % 2. berechne die Aktivierungen der Ausgangsschicht
 H = [ones(m,1) H]		% hinzufügen der Bias Units an die verborgene Schicht
 Zh = H * theta2			% Produkt aus den Aktivierungen der Neuronen in H und Theta2
 O = 1 ./ (1 .+ e.^-Zh)	% Vorhersage von dem Netzwerk

 % 3. berechne die Vorhersageungenauigkeit
 loss = (O .- Y) .^ 2 	% quadratischer Fehler von der Vorhersage und der Zielvorgabe Y
 mse = sum(loss) / m		% durchschnittlicher quadratischer Fehler aller Vorhersagen

Ein paar Sätze zu den verwendeten Befehlen. Der Punkt vor manchen Operationen gibt an, dass die Operation Elementweise durchzuführen ist (wichtig bei der Sigmoid Funktion). Die Methode ones(M,N) erzeugt eine MxN große Matrix gefüllt mit den Werten 1. Wir erzeugen damit einen Spaltenvektor der unseren Bias Units entspricht und den wir anschließend an eine vorhandene Matrix horizontal anfügen.

Wird das Programm ausgeführt schreibt es unter anderem die Werte von der Ausgabeschicht O (Output Layer) auf die Konsole. Da wir alle XOR Variationen auf einmal ausgerechnet haben, erhalten wir auch vier Vorhersagen. Verglichen mit der Zielvorgaben Y sind die Werte von O sehr vielversprechend (ähnlich).

X1 X2 Y O
0 0 0 0.057099
0 1 1 0.936134
1 0 1 0.934786
1 1 0 0.050952

 

Komplexe Netzwerke

Hätte das Netzwerk noch weitere verborgene Schichten, müssen Teile des Programmcodes wiederholt ausgeführt werden. Grundsätzlich sind drei Befehle pro Schicht notwendig:

H1 = [ones(m,1) H1]			% hinzufügen der Bias Units an die verborgene Schicht
Zh1 = H1 * theta2			% Produkt aus den Aktivierungen der Neuronen in H1 und Theta2
H2 = 1 ./ (1 .+ e.^-Zh1)		% Aktivierungswahrscheinlichkeiten für die nächste verborgene Schicht

Im nächsten Artikel schauen wir uns das Training solcher Netzwerke an.

Dr. Stefan Kühn

Wie lernen Maschinen?

/in , , , /by

Im zweiten Teil wollen wir das mit Abstand am häufigsten verwendete Optimierungsverfahren – das Gradientenverfahren oder Verfahren des steilsten Abstiegs – anhand einiger Beispiele näher kennen lernen. Insbesondere werden wir sehen, dass die Suchrichtung, die bei der Benennung der Verfahren meist ausschlaggebend ist, gar nicht unbedingt die wichtigste Zutat ist.

Read more

Dr. Stefan Kühn

Wie lernen Maschinen?

/in , , , , /by

Machine Learning ist eines der am häufigsten verwendeten Buzzwords im Data-Science- und Big-Data-Bereich. Aber lernen Maschinen eigentlich und wenn ja, wie? In den meisten Fällen lautet die Antwort: Maschinen lernen nicht, sie optimieren. Fällt der Begriff Machine Learning oder Maschinelles Lernen, so denken viele sicherlich zuerst an bekannte “Lern”-Algorithmen wie Lineare Regression, Logistische Regression, Neuronale Netze oder Support Vector Machines. Die meisten dieser Algorithmen – wir beschränken uns hier vorerst auf den Bereich des Supervised Learning – sind aber nur Anwendungen einer anderen, grundlegenderen Theorie – der mathematischen Optimierung. Alle hier angesprochenen Algorithmen stellen dem Anwender eine bestimmte Ziel- oder Kostenfunktion zur Verfügung, aus der sich i.a. der Name der Methode ableitet und für die im Rahmen des Lernens ein Minimum oder Optimum gefunden werden soll. Ein großer Teil des Geheimnisses und die eigentliche Stärke der Machine-Learning-Algorithmen liegt nun darin, dass dieser Minimierungsprozess effizient durchgeführt werden kann. Wir wollen im Folgenden kurz erklären, wie dies in etwa funktioniert. In einem späteren Blogpost gehen wir dann genauer auf das Thema der Effizienz eingehen. Read more

Lukas Molzberger

Text-Mining mit dem Aika Algorithmus

/in , , , /by

In diesem Beitrag möchte ich das Open Source Projekt Aika vorstellen. Ziel des Projektes ist es einen Text-Mining Algorithmus zu entwickeln, der ein künstliches Neuronales Netz (kNN) mit einem Pattern Mining Algorithmus kombiniert. Dabei dient die Silbentrennung von Wörtern als initiale Aufgabe, anhand derer der Algorithmus weiterentwickelt wird. Für diese Aufgabe soll allerdings kein vordefiniertes Wörterbuch verwendet werden. Stattdessen sollen die Silben in ihrer Eigenschaft als häufig auftretende Muster in rohem Text erkannt werden. Hier reicht es allerdings nicht einen Mining Algorithmus nach häufig auftretenden Strings suchen zu lassen, da sich viele der Strings überlappen oder schlicht keinen Sinn ergeben würden. Es ist also wichtig, dass sich die erkannten Silben gegenseitig unterdrücken können und dass der Algorithmus in der Lage ist, die so entstehenden unterschiedlichen Interpretationen eines Wortes miteinander zu vergleichen und die am höchsten gewichtete auszuwählen. Beispielsweise taucht die Silbe ‘der’ zu Beginn des Wortes ‘de-re-gu-lie-ren’ auf. In diesem Fall muss der Algorithmus erkennen, dass die erste Silbe des Wortes nicht ‘der’ sondern nur ‘de’ ist.

Wenn nun nach häufig auftretenden Mustern in Text gesucht werden soll, warum verwenden wir nicht einen reinen Pattern Mining Algorithmus? Der Grund für die Kombination mit einem kNN liegt darin, dass die erkannten Muster innerhalb einer kNN Topologie aufeinander aufsetzen können. Wenn z. B. das Wort “hausboot” als Muster erkannt werden soll, dann entstünden in der Datenstruktur des Mining Algorithmus sehr viele Teilmuster, die alle evaluiert werden müssten. Viel leichter wäre es für den Algorithmus, wenn die Muster “haus” und “boot” bereits erkannt worden wären und nun als Eingaben für die Erkennung des Wortes “hausboot” dienen könnten. So ist der Algorithmus zum einen in der Lage komplexere Muster zu erkennen und muss gleichzeitig weniger Teilmuster untersuchen. Ausserdem erlaubt es ein kNN ‘weiche’ Muster zu erlernen, also Muster bei denen einzelne Eingänge optional sind, die aber trotzdem noch sicher erkannt werden. Dadurch kann eine höhere Toleranz gegenüber Fehlern erreicht werden.

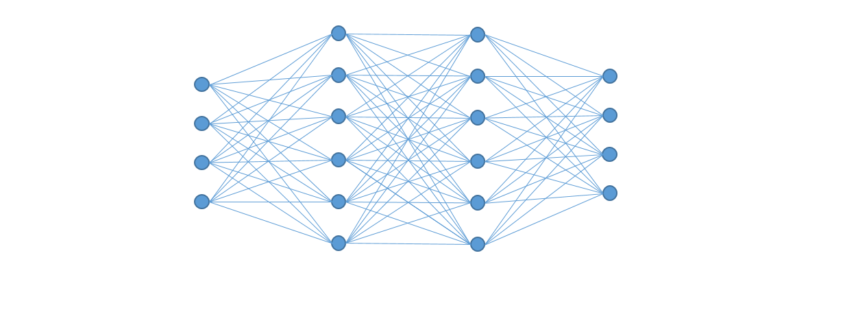
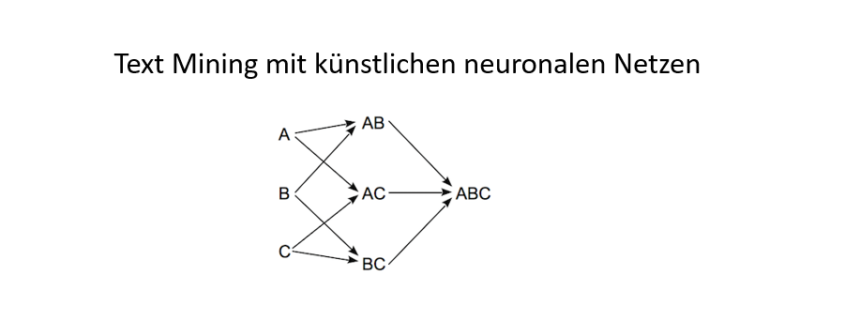
Im Gegensatz zu einem klassischen kNN nutzt Aika einen eher mit Googles Pagerank vergleichbaren Ansatz um Gewichte zwischen den einzelnen Neuronen des Netzwerks zu propagieren. Der Grutext-pattern-knnndgedanke dabei ist es, dass Neuronen entsprechend höher gewichtet werden sollten, wenn sie mit anderen hoch gewichteten Neuronen in Beziehung stehen. Wenn also beispielsweise eine Silbe in vielen hoch gewichteten Worten auftaucht, wird sie selbst entsprechend höher gewichtet.

Neuronen eines kNN erlauben es aber nicht nur Konjunktionen wie etwa bei Mustern zu erlernen, sondern auch Disjunktionen. Disjunktionen sind insbesondere beim Erlernen von Grammatikregeln wichtig, wenn z. B. einzelne Worte als Nomen erkannt werden sollen. Wenn nun solche Disjunktionen erlernt werden sollen, können auch hier häufige Muster behilflich sein. Angenommen, es wurden durch den Mining Algorithmus bereits die folgenden häufigen Muster gefunden: “der Baum” (f=4), “der Hammer” (f=3) und “der Nagel” (f=6). Dann können diese Muster so umgeformt werden, dass ein neues, deutlich häufigeres Muster “der <NOMEN>” (f=13) und eine Disjunktion <NOMEN> = “Baum” oder “Hammer” oder “Nagel”, entsteht.

Radek Mackowiak

KNN: Natur als Vorbild – Biologische Neuronen

/in , , , , /by

Bisher ist die genaue Funktionsweise des Gehirns bei der Verarbeitung sensorischer Informationen nicht bekannt. Neue Erkenntnisse im Bereich der Neurowissenschaften liefern jedoch einen Einblick über grundlegende Prinzipien wie das Gehirn von Säugetieren sensorische Informationen repräsentiert. Einer der wichtigsten Punkte ist dabei die Erkenntnis, dass der Neocortex, einem ankommenden Signal erlaubt ein komplexes Netzwerk von Neuronen zu durchlaufen, wodurch es zu einer abstrakten Repräsentation des ursprünglichen Eingabesignals kommt. Auch ist das Gehirn in der Lage die Leitfähigkeit der Verbindungen zwischen den Neuronen zu modifizieren, was sich auf eine Änderung der Abbildungsvorschrift auswirkt. Beobachtungen können dadurch noch besser getrennt und effizienter repräsentiert werden. Die Entdeckung dieses Verhaltens motivierte die Entstehung des Forschungszweiges Deep Machine Learning, welcher sich darauf fokussiert Modelle zu entwickeln, die ähnliche Charakteristiken wie der Neocortex aufweisen.

Das Eingabesignal durchläuft das Netzwerk bis zu einer Ausgabeschicht. Das Resultat dieser nicht linearen Transformation lässt sich dann beispielsweise mit einem Klassifizierungsalgorithmus auswerten. Die praktischen Anwendungen solcher Algorithmen sind sehr vielfältig. Deep Machine Learning Algorithmen liefern zurzeit die besten Ergebnisse zu vielen Problemen in Anwendungsdomänen wie Bilderkennung, Spracherkennung und der Verarbeitung natürlicher Sprache. Mit Hilfe dieser Algorithmen wurden beispielsweise neue elementare Teilchen gefunden, entdeckte Galaxien noch besser klassifiziert und Auswirkungen von Mutationen innerhalb von DNA vorhergesagt.

Das Neuron

Das Neuron ist die Basis-Recheneinheit des Gehirns. Ungefähr 86 Milliarden solcher Neuronen befinden sich im menschlichen Nervensystem, welche durch ca. 10^15 Synapsen miteinander vermascht sind. In Abbildung unten links wird eine Schemazeichnung eines biologischen Neurons dargestellt. Dieses besteht unter Anderem aus Dendriten, dem Zellkörper, der den Zellkern beinhaltet und einem Axon. Die Dendriten gehen aus dem Zellkörper hervor und sind über Synapsen mit sensorischen Zellen oder Axonen anderer Neuronen verbunden. Ihre Aufgabe ist die Aufnahme von ankommenden Signalen in Form von elektrischen Spannungsänderungen und der Transport dieser in den Zellkörper des Neurons, der Recheneinheit einer Nervenzelle. Dort angekommen entscheiden bestimmte Faktoren, ob ein Aktionspotential anhand einer Schwellwertfunktion ausgelöst wird oder nicht. Ist dies der Fall leitet das Neuron elektrische Energie über sein Axon an weitere angeschlossene Dendriten anderer Neuronen weiter.

Neuronen
Das biologische Neuron diente als Inspiration für das Software-Neuron. Beim mathematischen Modell eines Software-Neurons (Künstliches Neuron eines KNN) wird davon ausgegangen, dass die verschiedenen Dendriten unterschiedlich stark ausgeprägt sind und ein Signal daher auch verschieden stark gewichtet in den Zellkörper übertragen wird. Jedes Dendrit enthält demnach einen Faktor(θi), der das Signal(xi) vor dem Eintreffen in den Zellkörper skaliert (θixi). Diese Faktoren werden auch als Gewichte bezeichnet. Im Zellkörper selbst werden die Signale die von unterschiedlichen Neuronen stammen aufsummiert bis schließlich ein fester Bias-Wert(b) auf das Ergebnis der Summation aufaddiert wird. Anschließend bestimmt eine nicht-lineare Aktivierungsfunktion über den finalen Ausgangswert des Neurons.

Bildquelle: Wikipedia

Ähnliche Artikel:

Nico Hezel

KNN: Künstliche Neuronen

/in , , /by

Es gibt sehr ausführliche Definitionen und Abbildungen für ein künstliches Neuron, die in diesem Artikel aber nicht behandelt werden. Der Grund dafür ist pragmatischer Natur. Es soll eine gewisse Konsistenz zu den anderen KNN-Beiträgen dieser Reihe bestehen und das Thema soll nicht zu einer wissenschaftlichen Abhandlung mutieren.

In dem Beitrag  KNN: Was sind künstliche neuronale Netze  geht es um den grundsätzlichen Aufbau von künstlichen neuronalen Netzwerken. Zusammengesetzt werden die Strukturen aus einer oftmals großen Anzahl von künstlichen Neuronen. Die nachfolgende Abbildung zeigt auf der Linken Seite einen extrahierten Ausschnitt aus einem Netzwerk. Es kann auch als einfaches allein stehendes Netzwerk betrachtet werden. Auf der rechten Seite ist eine allgemeingültigere Form zu sehen. Die Bias Unit (VB) wird üblicherweise als X0 bezeichnet und hat immer den Wert 1.

 

neuronen-netzwerk1 neuronen-netzwerk2

 


Um den Ausgangswert Y zu berechnen wird zunächst jeder Eingangswert X mit seinem dazugehörigen Gewicht theta (Theta) multipliziert und die Ergebnisse aufsummiert. Das Zwischenergebnis ist die Aktivierungsstärke z:
[
z = X_0 cdot theta_0 + X_1 cdot theta_1 + X_2 cdot theta_2
]

Im nächsten Schritt wird der eigentliche Ausgangswert Y errechnet, indem die Aktivierungsstärke z an eine Aktivierungsfunktion angelegt wird. Es gibt zwar verschiedene Funktionen, häufig wird aber die Logistische bzw. Sigmoid-Funktion verwendet. Sie ist nicht-linear und hat einen Ausgangswertebereich zwischen 0 und 1.

sigmoid-funktion [
sigmoid(z) = frac{1}{1+e^{-z}}
]

Wird das Bias Neuron und sein Gewicht nicht beachtet, bestimmen die eingehenden Daten die Aktivierungsstärke und damit den Ausgang der Funktion. Unter Verwendung der Bias Unit verschiebt sich die Funktion entlang der Y-Achse, was einer Verschiebung von einem Schwellwert gleich kommt.

Die endgültige Formel für die Aktivierung eines Neurons sieht sehr ähnlich zu der Logistischen Regression aus. Werden die Werte von X und Theta zu Vektoren zusammengefasst, lässt sich die Berechnung stark vereinfachen:
[
Y = sigmoid(Xtheta)
]

Als Programmcode müsste diese Berechnung dennoch mit einer Schleife realisiert werden oder noch besser mit einer Bibliothek für lineare Algebra.

Ähnliche Artikel:
• KNN: Was sind künstliche neuronale Netze
• KNN: Vorteile und Nachteile

Nico Hezel

KNN: Vorteile und Nacheile

/in , , , , /by

Wie jedes Verfahren haben auch künstliche Neuronale Netzwerke (KNN) ihre Vor- und Nachteile. Im Folgenden sollen einige benannt werden.

Vorteile

  • KNN können bessere Ergebnisse liefern als existierende statistische Ansätze, wenn das Problem ausreichend komplex ist. Das heißt, wenn das Problem nicht linear ist und es viele Eingabedaten mit vielen Variablen gibt.
  • Es gibt zwar sogenannte Hyperparameter, die je nach Einstellung das Netzwerk besser oder schlechter trainieren lassen, diese müssen aber nur manuell geändert werden, wenn neue Rekordwerte erreicht werden sollen. Ansonsten gibt es verhältnismäßig wenige Parameter.
  • Auch für stark nicht lineare Probleme, werden gute Lösungen gefunden. Dazu zählen fast alle Probleme die aus einer Datenbasis stammen, wo menschliche oder andere unvorhersehbare Einflüsse wirken.
  • Für große Datenmengen und viele Datendimensionen (Einflussfaktoren) können sinnvolle Ergebnisse ermittelt werden.

Nachteile

  • Künstliche Neuronale Netzwerke sind oftmals wie eine Blackbox. Dadurch ist es nicht möglich nachzuverfolgen wieso ein Netzwerk eine bestimmte Entscheidung getroffen hat.
  • Damit ein allgemeingültiges gutes Ergebnis berechnet werden kann, bedarf es vieler Beispiel-/Trainingsdaten.
  • Aufgrund der hohen Datenmenge, ist es sinnvoll die Berechnungen auf einer Grafikkarte durchzuführen.
  • Während des Trainings finden sehr viele Gewichtsänderungen in kurzer Zeit statt. Daher ist ein Aufteilen der Arbeit in ein verteiltes System wie Apache Hadoop oder Apache Spark nur schwer möglich und führt oftmals zu drastischen Performanz Einbußen.
  • Ist das Problem mathematisch beschreibbar sind KNNs oftmals schlechter oder maximal genauso gut.
  • Es ist zu keinen Zeitpunkt bekannt ob die gefundene Lösung das globale Optimum ist oder ob es noch bessere Lösungen gibt.

In der Forschung gibt es viele Ansätze um einige der Nachteile aufzuheben.