Einführung in die Welt der Autoencoder
An wen ist der Artikel gerichtet?
In diesem Artikel wollen wir uns näher mit dem neuronalen Netz namens Autoencoder beschäftigen und wollen einen Einblick in die Grundprinzipien bekommen, die wir dann mit einem vereinfachten Programmierbeispiel festigen. Kenntnisse in Python, Tensorflow und neuronalen Netzen sind dabei sehr hilfreich.
Funktionsweise des Autoencoders
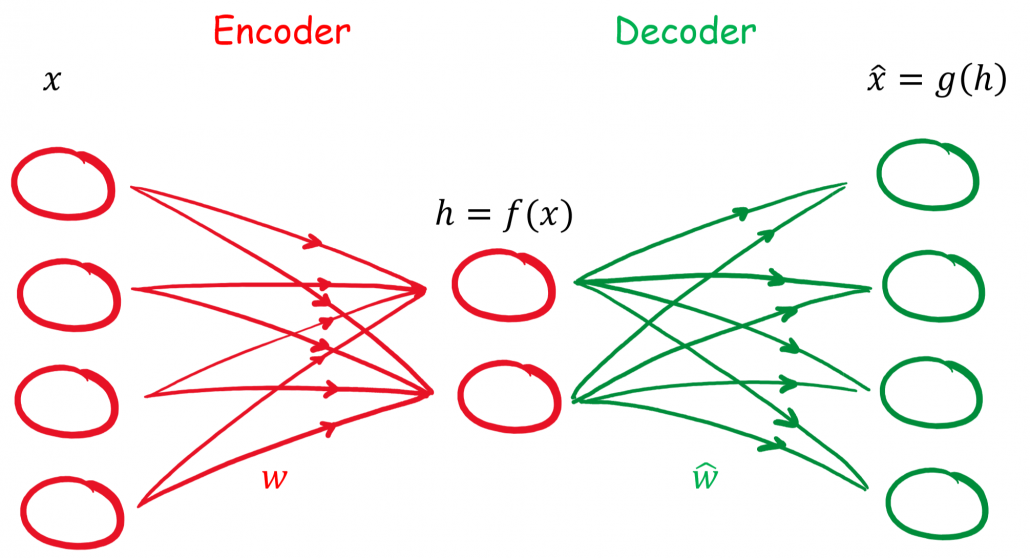
Ein Autoencoder ist ein neuronales Netz, welches versucht die Eingangsinformationen zu komprimieren und mit den reduzierten Informationen im Ausgang wieder korrekt nachzubilden.
Die Komprimierung und die Rekonstruktion der Eingangsinformationen laufen im Autoencoder nacheinander ab, weshalb wir das neuronale Netz auch in zwei Abschnitten betrachten können.
Der Encoder
Der Encoder oder auch Kodierer hat die Aufgabe, die Dimensionen der Eingangsinformationen zu reduzieren, man spricht auch von Dimensionsreduktion. Durch diese Reduktion werden die Informationen komprimiert und es werden nur die wichtigsten bzw. der Durchschnitt der Informationen weitergeleitet. Diese Methode hat wie viele andere Arten der Komprimierung auch einen Verlust.
In einem neuronalen Netz wird dies durch versteckte Schichten realisiert. Durch die Reduzierung von Knotenpunkten in den kommenden versteckten Schichten werden die Kodierung bewerkstelligt.
Der Decoder
Nachdem das Eingangssignal kodiert ist, kommt der Decoder bzw. Dekodierer zum Einsatz. Er hat die Aufgabe mit den komprimierten Informationen die ursprünglichen Daten zu rekonstruieren. Durch Fehlerrückführung werden die Gewichte des Netzes angepasst.
Ein bisschen Mathematik
Das Hauptziel des Autoencoders ist, dass das Ausgangssignal dem Eingangssignal gleicht, was bedeutet, dass wir eine Loss Funktion haben, die L(x , y) entspricht.
Unser Eingang soll mit x gekennzeichnet werden. Unsere versteckte Schicht soll h sein. Damit hat unser Encoder folgenden Zusammenhang h = f(x).
Die Rekonstruktion im Decoder kann mit r = g(h) beschrieben werden. Bei unserem einfachen Autoencoder handelt es sich um ein Feed-Forward Netz ohne rückkoppelten Anteil und wird durch Backpropagation oder zu deutsch Fehlerrückführung optimiert.
| Formelzeichen | Bedeutung |
 |
Eingangs-, Ausgangssignal |
 |
Gewichte für En- und Decoder |
 |
Bias für En- und Decoder |
 |
Aktivierungsfunktion für En- und Decoder |
 |
Verlustfunktion |
Unsere versteckte Schicht soll mit 
gekennzeichnet werden. Damit besteht der Zusammenhang:
(1) ![\begin{align*} \mathbf{h} &= f(\mathbf{x}) = \sigma(\mathbf{W}\mathbf{x} + \mathbf{B}) \\ \hat{\mathbf{x}} &= g(\mathbf{h}) = \hat{\sigma}(\hat{\mathbf{W}} \mathbf{h} + \hat{\mathbf{B}}) \\ \hat{\mathbf{x}} &= \hat{\sigma} \{ \hat{\mathbf{W}} \left[\sigma ( \mathbf{W}\mathbf{x} + \mathbf{B} )\right] + \hat{\mathbf{B}} \}\\ \end{align*}](https://data-science-blog.com/de/wp-content/ql-cache/quicklatex.com-96b9128bd26ff4d2975a372d338e15c4_l3.png "Rendered by QuickLaTeX.com")
Für eine Optimierung mit der mittleren quadratischen Abweichung (MSE) könnte die Verlustfunktion wie folgt aussehen:
(2) ![\begin{align*} L(\mathbf{x}, \hat{\mathbf{x}}) &= \mathbf{MSE}(\mathbf{x}, \hat{\mathbf{x}}) = \| \mathbf{x} - \hat{\mathbf{x}} \| ^2 &= \| \mathbf{x} - \hat{\sigma} \{ \hat{\mathbf{W}} \left[\sigma ( \mathbf{W}\mathbf{x} + \mathbf{B} )\right] + \hat{\mathbf{B}} \} \| ^2 \end{align*}](https://data-science-blog.com/de/wp-content/ql-cache/quicklatex.com-2afadab2e44942274d566bd163b513cf_l3.png "Rendered by QuickLaTeX.com")
Wir haben die Theorie und Mathematik eines Autoencoder in seiner Ursprungsform kennengelernt und wollen jetzt diese in einem (sehr) einfachen Beispiel anwenden, um zu schauen, ob der Autoencoder so funktioniert wie die Theorie es besagt.
Dazu nehmen wir einen One Hot (1 aus n) kodierten Datensatz, welcher die Zahlen von 0 bis 3 entspricht.
![\begin{align*} [1, 0, 0, 0] \ \widehat{=} \ 0 \\ [0, 1, 0, 0] \ \widehat{=} \ 1 \\ [0, 0, 1, 0] \ \widehat{=} \ 2 \\ [0, 0, 0, 1] \ \widehat{=} \ 3\\ \end{align*}](https://data-science-blog.com/de/wp-content/ql-cache/quicklatex.com-072135e2e36d72e0e3bf860c5308e03a_l3.png "Rendered by QuickLaTeX.com")
Diesen Datensatz könnte wie folgt kodiert werden:
![\begin{align*} [1, 0, 0, 0] \ \widehat{=} \ 0 \ \widehat{=} \ [0, 0] \\ [0, 1, 0, 0] \ \widehat{=} \ 1 \ \widehat{=} \ [0, 1] \\ [0, 0, 1, 0] \ \widehat{=} \ 2 \ \widehat{=} \ [1, 0] \\ [0, 0, 0, 1] \ \widehat{=} \ 3 \ \widehat{=} \ [1, 1] \\ \end{align*}](https://data-science-blog.com/de/wp-content/ql-cache/quicklatex.com-17422530a780bd436a53fc45b2a523aa_l3.png "Rendered by QuickLaTeX.com")
Damit hätten wir eine Dimensionsreduktion von vier auf zwei Merkmalen vorgenommen und genau diesen Vorgang wollen wir bei unserem Beispiel erreichen.
Programmierung eines einfachen Autoencoders
Typische Einsatzgebiete des Autoencoders sind neben der Dimensionsreduktion auch Bildaufarbeitung (z.B. Komprimierung, Entrauschen), Anomalie-Erkennung, Sequenz-to-Sequenz Analysen, etc.
Ausblick
Wir haben mit einem einfachen Beispiel die Funktionsweise des Autoencoders festigen können. Im nächsten Schritt wollen wir anhand realer Datensätze tiefer in gehen. Auch soll in kommenden Artikeln Variationen vom Autoencoder in verschiedenen Einsatzgebieten gezeigt werden.
About Author
Leave a Reply
Want to join the discussion?Feel free to contribute!