Benford-Analyse
Das Benfordsche Gesetz beschreibt eine Verteilung der Ziffernstrukturen von Zahlen in empirischen Datensätzen. Dieses Gesetz, welches kein striktes Naturgesetz ist, sondern eher ein Erklärungsversuch in der Natur und in der Gesellschaft vorkommende Zahlenmuster vorherzusagen.
Das Benfordsche Gesetz beruht auf der Tatsache, dass die Ziffern in einem Zahlensystem hierarchisch aufeinander aufbauen: Es beginnt mit der 1, dann folgt die 2, dann die 3 usw. In Kombination mit bestimmten Gesetzen der Natur (der natürliche Wachstumsprozess, dabei möglichst energiesparend wachsen/überleben) oder Ökonomie (so günstig wie möglich einkaufen) ist gemäß des Benfordschen Gesetz zu erwarten, dass die Ziffer 1 häufiger vorkommt als die 2, die wiederum häufiger vorkommt als die 3. Die Ziffer 9 braucht demnach den längsten Weg und kommt entsprechend verhältnismäßig seltener vor.
Dieses Phönomen hilft uns bei echten Zufallszahlen nicht weiter, denn dann sind alle Ziffern nicht aufeinander aufbauend, sondern mehr oder weniger gleichberechtigt in ihrem Auftrauen. Bei der klassischen und axiomatischen Wahrscheinlichkeit kommen wir damit also nicht ans Ziel.
Die Benford-Analyse ist im Grunde eine Ausreißeranalyse: Wir vergleichen Ziffernmuster in Datenbeständen mit der Erwartungshaltung des Benfordschen Gesetzes. Weicht das Muster von dieser Erwartung ab, haben wir Diskussionsbedarf.
Moderne Zahlensysteme sind Stellenwert-Zahlensysteme. Neben den Dual-, Oktal- und Hexadezimalzahlensystemen, mit denen sich eigentlich nur Informatiker befassen, wird unser Alltag vom Dezimalzahlensystem geprägt. In diesem Zahlensystem hat jede Stelle die Basis 10 (“dezi”) und einen Exponenten entsprechend des Stellenwertes, multipliziert mit der Ziffer d. Es ist eine Exponentialfunktion, die den Wert der Ziffern in bestimmter Reihenfolge ermittelt:
![]()
Die Benford-Analyse wird meistens nur für die erste Ziffer (also höchster Stellenwert!) durchgeführt. Dies werden wir gleich einmal beispielhaft umsetzen.
Die Wahrscheinlichkeit des Auftretens der ersten “anführenden” Ziffer d ist ein Logarithmus zur Basis B. Da wir im alltäglichen Leben – wie gesagt – nur im Dezimalzahlensystem arbeiten, ist für uns B = 10.
![]()
Im Standard-Python lässt sich diese Formel leicht mit einer Schleife umsetzen:
import math [round(math.log10(1+1/float(i))*100.0, 2) for i in range(1,10)] Out: [30.1, 17.61, 12.49, 9.69, 7.92, 6.69, 5.8, 5.12, 4.58]
Benford-Algorithmus in Python mit NumPy und Pandas
Nachfolgend setzen wir eine Benford-Analyse als Minimalbeispiel in NumPy und Pandas um.
import numpy as np
x = np.arange(1,10) # NumPy-Array erstellen
x
Out: array([ 1, 2, 3, 4, 5, 6, 7, 8, 9])
benford = np.round(np.log10(1+1/x) * 100.0, decimals=2) # Den Logarithmus auf das NumPy-Array anwenden und runden
Out: array([ 30.1 , 17.61, 12.49, 9.69, 7.92, 6.69, 5.8 , 5.12,
4.58])
Nun möchten wir eine Tabelle erstellen, mit zwei Spalten, eine für die Ziffer (Digit), die andere für die relative Häufigkeit der Ziffer (Benford Law). Dazu nutzen wir das DataFrame aus dem Pandas-Paket. Das DataFrame erstellen wir aus den zwei zuvor erstellten NumPy-Arrays.
import pandas as pd
benfordFrame = pd.DataFrame({'Digit': x, 'Benford Law': benford})
benfordFrame
Out:
Benford Law Digit
0 30.10 1
1 17.61 2
2 12.49 3
3 9.69 4
4 7.92 5
5 6.69 6
6 5.80 7
7 5.12 8
8 4.58 9
Man könnte sicherlich auch den natürlichen Index des DataFrames nutzen, indem wir diesen nur um jeweils 1 erhöhen, aber das verwirrt später nur und tun wir uns jetzt daher lieber nicht an…
benfordFrame.plot('Digit', 'Benford Law', kind='bar', title='Benford', legend=False)
Das Dataframe-Objekt kann direkt plotten (das läuft über die matplotlib, die wir aber nicht direkt einbinden müssen):
Diese neun Balken zeigen die Verteilung der Ziffernhäufigkeit nach dem Benfordschen Gesetz, diese Verteilung ist unsere Erwartungshaltung an andere nummerische Datenbestände, wenn diese einem natürlichen Wachstum unterliegen.
Analyse der Verteilung der ersten Ziffer in Zahlungsdaten
Jetzt brauchen wir Daten mit nummerischen Beträgen, die wir nach Benford testen möchten. Für dieses Beispiel nehme ich aus einem ein SAP-Testdatensatz die Spalte ‘DMBTR’ der Tabelle ‘BSEG’ (SAP FI). Die Spalte ‘DMBTR’ steht für “Betrag in Hauswährung’, die ‘BSEG’ ist die Tabelle für die buchhalterischen Belegsegmente.
Die Datei mit den Testdaten ist über diesen Link zum Download verfügbar (Klick) und enthält 40.000 Beträge.
Wir laden den Inhalt der Datei via NumPy.LoadTxt() und machen aus dem resultierenden NumPy-Array wieder ein Pandas.DataFrame und holen uns die jeweils erste Ziffer für alle Einträge als Liste zurück.
financialTransactions = np.loadtxt("[DEIN LOKALER PFAD]\BSEG_DMBTR.csv", skiprows=1)
financialTransactionsFrame = pd.DataFrame({'Zahlungen':financialTransactions})
firstDigits = [str(value)[0:1] for value in financialTransactionsFrame['Zahlungen']]
Die Einträge der ersten Ziffer in firstDigits nehmen wir uns dann vor und gruppieren diese über die Ziffer und ihrer Anzahl relativ zur Gesamtanzahl an Einträgen.
percentDigits = np.asarray([[i, firstDigits.count(str(i))/float(len(financialTransactionsFrame['Zahlungen']))*100] for i in range(1, 10)]) percentDigits.T[1].sum() Out: 94.0
Wenn wir die Werte der relativen Anzahl aufsummieren, landen wir bei 94% statt 100%. Dies liegt daran, dass wir die Ziffer 0 ausgelassen haben, diese jedoch tatsächlich vorkommt, jedoch nur bei Beträgen kleiner 1.00. Daher lassen wir die Ziffer 0 außenvor. Wer jedoch mehr als nur die erste Ziffer prüfen möchte, wird die Ziffer 0 wieder mit in die Betrachtung nehmen wollen. Nur zur Probe nocheinmal mit der Ziffer 0, so kommen wir auf die 100% der aufsummierten relativen Häufigkeiten:
percentDigits = np.asarray([[i, firstDigits.count(str(i))/float(len(financialTransactionsFrame['Zahlungen']))*100] for i in range(0, 10)]) percentDigits.T[1].sum() Out: 100.0
Nun erstellen wir ein weiteres Pandas.DataFrame, mit zwei Spalten: Die Ziffern (Digit) und die tatsächliche Häufigkeit in der Gesamtpopulation (Real Distribution):
percentDigitsFrame = pd.DataFrame({'Digit':percentDigits[:,0], 'Real Distribution':percentDigits[:,1]})
Abgleich der Ziffernhäufigkeit mit der Erwartung
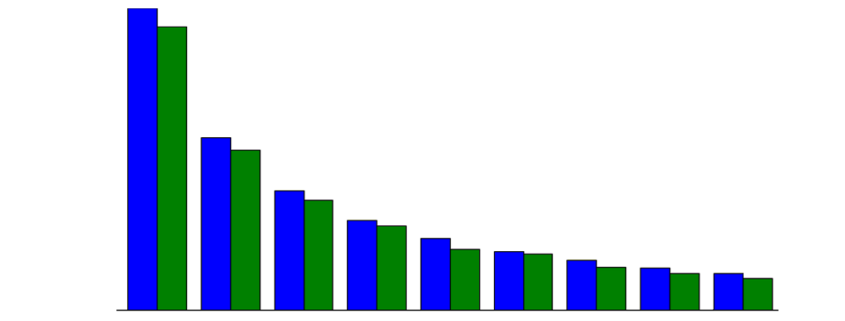
Nun bringen wir die theoretische Verteilung der Ziffern, also nach dem zuvor genannten Logarithmus, und die tatsächliche Verteilung der ersten Ziffern in unseren Zahlungsdaten in einem Plot zusammen:
import matplotlib.pyplot as pyplot
fig = pyplot.figure()
ax = fig.add_subplot(111)
ax2 = ax.twinx()
percentDigitsFrame.plot('Digit', 'Real Distribution', kind='bar', ax=ax2, width = 0.4, color="green", position=0, legend=False)
benfordFrame.plot('Digit', 'Benford Law', kind='bar', ax=ax, width = 0.4, color="blue", position=1, legend=False)
lines, labels = ax.get_legend_handles_labels()
lines2, labels2 = ax2.get_legend_handles_labels()
ax2.legend(lines + lines2, labels + labels2, loc=0)
ax.set_ylim(1,35)
ax2.set_ylim(1,35)
pyplot.show()
In dem Plot wird deutlich, dass die Verteilung der führenden Ziffer in unseren Zahlungsdaten in ziemlich genau unserer Erwartung nach dem Benfordschen Gesetz entspricht. Es sind keine außerordentlichen Ausreißer erkennbar. Das wäre auch absolut nicht zu erwarten gewesen, denn der Datensatz ist mit 40.000 Einträgen umfassend genug, um dieses Muster gut abbilden zu können und von einer Manipulation dieser Beträge im SAP ist ebenfalls nicht auszugehen.
Gegenüberstellung: Computer-generierte Zufallszahlen
Jetzt wollen wir nochmal kurz darauf zurück kommen, dass das Benfordsche Gesetz für Zufallszahlen nicht unwendbar ist. Bei echten Zufallszahlen bin ich mir da auch sehr sicher. Echte Zufallszahlen ergeben sich beispielweise beim Lotto, wenn die Bälle mit Einzel-Ziffern durch eine Drehkugel hüpfen. Die Lottozahl-Ermittlung erfolgt durch die Zusammenstellung von jeweils gleichberechtigt erzeugten Ziffern.
Doch wie ist dies bei vom Computer generierten Zufallszahlen? Immerhin heißt es in der Informatik, dass ein Computer im Grunde keine Zufallszahlen erzeugen kann, sondern diese via Takt und Zeit erzeugt und dann durchmischt. Wir “faken” unsere Zahlungsdaten nun einfach mal via Zufallszahlen. Hierzu erstellen wir in NumPy ein Array mit 2000 Einträgen einer Zufallszahl (NumPy.Random.rand(), erzeugt floats 0.xxxxxxxx) und multiplizieren diese mit einem zufälligen Integer (Random.randint()) zwischen 0 und 1000.
from random import randint financialTransactions = np.round(np.random.rand(2000) * randint(0,1000),decimals=2) # Zufallszahlen erzeugen, die auf dem ersten Blick als Zahlungsdaten durchgehen :-)
Erzeugen wir die obigen Datenstrukturen erneut, zeigt sich, dass die Verteilung der Zufallszahlen ganz anders aussieht: (vier unterschiedliche Durchläufe)
Anwendung in der Praxis
Data Scientists machen sich das Benfordsche Gesetz zu Nutze, um Auffälligkeiten in Zahlen aufzuspüren. In der Wirtschaftsprüfung und Forensik ist diese Analyse-Methode recht beliebt, um sich einen Eindruck von nummerischen Daten zu verschaffen, insbesondere von Finanztransaktionen. Die Auffälligkeit durch Abweichung vom Benfordchen Gesetz entsteht z. B. dadurch, dass Menschen eine unbewusste Vorliebe für bestimmte Ziffern oder Zahlen haben. Greifen Menschen also in “natürliche” Daten massenhaft (z. B. durch Copy&Paste) ein, ist es wahrscheinlich, dass sie damit auch vom Muster des Benfordschen Gesetzes abweichen. Weicht das Muster in Zahlungsströmen vom Bendfordsche Erwartungsmuster für bestimmte Ziffern signifikant ab, könnte dies auf Fälle von unnatürlichen Eingriffen hindeuten.
Die Benford-Analyse wird auch gerne eingesetzt, um Datenfälschungen in wissenschaftlichen Arbeiten oder Bilanzfälschungen aufzudecken. Die Benford-Analyse ist dabei jedoch kein Beweis, sondern liefert nur die Indizien, die Detailanalysen nach sich ziehen können/müssen.