3D-Visualisierung von Graphen
Die Graphentheorie ist ein wichtiger Teil vieler Methoden und Anwendungsgebiete für Big Data Analytics. Graphen sind mathematisch beschreibbare Strukturen, ohne die im Ingenieurwesen nichts funktionieren würde. Ein Graph besteht aus zwei Knoten (Ecken, engl. Vertex), die über eine Kante (engl. Edge) verbunden sind.
Auf Graphen stoßen Data Scientists beispielsweise bei der Social Media Analyse, beim Aufbau von Empfehlungssystemen (das Amazon-Prinzip) oder auch bei Prozessanalysen (Process Mining). Aber auch einige Big Data Technologien setzen ganz grundlegend auf Graphen, beispielsweise einige NoSQL-Datenbanken wie die Graphendatenbank Neo4j und andere.
Graphen können nicht nur einfache Verkettungen, sondern komplexe Netzwerke abbilden. Das Schöne daran ist, dass Graphen nicht ganz so abstrakt sind, wie viele andere Bereiche der Mathematik, sondern sich wunderbar visualisieren lassen und wir auch in unserem Vorstellungsvermögen recht gut mit ihnen “arbeiten” können.

Mit der Visualisierung von Graphen, können wir uns Muster vor Augen führen und ein visuelles Data Mining betreiben. Iterative und auch rekursive Vorgänge sowie Abhängigkeiten zwischen einzelnen Objekten/Zuständen können visuell einfach besser verstanden werden. Bei besonders umfangreichen und zugleich vielfältigen Graphen ist eine Visualisierung in drei bzw. vier Dimensionen (x-, y-, z-Dimensionen + Zeit t) nicht nur schöner anzusehen, sondern kann auch sehr dabei helfen, ein Verständnis (z. B. über Graphen-Cluster) zu erhalten.
3D-Animation von Graphen mit Python und UbiGraph
Mit dem Open Source Projekt UbiGraph lassen sich Graphen dreidimensional visualisieren. UbiGraph bietet APIs zu den Programmiersprachen C, C++, Java, Ruby, Perl und Python.
UbiGraph funktioniert nur auf unix-basierten Systemen und leider (noch?) nicht auf Microsoft Windows. Wer also auf Windows unterwegs ist, der benötigt eine Virtual Machine. In meinem Fall läuft es wunderbar in einer Virtual Box (zugewiesen: SSD Festplatte, 4G RAM, Grafikspeicher 768 MB) mit dem auf Debian basierenden Linux Mint ohne Probleme.
Benötigt wird ferner Python 2.7 (in den meisten Linux-Distributionen bereits enthalten) und UbiGraph, welches über diesen Link heruntergeladen werden kann.
Nach dem Herunterladen des Paketes, dieses einfach mit
[box]tar xvf [Ubigraph-Paket][/box]
entpacken, in das entpackte Verzeichnis wechseln und [box]bin/ubigraph_server &[/box] ausführen.
Folgender Fehler könnte die Euphorie beim Starten des UbiGraph-Servers etwas bremsen:
[box]./UbiGraph-alpha-0.2.4-Linux32-Ubuntu-8.04/bin/ubigraph_server: error while loading shared libraries: libglut.so.3: cannot open shared object file: No such file or directory.[/box]
Allerdings bedeutet dieser Fehler in der Regel, dass freeglut3 fehlt, also mit folgendem Befehl (Ubuntu/Debian) nachinstallieren:
[box]apt-get install freeglut3[/box]
Prüfen ob der Server läuft (der UbiGraph Server sollte dann erscheinen):
[box]ps aux | grep ubigraph[/box]
Ein laufender Server macht sich in der Taskleiste auch mit einem eignen Fensert mit schwarzem (“leeren”) Inhalt bemerkbar. In diesem Fenster werden die Graphen visualisiert.
Wenn der Server läuft, kann in die beliebige Python-IDE gewechselt werden. Dort ein neues Python-Projekt erstellen und als Referenz ubigraph.py einbinden. Diese ist zu finden unter:
[box][ubigraph-Verzeichnis]/examples/Python/ubigraph.py[/box]
Wenn ubigraph.py (bzw. das Verzeichnis, in der diese Datei liegt) in das Python-Projekt eingebunden ist, kann diese API im Projekt wie folgt importiert und beispielhaft verwendet werden:
import ubigraph #Einbinden von UbiGraph :-) U = ubigraph.Ubigraph() U.clear() x = U.newVertex(shape="sphere", color="#32f532", size="1.0", label="Node A") y = U.newVertex(shape="icosahedron", color="#4372f2", size="1.2", label="Node B") z = U.newVertex(shape="torus", color="#ff1010", size="0.8", label="Node C") U.newEdge(x, y, stroke="dashed", strength="1.0") U.newEdge(x, z, stroke="solid", strength="0.8") U.newEdge(y, z, stroke="dotted", strength="1.2", spline="true")
Der obige Beispielcode generiert nach dem Einbinden und Instanziieren von UbiGraph zu erst drei Knoten (Vertexes) mit optionalen Parametern (Form, Farbe, Größe und Beschriftung) und dann drei Kanten, die alle drei Knoten miteinander verschiedenartig verbinden. Das Ergebnis ist in folgender Gif-Datei zu bestaunen: (bevor bzw. während der Ausführung des Python-Skripts muss der UbiGraph-Server aktiv laufen)
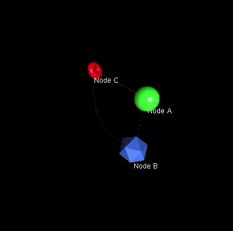
Durch die Visualisierung kann interaktiv in alle Dimensionen navigiert werden.
Dieses Minimalbeispiel sollte bereits ausreichen, um das Prinzip von UbiGraph und die Möglichkeiten damit ausreichend zu erklären. Wir können mit UbiGraph also beliebig aussehende Knoten in einen dreidimensionalen Raum platzieren und beliebig miteinander verbinden. Eine kurze Referenz über die Möglichkeiten findet sich über diesen Link (Klick).
Beispiel – Aufruf von zufälligen Graphen via Rekursion
Folgender Python-Code steigt in der main()-Funktion ein und ruft dann die Methode makeNode() auf, welche einen Knoten anlegt. Für jeden Knoten werden dann nach dem (Pseudo-)Zufallszahlenprinzip eine weitere Menge (0-3) an Unterknoten erzeugt. Um die Menge an Knoten auf 7 pro Ast (ausgehend vom Hauptknoten) zu begrenzen, stoppt der rekursive Aufruf bei einer Knotentiefe von 7.
import ubigraph
from random import randint
U = ubigraph.Ubigraph()
U.clear()
NodeStyle = U.newVertexStyle(shape="sphere", color="#ff0000", size="0.8")
SubNodeStyle = U.newVertexStyle(shape="cube", color="#ff3421", size="0.5")
def main():
makeNode("MainNode", 0, 0) # Aufruf des Hauptknotens (Level = 0)
def makeNode(Name, ParentNode, Level):
if Level > 7:
return # bei einer Tiefe des Knoten-Levels von größer als 7 soll die Rekursion stoppen
current = U.newVertex(label=str(Level))
current.set(color = "#36"+str(Level)+str(Level)+str(Level)+str(Level)) # Unterschiedliche Knotenfarbe je Level
current.set(size=str((10-(Level*1.2))*0.3)) # je tiefer das Level, desto kleiner der Knoten
current.set(shape='sphere')
if ParentNode != 0:
U.newEdge(current, ParentNode)
rand = randint(0,3)
for i in range(0, rand):
makeNode("SubNode" + str(Level), current, Level+1)
main()
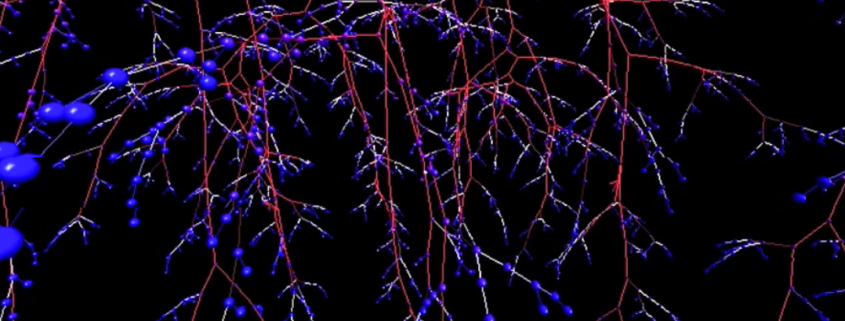
Das Ergebnis ist ein Baum aus miteinander verbundener Knoten. Jeder Knoten ist dabei an einem Ast hängend, der zum Ursprung (Hauptknoten, Level = 0) führt. Da hier mit Pseudo-Zufallszahlen gearbeitet wird, sieht das Ergebnis jedes Mal etwas anders aus, in einigen Fällen bleibt es nur beim Hauptknoten ohne Unterknoten.









Leave a Reply
Want to join the discussion?Feel free to contribute!