Tag Archive for: NLP

Benjamin Aunkofer

Monitoring of Jobskills with Data Engineering & AI

/in , , , , , , , , , , , , /by

On own account, we from DATANOMIQ have created a web application that monitors data about job postings related to Data & AI from multiple sources (Indeed.com, Google Jobs, Stepstone.de and more).

The data is obtained from the Internet via APIs and web scraping, and the job titles and the skills listed in them are identified and extracted from them using Natural Language Processing (NLP) or more specific from Named-Entity Recognition (NER).

The skill clusters are formed via the discipline of Topic Modelling, a method from unsupervised machine learning, which show the differences in the distribution of requirements between them.

The whole web app is hosted and deployed on the Microsoft Azure Cloud via CI/CD and Infrastructure as Code (IaC).

The presentation is currently limited to the current situation on the labor market. However, we collect these over time and will make trends secure, for example how the demand for Python, SQL or specific tools such as dbt or Power BI changes.

Why we did it? It is a nice show-case many people are interested in. Over the time, it will provides you the answer on your questions related to which tool to learn! For DATANOMIQ this is a show-case of the coming Data as a Service (DaaS) Business.

Ram Tavva

Bag of Words: Convert text into vectors

/in , , , , , , /by

In this blog, we will study about the model that represents and converts text to numbers i.e. the Bag of Words (BOW). The bag-of-words model has seen great success in solving problems which includes language modeling and document classification as it is simple to understand and implement.

After completing this particular blog, you all will have an overview of: What does the bag-of-words model mean by and why is its importance in representing text. How we can develop a bag-of-words model for a collection of documents. How to use the bag of words to prepare a vocabulary and deploy in a model using programming language.

 

The problem and its solution…

The biggest problem with modeling text is that it is unorganised, and most of the statistical algorithms, i.e., the machine learning and deep learning techniques prefer well defined numeric data. They cannot work with raw text directly, therefore we have to convert text into numbers.

Word embeddings are commonly used in many Natural Language Processing (NLP) tasks because they are found to be useful representations of words and often lead to better performance in the various tasks performed. A huge number of approaches exist in this regard, among which some of the most widely used are Bag of Words, Fasttext, TF-IDF, Glove and word2vec. For easy user implementation, several libraries exist, such as Scikit-Learn and NLTK, which can implement these techniques in one line of code. But it is important to understand the working principle behind these word embedding techniques. As already said before, in this blog, we see how to implement Bag of words and the best way to do so is to implement these techniques from scratch in Python . Before we start with coding, let’s try to understand the theory behind the model approach.

 Theory Behind Bag of Words Approach

In simple words, Bag of words can be defined as a Natural Language Processing technique used for text modelling or we can say that it is a method of feature extraction with text data from documents.  It involves mainly two things firstly, a vocabulary of known words and, then a measure of the presence of known words.

The process of converting NLP text into numbers is called vectorization in machine learning language.A lot of different ways are available in converting text into vectors which are:

Counting the number of times each word appears in a document, and Calculating the frequency that each word appears in a document out of all the words in the document.

Understanding using an example

To understand the bag of words approach, let’s see how this technique converts text into vectors with the help of an example. Suppose we have a corpus with three sentences:

  1. “I like to eat mangoes”
  2. “Did you like to eat jellies?”
  3. “I don’t like to eat jellies”

Step 1: Firstly, we go through all the words in the above three sentences and make a list of all of the words present in our model vocabulary.

  1. I
  2. like
  3. to
  4. eat
  5. mangoes
  6. Did
  7. you
  8. like
  9. to
  10. eat
  11. Jellies
  12. I
  13. don’t
  14. like
  15. to
  16. eat
  17. jellies

Step 2: Let’s find out the frequency of each word without preprocessing our text.

But is this not the best way to perform a bag of words. In the above example, the words Jellies and jellies are considered twice no doubt they hold the same meaning. So, let us make some changes and see how we can use ‘bag of words’ by preprocessing our text in a more effective way.

Step 3: Let’s find out the frequency of each word with preprocessing our text. Preprocessing is so very important because it brings our text into such a form that is easily understandable, predictable and analyzable for our task.

Firstly, we need to convert the above sentences into lowercase characters as case does not hold any information. Then it is very important to remove any special characters or punctuations if present in our document, or else it makes the conversion more messy.

From the above explanation, we can say the major advantage of Bag of Words is that it is very easy to understand and quite simple to implement in our datasets. But this approach has some disadvantages too such as:

  1. Bag of words leads to a high dimensional feature vector due to the large size of word vocabulary.
  2. Bag of words assumes all words are independent of each other ie’, it doesn’t leverage co-occurrence statistics between words.
  3. It leads to a highly sparse vector as there is nonzero value in dimensions corresponding to words that occur in the sentence.

Bag of Words Model in Python Programming

The first thing that we need to create is a proper dataset for implementing our Bag of Words model. In the above sections, we have manually created a bag of words model with three sentences. However, now we shall find a random corpus on Wikipedia such as ‘https://en.wikipedia.org/wiki/Bag-of-words_model‘.

Step 1: The very first step is to import the required libraries: nltk, numpy, random, string, bs4, urllib.request and re.

Step 2: Once we are done with importing the libraries, now we will be using the Beautifulsoup4 library to parse the data from Wikipedia.Along with that we shall be using Python’s regex library, re, for preprocessing tasks of our document. So, we will scrape the Wikipedia article on Bag of Words.

Step 3: As we can observe, in the above code snippet we have imported the raw HTML for the Wikipedia article from which we have filtered the text within the paragraph text and, finally,have created a complete corpus by merging up all the paragraphs.

Step 4: The very next step is to split the corpus into individual sentences by using the sent_tokenize function from the NLTK library.

Step 5: Our text contains a number of punctuations which are unnecessary for our word frequency dictionary. In the below code snippet, we will see how to convert our text into lower case and then remove all the punctuations from our text, which will result in multiple empty spaces which can be again removed using regex.

Step 6: Once the preprocessing is done, let’s find out the number of sentences present in our corpus and then, print one sentence from our corpus to see how it looks.

Step 7: We can observe that the text doesn’t contain any special character or multiple empty spaces, and so our own corpus is ready. The next step is to tokenize each sentence in the corpus and create a dictionary containing each word and their corresponding frequencies.

As you can see above, we have created a dictionary called wordfreq. Next, we iterate through each word in the sentence and check if it exists in the wordfreq dictionary.  On its existence,we will add the word as the key and set the value of the word as 1.

Step 8: Our corpus has more than 500 words in total and so we shall filter down to the 200 most frequently occurring words by using Python’s heap library.


Step 9: Now, comes the final step of converting the sentences in our corpus into their corresponding vector representation. Let’s check the below code snippet to understand it. Our model is in the form of a list of lists which can be easily converted matrix form using this script:

Yasuto Tamura

Multi-head attention mechanism: “queries”, “keys”, and “values,” over and over again

/in , , , , , , , , , , /by

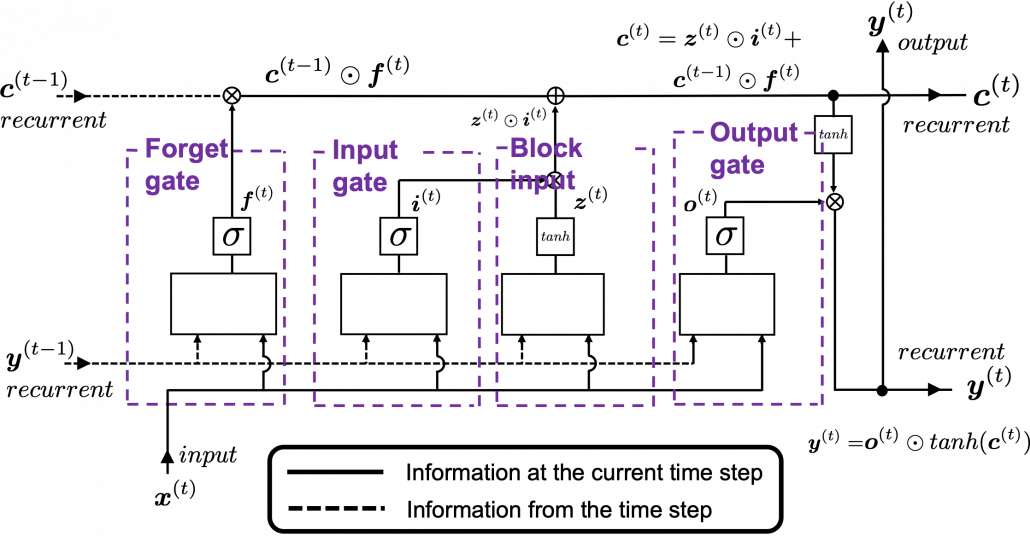
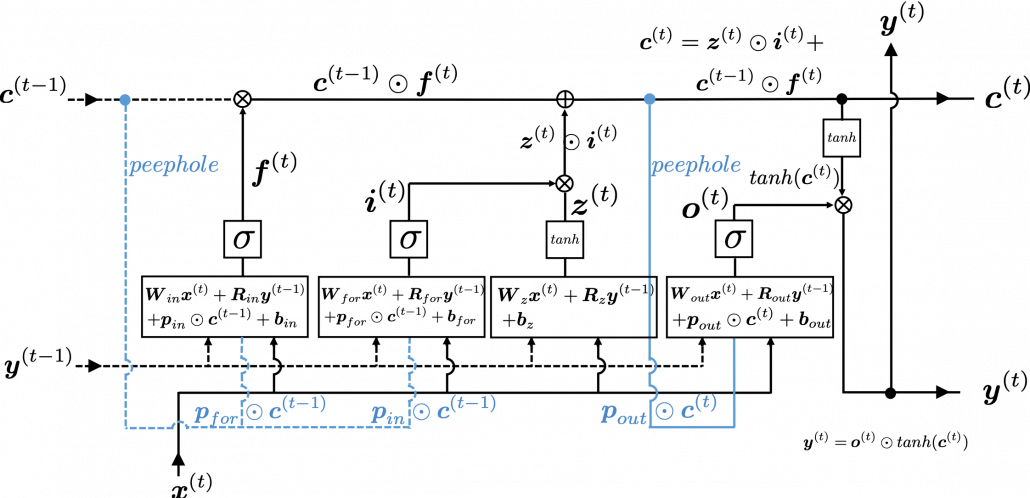
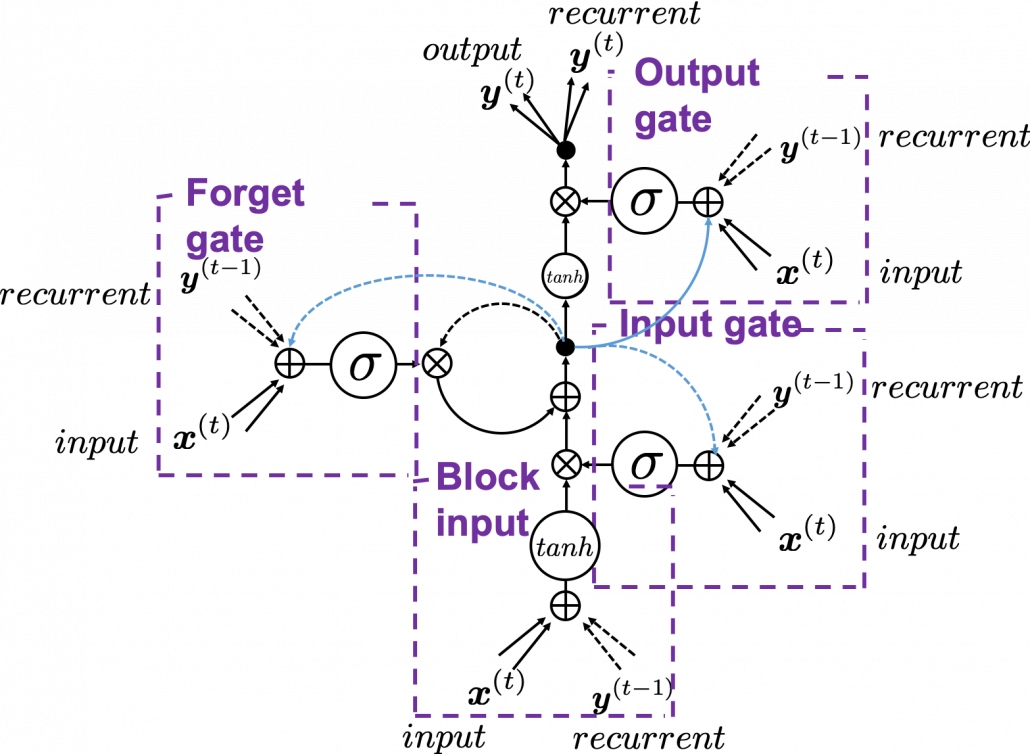
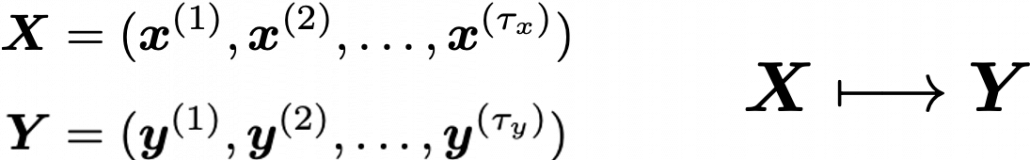This is the third article of my article series named “Instructions on Transformer for people outside NLP field, but with examples of NLP.”

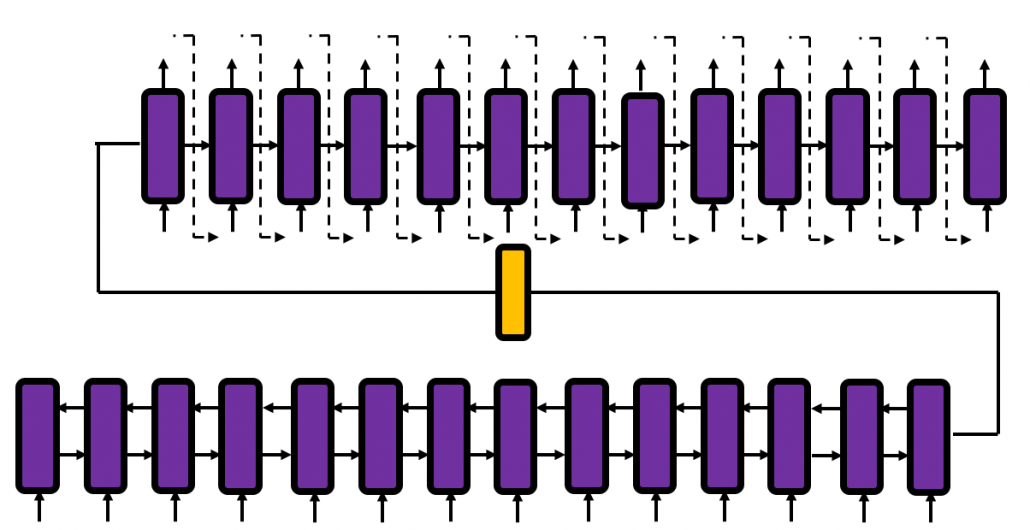
In the last article, I explained how attention mechanism works in simple seq2seq models with RNNs, and it basically calculates correspondences of the hidden state at every time step, with all the outputs of the encoder. However I would say the attention mechanisms of RNN seq2seq models use only one standard for comparing them. Using only one standard is not enough for understanding languages, especially when you learn a foreign language. You would sometimes find it difficult to explain how to translate a word in your language to another language. Even if a pair of languages are very similar to each other, translating them cannot be simple switching of vocabulary. Usually a single token in one language is related to several tokens in the other language, and vice versa. How they correspond to each other depends on several criteria, for example “what”, “who”, “when”, “where”, “why”, and “how”. It is easy to imagine that you should compare tokens with several criteria.

Transformer model was first introduced in the original paper named “Attention Is All You Need,” and from the title you can easily see that attention mechanism plays important roles in this model. When you learn about Transformer model, you will see the figure below, which is used in the original paper on Transformer.  This is the simplified overall structure of one layer of Transformer model, and you stack this layer N times. In one layer of Transformer, there are three multi-head attention, which are displayed as boxes in orange. These are the very parts which compare the tokens on several standards. I made the head article of this article series inspired by this multi-head attention mechanism.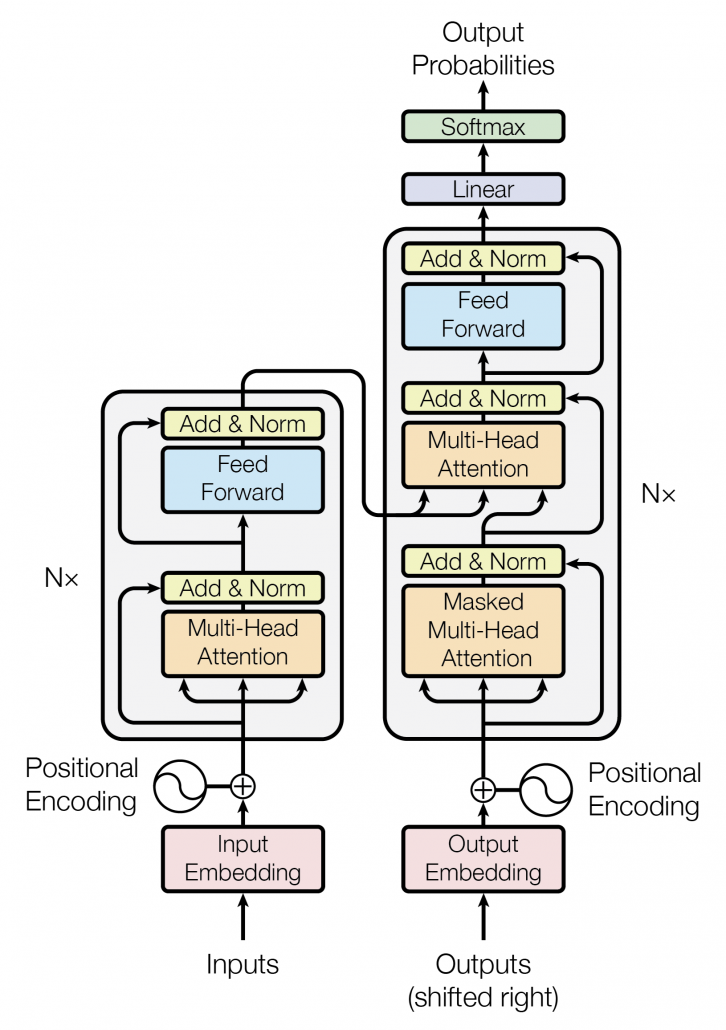

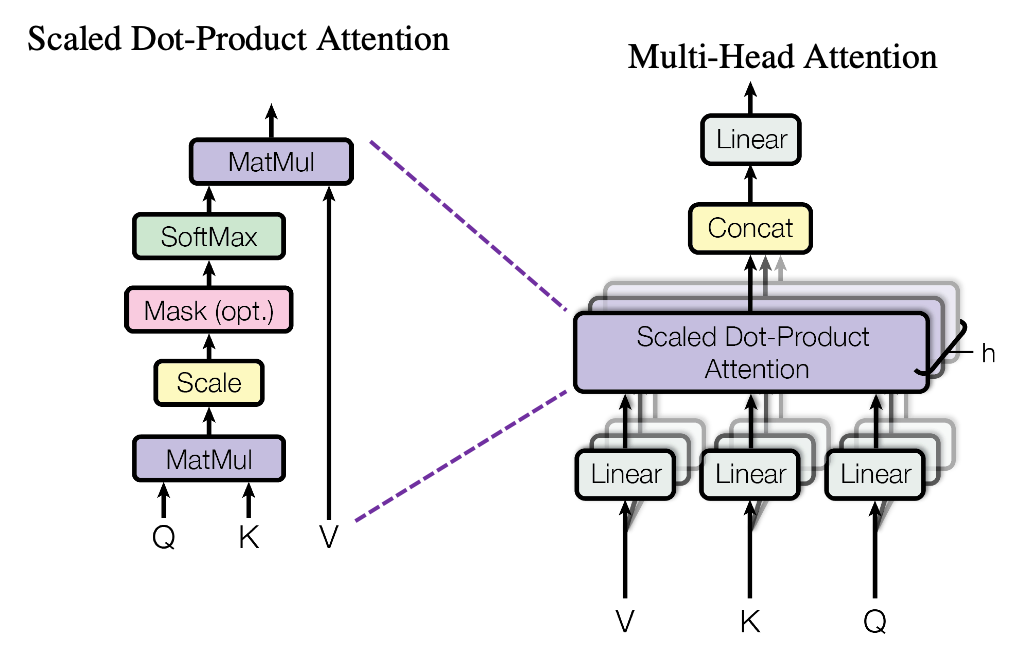
The figure below is also from the original paper on Transfromer. If you can understand how multi-head attention mechanism works with the explanations in the paper, and if you have no troubles understanding the codes in the official Tensorflow tutorial, I have to say this article is not for you. However I bet that is not true of majority of people, and at least I need one article to clearly explain how multi-head attention works. Please keep it in mind that this article covers only the architectures of the two figures below. However multi-head attention mechanisms are crucial components of Transformer model, and throughout this article, you would not only see how they work but also get a little control over it at an implementation level.

1 Multi-head attention mechanism

When you learn Transformer model, I recommend you first to pay attention to multi-head attention. And when you learn multi-head attentions, before seeing what scaled dot-product attention is, you should understand the whole structure of multi-head attention, which is at the right side of the figure above. In order to calculate attentions with a “query”, as I said in the last article, “you compare the ‘query’ with the ‘keys’ and get scores/weights for the ‘values.’ Each score/weight is in short the relevance between the ‘query’ and each ‘key’. And you reweight the ‘values’ with the scores/weights, and take the summation of the reweighted ‘values’.” Sooner or later, you will notice I would be just repeating these phrases over and over again throughout this article, in several ways.

*Even if you are not sure what “reweighting” means in this context, please keep reading. I think you would little by little see what it means especially in the next section.

The overall process of calculating multi-head attention, displayed in the figure above, is as follows (Please just keep reading. Please do not think too much.): first you split the V: “values”, K: “keys”, and Q: “queries”, and second you transform those divided “values”, “keys”, and “queries” with densely connected layers (“Linear” in the figure). Next you calculate attention weights and reweight the “values” and take the summation of the reiweighted “values”, and you concatenate the resulting summations. At the end you pass the concatenated “values” through another densely connected layers. The mechanism of scaled dot-product attention is just a matter of how to concretely calculate those attentions and reweight the “values”.

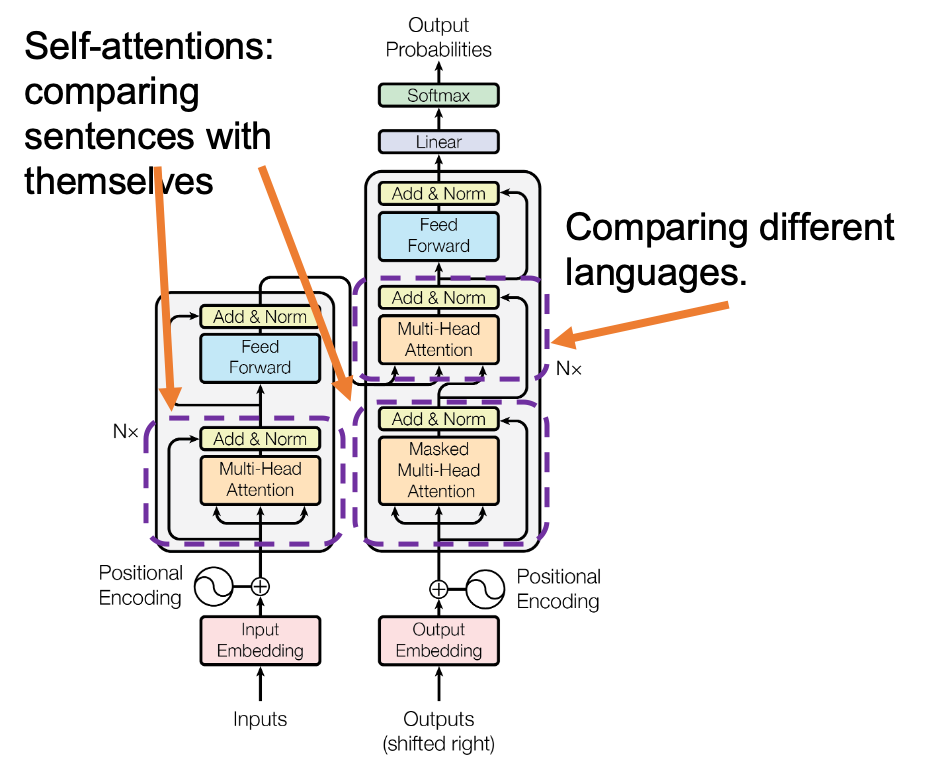
*In the last article I briefly mentioned that “keys” and “queries” can be in the same language. They can even be the same sentence in the same language, and in this case the resulting attentions are called self-attentions, which we are mainly going to see. I think most people calculate “self-attentions” unconsciously when they speak. You constantly care about what “she”, “it” , “the”, or “that” refers to in you own sentence, and we can say self-attention is how these everyday processes is implemented.

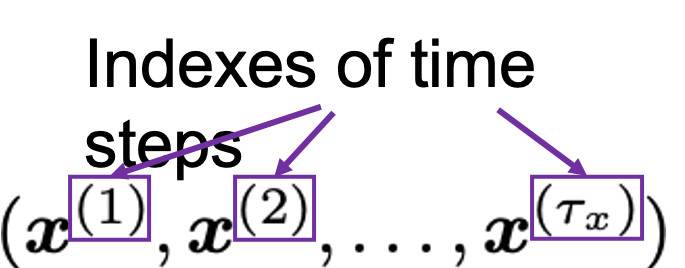
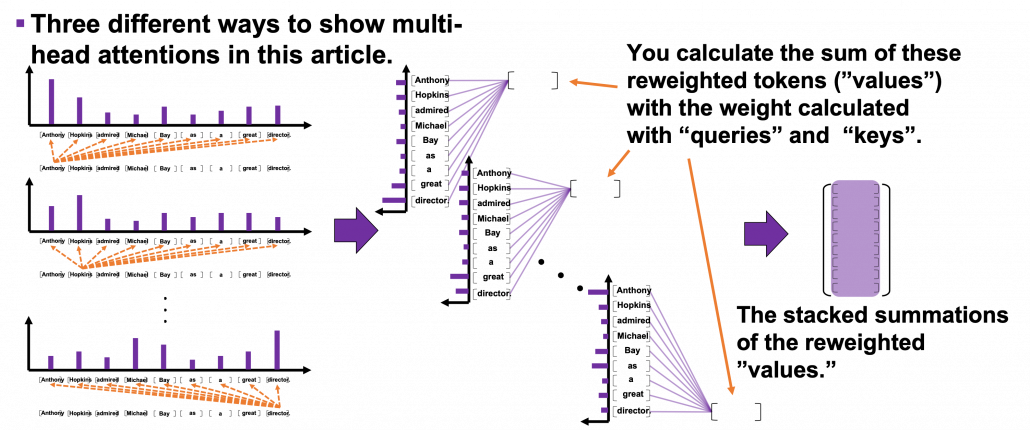
Let’s see the whole process of calculating multi-head attention at a little abstract level. From now on, we consider an example of calculating multi-head self-attentions, where the input is a sentence “Anthony Hopkins admired Michael Bay as a great director.” In this example, the number of tokens is 9, and each token is encoded as a 512-dimensional embedding vector. And the number of heads is 8. In this case, as you can see in the figure below, the input sentence “Anthony Hopkins admired Michael Bay as a great director.” is implemented as a 9\times 512 matrix. You first split each token into 512/8=64 dimensional, 8 vectors in total, as I colored in the figure below. 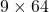In other words, the input matrix is divided into 8 colored chunks, which are all 9\times 64 matrices, but each colored matrix expresses the same sentence. And you calculate self-attentions of the input sentence independently in the 8 heads, and you reweight the “values” according to the attentions/weights. After this, you stack the sum of the reweighted “values”  in each colored head, and you concatenate the stacked tokens of each colored head. The size of each colored chunk does not change even after reweighting the tokens. According to Ashish Vaswani, who invented Transformer model, each head compare “queries” and “keys” on each standard. If the a Transformer model has 4 layers with 8-head multi-head attention , at least its encoder has 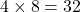4\times 8 = 32 heads, so the encoder learn the relations of tokens of the input on 32 different standards.

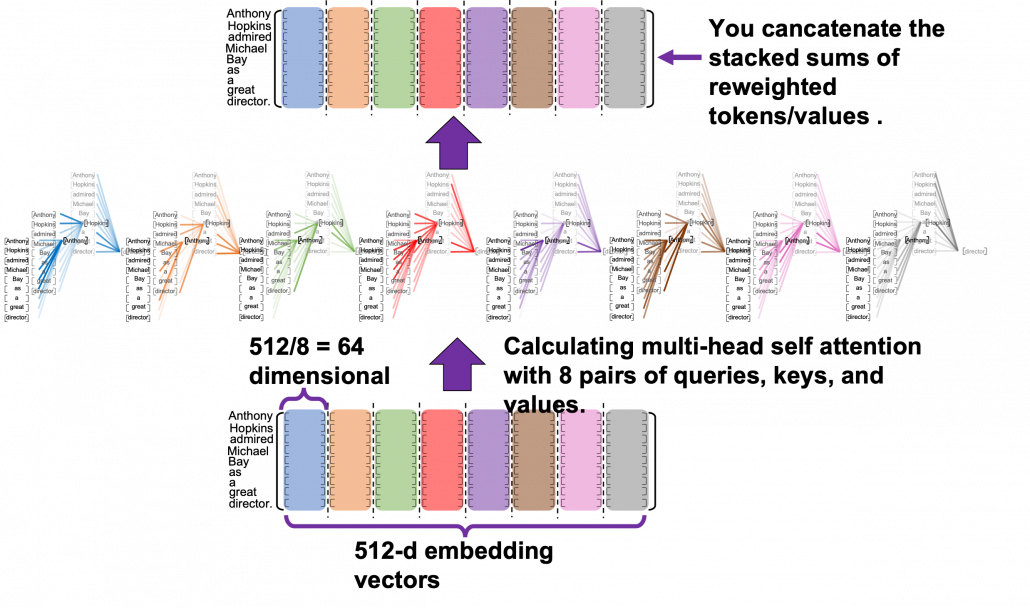
I think you now have rough insight into how you calculate multi-head attentions. In the next section I am going to explain the process of reweighting the tokens, that is, I am finally going to explain what those colorful lines in the head image of this article series are.

*Each head is randomly initialized, so they learn to compare tokens with different criteria. The standards might be straightforward like “what” or “who”, or maybe much more complicated. In attention mechanisms in deep learning, you do not need feature engineering for setting such standards.

2 Calculating attentions and reweighting “values”

If you have read the last article or if you understand attention mechanism to some extent, you should already know that attention mechanism calculates attentions, or relevance between “queries” and “keys.” In the last article, I showed the idea of weights as a histogram, and in that case the “query” was the hidden state of the decoder at every time step, whereas the “keys” were the outputs of the encoder. In this section, I am going to explain attention mechanism in a more abstract way, and we consider comparing more general “tokens”, rather than concrete outputs of certain networks. In this section each [ \cdots ] denotes a token, which is usually an embedding vector in practice.

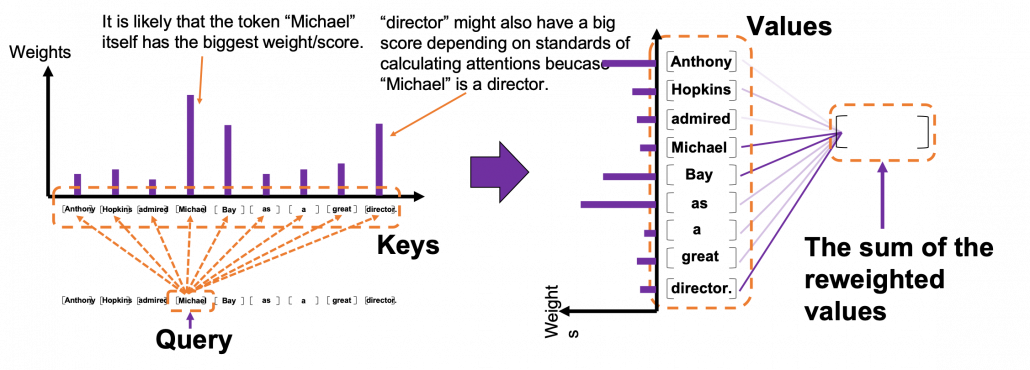
Please remember this mantra of attention mechanism: “you compare the ‘query’ with the ‘keys’ and get scores/weights for the ‘values.’ Each score/weight is in short the relevance between the ‘query’ and each ‘key’. And you reweight the ‘values’ with the scores/weights, and take the summation of the reweighted ‘values’.” The figure below shows an overview of a case where “Michael” is a query. In this case you compare the query with the “keys”, that is, the input sentence “Anthony Hopkins admired Michael Bay as a great director.” and you get the histogram of attentions/weights. Importantly the sum of the weights 1. With the attentions you have just calculated, you can reweight the “values,” which also denote the same input sentence. After that you can finally take a summation of the reweighted values. And you use this summation.

*I have been repeating the phrase “reweighting ‘values’  with attentions,”  but you in practice calculate the sum of those reweighted “values.”

Assume that compared to the “query”  token “Michael”, the weights of the “key” tokens “Anthony”, “Hopkins”, “admired”, “Michael”, “Bay”, “as”, “a”, “great”, and “director.” are respectively 0.06, 0.09, 0.05, 0.25, 0.18, 0.06, 0.09, 0.06, 0.15. In this case the sum of the reweighted token is 0.06″Anthony” + 0.09″Hopkins” + 0.05″admired” + 0.25″Michael” + 0.18″Bay” + 0.06″as” + 0.09″a” + 0.06″great” 0.15″director.”, and this sum is the what wee actually use.

*Of course the tokens are embedding vectors in practice. You calculate the reweighted vector in actual implementation.

You repeat this process for all the “queries.”  As you can see in the figure below, you get summations of 9 pairs of reweighted “values” because you use every token of the input sentence “Anthony Hopkins admired Michael Bay as a great director.” as a “query.” You stack the sum of reweighted “values” like the matrix in purple in the figure below, and this is the output of a one head multi-head attention.

3 Scaled-dot product

This section is a only a matter of linear algebra. Maybe this is not even so sophisticated as linear algebra. You just have to do lots of Excel-like operations. A tutorial on Transformer by Jay Alammar is also a very nice study material to understand this topic with simpler examples. I tried my best so that you can clearly understand multi-head attention at a more mathematical level, and all you need to know in order to read this section is how to calculate products of matrices or vectors, which you would see in the first some pages of textbooks on linear algebra.

We have seen that in order to calculate multi-head attentions, we prepare 8 pairs of “queries”, “keys” , and “values”, which I showed in 8 different colors in the figure in the first section. We calculate attentions and reweight “values” independently in 8 different heads, and in each head the reweighted “values” are calculated with this very simple formula of scaled dot-product: 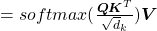Attention(\boldsymbol{Q}, \boldsymbol{K}, \boldsymbol{V}) =softmax(\frac{\boldsymbol{Q} \boldsymbol{K} ^T}{\sqrt{d}_k})\boldsymbol{V}. Let’s take an example of calculating a scaled dot-product in the blue head.

At the left side of the figure below is a figure from the original paper on Transformer, which explains one-head of multi-head attention. If you have read through this article so far, the figure at the right side would be more straightforward to understand. You divide the input sentence into 8 chunks of matrices, and you independently put those chunks into eight head. In one head, you convert the input matrix by three different fully connected layers, which is “Linear” in the figure below, and prepare three matrices 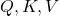Q, K, V, which are “queries”, “keys”, and “values” respectively.

*Whichever color attention heads are in, the processes are all the same.

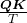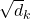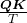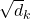*You divide \frac{\boldsymbol{Q} \boldsymbol{K}} ^T by \sqrt{d}_k in the formula. According to the original paper, it is known that re-scaling \frac{\boldsymbol{Q} \boldsymbol{K}} ^T by \sqrt{d}_k is found to be effective. I am not going to discuss why in this article.

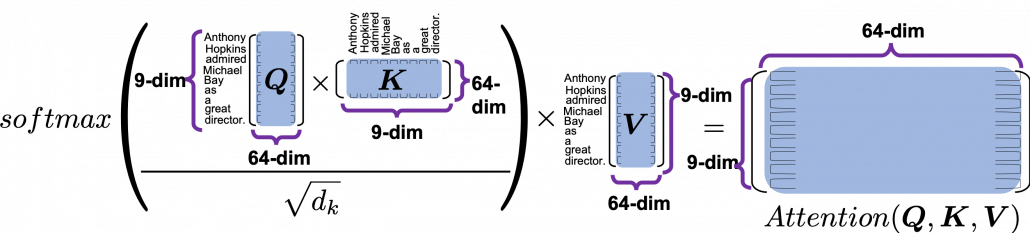
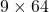As you can see in the figure below, calculating Attention(\boldsymbol{Q}, \boldsymbol{K}, \boldsymbol{V}) is virtually just multiplying three matrices with the same size (Only K is transposed though). The resulting 9\times 64 matrix is the output of the head.

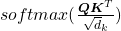softmax(\frac{\boldsymbol{Q} \boldsymbol{K} ^T}{\sqrt{d}_k}) is calculated like in the figure below. The softmax function regularize each row of the re-scaled product 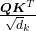\frac{\boldsymbol{Q} \boldsymbol{K} ^T}{\sqrt{d}_k}, and the resulting 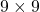9\times 9 matrix is a kind a heat map of self-attentions.

The process of comparing one “query” with “keys” is done with simple multiplication of a vector and a matrix, as you can see in the figure below. You can get a histogram of attentions for each query, and the resulting 9 dimensional vector is a list of attentions/weights, which is a list of blue circles in the figure below. That means, in Transformer model, you can compare a “query” and a “key” only by calculating an inner product. After re-scaling the vectors by dividing them with 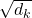\sqrt{d_k} and regularizing them with a softmax function, you stack those vectors, and the stacked vectors is the heat map of attentions.

You can reweight “values” with the heat map of self-attentions, with simple multiplication. It would be more straightforward if you consider a transposed scaled dot-product 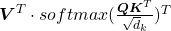\boldsymbol{V}^T \cdot softmax(\frac{\boldsymbol{Q} \boldsymbol{K} ^T}{\sqrt{d}_k})^T. This also should be easy to understand if you know basics of linear algebra.

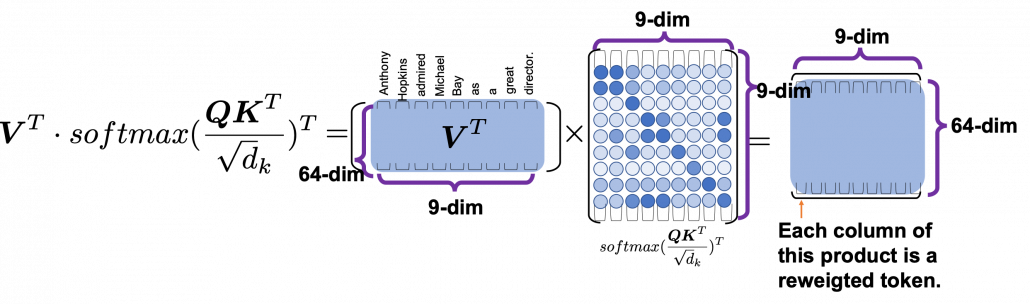
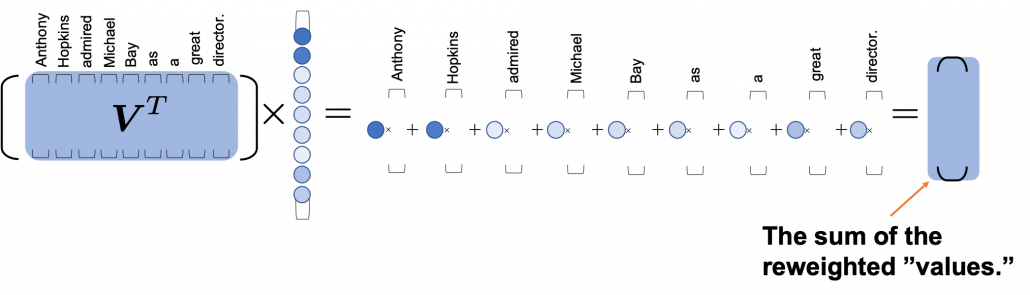
One column of the resulting matrix (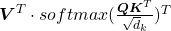\boldsymbol{V}^T \cdot softmax(\frac{\boldsymbol{Q} \boldsymbol{K} ^T}{\sqrt{d}_k})^T) can be calculated with a simple multiplication of a matrix and a vector, as you can see in the figure below. This corresponds to the process or “taking a summation of reweighted ‘values’,” which I have been repeating. And I would like you to remember that you got those weights (blue) circles by comparing a “query” with “keys.”

Again and again, let’s repeat the mantra of attention mechanism together: “you compare the ‘query’ with the ‘keys’ and get scores/weights for the ‘values.’ Each score/weight is in short the relevance between the ‘query’ and each ‘key’. And you reweight the ‘values’ with the scores/weights, and take the summation of the reweighted ‘values’.” If you have been patient enough to follow my explanations, I bet you have got a clear view on how multi-head attention mechanism works.

We have been seeing the case of the blue head, but you can do exactly the same procedures in every head, at the same time, and this is what enables parallelization of multi-head attention mechanism. You concatenate the outputs of all the heads, and you put the concatenated matrix through a fully connected layers.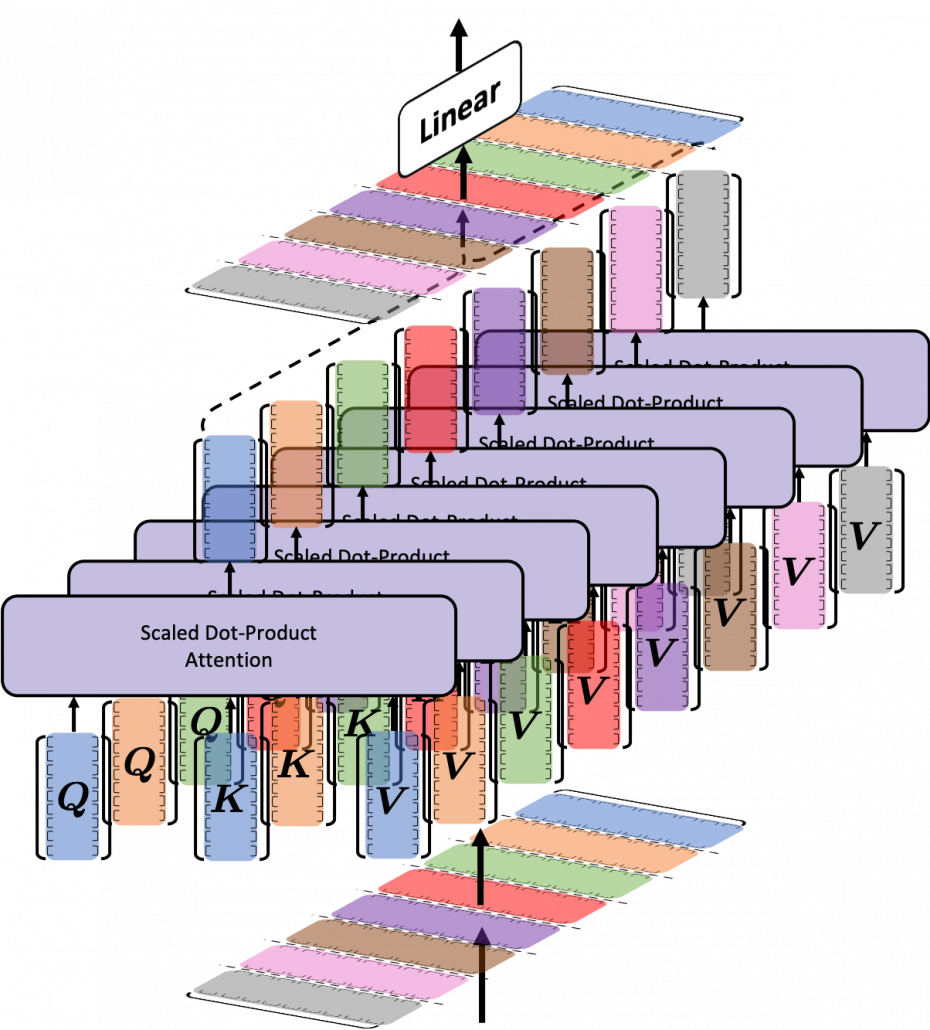

If you are reading this article from the beginning, I think this section is also showing the same idea which I have repeated, and I bet more or less you no have clearer views on how multi-head attention mechanism works. In the next section we are going to see how this is implemented.

4 Tensorflow implementation of multi-head attention

Let’s see how multi-head attention is implemented in the Tensorflow official tutorial. If you have read through this article so far, this should not be so difficult. I also added codes for displaying heat maps of self attentions. With the codes in this Github page, you can display self-attention heat maps for any input sentences in English.

The multi-head attention mechanism is implemented as below. If you understand Python codes and Tensorflow to some extent, I think this part is relatively easy.  The multi-head attention part is implemented as a class because you need to train weights of some fully connected layers. Whereas, scaled dot-product is just a function.

*I am going to explain the create_padding_mask() and create_look_ahead_mask() functions in upcoming articles. You do not need them this time.

Let’s see a case of using multi-head attention mechanism on a (1, 9, 512) sized input tensor, just as we have been considering in throughout this article. The first axis of (1, 9, 512) corresponds to the batch size, so this tensor is virtually a (9, 512) sized tensor, and this means the input is composed of 9 512-dimensional vectors. In the results below, you can see how the shape of input tensor changes after each procedure of calculating multi-head attention. Also you can see that the output of the multi-head attention is the same as the input, and you get a 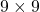9\times 9 matrix of attention heat maps of each attention head.

I guess the most complicated part of this implementation above is the split_head() function, especially if you do not understand tensor arithmetic. This part corresponds to splitting the input tensor to 8 different colored matrices as in one of the figures above. If you cannot understand what is going on in the function, I recommend you to prepare a sample tensor as below.

This is just a simple (1, 9, 512) sized tensor with sequential integer elements. The first row (1, 2, …., 512) corresponds to the first input token, and (4097, 4098, … , 4608) to the last one. You should try converting this sample tensor to see how multi-head attention is implemented. For example you can try the operations below.

These operations correspond to splitting the input into 8 heads, whose sizes are all (9, 64). And the second axis of the resulting (1, 8, 9, 64) tensor corresponds to the index of the heads. Thus sample_sentence[0][0] corresponds to the first head, the blue 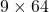9\times 64 matrix. Some Tensorflow functions enable linear calculations in each attention head, independently as in the codes below.

Very importantly, we have been only considering the cases of calculating self attentions, where all “queries”, “keys”, and “values” come from the same sentence in the same language. However, as I showed in the last article, usually “queries” are in a different language from “keys” and “values” in translation tasks, and “keys” and “values” are in the same language. And as you can imagine, usualy “queries” have different number of tokens from “keys” or “values.” You also need to understand this case, which is not calculating self-attentions. If you have followed this article so far, this case is not that hard to you. Let’s briefly see an example where the input sentence in the source language is composed 9 tokens, on the other hand the output is composed 12 tokens.

As I mentioned, one of the outputs of each multi-head attention class is 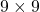9\times 9 matrix of attention heat maps, which I displayed as a matrix composed of blue circles in the last section. The the implementation in the Tensorflow official tutorial, I have added codes to display actual heat maps of any input sentences in English.

*If you want to try displaying them by yourself, download or just copy and paste codes in this Github page. Please maker “datasets” directory in the same directory as the code. Please download “spa-eng.zip” from this page, and unzip it. After that please put “spa.txt” on the “datasets” directory. Also, please download the “checkpoints_en_es” folder from this link, and place the folder in the same directory as the file in the Github page. In the upcoming articles, you would need similar processes to run my codes.

After running codes in the Github page, you can display heat maps of self attentions. Let’s input the sentence “Anthony Hopkins admired Michael Bay as a great director.” You would get a heat maps like this.

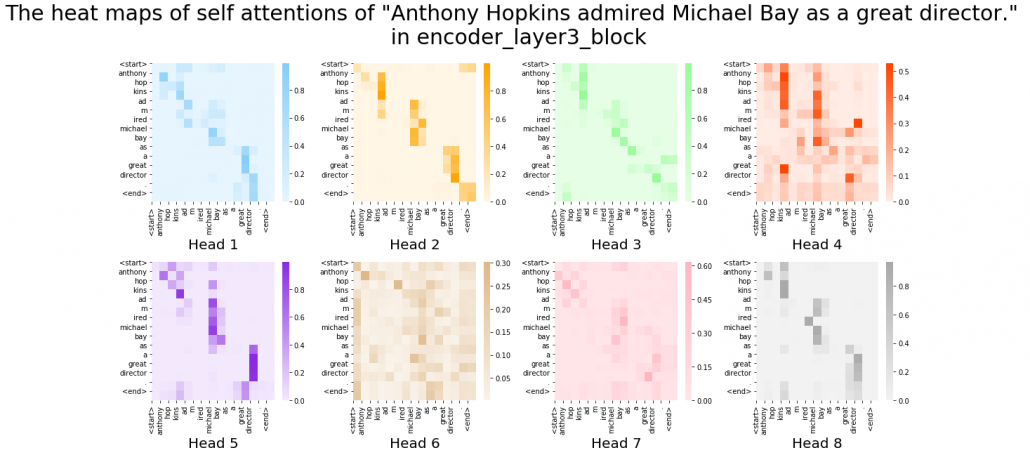
In fact, my toy implementation cannot handle proper nouns such as “Anthony” or “Michael.” Then let’s consider a simple input sentence “He admired her as a great director.” In each layer, you respectively get 8 self-attention heat maps.

I think we can see some tendencies in those heat maps. The heat maps in the early layers, which are close to the input, are blurry. And the distributions of the heat maps come to concentrate more or less diagonally. At the end, presumably they learn to pay attention to the start and the end of sentences.

You have finally finished reading this article. Congratulations.

You should be proud of having been patient, and you passed the most tiresome part of learning Transformer model. You must be ready for making a toy English-German translator in the upcoming articles. Also I am sure you have understood that Michael Bay is a great director, no matter what people say.

*Hannibal Lecter, I mean Athony Hopkins, also wrote a letter to the staff of “Breaking Bad,” and he told them the tv show let him regain his passion. He is a kind of admiring around, and I am a little worried that he might be getting senile. He played a role of a father forgetting his daughter in his new film “The Father.” I must see it to check if that is really an acting, or not.

[References]

[1] Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N. Gomez, Lukasz Kaiser, Illia Polosukhin, “Attention Is All You Need” (2017)

[2] “Transformer model for language understanding,” Tensorflow Core
https://www.tensorflow.org/overview

[3] “Neural machine translation with attention,” Tensorflow Core
https://www.tensorflow.org/tutorials/text/nmt_with_attention

[4] Jay Alammar, “The Illustrated Transformer,”
http://jalammar.github.io/illustrated-transformer/

[5] “Stanford CS224N: NLP with Deep Learning | Winter 2019 | Lecture 14 – Transformers and Self-Attention,” stanfordonline, (2019)
https://www.youtube.com/watch?v=5vcj8kSwBCY

[6]Tsuboi Yuuta, Unno Yuuya, Suzuki Jun, “Machine Learning Professional Series: Natural Language Processing with Deep Learning,” (2017), pp. 91-94
坪井祐太、海野裕也、鈴木潤 著, 「機械学習プロフェッショナルシリーズ 深層学習による自然言語処理」, (2017), pp. 191-193

[7]”Stanford CS224N: NLP with Deep Learning | Winter 2019 | Lecture 8 – Translation, Seq2Seq, Attention”, stanfordonline, (2019)
https://www.youtube.com/watch?v=XXtpJxZBa2c

[8]Rosemary Rossi, “Anthony Hopkins Compares ‘Genius’ Michael Bay to Spielberg, Scorsese,” yahoo! entertainment, (2017)
https://www.yahoo.com/entertainment/anthony-hopkins-transformers-director-michael-bay-guy-genius-010058439.html

* I make study materials on machine learning, sponsored by DATANOMIQ. I do my best to make my content as straightforward but as precise as possible. I include all of my reference sources. If you notice any mistakes in my materials, including grammatical errors, please let me know (email: yasuto.tamura@datanomiq.de). And if you have any advice for making my materials more understandable to learners, I would appreciate hearing it.

Support Vector Machines for Text Recognition
Mohan Rai

Hand Written Alphabet recognition Using Support Vector Machine

/in , , , , , /by

We have used image classification as an task in many cases, more often this has been done using an module like openCV in python or using pre-trained models like in case of MNIST data sets. The idea of using Support Vector Machines for carrying out the same task is to give a simpler approach for a complicated process. There are some pro’s and con’s in every algorithm. Support vector machine for data with very high dimension may prove counter productive. But in case of image data we are actually using a array. If its a mono chrome then its just a 2 dimensional array, if grey scale or color image stack then we may have a 3 dimensional array processing to be considered. You can get more clarity on the array part if you go through this article on Machine learning using only numpy array. While there are certainly advantages of using OCR packages like Tesseract or OpenCV or GPTs, I am putting forth this approach of using a simple SVM model for hand written text classification. As a student while doing linear regression, I learn’t a principle “Occam’s Razor”, Basically means, keep things simple if they can explain what you want to. In short, the law of parsimony, simplify and not complicate. Applying the same principle on Hand written Alphabet recognition is an attempt to simplify using a classic algorithm, the Support Vector Machine. We break the  problem of hand written alphabet recognition into a simple process rather avoiding usage of heavy packages. This is an attempt to create the data and then build a model using Support Vector Machines for Classification.

Data Preparation

Manually edit the data instead of downloading it from the web. This will help you understand your data from the beginning. Manually write some letters on white paper and get the photo from your mobile phone. Then store it on your hard drive. As we are doing a trial we don’t want to waste a lot of time in data creation at this stage, so it’s a good idea to create two or three different characters for your dry run. You may need to change the code as you add more instances of classes, but this is where the learning phase begins. We are now at the training level.

Data Structure

You can create the data yourself by taking standard pictures of hand written text in a 200 x 200 pixel dimension. Alternatively you can use a pen tab to manually write these alphabets and save them as files. If you know and photo editing tools you can use them as well. For ease of use, I have already created a sample data and saved it in the structure as below.

Image Source : From Author

You can download the data which I have used, right click on this download data link and open in new tab or window. Then unzip the folders and you should be able to see the same structure and data as above in your downloads folder. I would suggest, you should create your own data and repeat the  process. This would help you understand the complete flow.

Install the Dependency Packages for RStudio

We will be using the jpeg package in R for Image handling and the SVM implementation from the kernlab package.  Also we need to make sure that the image data has dimension’s of 200 x 200 pixels, with a horizontal and vertical resolution of 120dpi. You can vary the dimension’s like move it to 300 x 300 or reduce it to 100 x 100. The higher the dimension, you will need more compute power. Experiment around the color channels and resolution later once you have implemented it in the current form.

# install package "jpeg"

  install.packages("jpeg", dependencies = TRUE)

 

# install the "kernlab" package for building the model using support vector machines

install.packages("kernlab", dependencies  = TRUE)

Load the training data set

# load the "jpeg" package for reading the JPEG format files
library(jpeg)

# set the working directory for reading the training image data set
setwd("C:/Users/mohan/Desktop/alphabet_folder/Train")

# extract the directory names for using as image labels

f_train<-list.files()
 

# Create an empty data frame to store the image data labels and the extracted new features in training environment

df_train<- data.frame(matrix(nrow=0,ncol=5))

Feature Transformation

Since we don’t intend to use the typical CNN, we are going to use the white, grey and black pixel values for new feature creation. We will use the summation of all the pixel values of a image  and save it as a new feature called as “sum”, the count of all pixels adding up to zero as “zero”, the count of all pixels adding up to “ones” and the sum of all pixels between zero’s and one’s as “in_between”. The “label” feature names are extracted from the names of the folder

# names the columns of the data frame as per the feature name schema

names(df_train)<- c("sum","zero","one","in_between","label")

# loop to compute as per the logic

counter<-1 

for(i in 1:length(f_train))

{

setwd(paste("C:/Users/mohan/Desktop/alphabet_folder/Train/",f_train[i],sep=""))

 

data_list<-list.files()

 

  for(j in 1:length(data_list))

  {

    temp<- readJPEG(data_list[j])

    df_train[counter,1]<- sum(temp)

    df_train[counter,2]<- sum(temp==0)

    df_train[counter,3]<- sum(temp==1)

    df_train[counter,4]<- sum(temp > 0 & temp < 1)

    df_train[counter,5]<- f_train[i]

    counter=counter+1

  }

}


# Convert the labels from text to factor form

df_train$label<- factor(df_train$label)

Support Vector Machine model

# load the "kernlab" package for accessing the support vector machine implementation

library(kernlab)


# build the model using the training data

image_classifier <- ksvm(label~.,data=df_train)

Evaluate the Model on the Testing Data Set

# set the working directory for reading the testing image data set

setwd("C:/Users/mohan/Desktop/alphabet_folder/Test")


# extract the directory names for using as image labels

f_test <- list.files()

 
# Create an empty data frame to store the image data labels and the extracted new features in training environment

df_test<- data.frame(matrix(nrow=0,ncol=5))

 
# Repeat of feature extraction in test data

names(df_test)<- c("sum","zero","one","in_between","label")

 
# loop to compute as per the logic

for(i in 1:length(f_test))

{

temp<- readJPEG(f_test[i])

df_test[i,1]<- sum(temp)

df_test[i,2]<- sum(temp==0)

df_test[i,3]<- sum(temp==1)

df_train[counter,4]<- sum(temp > 0 & temp < 1)

df_test[i,5]<- strsplit(x = f_test[i],split = "[.]")[[1]][1]

}
 

# Use the classifier named "image_classifier" built in train environment to predict the outcomes on features in Test environment

df_test$label_predicted<- predict(image_classifier,df_test)
 

# Cross Tab for Classification Metric evaluation

table(Actual_data=df_test$label,Predicted_data=df_test$label_predicted) 

I would recommend you to learn concepts of SVM which couldn’t be explained completely in this article by going through my free Data Science and Machine Learning video courses. We have created the classifier using the Kerlab package in R, but I would advise you to study the mathematics involved in Support vector machines to get a clear understanding.

Yasuto Tamura

On the difficulty of language: prerequisites for NLP with deep learning

/in , , , , , , , , , , , /by

1 Preface

This section is virtually just my essay on language. You can skip this if you want to get down on more technical topic.

As I do not study in natural language processing (NLP) field, I would not be able to provide that deep insight into this fast changing deep leaning field throughout my article series. However at least I do understand language is a difficult and profound field, not only in engineering but also in many other study fields. Some people might be feeling that technologies are eliminating languages, or one’s motivations to understand other cultures. First of all, I would like you to keep it in mind that I am not a geek who is trying to turn this multilingual world into a homogeneous one and rebuild Tower of Babel, with deep learning. I would say I am more keen on social or anthropological sides of language.

I think you would think more about languages if you have mastered at least one foreign language. As my mother tongue is Japanese, which is totally different from many other Western languages in terms of characters and ambiguity, I understand translating is not what learning a language is all about. Each language has unique characteristics, and I believe they more or less influence one’s personalities. For example, many Western languages make the verb, I mean the conclusion, of sentences clear in the beginning part of the sentences. That is also true of Chinese, I heard. However in Japanese, the conclusion comes at the end, so that is likely to give an impression that Japanese people are being obscure or indecisive. Also, Japanese sentences usually omit their subjects. In German as well, the conclusion of a sentences tend to come at the end, but I am almost 100% sure that no Japanese people would feel German people make things unclear. I think that comes from the structures of German language, which tends to make the number, verb, relations of words crystal clear.

Let’s take an example to see how obscure Japanese is. A Japanese sentence 「頭が赤い魚を食べる猫」can be interpreted in five ways, depending on where you put emphases on.

Common sense tells you that the sentence is likely to mean the first two cases, but I am sure they can mean those five possibilities. There might be similarly obscure sentences in other languages, but I bet few languages can be as obscure as Japanese. Also as you can see from the last two sentences, you can omit subjects in Japanese. This rule is nothing exceptional. Japanese people usually don’t use subjects in normal conversations. And when you read classical Japanese, which Japanese high school students have to do just like Western students learn some of classical Latin, the writings omit subjects much more frequently.

*However interestingly we have rich vocabulary of subjects. The subject “I” can be translated to 「私」、「僕」、「俺」、「自分」、「うち」etc, depending on your personality, who you are talking to, and the time when it is written in.

I believe one can see the world only in the framework of their language, and it seems one’s personality changes depending on the language they use. I am not sure whether the language originally determines how they think, or how they think forms the language. But at least I would like you to keep it in mind that if you translate a conversation, for example a random conversation at a bar in Berlin, into Japanese, that would linguistically sound Japanese, but not anthropologically. Imagine that such kind of random conversation in Berlin or something is like playing a catch, I mean throwing a ball named “your opinion.” On the other hand,  normal conversations of Japanese people are in stead more of, I would say,  “resonance” of several tuning forks. They do their bests to show that they are listening to each other, by excessively nodding or just repeating “Really?”, but usually it seems hardly any constructive dialogues have been made.

*I sometimes feel you do not even need deep learning to simulate most of such Japanese conversations. Several-line Python codes would be enough.

My point is, this article series is mainly going to cover only a few techniques of NLP in deep learning field: sequence to sequence model (seq2seq model) , and especially Transformer. They are, at least for now, just mathematical models and mappings of a small part of this profound field of language (as far as I can cover in this article series). But still, examples of language would definitely help you understand Transformer model in the long run.

2 Tokens and word embedding

*Throughout my article series, “words” just means the normal words you use in daily life. “Tokens” means more general unit of NLP tasks. For example the word “Transformer” might be denoted as a single token “Transformer,” or maybe as a combination of two tokens “Trans” and “former.”

One challenging part of handling language data is its encodings. If you started learning programming in a language other than English, you would have encountered some troubles of using keyboards with different arrangements or with characters. Some comments on your codes in your native languages are sometimes not readable on some software. You can easily get away with that by using only English, but when it comes to NLP you have to deal with this difficulty seriously. How to encode characters in each language should be a first obstacle of NLP. In this article we are going to rely on a library named BPEmb, which provides word embedding in various languages, and you do not have to care so much about encodings in languages all over the world with this library.

In the first section, you might have noticed that Japanese sentence is not separated with spaces like Western languages. This is also true of Chinese language, and that means we need additional tasks of separating those sentences at least into proper chunks of words. This is not only a matter of engineering, but also of some linguistic fields. Also I think many people are not so conscious of how sentences in their native languages are grammatically separated.

The next point is, unlike other scientific data, such as temperature, velocity, voltage, or air pressure, language itself is not measured as numerical data. Thus in order to process language, including English, you first have to map language to certain numerical data, and after some processes you need to conversely map the output numerical data into language data. This section is going to be mainly about one-hot encoding and word embedding, the ways to convert word/token into numerical data. You might already have heard about this

You might have learnt about word embedding to some extent, but I hope you could get richer insight into this topic through this article.

2.1 One-hot encoding

One-hot encoding would be the most straightforward way to encode words/tokens. Assume that you have a dictionary whose size is |\mathcal{V}|, and it includes words from “a”, “ablation”, “actually” to “zombie”, “?”, “!”

In a mathematical manner, in order to choose a word out of those |\mathcal{V}| words, all you need is a |\mathcal{V}| dimensional vector, one of whose elements is 1, and the others are 0. When you want to choose the No. i word, which is “indeed” in the example below, its corresponding one-hot vector is \boldsymbol{v} = (0, \dots, 1, \dots, 0 ), where only the No. i element is 1. One-hot encoding is also easy to understand, and that’s all. It is easy to imagine that people have already come up with more complicated and better way to encoder words. And one major way to do that is word embedding.

2.2 Word embedding

Source: Francois Chollet, Deep Learning with Python,(2018), Manning

Actually word embedding is related to one-hot encoding, and if you understand how to train a simple neural network, for example densely connected layers, you would understand word embedding easily. The key idea of word embedding is denoting each token with a D dimensional vector, whose dimension is fewer than the vocabulary size |\mathcal{V}|. The elements of the resulting word embedding vector are real values, I mean not only 0 or 1. Obviously you can encode much richer variety of tokens with such vectors. The figure at the left side is from “Deep Learning with Python” by François Chollet, and I think this is an almost perfect and simple explanation of the comparison of one-hot encoding and word embedding. But the problem is how to get such convenient vectors. The answer is very simple: you have only to train a network whose inputs are one-hot vector of the vocabulary.

The figure below is a simplified model of word embedding of a certain word. When the word is input into a neural network, only the corresponding element of the one-hot vector is 1, and that virtually means the very first input layer is composed of one neuron whose value is 1. And the only one neuron propagates to the next D dimensional embedding layer. These weights are the very values which most other study materials call “an embedding vector.”

When you input each word into a certain network, for example RNN or Transformer, you map the input one-hot vector into the embedding layer/vector. The examples in the figure are how inputs are made when the input sentences are “You’ve got the touch” and “You’ve got the power.”   Assume that you have a dictionary of one-hot encoding, whose vocabulary is {“the”, “You’ve”, “Walberg”, “touch”, “power”, “Nights”, “got”, “Mark”, “Boogie”}, and the dimension of word embeding is 6. In this case |\mathcal{V}| = 9, D=6. When the inputs are “You’ve got the touch” or “You’ve got the power” , you put the one-hot vector corresponding to “You’ve”, “got”, “the”, “touch” or “You’ve”, “got”, “the”, “power” sequentially every time step t.

In order to get word embedding of certain vocabulary, you just need to train the network. We know that the words “actually” and “indeed” are used in similar ways in writings. Thus when we propagate those words into the embedding layer, we can expect that those embedding layers are similar. This is how we can mathematically get effective word embedding of certain vocabulary.

More interestingly, if word embedding is properly trained, you can mathematically “calculate” words. For example, \boldsymbol{v}_{king} - \boldsymbol{v}_{man} + \boldsymbol{v}_{woman} \approx \boldsymbol{v}_{queen}, \boldsymbol{v}_{Japan} - \boldsymbol{v}_{Tokyo} + \boldsymbol{v}_{Vietnam} \approx \boldsymbol{v}_{Hanoi}.

*I have tried to demonstrate this type of calculation on several word embedding, but none of them seem to work well. At least you should keep it in mind that word embedding learns complicated linear relations between words.

I should explain word embedding techniques such as word2vec in detail, but the main focus of this article is not NLP, so the points I have mentioned are enough to understand Transformer model with NLP examples in the upcoming articles.

 

3 Language model

Language models is one of the most straightforward, but crucial ideas in NLP. This is also a big topic, so this article is going to cover only basic points. Language model is a mathematical model of the probabilities of which words to come next, given a context. For example if you have a sentence “In the lecture, he opened a _.”, a language model predicts what comes at the part “_.” It is obvious that this is contextual. If you are talking about general university students, “_” would be “textbook,” but if you are talking about Japanese universities, especially in liberal art department, “_” would be more likely to be “smartphone. I think most of you use this language model everyday. When you type in something on your computer or smartphone, you would constantly see text predictions, or they might even correct your spelling or grammatical errors. This is language modelling. You can make language models in several ways, such as n-gram and neural language models, but in this article I can explain only general formulations for such models.

*I am not sure which algorithm is used in which services. That must be too fast changing and competitive for me to catch up.

As I mentioned in the first article series on RNN, a sentence is usually processed as sequence data in NLP. One single sentence is denoted as \boldsymbol{X} = (\boldsymbol{x}^{(1)}, \dots, \boldsymbol{x}^{(\tau)}), a list of vectors. The vectors are usually embedding vectors, and the (t) is the index of the order of tokens. For example the sentence “You’ve go the power.” can be expressed as \boldsymbol{X} = (\boldsymbol{x}^{(1)}, \boldsymbol{x}^{(2)}, \boldsymbol{x}^{(3)}, \boldsymbol{x}^{(4)}), where \boldsymbol{x}^{(1)}, \boldsymbol{x}^{(2)}, \boldsymbol{x}^{(3)}, \boldsymbol{x}^{(4)} denote “You’ve”, “got”, “the”, “power”, “.” respectively. In this case \tau = 4.

In practice a sentence \boldsymbol{X} usually includes two tokens BOS and EOS at the beginning and the end of the sentence. They mean “Beginning Of Sentence” and “End Of Sentence” respectively. Thus in many cases \boldsymbol{X} = (\boldsymbol{BOS} , \boldsymbol{x}^{(1)}, \dots, \boldsymbol{x}^{(\tau)}, \boldsymbol{EOS} ). \boldsymbol{BOS} and \boldsymbol{EOS} are also both vectors, at least in the Tensorflow tutorial.

P(\boldsymbol{X} = (\boldsymbol{BOS}, \boldsymbol{x}^{(1)}, \dots, \boldsymbol{x}^{(\tau)}, \boldsymbol{EOS}) is the probability of incidence of the sentence. But it is easy to imagine that it would be very hard to directly calculate how likely the sentence \boldsymbol{X} appears out of all possible sentences. I would rather say it is impossible. Thus instead in NLP we calculate the probability P(\boldsymbol{X}) as a product of the probability of incidence or a certain word, given all the words so far. When you’ve got the words (\boldsymbol{x}^{(1)}, \dots, \boldsymbol{x}^{(t-1}) so far, the probability of the incidence of \boldsymbol{x}^{(t)}, given the context is  P(\boldsymbol{x}^{(t)}|\boldsymbol{x}^{(1)}, \dots, \boldsymbol{x}^{(t-1)}). P(\boldsymbol{BOS}) is a probability of the the sentence \boldsymbol{X} being (\boldsymbol{BOS}), and the probability of \boldsymbol{X} being (\boldsymbol{BOS}, \boldsymbol{x}^{(1)}) can be decomposed this way: P(\boldsymbol{BOS}, \boldsymbol{x}^{(1)}) = P(\boldsymbol{x}^{(1)}|\boldsymbol{BOS})P(\boldsymbol{BOS}).

Just as well P(\boldsymbol{BOS}, \boldsymbol{x}^{(1)}, \boldsymbol{x}^{(2)}) = P(\boldsymbol{x}^{(2)}| \boldsymbol{BOS}, \boldsymbol{x}^{(1)}) P( \boldsymbol{BOS}, \boldsymbol{x}^{(1)})= P(\boldsymbol{x}^{(2)}| \boldsymbol{BOS}, \boldsymbol{x}^{(1)}) P(\boldsymbol{x}^{(1)}| \boldsymbol{BOS}) P( \boldsymbol{BOS}).

Hence, the general probability of incidence of a sentence \boldsymbol{X} is P(\boldsymbol{X})=P(\boldsymbol{BOS}, \boldsymbol{x}^{(1)}, \boldsymbol{x}^{(2)}, \dots, \boldsymbol{x}^{(\tau -1)}, \boldsymbol{x}^{(\tau)}, \boldsymbol{EOS}) = P(\boldsymbol{EOS}| \boldsymbol{BOS}, \boldsymbol{x}^{(1)}, \dots, \boldsymbol{x}^{(\tau)}) P(\boldsymbol{x}^{(\tau)}| \boldsymbol{BOS}, \boldsymbol{x}^{(1)}, \dots, \boldsymbol{x}^{(\tau - 1)}) \cdots P(\boldsymbol{x}^{(2)}| \boldsymbol{BOS}, \boldsymbol{x}^{(1)}) P(\boldsymbol{x}^{(1)}| \boldsymbol{BOS}) P(\boldsymbol{BOS}).

Let \boldsymbol{x}^{(0)} be \boldsymbol{BOS} and \boldsymbol{x}^{(\tau + 1)} be \boldsymbol{EOS}. Plus, let P(\boldsymbol{x}^{(t+1)}|\boldsymbol{X}_{[0, t]}) be P(\boldsymbol{x}^{(t+1)}|\boldsymbol{x}^{(0)}, \dots, \boldsymbol{x}^{(t)}), then P(\boldsymbol{X}) = P(\boldsymbol{x}^{(0)})\prod_{t=0}^{\tau}{P(\boldsymbol{x}^{(t+1)}|\boldsymbol{X}_{[0, t]})}. Language models calculate which words to come sequentially in this way.

Here’s a question: how would you evaluate a language model?

I would say the answer is, when the language model generates words, the more confident the language model is, the better the language model is. Given a context, when the distribution of the next word is concentrated on a certain word, we can say the language model is confident about which word to come next, given the context.

*For some people, it would be more understandable to call this “entropy.”

Let’s take the vocabulary {“the”, “You’ve”, “Walberg”, “touch”, “power”, “Nights”, “got”, “Mark”, “Boogie”} as an example. Assume that P(\boldsymbol{X}) = P(\boldsymbol{BOS}, \boldsymbol{You've}, \boldsymbol{got}, \boldsymbol{the}, \boldsymbol{touch}, \boldsymbol{EOS}) = P(\boldsymbol{BOS}, \boldsymbol{x}^{(1)}, \boldsymbol{x}^{(2)}, \boldsymbol{x}^{(3)}, \boldsymbol{x}^{(4)}, \boldsymbol{EOS})= P(\boldsymbol{x}^{(0)})\prod_{t=0}^{4}{P(\boldsymbol{x}^{(t+1)}|\boldsymbol{X}_{[0, t]})}. Given a context (\boldsymbol{BOS}, \boldsymbol{x}^{(1)}), the probability of incidence of \boldsymbol{x}^{(2)} is P(\boldsymbol{x}^{2}|\boldsymbol{BOS}, \boldsymbol{x}^{(1)}). In the figure below, the distribution at the left side is less confident because probabilities do not spread widely, on the other hand the one at the right side is more confident that next word is “got” because the distribution concentrates on “got”.

*You have to keep it in mind that the sum of all possible probability P(\boldsymbol{x}^{(2)} | \boldsymbol{BOS}, \boldsymbol{x}^{(1)}) is 1, that is, P(\boldsymbol{the}| \boldsymbol{BOS}, \boldsymbol{x}^{(1)}) + P(\boldsymbol{You've}| \boldsymbol{BOS}, \boldsymbol{x}^{(1)}) + \cdots + P(\boldsymbol{Boogie}| \boldsymbol{BOS}, \boldsymbol{x}^{(1)}) = 1.

While the language model generating the sentence “BOS You’ve got the touch EOS”, it is better if the language model keeps being confident. If it is confident, P(\boldsymbol{X})= P(\boldsymbol{BOS}) P(\boldsymbol{x}^{(1)}|\boldsymbol{BOS}}P(\boldsymbol{x}^{(3)}|\boldsymbol{BOS}, \boldsymbol{x}^{(1)}, \boldsymbol{x}^{(2)}) P(\boldsymbol{x}^{(4)}|\boldsymbol{BOS}, \boldsymbol{x}^{(1)}, \boldsymbol{x}^{(2)}, \boldsymbol{x}^{(3)}) P(\boldsymbol{EOS}|\boldsymbol{BOS}, \boldsymbol{x}^{(1)}, \boldsymbol{x}^{(2)}, \boldsymbol{x}^{(3)}, \boldsymbol{x}^{(4)})} gets higher. Thus (-1) \{ log_{b}{P(\boldsymbol{BOS})} + log_{b}{P(\boldsymbol{x}^{(1)}|\boldsymbol{BOS}}) + log_{b}{P(\boldsymbol{x}^{(3)}|\boldsymbol{BOS}, \boldsymbol{x}^{(1)}, \boldsymbol{x}^{(2)})} + log_{b}{P(\boldsymbol{x}^{(4)}|\boldsymbol{BOS}, \boldsymbol{x}^{(1)}, \boldsymbol{x}^{(2)}, \boldsymbol{x}^{(3)})} + log_{b}{P(\boldsymbol{EOS}|\boldsymbol{BOS}, \boldsymbol{x}^{(1)}, \boldsymbol{x}^{(2)}, \boldsymbol{x}^{(3)}, \boldsymbol{x}^{(4)})} \} gets lower, where usually b=2 or b=e.

This is how to measure how confident language models are, and the indicator of the confidence is called perplexity. Assume that you have a data set for evaluation \mathcal{D} = (\boldsymbol{X}_1, \dots, \boldsymbol{X}_n, \dots, \boldsymbol{X}_{|\mathcal{D}|}), which is composed of |\mathcal{D}| sentences in total. Each sentence \boldsymbol{X}_n = (\boldsymbol{x}^{(0)})\prod_{t=0}^{\tau ^{(n)}}{P(\boldsymbol{x}_{n}^{(t+1)}|\boldsymbol{X}_{n, [0, t]})} has \tau^{(n)} tokens in total excluding \boldsymbol{BOS}, \boldsymbol{EOS}. And let |\mathcal{V}| be the size of the vocabulary of the language model. Then the perplexity of the language model is b^z, where z = \frac{-1}{|\mathcal{V}|}\sum_{n=1}^{|\mathcal{D}|}{\sum_{t=0}^{\tau ^{(n)}}{log_{b}P(\boldsymbol{x}_{n}^{(t+1)}|\boldsymbol{X}_{n, [0, t]})}. The b is usually 2 or e.

For example, assume that \mathcal{V} is vocabulary {“the”, “You’ve”, “Walberg”, “touch”, “power”, “Nights”, “got”, “Mark”, “Boogie”}. Also assume that the evaluation data set for perplexity of a language model is \mathcal{D} = (\boldsymbol{X}_1, \boldsymbol{X}_2), where \boldsymbol{X_1} =(\boldsymbol{You've}, \boldsymbol{got}, \boldsymbol{the}, \boldsymbol{touch}) \boldsymbol{X_2} = (\boldsymbol{You've}, \boldsymbol{got}, \boldsymbol{the }, \boldsymbol{power}). In this case |\mathcal{V}|=9, |\mathcal{D}|=2. I have already showed you how to calculate the perplexity of the sentence “You’ve got the touch.” above. You just need to do a similar thing on another sentence “You’ve got the power”, and then you can get the perplexity of the language model.

*If the network is not properly trained, it would also be confident of generating wrong outputs. However, such network still would give high perplexity because it is “confident” at any rate. I’m sorry I don’t know how to tackle the problem. Please let me put this aside, and let’s get down on Transformer model soon.

Appendix

Let’s see how word embedding is implemented with a very simple example in the official Tensorflow tutorial. It is a simple binary classification task on IMDb Dataset. The dataset is composed to comments on movies by movie critics, and you have only to classify if the commentary is positive or negative about the movie. For example when you get you get an input “To be honest, Michael Bay is a terrible as an action film maker. You cannot understand what is going on during combat scenes, and his movies rely too much on advertisements. I got a headache when Mark Walberg used a Chinese cridit card in Texas. However he is very competent when it comes to humorous scenes. He is very talented as a comedy director, and I have to admit I laughed a lot.“, the neural netowork has to judge whether the statement is positive or negative.

This networks just takes an average of input embedding vectors and regress it into a one dimensional value from 0 to 1. The shape of embedding layer is (8185, 16). Weights of neural netowrks are usually implemented as matrices, and you can see that each row of the matrix corresponds to emmbedding vector of each token.

*It is easy to imagine that this technique is problematic. This network virtually taking a mean of input embedding vectors. That could mean if the input sentence includes relatively many tokens with negative meanings, it is inclined to be classified as negative. But for example, if the sentence is “This masterpiece is a dark comedy by Charlie Chaplin which depicted stupidity of the evil tyrant gaining power in the time. It thoroughly mocked Germany in the time as an absurd group of fanatics, but such propaganda could have never been made until ‘Casablanca.'” , this can be classified as negative, because only the part “masterpiece” is positive as a token, and there are much more words with negative meanings themselves.

The official Tensorflow tutorial provides visualization of word embedding with Embedding Projector, but I would like you to take more control over the data by yourself. Please just copy and paste the codes below, installing necessary libraries. You would get a map of vocabulary used in the text classification task. It seems you cannot find clear tendency of the clusters of the tokens. You can try other dimension reduction methods to get maps of the vocabulary by for example using Scikit Learn.

import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
import tensorflow_datasets as tfds
tfds.disable_progress_bar()

(train_data, test_data), info = tfds.load(
    'imdb_reviews/subwords8k', 
    split = (tfds.Split.TRAIN, tfds.Split.TEST), 
    with_info=True, as_supervised=True)

train_batches = train_data.shuffle(1000).padded_batch(10)
test_batches = test_data.shuffle(1000).padded_batch(10)

embedding_dim=16

encoder = info.features['text'].encoder

model = keras.Sequential([
  layers.Embedding(encoder.vocab_size, embedding_dim),
  layers.GlobalAveragePooling1D(),
  layers.Dense(16, activation='relu'),
  layers.Dense(1)
])

print("\n\nThe size of the vocabulary generated from IMDb Dataset is " + str(encoder.vocab_size) + '\n\n')

model.summary()

model.compile(optimizer='adam',
              loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
              metrics=['accuracy'])

history = model.fit(
    train_batches,
    epochs=10,
    validation_data=test_batches, validation_steps=20)

word_embedding_vectors = model.layers[0].get_weights()[0]

print("\n\nThe shape of the trained weigths of the embedding layer is " + str(word_embedding_vectors.shape) + '\n\n')

from sklearn.manifold import TSNE
X_reduced = TSNE(n_components = 2, init='pca', random_state=0).fit_transform(word_embedding_vectors)

import numpy as np
embedding_dict = zip(encoder.subwords, np.arange(len(encoder.subwords)))
embedding_dict = dict(embedding_dict)

import matplotlib.pyplot as plt

plt.figure(figsize=(60, 45))
plt.scatter(X_reduced[:, 0], X_reduced[:, 1])

for i in range(0, len(encoder.subwords), 5):
    plt.text(X_reduced[i, 0], X_reduced[i, 1], encoder.subwords[i], fontsize=20, color='red')
plt.title("The map of vocabulary of IMDb Dataset mapped to a 2 dimensional space by t-SNE", fontsize=60)
#plt.savefig('imdb_tsne_map.png')
plt.show()

 

 

 

 

 

Yasuto Tamura

Instructions on Transformer for people outside NLP field, but with examples of NLP

/in , , , , , , , , /by

I found it quite difficult to explain mathematical details of long short-term memory (LSTM) in my previous article series. But when I was studying LSTM, a new promising algorithm was already attracting attentions. The algorithm is named Transformer. Its algorithm was a first announced in a paper named “Attention Is All You Need,” and it outperformed conventional translation algorithms with lower computational costs.

In this article series, I am going to provide explanations on minimum prerequisites for understanding deep learning in NLP (natural language process) tasks, but NLP is not the main focus of this article series, and actually I do not study in NLP field. I think Transformer is going to be a new major model of deep learning as well as CNN or RNN, and the model is now being applied in various fields.

Even though Transformer is going to be a very general deep learning model, I still believe it would be an effective way to understand Transformer with some NLP because language is a good topic we have in common. Unlike my previous article series, in which I tried to explain theoretical side of RNN as precisely as possible, in this article I am going to focus on practical stuff with my toy implementations of NLP tasks, largely based on Tensorflow official tutorial. But still I will do my best to make it as straightforward as possible to understand the architecture of Transformer with various original figures.

This series is going to be composed of the articles below.

If you are in the field and can read the codes in the official tutorial with no questions, this article series is not for you, but if you want to see how a Transformer works but do not want to go too much into details of NLP, this article would be for you.

Simple RNN
Yasuto Tamura

LSTM back propagation: following the flows of variables

/in , , , /by

First of all, the summary of this article is: please just download my Power Point slides which I made and be patient, following the equations.

I am not supposed to use so many mathematics when I write articles on Data Science Blog. However using little mathematics when I talk about LSTM backprop is like writing German, never caring about “der,” “die,” “das,” or speaking little English in English classes (which most high school English teachers in Japan do) or writing Japanese without using any Chinese characters (which looks like a terrible handwriting by a drug addict). In short, that is ridiculous. And all the precise equations of LSTM backprop, written on a Blog is not a comfortable thing to see. So basically the whole of this article is an advertisement on my PowerPoint slides, sponsored by DATANOMIQ, and I can just give you some tips to get ready for the most tiresome part of understanding LSTM here.

*This article is the fifth article of “A gentle introduction to the tiresome part of understanding RNN.”

 *In this article “Densely Connected Layers” is written as “DCL,” and “Convolutional Neural Network” as “CNN.”

1. Chain rules

This article is virtually an article on chain rules of differentiation. Even if you have clear understandings on chain rules, I recommend you to take a look at this section. If you have written down all the equations of back propagation of DCL, you would have seen what chain rules are. Even simple chain rules for backprop of normal DCL can be difficult to some people, but when it comes to backprop of LSTM, it is a pure torture.  I think using graphical models would help you understand what chain rules are like. Graphical models are basically used to describe the relations of variables and functions in probabilistic models, so to be exact I am going to use “something like graphical models” in this article. Not that this is a common way to explain chain rules.

First, let’s think about the simplest type of chain rule. Assume that you have a function f=f(x)=f(x(y)), and relations of the functions are displayed as the graphical model at the left side of the figure below. Variables are a type of function, so you should think that every node in graphical models denotes a function. Arrows in purple in the right side of the chart show how information propagate in differentiation.

Next, if you a function f , which has two variances  x_1 and x_2. And both of the variances also share two variances  y_1 and y_2. When you take partial differentiation of f with respect to y_1 or y_2, the formula is a little tricky. Let’s think about how to calculate \frac{\partial f}{\partial y_1}. The variance y_1 propagates to f via x_1 and x_2. In this case the partial differentiation has two terms as below.

In chain rules, you have to think about all the routes where a variance can propagate through. If you generalize chain rules, that is like below, and you need to understand chain rules in this way to understanding any types of back propagation.

The figure above shows that if you calculate partial differentiation of f with respect to y_i, the partial differentiation has n terms in total because y_i propagates to f via n variances. In order to understand backprop of LSTM, you constantly have to care about the flow of variances, which I showed as arrows in purple above.

2. Chain rules in LSTM

I would like you to remember the figure below, which I used in the second article to show how errors propagate backward during backprop of simple RNNs. After forward propagation, first of all, you need to calculate \frac{\partial J}{\partial \boldsymbol{\theta}^{(t)}}, gradients of the error function with respect to parameters, at every time step. But you have to be careful that even though these gradients depend on time steps, the parameters \boldsymbol{\theta} do not depend on time steps.

*As I mentioned in the second article I personally think \frac{\partial J}{\partial \boldsymbol{\theta}^{(t)}} should be rather denoted as (\frac{\partial J}{\partial \boldsymbol{\theta}})^{(t)} because parameters themselves do not depend on time. The textbook by MIT press also partly use the former notation. And you are likely to encounter this type of notation, so I think it is not bad to get ready for both.

The errors at time step (t) propagate backward to all the \boldsymbol{h} ^{(s)}, (s \leq t). Conversely, in order to calculate \frac{\partial J}{\partial \boldsymbol{\theta}^{(t)}} errors flowing from J^{(s)}, (s \geq t). In the chart you need arrows of errors in purple for the gradient in a purple frame, orange arrows for gradients in orange frame, red arrows for gradients in red frame. And you need to sum up \frac{\partial J}{\partial \boldsymbol{\theta}^{(t)}} to calculate \frac{\partial J}{\partial \boldsymbol{\theta}} = \sum_{t}{\frac{\partial J}{\partial \boldsymbol{\theta}^{(t)}}}, and you need this gradient \frac{\partial J}{\partial \boldsymbol{\theta}} to renew parameters, one time.

At an RNN block level, the flows of errors and how to renew parameters are the same in LSTM backprop, but the flow of errors inside each block is much more complicated in LSTM backprop. And in this article and my PowerPoint slides, I use a special notation to denote errors: \delta \star ^{(t)}= \frac{\partial J^{(t)}}{\partial \star}

* Again, please be careful of what \delta \star ^{(t)} means. Neurons depend on time steps, but parameters do not depend on time steps. So if \star are neurons,  \delta \star ^{(t)}= \frac{\partial J}{ \partial \star ^{(t)}}, but when \star are parameters, \delta \star ^{(t)}= \frac{\partial J^{(t)}}{ \partial \star} should be rather denoted like \delta \star ^{(t)}= (\frac{\partial J}{ \partial \star ^{(t)}}). In the Space Odyssey paper,  \boldsymbol{\star} are not used as parameters, but in my PowerPoint slides and some other materials, \boldsymbol{\star} are used also as parameteres.

As I wrote in the last article, you calculate \boldsymbol{f}^{(t)}, \boldsymbol{i}^{(t)}, \boldsymbol{z}^{(t)}, \boldsymbol{o}^{(t)} as below. Unlike the last article, I also added the terms of peephole connections in the equations below, and I also added the variances \bar{\boldsymbol{f}^{(t)}}, \bar{\boldsymbol{i}^{(t)}}, \bar{\boldsymbol{z}^{(t)}}, \bar{\boldsymbol{o}^{(t)}} for convenience.

  • \boldsymbol{\bar{f}}^{(t)}=\boldsymbol{W}_{for} \cdot \boldsymbol{x}^{(t)} + \boldsymbol{R}_{for} \cdot \boldsymbol{y}^{(t-1)} + \boldsymbol{p}_{for}\odot \boldsymbol{c}^{(t-1)} + \boldsymbol{b}_{for}
  • \boldsymbol{\bar{i}}^{(t)}=\boldsymbol{W}_{in} \cdot \boldsymbol{x}^{(t)} + \boldsymbol{R}_{in} \cdot \boldsymbol{y}^{(t-1)} + \boldsymbol{p}_{in}\odot \boldsymbol{c}^{(t-1)} + \boldsymbol{b}_{in}
  • \boldsymbol{\bar{z}}^{(t)}=\boldsymbol{W}_z \cdot \boldsymbol{x}^{(t)} + \boldsymbol{R}_z \cdot \boldsymbol{y}^{(t-1)} + \boldsymbol{b}_z
  • \boldsymbol{\bar{o}}^{(t)}=\boldsymbol{W}_{out} \cdot \boldsymbol{x}^{(t)} + \boldsymbol{R}_{out} \cdot \boldsymbol{y}^{(t-1)} + \boldsymbol{p}_{out}\odot \boldsymbol{c}^{(t)} + \boldsymbol{b}_{out}
  • \boldsymbol{f}^{(t)}=\sigma( \boldsymbol{\bar{f}}^{(t)})
  • \boldsymbol{i}^{(t)}=\sigma(\boldsymbol{\bar{i}}^{(t)})
  • \boldsymbol{z}^{(t)}=tanh(\boldsymbol{\bar{z}}^{(t)})
  • \boldsymbol{o}^{(t)}=\sigma(\boldsymbol{\bar{o}}^{(t)})

With  Hadamar product operator, the renewed cell and the output are calculated as below.

  • \boldsymbol{c}^{(t)} = \boldsymbol{z}^{(t)}\odot \boldsymbol{i}^{(t)} + \boldsymbol{c}^{(t-1)} \odot \boldsymbol{f}^{(t)}
  • \boldsymbol{y}^{(t)} = \boldsymbol{o}^{(t)} \odot tanh(\boldsymbol{c}^{(t)})

In this article I would rather give instructions on how to read my PowerPoint slide. Just as general backprop, you need to calculate gradients of error functions with respect to parameters, such as \delta \boldsymbol{W}_{\star}, \delta \boldsymbol{R}_{\star}, \delta \boldsymbol{p}_{\star}, \delta \boldsymbol{b}_{\star}, where \star is either of \{z, in, for, out \}. And just as backprop of simple RNNs, in order to calculate gradients with respect to parameters, you need to calculate errors of neurons, that is gradients of error functions with respect to neurons, such as \delta \boldsymbol{f}^{(t)}, \delta \boldsymbol{i}^{(t)}, \delta \boldsymbol{z}^{(t)}, \delta \boldsymbol{o}^{(t)}.

*Again and again, keep it in mind that neurons depend on time steps, but parameters do not depend on time steps.

When you calculate gradients with respect to neurons, you can first calculate \delta \boldsymbol{y}^{(t)}, but the equation for this error is the most difficult, so I recommend you to put it aside for now. After calculating \delta \boldsymbol{y}^{(t)}, you can next calculate \delta \bar{\boldsymbol{o}}^{(t)}= \frac{\partial J^{(t)}}{ \partial \bar{\boldsymbol{o}}^{(t)}}. If you see the LSTM block below as a graphical model which I introduced, the information of \bar{\boldsymbol{o}}^{(t)} flow like the purple arrows. That means, \bar{\boldsymbol{o}}^{(t)} affects J only via \boldsymbol{y}^{(t)}, and this structure is equal to the first graphical model which I have introduced above. And if you calculate \bar{\boldsymbol{o}}^{(t)} element-wise, you get the equation \delta \bar{o}_{k}^{(t)}=\frac{\partial J}{\partial \bar{o}_{k}^{(t)}}= \frac{\partial J}{\partial y_{k}^{(t)}} \frac{\partial y_{k}^{(t)}}{\partial \bar{o}_{k}^{(t)}}.

*The k is an index of an element of vectors. If you can calculate element-wise gradients, it is easy to understand that as differentiation of vectors and matrices.

Next you can calculate \delta \boldsymbol{c}^{(t)}, and chain rules are very important in this process. The flow of \delta \boldsymbol{c}^{(t)} to J can be roughly divided into two streams: the one flows to J as \bodlsymbol{y}^{(t)}, and the one flows to J as \bodlsymbol{c}^{(t+1)}. And the stream from \bodlsymbol{c}^{(t)} to \bodlsymbol{y}^{(t)} also have two branches: the one via \bar{\boldsymbol{o}}^{(t)} and the one which directly converges as  \bodlsymbol{y}^{(t)}. Just as well, the stream from \bodlsymbol{c}^{(t)} to \bodlsymbol{c}^{(t+1)} also have three branches: the ones via \bar{\boldsymbol{f}}^{(t)}, \bar{\boldsymbol{i}}^{(t)}, and the one which directly converges as \bodlsymbol{c}^{(t+1)}.

If you see see these flows as graphical a graphical model, that would be like the figure below.

According to this graphical model, you can calculate \delta \boldsymbol{c} ^{(t)} element-wise as below.

* TO BE VERY HONEST I still do not fully understand why we can apply chain rules like above to calculate \delta \boldsymbol{c}^{(t)}. When you apply the formula of chain rules, which I showed in the first section, to this case, you have to be careful of where to apply partial differential operators \frac{\partial}{ \partial c_{k}^{(t)}}. In the case above, in the part \frac{\partial y_{k}^{(t)}}{\partial c_{k}^{(t)}} the partial differential operator only affects tanh(c_{k}^{(t)}) of o_{k}^{(t)} \cdot tanh(c_{k}^{(t)}), and in the part \frac{\partial c_{k}^{(t+1)}}{\partial c_{k}^{(t)}}, the partial differential operator \frac{\partial}{\partial c_{k}^{(t)}} only affects the part c_{k}^{(t)} of the term c^{t}_{k} \cdot f_{k}^{(t+1)}. In the \frac{\partial \bar{o}_{k}^{(t)}}{\partial c_{k}^{(t)}} part, only (p_{out})_{k} \cdot c_{k}^{(t)},  in the \frac{\partial \bar{i}_{k}^{(t+1)}}{\partial c_{k}^{(t)}} part, only (p_{in})_{k} \cdot c_{k}^{(t)}, and in the \frac{\partial \bar{f}_{k}^{(t+1)}}{\partial c_{k}^{(t)}} part, only (p_{in})_{k} \cdot c_{k}^{(t)}. But some other parts, which are not affected by \frac{\partial}{ \partial c_{k}^{(t)}} are also functions of c_{k}^{(t)}. For example o_{k}^{(t)} of o_{k}^{(t)} \cdot tanh(c_{k}^{(t)}) is also a function of c_{k}^{(t)}. And I am still not sure about the logic behind where to affect those partial differential operators.

*But at least, these are the only decent equations for LSTM backprop which I could find, and a frequently cited paper on LSTM uses implementation based on these equations. Computer science is more of practical skills, rather than rigid mathematical logic. It  If you have any comments or advice on this point, please let me know.

Calculating \delta \bar{\boldsymbol{f}}^{(t)}, \delta \bar{\boldsymbol{i}}^{(t)}, \delta \bar{\boldsymbol{z}}^{(t)} are also relatively straigtforward as calculating \delta \bar{\boldsymbol{o}}^{(t)}. They all use the first type of chain rule in the first section. Thereby you can get these gradients: \delta \bar{f}_{k}^{(t)}=\frac{\partial J}{ \partial \bar{f}_{k}^{(t)}} =\frac{\partial J}{\partial c_{k}^{(t)}} \frac{\partial c_{k}^{(t)}}{ \partial \bar{f}_{k}^{(t)}}, \delta \bar{i}_{k}^{(t)}=\frac{\partial J}{\partial \bar{i}_{k}^{(t)}} =\frac{\partial J}{\partial c_{k}^{(t)}} \frac{\partial c_{k}^{(t)}}{ \partial \bar{i}_{k}^{(t)}}, and \delta \bar{z}_{k}^{(t)}=\frac{\partial J}{\partial \bar{z}_{k}^{(t)}} =\frac{\partial J}{\partial c_{k}^{(t)}} \frac{\partial c_{k}^{(t)}}{ \partial \bar{i}_{k}^{(t)}}.

All the gradients which we have calculated use the error \delta \boldsymbol{y}^{(t)}, but when it comes to calculating \delta \boldsymbol{y}^{(t)}….. I can only say “Please be patient. I did my best in my PowerPoint slides to explain that.” It is not a kind of process which I want to explain on Word Press. In conclusion you get an error like this: \delta \boldsymbol{y}^{(t)}=\frac{\partial J^{(t)}}{\partial \boldsymbol{y}^{(t)}} + \boldsymbol{R}_{for}^{T} \delta \bar{\boldsymbol{f}}^{(t+1)} + \boldsymbol{R}_{in}^{T}\delta \bar{\boldsymbol{i}}^{(t+1)} + \boldsymbol{R}_{out}^{T}\delta \bar{\boldsymbol{o}}^{(t+1)} + \boldsymbol{R}_{z}^{T}\delta \bar{\boldsymbol{z}}^{(t+1)}, and the flows of \boldsymbol{y}^{(t)} are as blow.

Combining the gradients we have got so far, we can calculate gradients with respect to parameters. For concrete results, please check the Space Odyssey paper or my PowerPoint slide.

3. How LSTMs tackle exploding/vanishing gradients problems

*If you are allergic to mathematics, you should not read this section or download my PowerPoint slide.

*Part of this section is more or less subjective, so if you really want to know how LSTM mitigate the problems, I highly recommend you to also refer to other materials. But at least I did my best for this article.

LSTMs do not completely solve, vanishing gradient problems. They mitigate vanishing/exploding gradient problems. I am going to roughly explain why they can tackle those problems. I think you find many explanations on that topic, but many of them seems to have some mathematical mistakes (even the slide used in a lecture in Stanford University) and I could not partly agree with some statements. I also could not find any papers or materials which show the whole picture of how LSTMs can tackle those problems. So in this article I am only going to give instructions on the most mainstream way to explain this topic.

First let’s see how gradients actually “vanish” or “explode” in simple RNNs. As I in the second article of this series, simple RNNs propagate forward as the equations below.

  • \boldsymbol{a}^{(t)} = \boldsymbol{b} + \boldsymbol{W} \cdot \boldsymbol{h}^{(t-1)} + \boldsymbol{U} \cdot \boldsymbol{x}^{(t)}
  • \boldsymbol{h}^{(t)}= g(\boldsymbol{a}^{(t)})
  • \boldsymbol{o}^{(t)} = \boldsymbol{c} + \boldsymbol{V} \cdot \boldsymbol{h}^{(t)}
  • \hat{\boldsymbol{y}} ^{(t)} = f(\boldsymbol{o}^{(t)})

And every time step, you get an error function J^{(t)}. Let’s consider the gradient of J^{(t)} with respect to \boldsymbol{h}^{(k)}, that is the error flowing from J^{(t)} to \boldsymbol{h}^{(k)}. This error is the most used to calculate gradients of the parameters.

If you calculate this error more concretely, \frac{\partial J^{(t)}}{\partial \boldsymbol{h}^{(k)}} = \frac{\partial J^{(t)}}{\partial \boldsymbol{h}^{(t)}} \frac{\partial \boldsymbol{h}^{(t)}}{\partial \boldsymbol{h}^{(t-1)}} \cdots \frac{\partial \boldsymbol{h}^{(k+2)}}{\partial \boldsymbol{h}^{(k+1)}} \frac{\partial \boldsymbol{h}^{(k+1)}}{\partial \boldsymbol{h}^{(k)}} = \frac{\partial J^{(t)}}{\partial \boldsymbol{h}^{(t)}} \prod_{k< s \leq t} \frac{\partial \boldsymbol{h}^{(s)}}{\partial \boldsymbol{h}^{(s-1)}}, where \frac{\partial \boldsymbol{h}^{(s)}}{\partial \boldsymbol{h}^{(s-1)}} = \boldsymbol{W} ^T \cdot diag(g'(\boldsymbol{b} + \boldsymbol{W}\cdot \boldsymbol{h}^{(s-1)} + \boldsymbol{U}\cdot \boldsymbol{x}^{(s)})) = \boldsymbol{W} ^T \cdot diag(g'(\boldsymbol{a}^{(s)})).

* If you see the figure as a type of graphical model, you should be able to understand the why chain rules can be applied as the equation above.

*According to this paper \frac{\partial \boldsymbol{h}^{(s)}}{\partial \boldsymbol{h}^{(s-1)}} = \boldsymbol{W} ^T \cdot diag(g'(\boldsymbol{a}^{(s)})), but it seems that many study materials and web sites are mistaken in this point.

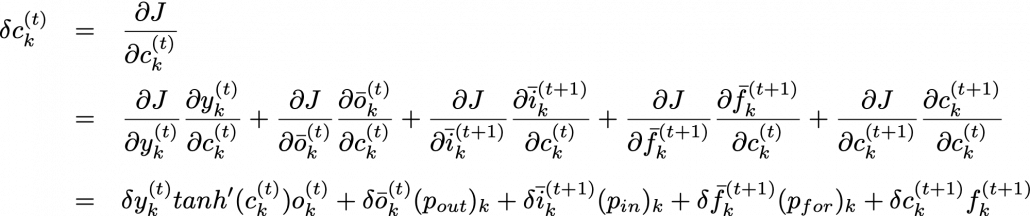
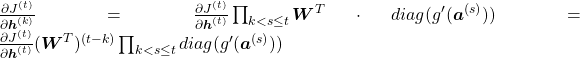Hence \frac{\partial J^{(t)}}{\partial \boldsymbol{h}^{(k)}} = \frac{\partial J^{(t)}}{\partial \boldsymbol{h}^{(t)}} \prod_{k< s \leq t} \boldsymbol{W} ^T \cdot diag(g'(\boldsymbol{a}^{(s)})) = \frac{\partial J^{(t)}}{\partial \boldsymbol{h}^{(t)}} (\boldsymbol{W} ^T )^{(t - k)} \prod_{k< s \leq t} diag(g'(\boldsymbol{a}^{(s)})). If you take norms of the members you get an equality \left\lVert \frac{\partial J^{(t)}}{\partial \boldsymbol{h}^{(k)}} \right\rVert \leq \left\lVert \frac{\partial J^{(t)}}{\partial \boldsymbol{h}^{(t)}} \right\rVert \left\lVert \boldsymbol{W} ^T \right\rVert ^{(t - k)} \prod_{k< s \leq t} \left\lVert diag(g'(\boldsymbol{a}^{(s)}))\right\rVert. I will not go into detail anymore, but it is known that according to this inequality, multiplication of weight vectors exponentially converge to 0 or to infinite number.

We have seen that the error \frac{\partial J^{(t)}}{\partial \boldsymbol{h}^{(k)}} is the main factor causing vanishing/exploding gradient problems. In case of LSTM, \frac{\partial J^{(t)}}{\partial \boldsymbol{c}^{(k)}} is an equivalent. For simplicity, let’s calculate only \frac{\partial \boldsymbol{c}^{(t)}}{\partial \boldsymbol{c}^{(t-1)}}, which is equivalent to \frac{\partial \boldsymbol{h}^{(t)}}{\partial \boldsymbol{h}^{(t-1)}} of simple RNN backprop.

* Just as I noted above, you have to be careful of which part the partial differential operator \frac{\partial}{\partial \boldsymbol{c}^{(t-1)}} affects in the chain rule above. That is, you need to calculate \frac{\partial}{\partial \boldsymbol{c}^{(t-1)}} (\boldsymbol{c}^{(t-1)} \odot \boldsymbol{f}^{(t)}), and the partial differential operator only affects \boldsymbol{c}^{(t-1)}. I think this is not a correct mathematical notation, but please forgive me for doing this for convenience.

If you continue calculating the equation above more concretely, you get the equation below.

I cannot mathematically explain why, but it is known that this characteristic of gradients of LSTM backprop mitigate the vanishing/exploding gradient problem. We have seen that if you take a norm of \frac{\partial J^{(t)}}{\partial \boldsymbol{h}^{(k)}}, that is equal or smaller than repeated multiplication of the norm of the same weight matrix, and that soon leads to vanishing/exploding gradient problem. But according to the equation above, even if you take a norm of repeatedly multiplied \frac{\partial \boldsymbol{c}^{(t)}}{\partial \boldsymbol{c}^{(t-1)}}, its norm cannot be evaluated with a simple value like repeated multiplication of the norm of the same weight matrix. The outputs of each gate are different from time steps to time steps, and that adjust the value of \frac{\partial \boldsymbol{c}^{(t)}}{\partial \boldsymbol{c}^{(t-1)}}.

*I personally guess the item diag(\boldsymbol{f}^{(t)}) is every effective. The unaffected value of can directly diag(\boldsymbol{f}^{(t)}) adjust the value of \frac{\partial \boldsymbol{c}^{(t)}}{\partial \boldsymbol{c}^{(t-1)}}. And as a matter of fact, it is known that performances of LSTM drop the most when you gite rid of forget gates.

When it comes to tackling exploding gradient problems, there is a much easier technique called gradient clipping. This algorithm is very simple: you just have to adjust the size of gradient so that the absolute value of gradient is under a threshold at every time step. Imagine that you decide in which direction to move by calculating gradients, but when the footstep is going to be too big, you just adjust the size of footstep to the threshold size you have set. In a pseudo code, write a gradient clipping part only with two line code as below.

*\boldsymbol{g} is a gradient at the time step threshold is the maximum size of the “step.”

The figure below, cited from a deep learning text from MIT press textbook, is a good and straightforward explanation on gradient clipping.It is known that a strongly nonlinear function, such as error functions of RNN, can have very steep or plain areas. If you artificially visualize the idea in 3-dimensional space, as the surface of a loss function J with two variants w, b, that means the loss function J has plain areas and very steep cliffs like in the figure.Without gradient clipping, at the left side, you can see that the black dot all of a sudden climb the cliff and could jump to an unexpected area. But with gradient clipping, you avoid such “big jumps” on error functions.

Source: Source: Goodfellow and Yoshua Bengio and Aaron Courville, Deep Learning, (2016), MIT Press, 409p

 

I am glad that I have finally finished this article series. I am not sure how many of the readers would have read through all of the articles in this series, including my PowerPoint slides. I bet that is not so many. I spent a great deal of my time for making these contents, but sadly even when I was studying LSTM, it was becoming old-fashioned, at least in natural language processing (NLP) field: a very promising algorithm named Transformer has been replacing the position of LSTM. Deep learning is a very fast changing field. I also would like to make illustrative introductions on attention mechanism in NLP, from seq2seq model to Transformer. And I think LSTM would still remain as one of the algorithms in sequence data processing, such as hidden Hidden Markov model, or particle filter.

Simple RNN
Yasuto Tamura

Understanding LSTM forward propagation in two ways

/in , , , , , , , /by

*This article is only for the sake of understanding the equations in the second page of the paper named “LSTM: A Search Space Odyssey”. If you have no trouble understanding the equations of LSTM forward propagation, I recommend you to skip this article and go the the next article.

1. Preface

I  heard that in Western culture, smart people write textbooks so that other normal people can understand difficult stuff, and that is why textbooks in Western countries tend to be bulky, but also they are not so difficult as they look. On the other hand in Asian culture, smart people write puzzling texts on esoteric topics, and normal people have to struggle to understand what noble people wanted to say. Publishers also require the authors to keep the texts as short as possible, so even though the textbooks are thin, usually students have to repeat reading the textbooks several times because usually they are too abstract.

Both styles have cons and pros, and usually I prefer Japanese textbooks because they are concise, and sometimes it is annoying to read Western style long texts with concrete straightforward examples to reach one conclusion. But a problem is that when it comes to explaining LSTM, almost all the text books are like Asian style ones. Every study material seems to skip the proper steps necessary for “normal people” to understand its algorithms. But after actually making concrete slides on mathematics on LSTM, I understood why: if you write down all the equations on LSTM forward/back propagation, that is going to be massive, and actually I had to make 100-page PowerPoint animated slides to make it understandable to people like me.

I already had a feeling that “Does it help to understand only LSTM with this precision? I should do more practical codings.” For example François Chollet, the developer of Keras, in his book, said as below.

 

For me that sounds like “We have already implemented RNNs for you, so just shut up and use Tensorflow/Keras.” Indeed, I have never cared about the architecture of my Mac Book Air, but I just use it every day, so I think he is to the point. To make matters worse, for me, a promising algorithm called Transformer seems to be replacing the position of LSTM in natural language processing. But in this article series and in my PowerPoint slides, I tried to explain as much as possible, contrary to his advice.

But I think, or rather hope,  it is still meaningful to understand this 23-year-old algorithm, which is as old as me. I think LSTM did build a generation of algorithms for sequence data, and actually Sepp Hochreiter, the inventor of LSTM, has received Neural Network Pioneer Award 2021 for his work.

I hope those who study sequence data processing in the future would come to this article series, and study basics of RNN just as I also study classical machine learning algorithms.

 *In this article “Densely Connected Layers” is written as “DCL,” and “Convolutional Neural Network” as “CNN.”

2. Why LSTM?

First of all, let’s take a brief look at what I said about the structures of RNNs,  in the first and the second article. A simple RNN is basically densely connected network with a few layers. But the RNN gets an input every time step, and it gives out an output at the time step. Part of information in the middle layer are succeeded to the next time step, and in the next time step, the RNN also gets an input and gives out an output. Therefore, virtually a simple RNN behaves almost the same way as densely connected layers with many layers during forward/back propagation if you focus on its recurrent connections.

That is why simple RNNs suffer from vanishing/exploding gradient problems, where the information exponentially vanishes or explodes when its gradients are multiplied many times through many layers during back propagation. To be exact, I think you need to consider this problem precisely like you can see in this paper. But for now, please at least keep it in mind that when you calculate a gradient of an error function with respect to parameters of simple neural networks, you have to multiply parameters many times like below, and this type of calculation usually leads to vanishing/exploding gradient problem.

LSTM was invented as a way to tackle such problems as I mentioned in the last article.

3. How to display LSTM

I would like you to just go to image search on Google, Bing, or Yahoo!, and type in “LSTM.” I think you will find many figures, but basically LSTM charts are roughly classified into two types: in this article I call them “Space Odyssey type” and “electronic circuit type”, and in conclusion, I highly recommend you to understand LSTM as the “electronic circuit type.”

*I just randomly came up with the terms “Space Odyssey type” and “electronic circuit type” because the former one is used in the paper I mentioned, and the latter one looks like an electronic circuit to me. You do not have to take how I call them seriously.

However, not that all the well-made explanations on LSTM use the “electronic circuit type,” and I am sure you sometimes have to understand LSTM as the “space odyssey type.” And the paper “LSTM: A Search Space Odyssey,” which I learned a lot about LSTM from,  also adopts the “Space Odyssey type.”

LSTM architectur visualization

The main reason why I recommend the “electronic circuit type” is that its behaviors look closer to that of simple RNNs, which you would have seen if you read my former articles.

*Behaviors of both of them look different, but of course they are doing the same things.

If you have some understanding on DCL, I think it was not so hard to understand how simple RNNs work because simple RNNs  are mainly composed of linear connections of neurons and weights, whose structures are the same almost everywhere. And basically they had only straightforward linear connections as you can see below.

But from now on, I would like you to give up the ideas that LSTM is composed of connections of neurons like the head image of this article series. If you do that, I think that would be chaotic and I do not want to make a figure of it on Power Point. In short, sooner or later you have to understand equations of LSTM.

4. Forward propagation of LSTM in “electronic circuit type”

*For further understanding of mathematics of LSTM forward/back propagation, I recommend you to download my slides.

The behaviors of an LSTM block is quite similar to that of a simple RNN block: an RNN block gets an input every time step and gets information from the RNN block of the last time step, via recurrent connections. And the block succeeds information to the next block.

Let’s look at the simplified architecture of  an LSTM block. First of all, you should keep it in mind that LSTM have two streams of information: the one going through all the gates, and the one going through cell connections, the “highway” of LSTM block. For simplicity, we will see the architecture of an LSTM block without peephole connections, the lines in blue. The flow of information through cell connections is relatively uninterrupted. This helps LSTMs to retain information for a long time.

In a LSTM block, the input and the output of the former time step separately go through sections named “gates”: input gate, forget gate, output gate, and block input. The outputs of the forget gate, the input gate, and the block input join the highway of cell connections to renew the value of the cell.

*The small two dots on the cell connections are the “on-ramp” of cell conection highway.

*You would see the terms “input gate,” “forget gate,” “output gate” almost everywhere, but how to call the “block gate” depends on textbooks.

Let’s look at the structure of an LSTM block a bit more concretely. An LSTM block at the time step (t) gets \boldsymbol{y}^{(t-1)}, the output at the last time step,  and \boldsymbol{c}^{(t-1)}, the information of the cell at the time step (t-1), via recurrent connections. The block at time step (t) gets the input \boldsymbol{x}^{(t)}, and it separately goes through each gate, together with \boldsymbol{y}^{(t-1)}. After some calculations and activation, each gate gives out an output. The outputs of the forget gate, the input gate, the block input, and the output gate are respectively \boldsymbol{f}^{(t)}, \boldsymbol{i}^{(t)}, \boldsymbol{z}^{(t)}, \boldsymbol{o}^{(t)}. The outputs of the gates are mixed with \boldsymbol{c}^{(t-1)} and the LSTM block gives out an output \boldsymbol{y}^{(t)}, and gives \boldsymbol{y}^{(t)} and \boldsymbol{c}^{(t)} to the next LSTM block via recurrent connections.

You calculate \boldsymbol{f}^{(t)}, \boldsymbol{i}^{(t)}, \boldsymbol{z}^{(t)}, \boldsymbol{o}^{(t)} as below.

  • \boldsymbol{f}^{(t)}= \sigma(\boldsymbol{W}_{for} \boldsymbol{x}^{(t)} + \boldsymbol{R}_{for} \boldsymbol{y}^{(t-1)} + \boldsymbol{b}_{for})
  • \boldsymbol{i}^{(t)}=\sigma(\boldsymbol{W}_{in} \boldsymbol{x}^{(t)} + \boldsymbol{R}_{in} \boldsymbol{y}^{(t-1)} + \boldsymbol{b}_{in})
  • \boldsymbol{z}^{(t)}=tanh(\boldsymbol{W}_z \boldsymbol{x}^{(t)} + \boldsymbol{R}_z \boldsymbol{y}^{(t-1)} + \boldsymbol{b}_z)
  • \boldsymbol{o}^{(t)}=\sigma(\boldsymbol{W}_{out} \boldsymbol{x}^{(t)} + \boldsymbol{R}_{out} \boldsymbol{y}^{(t-1)} + \boldsymbol{b}_{out})

*You have to keep it in mind that the equations above do not include peephole connections, which I am going to show with blue lines in the end.

The equations above are quite straightforward if you understand forward propagation of simple neural networks. You add linear products of \boldsymbol{y}^{(t)} and \boldsymbol{c}^{(t)} with different weights in each gate. What makes LSTMs different from simple RNNs is how to mix the outputs of the gates with the cell connections. In order to explain that, I need to introduce a mathematical operator called Hadamard product, which you denote as \odot. This is a very simple operator. This operator produces an elementwise product of two vectors or matrices with identical shape.

With this Hadamar product operator, the renewed cell and the output are calculated as below.

  • \boldsymbol{c}^{(t)} = \boldsymbol{z}^{(t)}\odot \boldsymbol{i}^{(t)} + \boldsymbol{c}^{(t-1)} \odot \boldsymbol{f}^{(t)}
  • \boldsymbol{y}^{(t)} = \boldsymbol{o}^{(t)} \odot tanh(\boldsymbol{c}^{(t)})

The values of \boldsymbol{f}^{(t)}, \boldsymbol{i}^{(t)}, \boldsymbol{z}^{(t)}, \boldsymbol{o}^{(t)} are compressed into the range of [0, 1] or [-1, 1] with activation functions. You can see that the input gate and the block input give new information to the cell. The part \boldsymbol{c}^{(t-1)} \odot \boldsymbol{f}^{(t)} means that the output of the forget gate “forgets” the cell of the last time step by multiplying the values from 0 to 1 elementwise. And the cell \boldsymbol{c}^{(t)} is activated with tanh() and the output of the output gate “suppress” the activated value of \boldsymbol{c}^{(t)}. In other words, the output gatedecides how much information to give out as an output of the LSTM block. The output of every gate depends on the input \boldsymbol{x}^{(t)}, and the recurrent connection \boldsymbol{y}^{(t-1)}. That means an LSTM block learns to forget the cell of the last time step, to renew the cell, and to suppress the output. To describe in an extreme manner, if all the outputs of every gate are always (1, 1, …1)^T, LSTMs forget nothing, retain information of inputs at every time step, and gives out everything. And  if all the outputs of every gate are always (0, 0, …0)^T, LSTMs forget everything, receive no inputs, and give out nothing.

This model has one problem: the outputs of each gate do not directly depend on the information in the cell. To solve this problem, some LSTM models introduce some flows of information from the cell to each gate, which are shown as lines in blue in the figure below.

LSTM inner architecture

LSTM models, for example the one with or without peephole connection, depend on the library you use, and the model I have showed is one of standard LSTM structure. However no matter how complicated structure of an LSTM block looks, you usually cover it with a black box as below and show its behavior in a very simplified way.

5. Space Odyssey type

I personally think there is no advantages of understanding how LSTMs work with this Space Odyssey type chart, but in several cases you would have to use this type of chart. So I will briefly explain how to look at that type of chart, based on understandings of LSTMs you have gained through this article.

In Space Odyssey type of LSTM chart, at the center is a cell. Electronic circuit type of chart, which shows the flow of information of the cell as an uninterrupted “highway” in an LSTM block. On the other hand, in a Spacey Odyssey type of chart, the information of the cell rotate at the center. And each gate gets the information of the cell through peephole connections,  \boldsymbol{x}^{(t)}, the input at the time step (t) , sand \boldsymbol{y}^{(t-1)}, the output at the last time step (t-1), which came through recurrent connections. In Space Odyssey type of chart, you can more clearly see that the information of the cell go to each gate through the peephole connections in blue. Each gate calculates its output.

Just as the charts you have seen, the dotted line denote the information from the past. First, the information of the cell at the time step (t-1) goes to the forget gate and get mixed with the output of the forget cell In this process the cell is partly “forgotten.” Next, the input gate and the block input are mixed to generate part of new value of the the cell at time step  (t). And the partly “forgotten” \boldsymbol{c}^{(t-1)} goes back to the center of the block and it is mixed with the output of the input gate and the block input. That is how \boldsymbol{c}^{(t)} is renewed. And the value of new cell flow to the top of the chart, being mixed with the output of the output gate. Or you can also say the information of new cell is “suppressed” with the output gate.

I have finished the first four articles of this article series, and finally I am gong to write about back propagation of LSTM in the next article. I have to say what I have written so far is all for the next article, and my long long Power Point slides.

 

[References]

[1] Klaus Greff, Rupesh Kumar Srivastava, Jan Koutník, Bas R. Steunebrink, Jürgen Schmidhuber, “LSTM: A Search Space Odyssey,” (2017)

[2] Francois Chollet, Deep Learning with Python,(2018), Manning , pp. 202-204

[3] “Sepp Hochreiter receives IEEE CIS Neural Networks Pioneer Award 2021”, Institute of advanced research in artificial intelligence, (2020)
URL: https://www.iarai.ac.at/news/sepp-hochreiter-receives-ieee-cis-neural-networks-pioneer-award-2021/?fbclid=IwAR27cwT5MfCw4Tqzs3MX_W9eahYDcIFuoGymATDR1A-gbtVmDpb8ExfQ87A

[4] Oketani Takayuki, “Machine Learning Professional Series: Deep Learning,” (2015), pp. 120-125
岡谷貴之 著, 「機械学習プロフェッショナルシリーズ 深層学習」, (2015), pp. 120-125

[5] Harada Tatsuya, “Machine Learning Professional Series: Image Recognition,” (2017), pp. 252-257
原田達也 著, 「機械学習プロフェッショナルシリーズ 画像認識」, (2017), pp. 252-257

[6] “Understandable LSTM ~ With the Current Trends,” Qiita, (2015)
「わかるLSTM ～ 最近の動向と共に」, Qiita, (2015)
URL: https://qiita.com/t_Signull/items/21b82be280b46f467d1b

Simple RNN
Yasuto Tamura

Prerequisites for understanding RNN at a more mathematical level

/in , , , , , , , , , , /by

Writing the A gentle introduction to the tiresome part of understanding RNN Article Series on recurrent neural network (RNN) is nothing like a creative or ingenious idea. It is quite an ordinary topic. But still I am going to write my own new article on this ordinary topic because I have been frustrated by lack of sufficient explanations on RNN for slow learners like me.

I think many of readers of articles on this website at least know that RNN is a type of neural network used for AI tasks, such as time series prediction, machine translation, and voice recognition. But if you do not understand how RNNs work, especially during its back propagation, this blog series is for you.

After reading this articles series, I think you will be able to understand RNN in more mathematical and abstract ways. But in case some of the readers are allergic or intolerant to mathematics, I tried to use as little mathematics as possible.

Ideal prerequisite knowledge:

  • Some understanding on densely connected layers (or fully connected layers, multilayer perception) and how their forward/back propagation work.
  •  Some understanding on structure of Convolutional Neural Network.

*In this article “Densely Connected Layers” is written as “DCL,” and “Convolutional Neural Network” as “CNN.”

1, Difficulty of Understanding RNN

I bet a part of difficulty of understanding RNN comes from the variety of its structures. If you search “recurrent neural network” on Google Image or something, you will see what I mean. But that cannot be helped because RNN enables a variety of tasks.

Another major difficulty of understanding RNN is understanding its back propagation algorithm. I think some of you found it hard to understand chain rules in calculating back propagation of densely connected layers, where you have to make the most of linear algebra. And I have to say backprop of RNN, especially LSTM, is a monster of chain rules. I am planing to upload not only a blog post on RNN backprop, but also a presentation slides with animations to make it more understandable, in some external links.

In order to avoid such confusions, I am going to introduce a very simplified type of RNN, which I call a “simple RNN.” The RNN displayed as the head image of this article is a simple RNN.

2, How Neurons are Connected

    \begin{equation*} 1 = 3 - 2 \end{equation*}

How to connect neurons and how to activate them is what neural networks are all about. Structures of those neurons are easy to grasp as long as that is about DCL or CNN. But when it comes to the structure of RNN, many study materials try to avoid showing that RNNs are also connections of neurons, as well as DCL or CNN(*If you are not sure how neurons are connected in CNN, this link should be helpful. Draw a random digit in the square at the corner.). In fact the structure of RNN is also the same, and as long as it is a simple RNN, and it is not hard to visualize its structure.

Even though RNN is also connections of neurons, usually most RNN charts are simplified, using blackboxes. In case of simple RNN, most study material would display it as the chart below.

But that also cannot be helped because fancier RNN have more complicated connections of neurons, and there are no longer advantages of displaying RNN as connections of neurons, and you would need to understand RNN in more abstract way, I mean, as you see in most of textbooks.

I am going to explain details of simple RNN in the next article of this series.

3, Neural Networks as Mappings

If you still think that neural networks are something like magical spider webs or models of brain tissues, forget that. They are just ordinary mappings.

If you have been allergic to mathematics in your life, you might have never heard of the word “mapping.” If so, at least please keep it in mind that the equation y=f(x), which most people would have seen in compulsory education, is a part of mapping. If you get a value x, you get a value y corresponding to the x.

But in case of deep learning, x is a vector or a tensor, and it is denoted with \boldsymbol{x} . If you have never studied linear algebra , imagine that a vector is a column of Excel data (only one column), a matrix is a sheet of Excel data (with some rows and columns), and a tensor is some sheets of Excel data (each sheet does not necessarily contain only one column.)

CNNs are mainly used for image processing, so their inputs are usually image data. Image data are in many cases (3, hight, width) tensors because usually an image has red, blue, green channels, and the image in each channel can be expressed as a hight*width matrix (the “height” and the “width” are number of pixels, so they are discrete numbers).

The convolutional part of CNN (which I call “feature extraction part”) maps the tensors to a vector, and the last part is usually DCL, which works as classifier/regressor. At the end of the feature extraction part, you get a vector. I call it a “semantic vector” because the vector has information of “meaning” of the input image. In this link you can see maps of pictures plotted depending on the semantic vector. You can see that even if the pictures are not necessarily close pixelwise, they are close in terms of the “meanings” of the images.

In the example of a dog/cat classifier introduced by François Chollet, the developer of Keras, the CNN maps (3, 150, 150) tensors to 2-dimensional vectors, (1, 0) or (0, 1) for (dog, cat).

Wrapping up the points above, at least you should keep two points in mind: first, DCL is a classifier or a regressor, and CNN is a feature extractor used for image processing. And another important thing is, feature extraction parts of CNNs map images to vectors which are more related to the “meaning” of the image.

Importantly, I would like you to understand RNN this way. An RNN is also just a mapping.

*I recommend you to at least take a look at the beautiful pictures in this link. These pictures give you some insight into how CNN perceive images.

4, Problems of DCL and CNN, and needs for RNN

Taking an example of RNN task should be helpful for this topic. Probably machine translation is the most famous application of RNN, and it is also a good example of showing why DCL and CNN are not proper for some tasks. Its algorithms is out of the scope of this article series, but it would give you a good insight of some features of RNN. I prepared three sentences in German, English, and Japanese, which have the same meaning. Assume that each sentence is divided into some parts as shown below and that each vector corresponds to each part. In machine translation we want to convert a set of the vectors into another set of vectors.

Then let’s see why DCL and CNN are not proper for such task.

  • The input size is fixed: In case of the dog/cat classifier I have mentioned, even though the sizes of the input images varies, they were first molded into (3, 150, 150) tensors. But in machine translation, usually the length of the input is supposed to be flexible.
  • The order of inputs does not mater: In case of the dog/cat classifier the last section, even if the input is “cat,” “cat,” “dog” or “dog,” “cat,” “cat” there’s no difference. And in case of DCL, the network is symmetric, so even if you shuffle inputs, as long as you shuffle all of the input data in the same way, the DCL give out the same outcome . And if you have learned at least one foreign language, it is easy to imagine that the orders of vectors in sequence data matter in machine translation.

*It is said English language has phrase structure grammar, on the other hand Japanese language has dependency grammar. In English, the orders of words are important, but in Japanese as long as the particles and conjugations are correct, the orders of words are very flexible. In my impression, German grammar is between them. As long as you put the verb at the second position and the cases of the words are correct, the orders are also relatively flexible.

5, Sequence Data

We can say DCL and CNN are not useful when you want to process sequence data. Sequence data are a type of data which are lists of vectors. And importantly, the orders of the vectors matter. The number of vectors in sequence data is usually called time steps. A simple example of sequence data is meteorological data measured at a spot every ten minutes, for instance temperature, air pressure, wind velocity, humidity. In this case the data is recorded as 4-dimensional vector every ten minutes.

But this “time step” does not necessarily mean “time.” In case of natural language processing (including machine translation), which you I mentioned in the last section, the numberings of each vector denoting each part of sentences are “time steps.”

And RNNs are mappings from a sequence data to another sequence data.

*At least I found a paper on the RNN’s capability of universal approximation on many-to-one RNN task. But I have not found any papers on universal approximation of many-to-many RNN tasks. Please let me know if you find any clue on whether such approximation is possible. I am desperate to know that. 

6, Types of RNN Tasks

RNN tasks can be classified into some types depending on the lengths of input/output sequences (the “length” means the times steps of input/output sequence data).

If you want to predict the temperature in 24 hours, based on several time series data points in the last 96 hours, the task is many-to-one. If you sample data every ten minutes, the input size is 96*6=574 (the input data is a list of 574 vectors), and the output size is 1 (which is a value of temperature). Another example of many-to-one task is sentiment classification. If you want to judge whether a post on SNS is positive or negative, the input size is very flexible (the length of the post varies.) But the output size is one, which is (1, 0) or (0, 1), which denotes (positive, negative).

*The charts in this section are simplified model of RNN used for each task. Please keep it in mind that they are not 100% correct, but I tried to make them as exact as possible compared to those in other study materials.

Music/text generation can be one-to-many tasks. If you give the first sound/word you can generate a phrase.

Next, let’s look at many-to-many tasks. Machine translation and voice recognition are likely to be major examples of many-to-many tasks, but here name entity recognition seems to be a proper choice. Name entity recognition is task of finding proper noun in a sentence . For example if you got two sentences “He said, ‘Teddy bears on sale!’ ” and ‘He said, “Teddy Roosevelt was a great president!” ‘ judging whether the “Teddy” is a proper noun or a normal noun is name entity recognition.

Machine translation and voice recognition, which are more popular, are also many-to-many tasks, but they use more sophisticated models. In case of machine translation, the inputs are sentences in the original language, and the outputs are sentences in another language. When it comes to voice recognition, the input is data of air pressure at several time steps, and the output is the recognized word or sentence. Again, these are out of the scope of this article but I would like to introduce the models briefly.

Machine translation uses a type of RNN named sequence-to-sequence model (which is often called seq2seq model). This model is also very important for other natural language processes tasks in general, such as text summarization. A seq2seq model is divided into the encoder part and the decoder part. The encoder gives out a hidden state vector and it used as the input of the decoder part. And decoder part generates texts, using the output of the last time step as the input of next time step.

Voice recognition is also a famous application of RNN, but it also needs a special type of RNN.

*To be honest, I don’t know what is the state-of-the-art voice recognition algorithm. The example in this article is a combination of RNN and a collapsing function made using Connectionist Temporal Classification (CTC). In this model, the output of RNN is much longer than the recorded words or sentences, so a collapsing function reduces the output into next output with normal length.

You might have noticed that RNNs in the charts above are connected in both directions. Depending on the RNN tasks you need such bidirectional RNNs.  I think it is also easy to imagine that such networks are necessary. Again, machine translation is a good example.

And interestingly, image captioning, which enables a computer to describe a picture, is one-to-many-task. As the output is a sentence, it is easy to imagine that the output is “many.” If it is a one-to-many task, the input is supposed to be a vector.

Where does the input come from? I told you that I was obsessed with the beauty of the last vector of the feature extraction part of CNN. Surprisingly the the “beautiful” vector, which I call a “semantic vector” is the input of image captioning task (after some transformations, depending on the network models).

I think this articles includes major things you need to know as prerequisites when you want to understand RNN at more mathematical level. In the next article, I would like to explain the structure of a simple RNN, and how it forward propagate.

* I make study materials on machine learning, sponsored by DATANOMIQ. I do my best to make my content as straightforward but as precise as possible. I include all of my reference sources. If you notice any mistakes in my materials, please let me know (email: yasuto.tamura@datanomiq.de). And if you have any advice for making my materials more understandable to learners, I would appreciate hearing it.

Michael Lyamm

Closing the AI-skills gap with Upskilling

/in , /by

Closing the AI-skills gap with Upskilling

Artificial Intelligent or as it is fancily referred as AI, has garnered huge popularity worldwide.  And given the career prospects it has, it definitely should. Almost everyone interested in technology sector has them rushing towards it, especially young and motivated fresh computer science graduates. Compared to other IT-related jobs AI pays way higher salary and have opportunities. According to a Glassdoor report, Data Scientist, one of the many related jobs, is the number one job with good salary, job openings and more. AI-related jobs include Data Scientists, Analysts, Machine Learning Engineer, NLP experts etc.

AI has found applications in almost every industry and thus it has picked up demand. Home assistants – Siri, Ok Google, Amazon Echo — chatbots, and more some of the popular applications of AI.

Increasing adoption of AI across Industry

The advantages of AI like increased productivity has increased its adoption among companies. According to Gartner, 37 percent of enterprise currently use AI in one way or the other. In fact, in the last four year adoption of AI technologies among companies has increased by 270 percent. In telecommunications, for instance, 52 percent of companies have chatbots deployed for better and smoother customer experience. Now, about 49 percent of businesses are now on their way to alter business models to integrate and adopt AI-driven processes. Further, industry leaders have gone beyond and voiced their concerns about companies that are lagging in AI adoption.

Unfortunately, it has been extremely difficult for employers to find right skilled or qualified candidates for AI-related positions. A reports suggests that there are total 300,000 AI professionals are available worldwide, while there’s demand for millions. In a recent survey conducted by Ernst & Young, 51 percent AI professionals told that lack of talent was the biggest impediment in AI adoption.

Further, O’Reilly, in 2018 conducted a survey, which found the lack of AI skills, among other things, was the major reason that was holding companies back from implementing AI.
The major reason for this is the lack of skills among people who aspire to get into AI-related jobs. According to a report, there demand for millions for jobs in AI. However, only a handful of qualified people are available.

Bridging the skill gap in AI-related jobs

Top companies and government around the world have taken up initiatives to close this gap. Google and Amazon, for instance, have dedicated facilities which trains in AI skills.  Google’s Brain Toronto is a dedicated facility to expand their talent in AI.  Similarly, Amazon has facility near University of Cambridge which is dedicated to AI. Most companies either already have a facility or are in the process of setting up one.

In addition to this, governments around the world are also taking initiatives to address the skill gap. For instance, government across the world are pushing towards AI advancement and are develop collaborative plans which aims at delivering more AI skilled professionals. Recently, the white house launched ai.gov which is further helping to promote AI in the US. The website will offer updates related to AI projects across different sectors.

Other than these, companies have taken this upon themselves to reskills their employees and prepare them for future roles. According to a report from Towards Data Science, about 63 percent of companies have in-house training programs to train employees in AI-related skills.

Overall, though there is demand for AI professionals, lack of skilled talent is a major problem.

Roles in Artificial Intelligence
Artificial Intelligence is the most dominant role for which companies hire across artificial Intelligence. Other than that, following are some of the popular roles:

  1. Machine learning Engineer: These are the people who make machines learn with complex algorithms. On advance level, Machine learning engineers are required to have good knowledge of computer vision. According to Indeed, in the last year, demand for Machine Learning Engineer has grown by 344 percent.
  2. NLP Experts: These experts are equipped with the understanding of making machines computer understand human language. Their expertise includes knowledge of how machines understand human language. Text-to-speech technologies are the common areas which require NLP experts. Demand for engineers who can program computers to understand human speech is growing continuously. It was the fast growing skills in Upwork’s list of in-demand freelancing skills. In Q4, 2016, it had grown 200 percent and since then has been on continuously growing.
  3. Big Data Engineers: This is majorly an analytics role. These gather huge amount of data available from sources and analyze it to derive insights and understand patter, which may be further used for machine learning, prediction modelling, natural language processing. In Mckinsey annual report 2018, it had reported that there was shortage of 190,000 big data professionals in the US alone.

Other roles like Data Scientists, Analysts, and more also in great demand. Then, again due to insufficient talent in the market, companies are struggling to hire for these roles.

Self-learning and upskilling
Artificial Intelligence is a continuously growing field and it has been advancing at a very fast pace, and it makes extremely difficult to keep up with in-demand skills. Hence, it is imperative to keep yourself up with demand of the industry, or it is just a matter of time before one becomes redundant.

On an individual level, learning new skills is necessary. One has to be agile and keep learning, and be ready to adapt new technologies. For this, AI training programs and certifications are ideal.  There are numerous AI programs which individuals can take to further learn new skills. AI certifications can immensely boost career opportunities. Certification programs offer a structured approach to learning which benefits in learning mostly practical and executional skills while keeping fluff away. It is more hands-on. Plus, certifications programs qualify only when one has passed practical test which is very advantageous in tech. AI certifications like AIE (Artificial Intelligence Engineer) are quite popular.

Online learning platforms also offer good a resource to learn artificial intelligence. Most schools haven’t yet adapted their curriculum to skill for AI, while most universities and grad schools are in their way to do so. In the meantime, online learning platforms offer a good way to learn AI skills, where one can start from basic and reach to advance skills.